差分--差分数组快速计算L到R值相加后的数组
目录
- 差分:
- 思路
- 代码:
原题链接
差分:
输入一个长度为 n
的整数序列。
接下来输入 m
个操作,每个操作包含三个整数 l,r,c
,表示将序列中 [l,r]
之间的每个数加上 c
。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数 n
和 m
。
第二行包含 n
个整数,表示整数序列。
接下来 m
行,每行包含三个整数 l,r,c
,表示一个操作。
输出格式
共一行,包含 n
个整数,表示最终序列。
数据范围
1≤n,m≤100000
,
1≤l≤r≤n
,
−1000≤c≤1000
,
−1000≤整数序列中元素的值≤1000
输入样例:
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例:
3 4 5 3 4 2
思路
这题按照常规的思路 那就是用for循环l到r直接到数字 时间复杂度比较高
差分
类似于数学中的求导和积分,差分可以看成前缀和的逆运算。
差分数组:
首先给定一个原数组a:a[1], a[2], a[3], a[n];
然后我们构造一个数组b : b[1] ,b[2] , b[3], b[i];
使得 a[i] = b[1] + b[2 ]+ b[3] +, + b[i]
也就是说,a数组是b数组的前缀和数组,反过来我们把b数组叫做a数组的差分数组。换句话说,每一个a[i]都是b数组中从头开始的一段区间和。
考虑如何构造差分b数组?
最为直接的方法
如下:
a[0 ]= 0;
b[1] = a[1] - a[0];
b[2] = a[2] - a[1];
b[3] =a [3] - a[2];
…
b[n] = a[n] - a[n-1];
图示:
我们只要有b数组,通过前缀和运算,就可以在O(n) 的时间内得到a数组 。
知道了差分数组有什么用呢? 别着急,慢慢往下看。
话说有这么一个问题:
给定区间[l ,r ],让我们把a数组中的[ l, r]区间中的每一个数都加上c,即 a[l] + c , a[l+1] + c , a[l+2] + c , a[r] + c;
暴力做法是for循环l到r区间,时间复杂度O(n),如果我们需要对原数组执行m次这样的操作,时间复杂度就会变成O(n*m)。有没有更高效的做法吗? 考虑差分做法。
始终要记得,a数组是b数组的前缀和数组,比如对b数组的b[i]的修改,会影响到a数组中从a[i]及往后的每一个数。
首先让差分b数组中的 b[l] + c ,a数组变成 a[l] + c ,a[l+1] + c, a[n] + c;
然后我们打个补丁,b[r+1] - c, a数组变成 a[r+1] - c,a[r+2] - c,a[n] - c;
为啥还要打个补丁?
因为原来将b[l]+c后 其l后面的每一个数字都会被影响 ,将b[r+1]-c后 r+1后面的数字的影响又被修改了回来
那么等于只有l到r的这一段区间内的值被影响
代码:
#include<iostream>using namespace std;const int N=1e5+10;int a[N],b[N];
int main()
{int m=0,n=0;cin>>m>>n;for(int i=1;i<=m ;i++){scanf("%d",&a[i]);b[i] = a[i]-a[i-1];}//只修改差分数组里面的值即可while(n--){int l=0,r=0;int val=0;cin>>l>>r>>val;b[l] +=val;b[r+1] -=val;}//将差分数组里面的值同步到a数组里面去for(int i=1;i<=m ;i++){a[i] =a[i-1]+b[i];printf("%d ",a[i]);}return 0;}
相关文章:

差分--差分数组快速计算L到R值相加后的数组
目录 差分:思路代码: 原题链接 差分: 输入一个长度为 n 的整数序列。 接下来输入 m 个操作,每个操作包含三个整数 l,r,c ,表示将序列中 [l,r] 之间的每个数加上 c 。 请你输出进行完所有操作后的序列。 输入格式 第…...
《NLP入门到精通》栏目导读(01/2)
一、说明 栏目《NLP入门到精通》本着从简到难得台阶式学习过度。将自然语言处理得知识贯穿过来。本栏目得前导栏目是《深度学习》、《pytorch实践》,因此,读者需要一定得深度学习基础,才能过度到此栏目内容。 二、博客建设理念 本博客基地,将建成人工智能领域的参考资料库;…...

three.js实现电子围栏效果(纹理贴图)
three.js实现电子围栏效果(纹理贴图) 实现步骤 围栏的坐标坐标转换为几何体顶点,uv顶点坐标加载贴图,移动 图例 代码 <template><div class"app"><div ref"canvesRef" class"canvas-…...
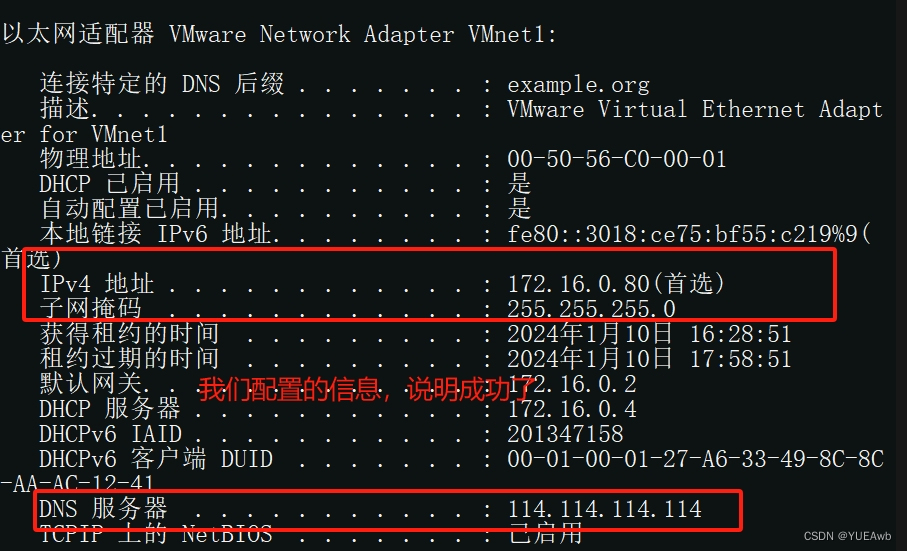
DHSP和DNS
一、服务程序 1.1DHCP定义 DHCP(动态主机配置协议)是一个局域网的网络协议。指的是由服务器控制一段IP地址范围,客户机登录服务器时就可以自动获得服务器分配的IP地址和子网掩码。默认情况下,DHCP作为Windows Server的一个服务组…...

Python冒号的解释
1. “没什么首次没有为第二个,跳了三个”。它得到的切片序列的每一个第三个项目。 扩展片是你想要的。新在Python 2.3 2. Python的序列切片地址可以写成[开始:结束:一步]和任何启动,停止或结束可以被丢弃。a[::3]是每第三个序列。…...
uniapp微信小程序投票系统实战 (SpringBoot2+vue3.2+element plus ) -后端鉴权拦截器实现
锋哥原创的uniapp微信小程序投票系统实战: uniapp微信小程序投票系统实战课程 (SpringBoot2vue3.2element plus ) ( 火爆连载更新中... )_哔哩哔哩_bilibiliuniapp微信小程序投票系统实战课程 (SpringBoot2vue3.2element plus ) ( 火爆连载更新中... )共计21条视频…...

固乔快递查询助手:批量、快速、全面的快递信息查询软件
在快递行业飞速发展的今天,如何高效、准确地掌握快递信息成为了很多人的需求。而固乔快递查询助手正是解决这一难题的利器。 固乔快递查询助手是一款专注于快递信息查询的软件,支持多家主流快递公司查询。用户只需输入单号,即可快速查询到实时…...
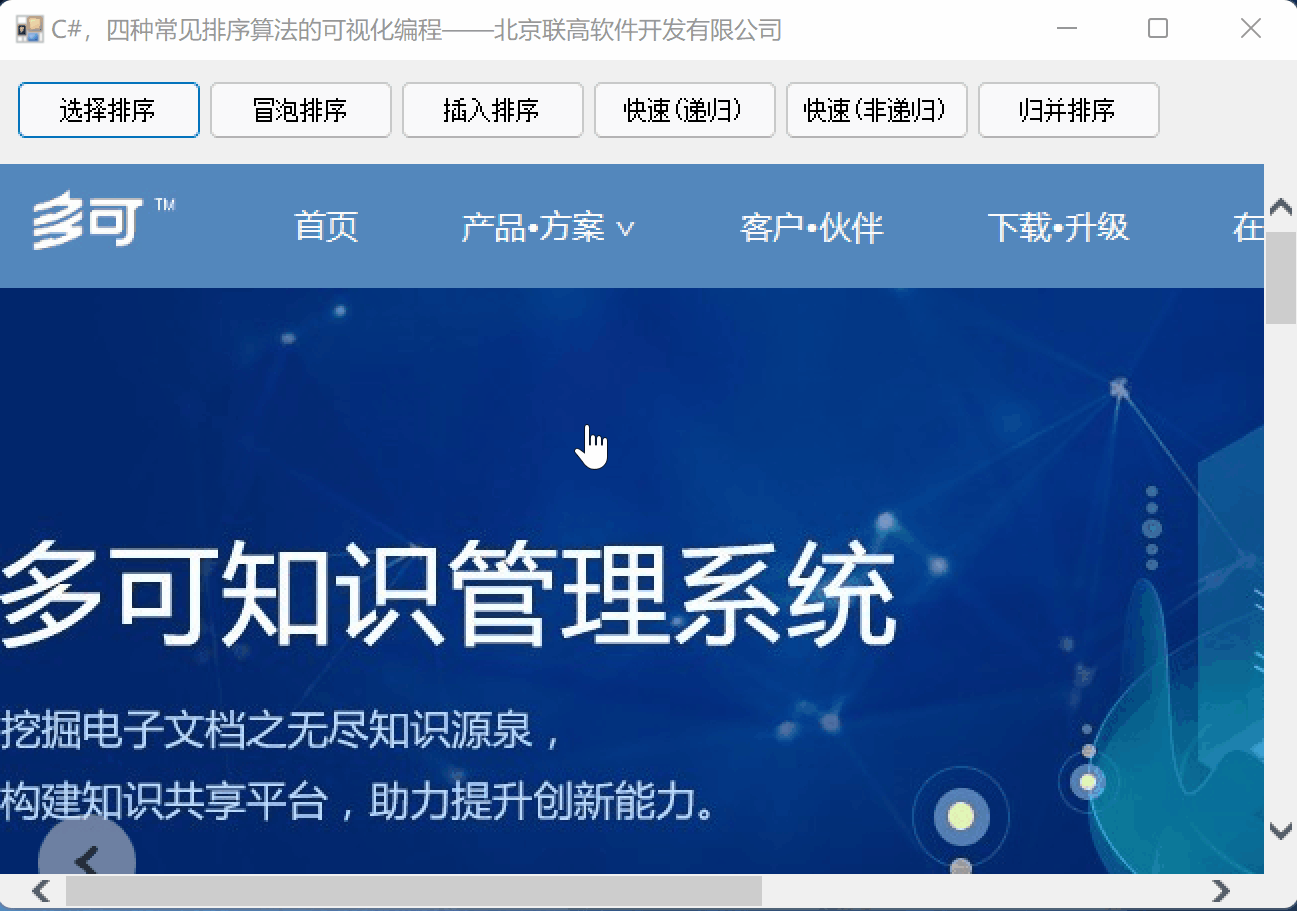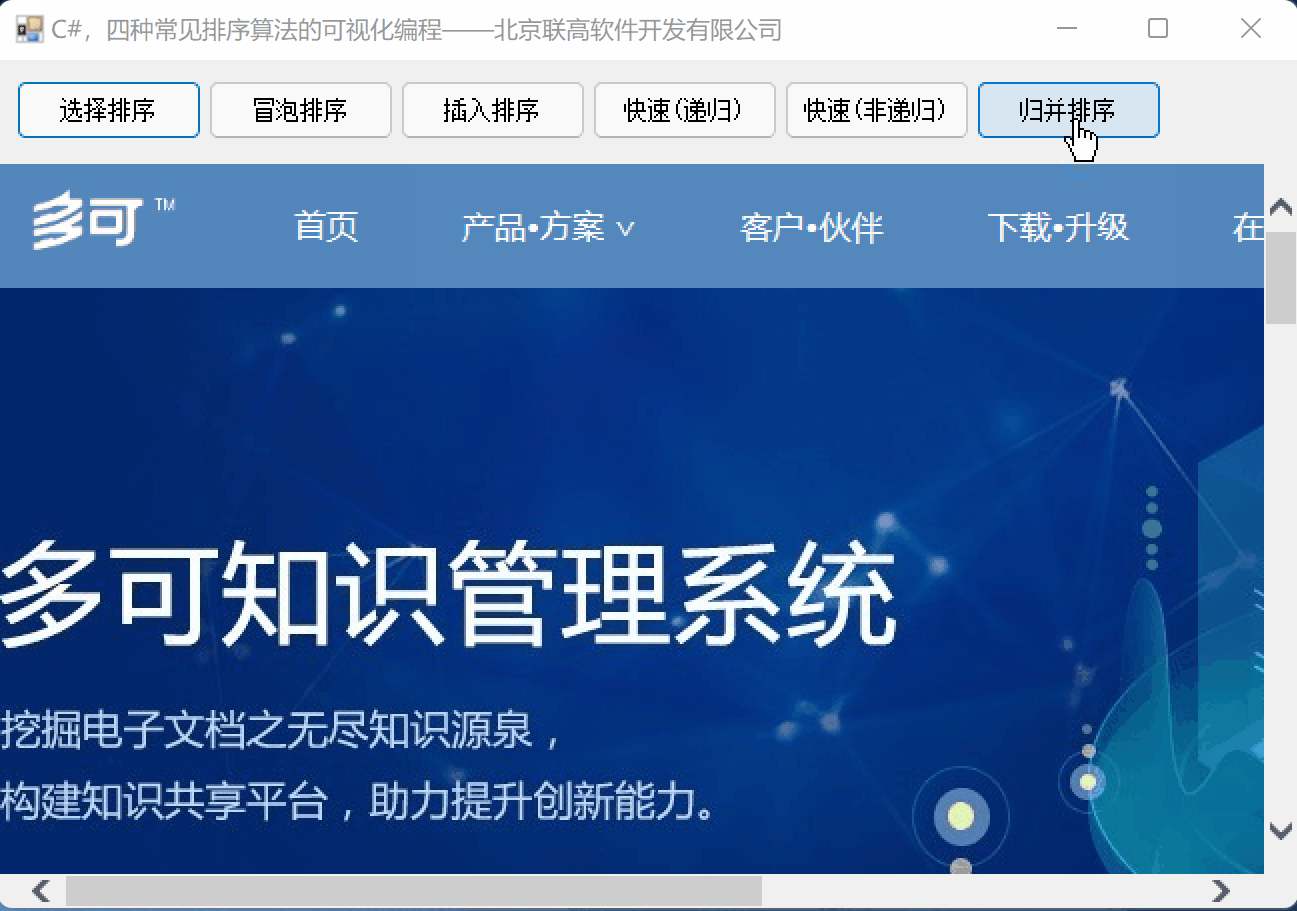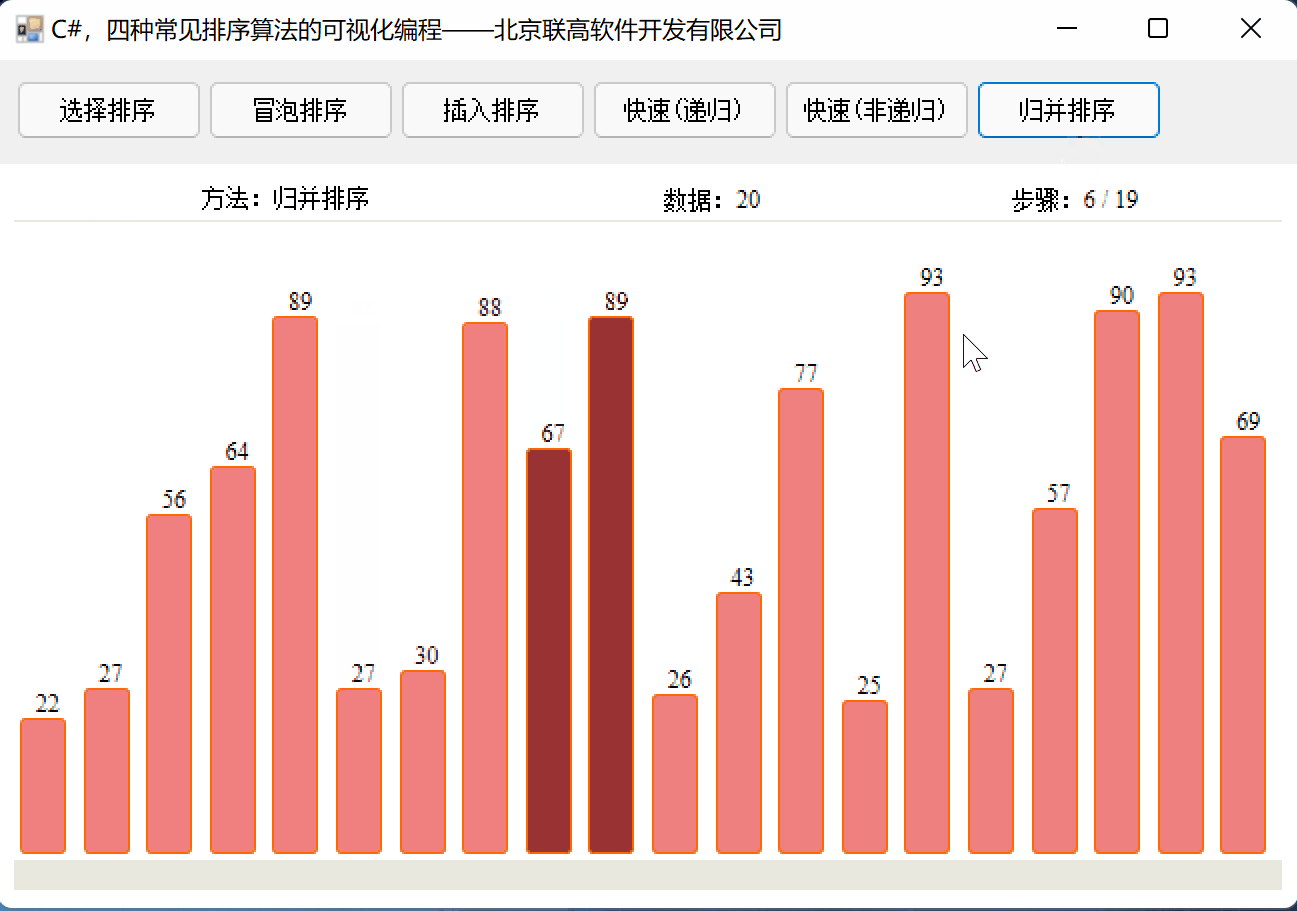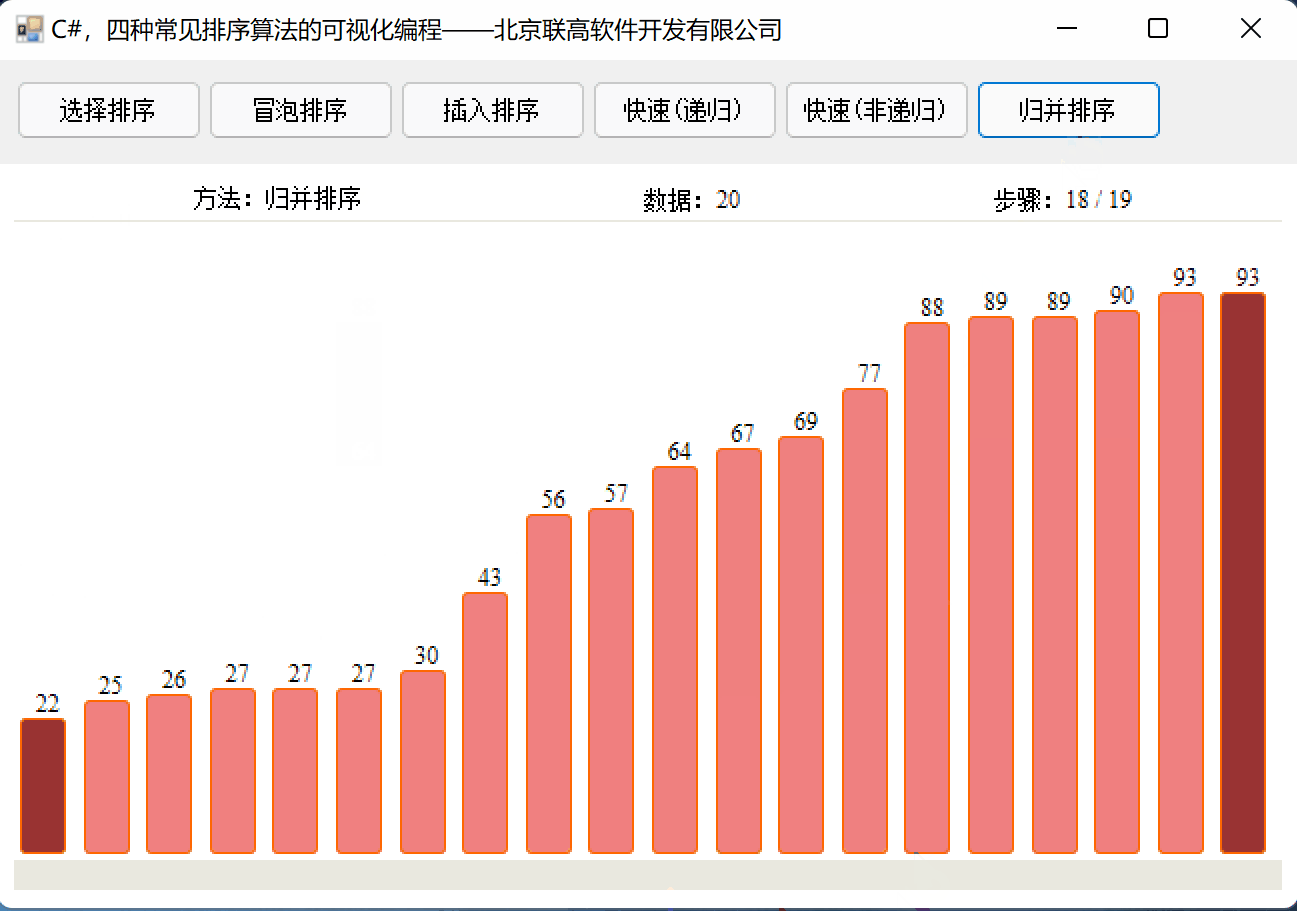
C#,归并排序算法(Merge Sort Algorithm)的源代码及数据可视化
归并排序 归并算法采用非常经典的分治策略,每次把序列分成n/2的长度,将问题分解成小问题,由复杂变简单。 因为使用了递归算法,不能用于大数据的排序。 核心代码: using System; using System.Text; using System.Co…...

Linux的网络服务DHCP
一.了解DHCP服务 1.1 DHCP定义 DHCP(动态主机配置协议)是一个局域网的网络协议。指的是由服务器控制一段IP地址范围,客户机登录服务器时就可以自动获得服务器分配的IP地址和子网掩码。默认情况下,DHCP作为Windows Server的一个服…...
【小沐学CAD】开源Assimp库导入三维模型(C++、Python)
文章目录 1、简介2、下载编译3、代码测试3.1 C3.2 pyassimp(Python) 结语 1、简介 https://github.com/assimp/assimp Open Asset Import Library 是一个库,用于将各种 3D 文件格式加载为共享的内存格式。它支持 40 多种用于导入的文件格式和…...
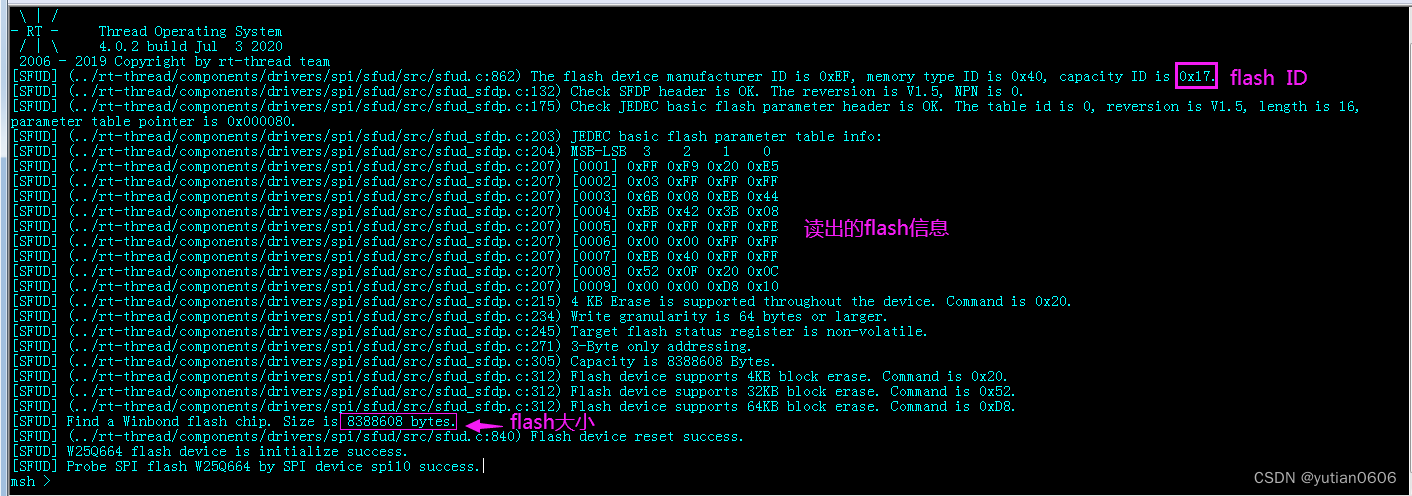
RT-Thread:SPI万能驱动 SFUD 驱动Flash W25Q64,通过 STM32CubeMX 配置 STM32 SPI 驱动
关键词:SFUD,FLASH,W25Q64,W25Q128,STM32F407 说明:RT-Thread 系统 使用 SPI万能驱动 SFUD 驱动 Flash W25Q64,通过 STM32CubeMX 配置 STM32 SPI 驱动。 提示:SFUD添加后的存储位置 1.打开RT-Thread Sett…...
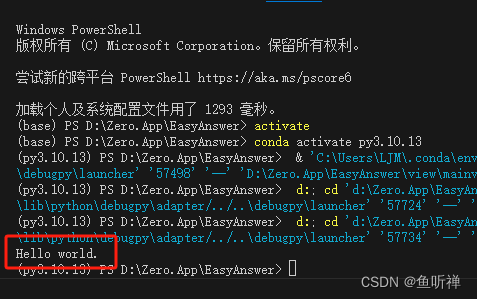
Python学习笔记-使用Anaconda+VSCode配置开发环境
文章目录 概述一、安装Anaconda1.1 下载软件1.2 安装anaconda1.3 配置环境 二、配置虚拟环境2.1 使用conda创建一个新的虚拟环境2.1.1 使用search指令查看支持的python的版本:2.1.2 使用create创建指定版本的虚拟环境:2.1.3 使用env list查看虚拟环境列表…...

RabbitMQ的关键概念解析
RabbitMQ 是一个广泛使用的开源消息代理,它允许应用程序通过复杂的路由和存储机制来交换数据。理解 RabbitMQ 的核心概念对于有效地使用它至关重要。以下是 RabbitMQ 的一些关键概念及其工作流程: 关键概念 生产者(Producer) 生产…...

Python快速排序
快速排序是一种常用的排序算法,它通过递归地将数组分割成较小的子数组,然后对这些子数组进行排序,最终将它们合并成一个有序的数组。具体步骤如下: 1. 选择一个基准元素,通常是数组中的第一个元素。 2. 将数组分成两部…...
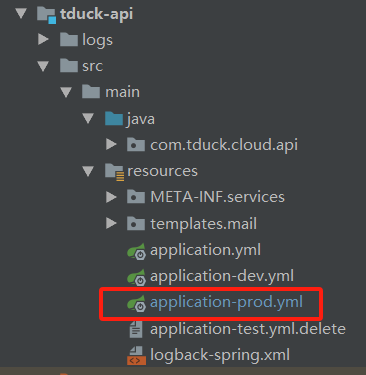
SpringBoot整合人大金仓数据库KingBase
1 去KingBase官网下载驱动jar包 2 将解压得到的所有jar包放置在libs目录下(没有就新建一个目录) 3 在pom文件添加相关依赖 <!--添加KingBase所需要的依赖--> <dependency><groupId>com.kingbase</groupId><artifactId>kin…...

Phoenix基本使用
1、Phoenix简介 1.1 Phoenix定义 Phoenix是HBase的开源SQL皮肤。可以使用标准JDBC API代替HBase客户端API来创建表,插入数据和查询HBase数据。 1.2 Phoenix特点 容易集成:如Spark,Hive,Pig,Flume和Map Reduce。性能…...

31-35.玩转Linux操作系统
玩转Linux操作系统 说明:本文中对Linux命令的讲解都是基于名为CentOS的Linux发行版本,我自己使用的是阿里云服务器,系统版本为CentOS Linux release 7.6.1810。不同的Linux发行版本在Shell命令和工具程序上会有一些差别,但是这些差…...
windows下载官方正版notepad++
一、前言 notepad是一款非常好用的编辑器,简洁、快速、高效。可是很多时候我们想去官网下载时,百度出来的都是一堆第三方下载地址,捆绑流氓软件,要么就是付费,作为一款优秀开源软件,我们必须要知道正确的下…...

Jmeter+ant+jenkins持续集成
一、环境准备 1、 jdk环境 要求JDK1.8以上,命令行输入:java -version,出现如下提示说明安装成功。 2、 Jmeter环境 下载Jmeter最新版本,解压即可,添加bin目录到环境变量。 3、 Ant环境 设置ant环境变量࿰…...

利用邮件发送附件来实现一键巡检,附件是通过调用zabbix api生成的word和Excel
HTML部分: <!DOCTYPE html> <html> <head><title>自动巡检</title><!-- 加入CSS样式 --> </head> <body><form id"inspectionForm"><label for"email">邮箱地址:</label>&…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...

Qt的学习(二)
1. 创建Hello Word 两种方式,实现helloworld: 1.通过图形化的方式,在界面上创建出一个控件,显示helloworld 2.通过纯代码的方式,通过编写代码,在界面上创建控件, 显示hello world; …...
