代码随想录刷题题Day29
刷题的第二十九天,希望自己能够不断坚持下去,迎来蜕变。😀😀😀
刷题语言:C++
Day29 任务
● 01背包问题,你该了解这些!
● 01背包问题,你该了解这些! 滚动数组
● 416. 分割等和子集
1 动态规划:01背包问题,你该了解这些!

背包问题的理论基础重中之重是01背包
1.1 01 背包
01 背包:有n件物品和一个最多能背重量为w的背包。第i件物品的重量是weight[i],得到的价值是value[i]。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大

| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
二维dp数组01背包
(1)确定dp数组以及下标的含义
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
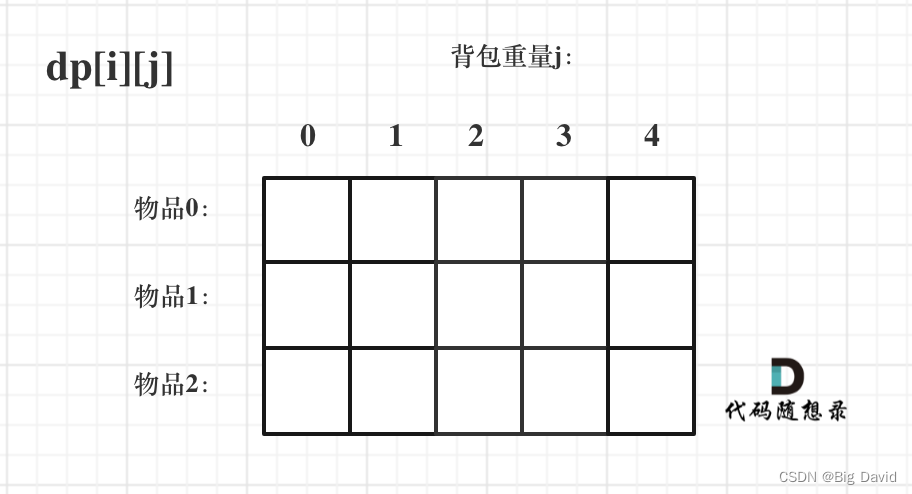
(2)确定递推公式
1.不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
2.放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
(3)dp数组如何初始化
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。如图:
状态转移方程是由 i-1 推导出来,那么i为0的时候就一定要初始化
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品
for (int j = 0; j < weight[0]; j++) {dp[0][j] = 0;
}
for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];
}
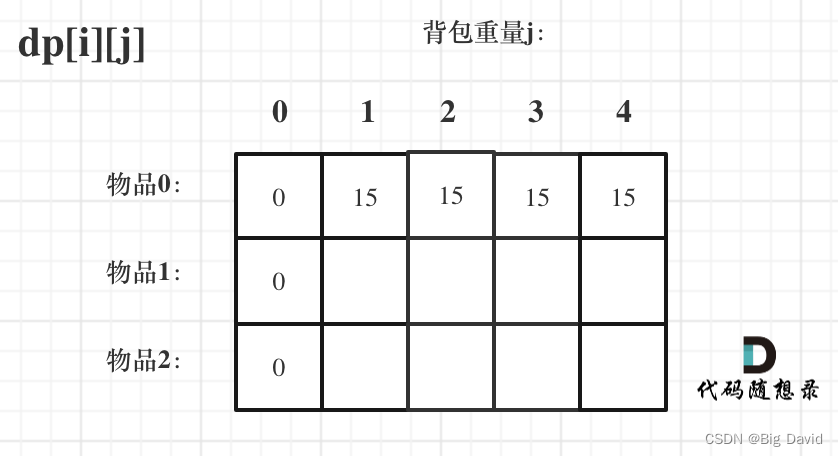
dp[0][j] 和 dp[i][0] 都已经初始化,其他下标的初始化什么数值都可以,因为都会被覆盖。
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];
}
(4)遍历顺序
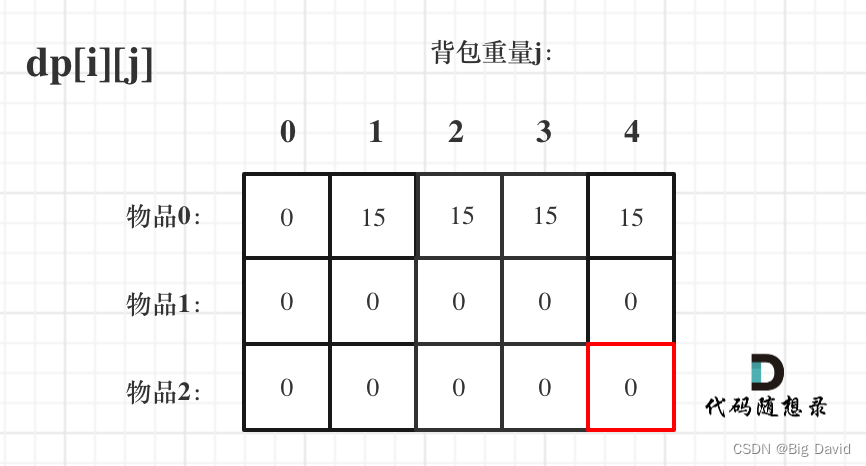
先遍历物品,然后遍历背包重量
for (int i = 1; i < weight.size(); i++) {for (int j = 0; j <= bagweight; j++) {if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}
}
先遍历背包,再遍历物品
// weight数组的大小 就是物品个数
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量for(int i = 1; i < weight.size(); i++) { // 遍历物品if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}
}
(5)举例推导dp数组
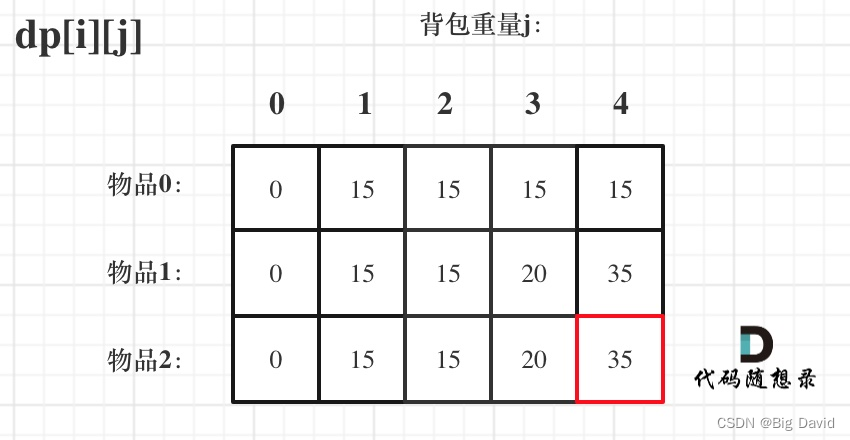
C++:
void test_2_wei_bag_problem1() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagweight = 4;// 二维数组vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));// 初始化for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];}for (int i = 1; i < weight.size(); i++) {for (int j = 0; j <= bagweight; j++) {if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}}cout << dp[weight.size() - 1][bagweight] << endl;
}
int main() {test_2_wei_bag_problem1();
}
2 动态规划:01背包理论基础(滚动数组)
背包最大重量为4。
物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
一维dp数组:上一层可以重复利用,直接拷贝到当前层。
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
(1)确定dp数组的定义
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]
(2)一维dp数组的递推公式
dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
(3)一维dp数组如何初始化
假设物品价值都是大于0的,所以dp数组初始化的时候,都初始为0
(4)一维dp数组遍历顺序
for (int i = 0; i < weight.size(); i++) {// 遍历物品for (int j = bagweight; j >= weight[i]; j--) {// 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
倒序遍历是为了保证物品i只被放入一次! 如果一旦正序遍历了,那么物品0就会被重复加入多次!
为什么二维dp数组遍历的时候不用倒序呢?
因为对于二维dp,dp[i][j]都是通过上一层即dp[i - 1][j]计算而来,本层的dp[i][j]并不会被覆盖!
(5)举例推导dp数组
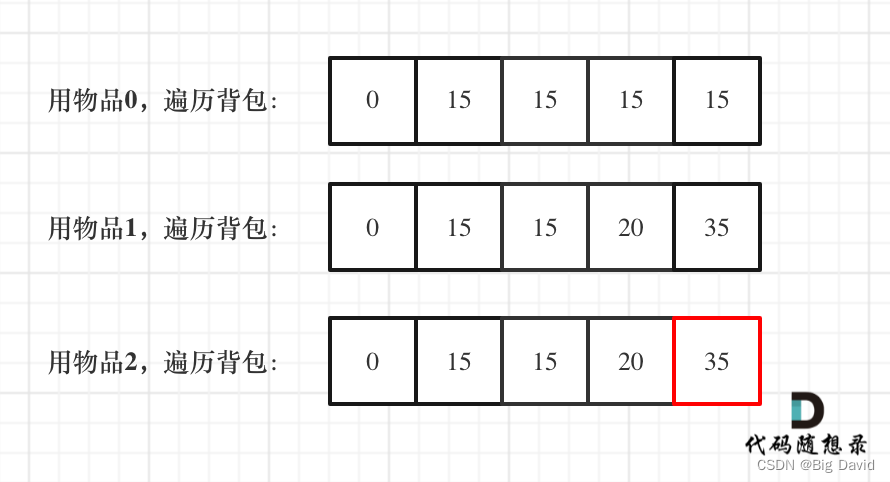
C++:
void test_1_wei_bag_problem() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagWeight = 4;// 初始化vector<int> dp(bagWeight + 1, 0);for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}cout << dp[bagWeight] << endl;
}int main() {test_1_wei_bag_problem();
}
3 分割等和子集
416. 分割等和子集

思路:
背包问题,有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
本题使用的是01背包,因为元素我们只能用一次。
把01背包问题套到本题:
(1)背包的体积为sum / 2
(2)背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
(3)背包如果正好装满,说明找到了总和为 sum / 2 的子集。
(4)背包中每一个元素是不可重复放入。
动态规划
(1)确定dp数组以及下标的含义
01背包中,dp[j] 表示: 容量为j的背包,所背的物品价值最大可以为dp[j]
本题:dp[j]表示 背包总容量(所能装的总重量)是j,放进物品后,背的最大重量为dp[j]
(2)确定递推公式
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题,相当于背包里放入数值,那么物品i的重量是nums[i],其价值也是nums[i]。
所以递推公式:dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
(3)dp数组如何初始化
dp[0]一定是0。
如果题目给的价值都是正整数那么非0下标都初始化为0就可以了,如果题目给的价值有负数,那么非0下标就要初始化为负无穷。
这样才能让dp数组在递推的过程中取得最大的价值,而不是被初始值覆盖了
(4)确定遍历顺序
for (int i = 0; i < nums.size(); i++) {for (int j = target; j >= nums[i]; j--) {// 每一个元素一定是不可重复放入,所以从大到小遍历dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);}
}
(5)举例推导dp数组
dp[j]的数值一定是小于等于j的,如果dp[j] == j 说明,集合中的子集总和正好可以凑成总和j
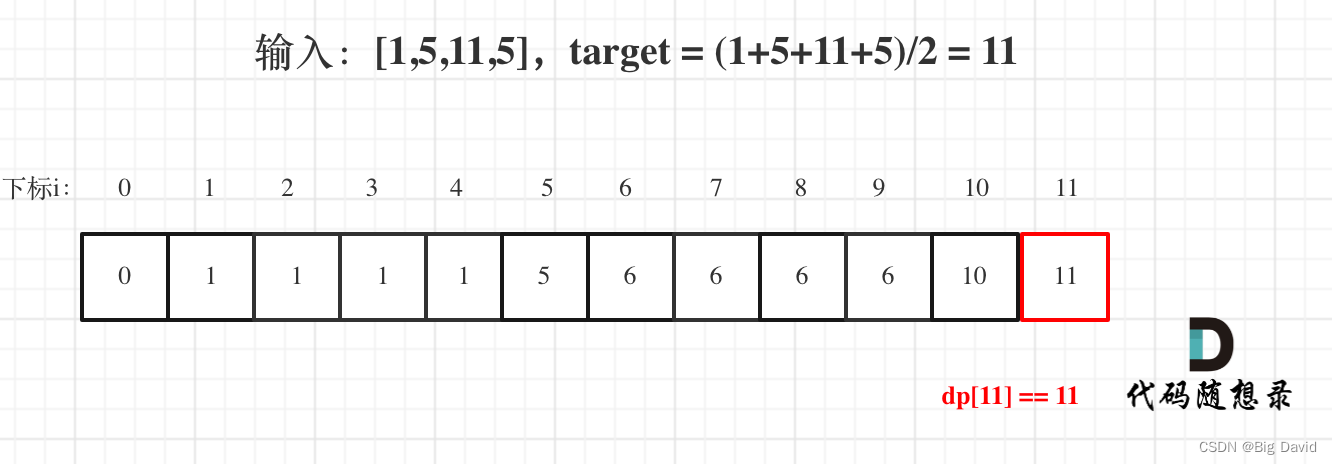
C++:
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0;vector<int> dp(10001, 0);for (int i = 0; i < nums.size(); i++) {sum += nums[i];}if (sum % 2 == 1) return false;int target = sum / 2;// 开始 01背包for(int i = 0; i < nums.size(); i++) {for(int j = target; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入,所以从大到小遍历dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);}}// 集合中的元素正好可以凑成总和targetif (dp[target] == target) return true;return false;}
};
时间复杂度: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( n ) O(n) O(n),虽然dp数组大小为一个常数,但是大常数
鼓励坚持三十天的自己😀😀😀
相关文章:

代码随想录刷题题Day29
刷题的第二十九天,希望自己能够不断坚持下去,迎来蜕变。😀😀😀 刷题语言:C Day29 任务 ● 01背包问题,你该了解这些! ● 01背包问题,你该了解这些! 滚动数组 …...
CVE-2023-51385 OpenSSH ProxyCommand命令注入漏洞
一、背景介绍 ProxyCommand 是 OpenSSH ssh_config 文件中的一个配置选项,它允许通过代理服务器建立 SSH 连接,从而在没有直接网络访问权限的情况下访问目标服务器。这对于需要经过跳板机、堡垒机或代理服务器才能访问的目标主机非常有用。 二、漏洞简…...

如何寻找到相对完整的真正的游戏的源码 用来学习?
在游戏开发的学习之路上,理论与实践是并重的两个方面。对于许多热衷于游戏开发的学习者来说,能够接触到真实的、完整的游戏源码无疑是一个极好的学习机会。但问题来了:我们该如何寻找到这些珍贵的资源呢? 开源游戏项目 GitHub:地…...
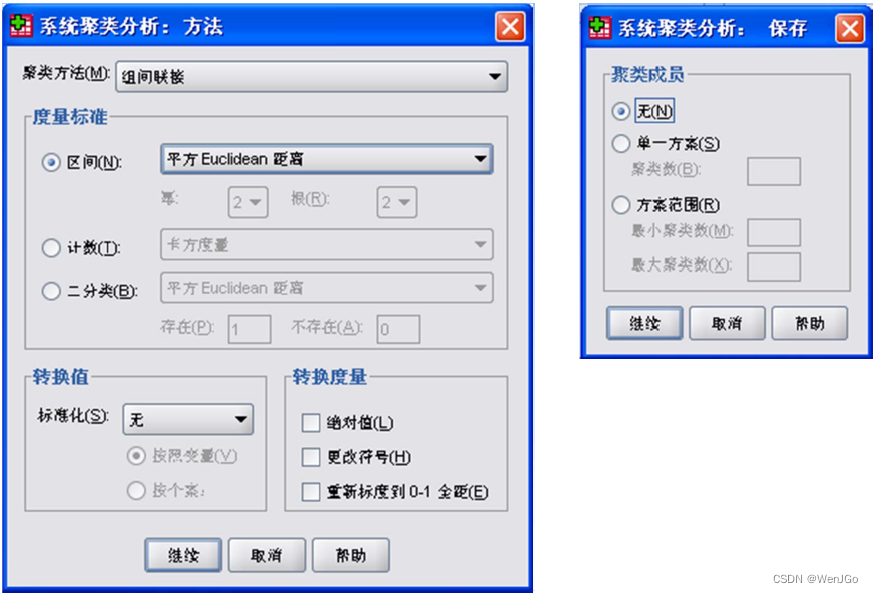
数模学习day11-系统聚类法
本文参考辽宁石油化工大学于晶贤教授的演示文档聚类分析之系统聚类法及其SPSS实现。 目录 1.样品与样品间的距离 2.指标和指标间的“距离” 相关系数 夹角余弦 3.类与类间的距离 (1)类间距离 (2)类间距离定义方式 1.最短…...

SpringBoot+Redis实现接口防刷功能
场景描述: 在实际开发中,当前端请求后台时,如果后端处理比较慢,但是用户是不知情的,此时后端仍在处理,但是前端用户以为没点到,那么再次点击又发起请求,就会导致在短时间内有很多请求…...

TensorRT加速推理入门-1:Pytorch转ONNX
这篇文章,用于记录将TransReID的pytorch模型转换为onnx的学习过程,期间参考和学习了许多大佬编写的博客,在参考文章这一章节中都已列出,非常感谢。 1. 在pytorch下使用ONNX主要步骤 1.1. 环境准备 安装onnxruntime包 安装教程可…...

springboot常用扩展点
当涉及到Spring Boot的扩展和自定义时,Spring Boot提供了一些扩展点,使开发人员可以根据自己的需求轻松地扩展和定制Spring Boot的行为。本篇博客将介绍几个常用的Spring Boot扩展点,并提供相应的代码示例。 1. 自定义Starter(面试常问) Sp…...
19道ElasticSearch面试题(很全)
点击下载《19道ElasticSearch面试题(很全)》 1. elasticsearch的一些调优手段 1、设计阶段调优 (1)根据业务增量需求,采取基于日期模板创建索引,通过 roll over API 滚动索引; (…...

向爬虫而生---Redis 拓宽篇3 <GEO模块>
前言: 继上一章: 向爬虫而生---Redis 拓宽篇2 <Pub/Sub发布订阅>-CSDN博客 这一章的用处其实不是特别大,主要是针对一些地图和距离业务的;就是Redis的GEO模块。 GEO模块是Redis提供的一种高效的地理位置数据管理方案,它允许我们存储和查询…...

Vue项目里实现json对象转formData数据
平常调用后端接口传参都是json对象,当提交表单遇到有附件需要传递时,通常是把附件上传单独做个接口,也有遇到后端让提交接口一并把附件传递到后端,这种情况需要把参数转成formData的数据,需要用到new FormData()。json…...

leetcode刷题记录
栈 2696. 删除子串后的字符串最小长度 哈希表 1. 两数之和 用map来保存每个数和他的索引 383. 赎金信 用map来存储字符的个数 链表 2. 两数相加 指针的移动 动态规划 53. 最大子数组和 2707. 字符串中的额外字符 递归 101. 对称二叉树 数学 1276. 不浪费原料的汉堡…...
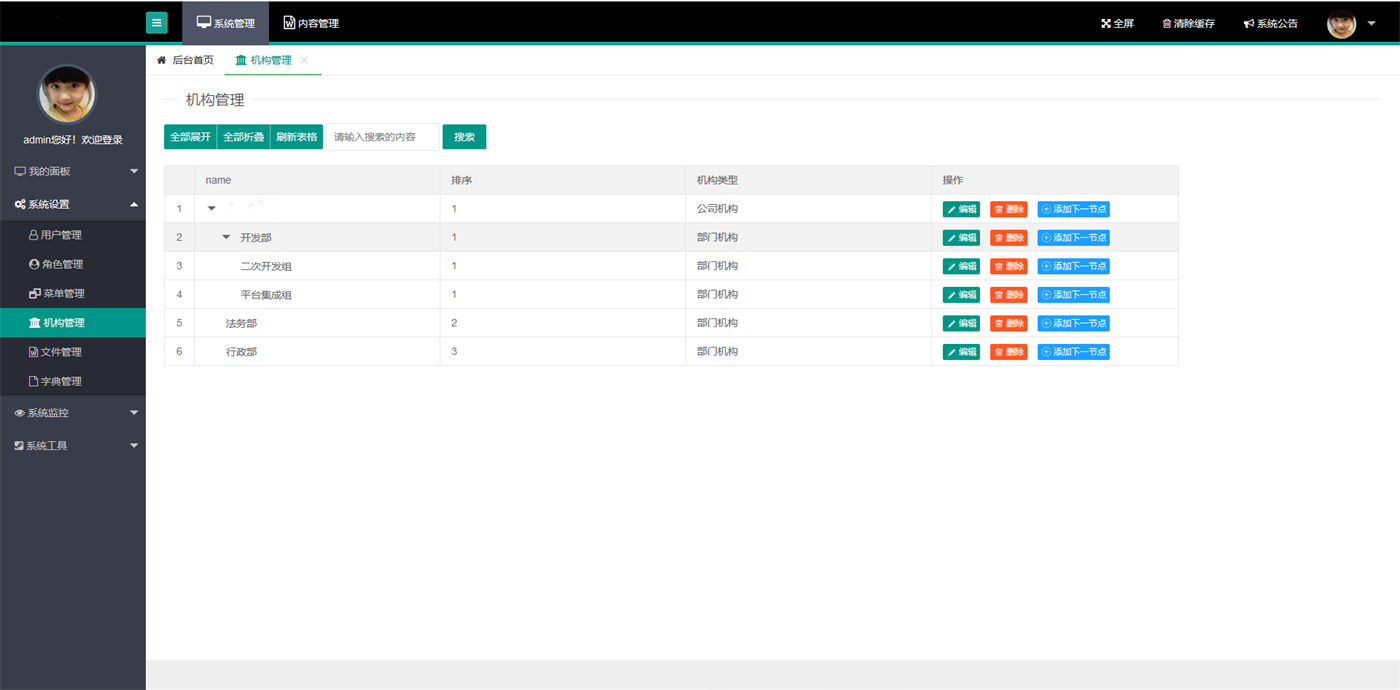
SpringMVC通用后台管理系统源码
整体的SSM后台管理框架功能已经初具雏形,前端界面风格采用了结构简单、 性能优良、页面美观大的Layui页面展示框架 数据库支持了SQLserver,只需修改配置文件即可实现数据库之间的转换。 系统工具中加入了定时任务管理和cron生成器,轻松实现系统调度问…...

深度解析Dubbo的基本应用与高级应用:负载均衡、服务超时、集群容错、服务降级、本地存根、本地伪装、参数回调等关键技术详解
负载均衡 官网地址: http://dubbo.apache.org/zh/docs/v2.7/user/examples/loadbalance/ 如果在消费端和服务端都配置了负载均衡策略, 以消费端为准。 这其中比较难理解的就是最少活跃调用数是如何进行统计的? 讲道理, 最少活跃数…...

备战2024美赛数学建模,文末获取历史优秀论文
总说(历年美赛优秀论文可获取) 数模的题型千变万化,我今天想讲的主要是一些「画图」、「建模」、「写作」和「论文结构」的思路,这些往往是美赛阅卷官最看重的点,突破了这些点,才能真正让你的美赛论文更上…...
)
Java加密解密大全(MD5、RSA)
目录 一、MD5加密二、RSA加解密(公加私解,私加公解)三、RSA私钥加密四、RSA私钥加密PKCS1Padding模式 一、MD5加密 密文形式:5eb63bbbe01eeed093cb22bb8f5acdc3 import java.math.BigInteger; import java.security.MessageDigest; import java.security…...
)
C语言程序设计考试掌握这些题妥妥拿绩点(写给即将C语言考试的小猿猴们)
目录 开篇说两句1. 水仙花数题目描述分析代码示例 2. 斐波那契数列题目描述分析代码示例 3. 猴子吃桃问题题目描述分析代码示例 4. 物体自由落地题目描述分析代码示例 5. 矩阵对角线元素之和题目描述分析代码示例 6. 求素数题目描述分析代码示例 7. 最大公约数和最小公倍数题目…...
编译ZLMediaKit(win10+msvc2019_x64)
前言 因工作需要,需要ZLMediaKit,为方便抓包分析,最好在windows系统上测试,但使用自己编译的第三方库一直出问题,无法编译通过。本文档记录下win10上的编译过程,供有需要的小伙伴使用 一、需要安装的软件…...
JS-基础语法(一)
JavaScript简单介绍 变量 常量 数据类型 类型转换 案例 1.JavaScript简单介绍 JavaScript 是什么? 是一种运行在客户端(浏览器)的编程语言,可以实现人机交互效果。 JS的作用 JavaScript的组成 JSECMAScript( 基础语法 )…...
18款Visual Studio实用插件(更新)
前言 俗话说的好工欲善其事必先利其器,安装一些Visual Studio实用插件对自己日常的开发和工作效率能够大大的提升,避免996从选一款好的IDE实用插件开始。以下是我认为比较实用的Visual Studio插件希望对大家有用,大家有更好的插件推荐可在文…...
)
三、java线性表(顺序表、链表、栈、队列)
java线性表 三、线性表1.1 顺序表1.2 链表1.2.1 单向链表(Singly Linked List)1.2.2 双向链表(Doubly Linked List) 1.3 LinkedList VS ArrayList1.3.7 使用 LinkedList 的场景 1.4 栈1.5 队列 三、线性表 线性表是一种经典的数据…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...