朴素贝叶斯法学习笔记
频率派和贝叶斯派
频率派认为可以通过大量实验,从样本推断总体。比如假定总体服从均值为μ\muμ,方差为σ\sigmaσ的分布。根据中心极限定理,是可以通过抽样估算总体的参数的,而且抽样次数越多,对总体的估计就越准确。需要指出的是,频率派的观点认为μ\muμ和σ\sigmaσ都是固定,就是说他们都是某个确定的值。
但实际上,实验次数越多,成本就越高,而且很多时候是没有办法进行多次试验的。这时候,频率派对总体参数的估计就会存在较大偏差。
贝叶斯派则认为,可以先对总体的参数进行粗略估计(先验概率),然后根据实验结果不断调整参数的估计值(后验概率)。而且,贝叶斯派认为参数并不是固定的,而是服从某个概率分布的值。
朴素贝叶斯法
独立同分布假设
假设训练数据集T=(x1,y1),(x2,y2),...,(xn,yn)T={(x_1,y_1) ,(x_2,y_2),...,(x_n,y_n)}T=(x1,y1),(x2,y2),...,(xn,yn),可以理解为每个xxx都代表了一个完整的case。比如x1x_1x1可以用x1(1)x_1^{(1)}x1(1)来表示第一个样本的第1个特征,而一个样本可以有多个特征,比如x1(k)x_1^{(k)}x1(k)就表示第1个样本的第kkk个特征;而y1y_1y1就表示这个x1x_1x1这个case所属的类。
书上还有一句话,训练集是独立同分布的。也就是说所使用的到的样本都是从同一个总体中拿出来的,自然就服从同一个分布;如果不服从同分布,也就意味着我们无法得到最终的模型,我们只能根据不同的case得到不同的模型。独立就是说各样本之间互不影响,得到什么样的yyy值,只要看自己有什么样的xxx就可以了,x1x_1x1不用去管x2x_2x2的y2y_2y2值是怎么得到的。
学习过程
朴素贝叶斯法的最终目的是通过训练集学习xxx和yyy的联合概率分布P(X,Y)P(X,Y)P(X,Y)。这样当我们知道某个测试样本的XXX,我们就可以根据联合概率分布求出YYY的概率分布。然后我们看哪个YYY能够让P(X,Y)P(X,Y)P(X,Y)最大,我们就把这个YYY作为这个测试样本XXX的类别。
我们假设YYY有kkk个不同的取值,也就是说样本一共有kkk类。而我们一共有nnn个特征,Xi(1),Xi(2),...,Xi(n)X_i^{(1)},X_i^{(2)},...,X_i^{(n)}Xi(1),Xi(2),...,Xi(n)。
而为了通过训练集学到联合概率分布P(X,Y)P(X,Y)P(X,Y),我们需要分别学到先验概率分布P(Y=ck)P(Y=c_k)P(Y=ck)以及条件概率分布P(X(1)=x(1),X(2)=x(2),...,X(n)=x(n)∣Y=ck)P(X^{(1)}=x^{(1)},X^{(2)}=x^{(2)},...,X^{(n)}=x^{(n)}|Y=c_k)P(X(1)=x(1),X(2)=x(2),...,X(n)=x(n)∣Y=ck)
这是因为当我们拿到测试数据集的时候,我们面临的问题是求:
P(Y=ck∣X(1)=x(1),X(2)=x(2),...,X(n)=x(n))P(Y=c_k|X^{(1)}=x^{(1)},X^{(2)}=x^{(2)},...,X^{(n)}=x^{(n)})P(Y=ck∣X(1)=x(1),X(2)=x(2),...,X(n)=x(n))
这是一个条件概率求解,而根据贝叶斯公式,我们知道:
P(A∣B)=P(A)P(B∣A)P(B)P(A|B)=\frac{P(A)P(B|A)}{P(B)}P(A∣B)=P(B)P(A)P(B∣A)
所以上面那个条件概率就等于:
P(Y=ck)P(X(1)=x(1),X(2)=x(2),...,X(n)=x(n)∣Y=ck)P(X(1)=x(1),X(2)=x(2),...,X(n)=x(n)), (1)\frac{P(Y=c_k)P(X^{(1)}=x^{(1)},X^{(2)}=x^{(2)},...,X^{(n)}=x^{(n)}|Y=c_k)}{P(X^{(1)}=x^{(1)},X^{(2)}=x^{(2)},...,X^{(n)}=x^{(n)})} \text{, \tag{1}}P(X(1)=x(1),X(2)=x(2),...,X(n)=x(n))P(Y=ck)P(X(1)=x(1),X(2)=x(2),...,X(n)=x(n)∣Y=ck), (1)
而且我们知道朴素贝叶斯之所以朴素,就是因为这个算法假定各特征都是独立的。也就是说X(1)X^{(1)}X(1)、X(2)X^{(2)}X(2)……X(n)X^{(n)}X(n)的互不影响,没有关系。其实相当于是把问题简单化了。有了这个条件,公式1就可以进一步化简:
P(X(1)=x(1),X(2)=x(2),...,X(n)=x(n))=∏i=1nP(X(i)=x(i))P(X^{(1)}=x^{(1)},X^{(2)}=x^{(2)},...,X^{(n)}=x^{(n)})=\prod_{i=1}^nP(X^{(i)}=x^{(i)})P(X(1)=x(1),X(2)=x(2),...,X(n)=x(n))=i=1∏nP(X(i)=x(i))
P(X(1)=x(1),X(2)=x(2),...,X(n)=x(n)∣Y=ck)=∏i=1nP(X(i)=x(i)∣Y=ck)P(X^{(1)}=x^{(1)},X^{(2)}=x^{(2)},...,X^{(n)}=x^{(n)}|Y=c_k)=\prod_{i=1}^nP(X^{(i)}=x^{(i)}|Y=c_k)P(X(1)=x(1),X(2)=x(2),...,X(n)=x(n)∣Y=ck)=i=1∏nP(X(i)=x(i)∣Y=ck)
所以公式1最后就变成了:
f1=P(Y=ck)∏i=1nP(X(i)=x(i)∣Y=ck)∏i=1nP(X(i)=x(i))(2)f_1=\frac{P(Y=c_k)\prod_{i=1}^nP(X^{(i)}=x^{(i)}|Y=c_k)}{\prod_{i=1}^nP(X^{(i)}=x^{(i)})} \text{\tag{2}}f1=∏i=1nP(X(i)=x(i))P(Y=ck)∏i=1nP(X(i)=x(i)∣Y=ck)(2)
我们知道,现在有了样本X(i)=x(i)X^{(i)}=x^{(i)}X(i)=x(i),现在要求的是当f1f_1f1最大的时候,ckc_kck是多少?也就是说现在ckc_kck是未知量,而跟X(i)X^{(i)}X(i)相关的都是由数据集提供的,所以求f1f_1f1的最大值就等价于求f2f_2f2的最大值,二者的最大值不一样(我们也不关心),但取得最大值时的ckc_kck是相等的。
f2=P(Y=ck)∏i=1nP(X(i)=x(i)∣Y=ck)(3)f_2=P(Y=c_k)\prod_{i=1}^nP(X^{(i)}=x^{(i)}|Y=c_k) \text{\tag{3}}f2=P(Y=ck)i=1∏nP(X(i)=x(i)∣Y=ck)(3)
参数估计
极大似然估计
朴素贝叶斯法意味着我们要估计P(Y=ck)P(Y=c_k)P(Y=ck)以及P(X(i)=x(i)∣Y=ck)P(X^{(i)}=x^{(i)}|Y=c_k)P(X(i)=x(i)∣Y=ck)。
先验概率P(Y=ck)P(Y=c_k)P(Y=ck)的极大似然估计是:
P(Y=ck)=∑i=1nI(yi=ck)N,k=1,2...KP(Y=c_k)=\frac{\sum\limits_{i=1}^nI(y_i=c_k)}{N} \text ,k=1,2...KP(Y=ck)=Ni=1∑nI(yi=ck),k=1,2...K
而每个特征X(i)X^{(i)}X(i)都可能有很多个取值,所以假设第iii个特征X(i)X^{(i)}X(i)的可能取值为结合{ai1,ai2...aiSi}\lbrace{a_{i1},a_{i2}...a_{iS_i}}\rbrace{ai1,ai2...aiSi},也就是说我们假设第iii个特征可能的取值SiS_iSi种。
条件概率的极大似然估计是:P(X(i)=ail∣Y=ck)=∑i=1nI(xj(i)=ail,yi=ck)∑i=1nI(yi=ck)P(X^{(i)}=a_{il}|Y=c_k)=\frac{\sum\limits_{i=1}^n I(x^{(i)}_j=a_{il},y_i=c_k)}{\sum\limits_{i=1}^nI(y_i=c_k)}P(X(i)=ail∣Y=ck)=i=1∑nI(yi=ck)i=1∑nI(xj(i)=ail,yi=ck)
上式小标太多,解释一下,xj(i)x^{(i)}_jxj(i)表示第jjj个样本的第iii个特征,aila_{il}ail表示第iii个特征的取值为aila_{il}ail。
III为指示函数,也就是说当括号中的关系成立时,I=1I=1I=1,不成立时,I=0I=0I=0。
所以从这里也可以看出来,这个参数的估计过程就是“数数”。先验概率就是数Y=ckY=c_kY=ck出现多少次,占比多少。条件概率就是数Y=ckY=c_kY=ck的时候,x(i)x^{(i)}x(i)这个特征取aila_{il}ail出现多少次,占比多少。可想而知,这是一项庞大的“数数”工程。
贝叶斯估计
极大似然估计可能会发生一个比较尴尬的事情,比如我们就假设样本的第3个特征X(3)X^{(3)}X(3)在训练集中所有取值为{1,3,5}\lbrace1,3,5\rbrace{1,3,5},但是在测试集中,出现一个新值4。这时,如果按照极大似然法,条件概率P(X(i)=4∣Y=ck)=0P(X^{(i)}=4|Y=c_k)=0P(X(i)=4∣Y=ck)=0(因为训练集没有这个4,所以从训练集学到的条件概率就是0)。而目标函数f2f_2f2是一系列条件概率的累乘,所以最后无论其他特征的条件概率是多少,f2f_2f2恒等于0。
也就意味着学到的这个联合分布,过拟合了,对新出现的数据预测能力极差。
为了避免这一现象,现在需要引入贝叶斯估计,其实也可以理解为正则化的手段。具体的,条件概率的贝叶斯估计是:P(X(i)=ail∣Y=ck)=∑i=1nI(xj(i)=ail,yi=ck)+λ∑i=1nI(yi=ck)+SiλP(X^{(i)}=a_{il}|Y=c_k)=\frac{\sum\limits_{i=1}^n I(x^{(i)}_j=a_{il},y_i=c_k)+\lambda}{\sum\limits_{i=1}^nI(y_i=c_k)+S_i\lambda}P(X(i)=ail∣Y=ck)=i=1∑nI(yi=ck)+Siλi=1∑nI(xj(i)=ail,yi=ck)+λ
上式中,λ≥0\lambda\geq0λ≥0,显而易见,当λ=0\lambda=0λ=0的时候就是极大似然估计。根据习惯,经常取λ=1\lambda=1λ=1,此时称为拉普拉斯平滑。
同样,也为了避免先验概率等于0,同样可以引入贝叶斯估计:P(Y=ck)=∑i=1nI(yi=ck)+λN+KλP(Y=c_k)=\frac{\sum\limits_{i=1}^nI(y_i=c_k)+\lambda}{N+K\lambda}P(Y=ck)=N+Kλi=1∑nI(yi=ck)+λ
由于当λ=1\lambda=1λ=1,并且在样本量NNN越来越大的时候,λ\lambdaλ对先验概率和条件概率的影响就会越来越小,甚至忽略不计。这就是所谓的拉普拉斯平滑的思想。
相关文章:

朴素贝叶斯法学习笔记
频率派和贝叶斯派 频率派认为可以通过大量实验,从样本推断总体。比如假定总体服从均值为μ\muμ,方差为σ\sigmaσ的分布。根据中心极限定理,是可以通过抽样估算总体的参数的,而且抽样次数越多,对总体的估计就越准确。…...

vscode与C++安装与使用【不好用来骂我】
网上教程很多,但是都不太好用,这是我垃圾堆里淘金淘出来的教程: 安装软件 安装 Visual Studio Code: 你需要下载并安装 Visual Studio Code,可以在官网下载 https://code.visualstudio.com/download。 安装 C 扩展: 在 Visual S…...
计算相似度实现性能优化)
C++11使用多线程(线程池)计算相似度实现性能优化
需求:图像识别中,注册的样本多了会影响计算速度,成为性能瓶颈,其中一个优化方法就是使用多线程。例如,注册了了3000个特征,每个特征4096个float。可以把3000个特征比对放到4个线程中进行计算,然…...
【测绘程序设计】——平面坐标转换
测绘工程中经常遇到平面坐标转换——比如,北京54(或西安80)平面坐标转换成CGCS2000平面坐标、工程独立坐标系平面坐标转换成CGCS2000平面坐标等,常用转换模型包括:①三参数法(2平移+1旋转);②四参数法(赫尔默特法,2平移+1旋转+1尺度);③六参数法(仿射变换法,2平移…...
五子棋的设计与实现
术:Java等摘要:五子棋是一种两人对弈的纯策略型棋类游戏,非常容易上手,老少皆宜。为了更好的推广五子棋,研究简单的人工智能方式,运用Java开发五子棋游戏。主要包含了人机对战,棋盘初始化&#…...

大数据项目软硬件选择
目录 一.技术选型 二.系统数据流程设计 三.框架版本选型 如何选择Apache/CDH/HDP版本...
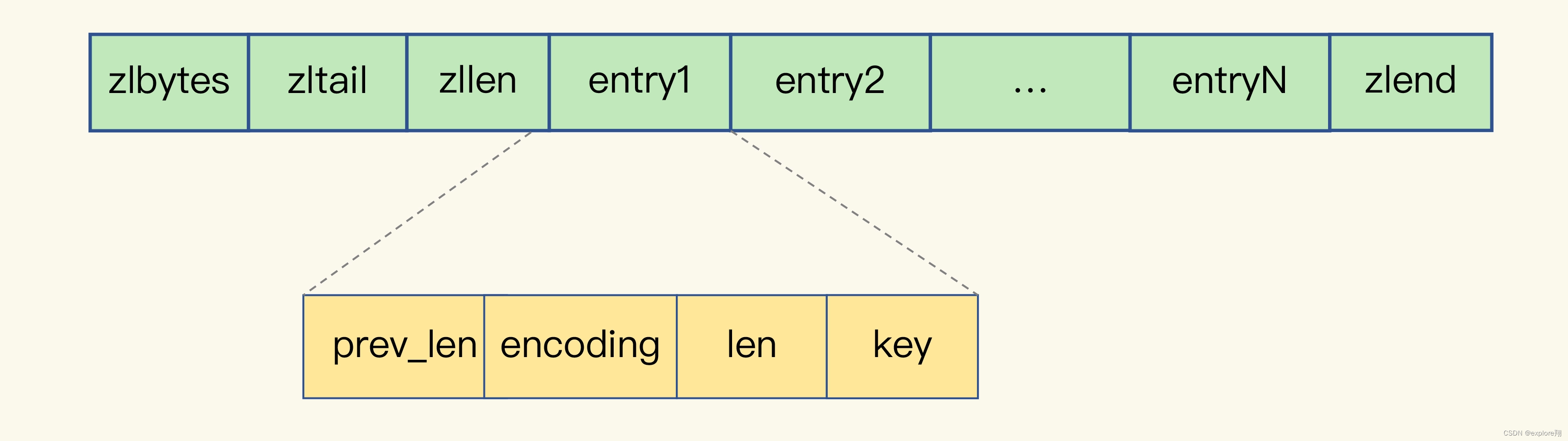
redis数据结构的适用场景分析
1、String 类型的内存空间消耗问题,以及选择节省内存开销的数据类型的解决方案。 为什么 String 类型内存开销大? 图片 ID 和图片存储对象 ID 都是 10 位数,我们可以用两个 8 字节的 Long 类型表示这两个 ID。因为 8 字节的 Long 类型最大可以…...

同步、异步、全双工、半双工的区别
1、通讯 1.1 并行通讯 定义:一条信息的各位数据被同时传送的通讯方式称为并行通讯; 特点: 各个数据位同时发送,传送速度快、效率高,但有多少数据位就需要多少根数据线,因此传送成本高,并且只…...

ClickHouse 与 Amazon S3 结合?一起来探索其中奥秘
目录ClickHouse 简介ClickHouse 与对象存储ClickHouse 与 S3 结合的三种方法示例参考架构小结参考资料ClickHouse 简介ClickHouse 是一种快速的、开源的、用于联机分析(OLAP)的列式数据库管理系统(DBMS),由俄罗斯的Yan…...
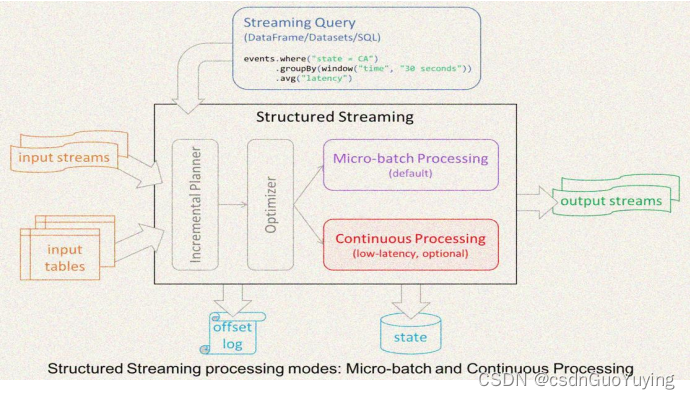
【Spark分布式内存计算框架——Structured Streaming】1. Structured Streaming 概述
前言 Apache Spark在2016年的时候启动了Structured Streaming项目,一个基于Spark SQL的全新流计算引擎Structured Streaming,让用户像编写批处理程序一样简单地编写高性能的流处理程序。 Structured Streaming并不是对Spark Streaming的简单改进…...
【Windows】【Linux】---- Java证书导入
问题: PKIX path building failed: sun.security.provider.certpath.SunCertPathBuilderException: unable to find valid certification path to requested target 无法找到请求目标的有效证书路径 一、Windows—java证书导入 1、下载证书到本地(以下…...

【Linux学习】菜鸟入门——gcc与g++简要使用
一、gcc/g gcc/g是编译器,gcc是GCC(GUN Compiler Collection,GUN编译器集合)中的C编译器;g是GCC中的C编译器。使用g编译文件时会自动链接STL标准库,而gcc不会自动链接STL标准库。下面简单介绍一下Linux环境下(Windows差…...

Cadence Allegro 导出Bill of Material Report详解
⏪《上一篇》 🏡《总目录》 ⏩《下一篇》 目录 1,概述2,Assigned Functions Report作用3,Assigned Functions Report示例4,Assigned Functions Report导出方法4.1,方法14.2,方法2B站关注“硬小二”浏览更多演示视频...
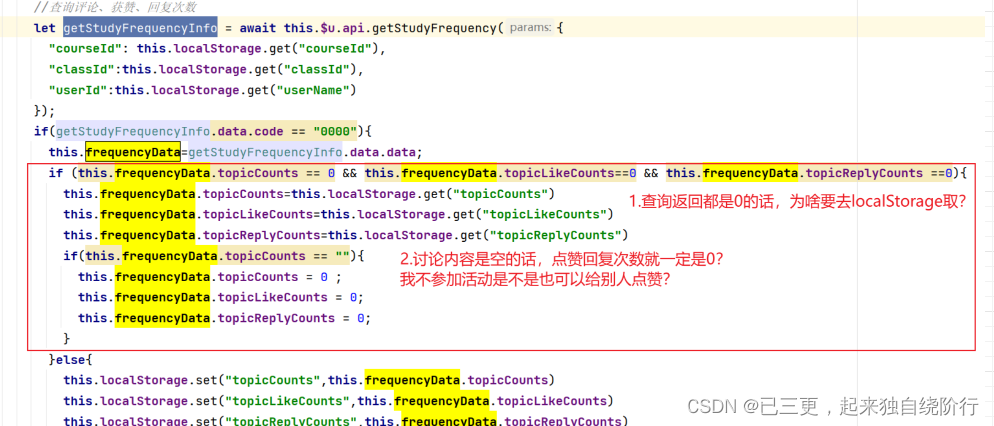
localStorage线上问题的思考
一、背景: localStorage作为HTML5 Web Storage的API之一,使用标准的键值对(Key-Value,简称KV)数据类型主要作用是本地存储。本地存储是指将数据按照键值对的方式保存在客户端计算机中,直到用户或者脚本主动清除数据&a…...

什么是DNS域名解析
什么是DNS域名解析?因特网上作为域名和IP地址相互映射的一个分布式数据库,能够使用户更方便的访问互联网,而不用去记住能够被机器直接读取的IP数串。通过主机名,得到该主机名对应的IP地址的过程叫做域名解析。正向解析:…...

Cadence Allegro 导出Assigned Functions Report详解
⏪《上一篇》 🏡《总目录》 ⏩《下一篇》 目录 1,概述2,Assigned Functions Report作用3,Assigned Functions Report示例4,Assigned Functions Report导出方法4.1,方法14.2,方法2B站关注“硬小二”浏览更多演示视频...

Python中Opencv和PIL.Image读取图片的差异对比
近日,在进行深度学习进行推理的时候,发现不管怎么样都得不出正确的结果,再仔细和正确的代码进行对比了后发现原来是Python中不同的库读取的图片数组是有差异的。 image np.array(Image.open(image_file).convert(RGB)) image cv2.imread(…...
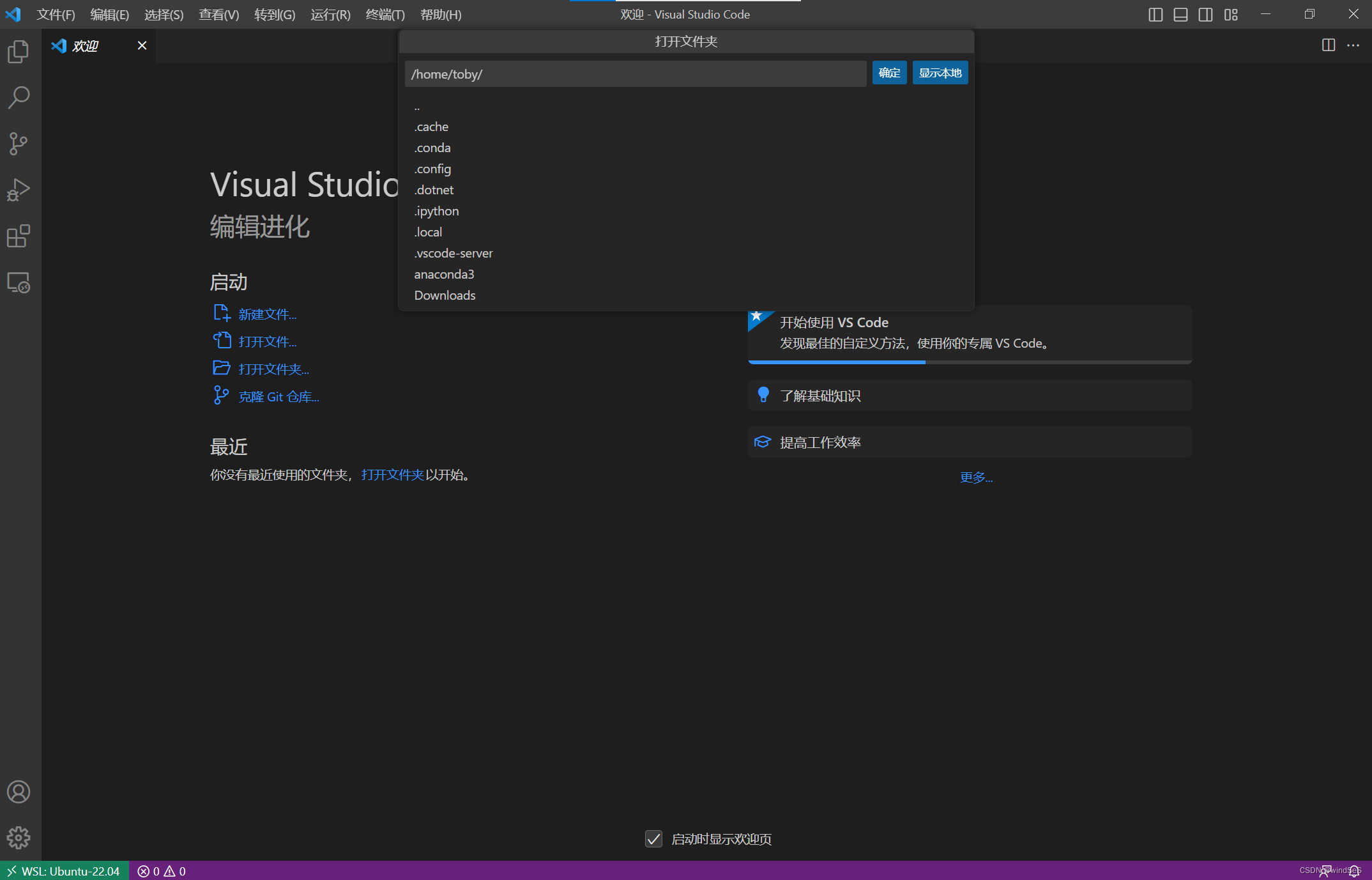
win10 WSL2 使用Ubuntu配置与安装教程
Win10 22H2ubuntu 22.04ROS2 文章目录一、什么是WSL2二、Win10 系统配置2.1 更新Windows版本2.2 Win10系统启用两个功能2.3 Win10开启BIOS/CPU开启虚拟化(VT)(很关键)2.4 下载并安装wsl_update_x64.msi2.5 PowerShell安装组件三、PowerShell安装Ubuntu3.…...
)
LeetCode每日一题(28. Find the Index of the First Occurrence in a String)
Given two strings needle and haystack, return the index of the first occurrence of needle in haystack, or -1 if needle is not part of haystack. Example 1: Input: haystack “sadbutsad”, needle “sad” Output: 0 Explanation: “sad” occurs at index 0 and…...
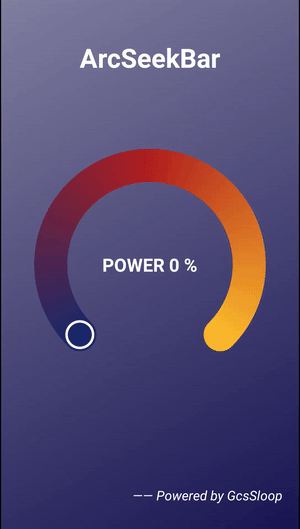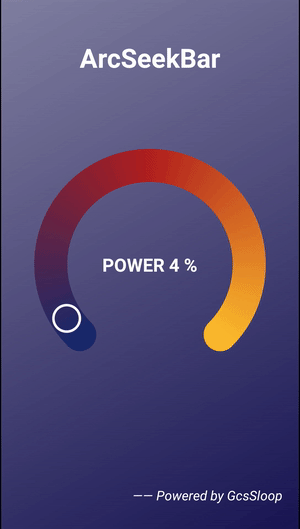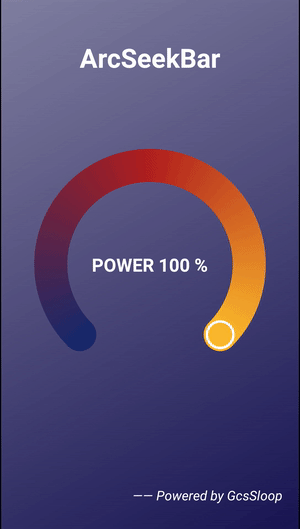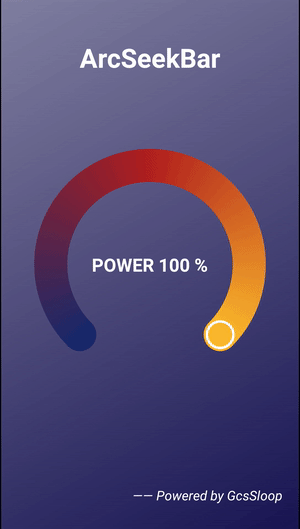
Android 圆弧形 SeekBar
效果预览package com.gcssloop.widget;import android.annotation.SuppressLint;import android.content.Context;import android.content.res.TypedArray;import android.graphics.Canvas;import android.graphics.Color;import android.graphics.Matrix;import android.graph…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...
