动态规划算法
1.应用场景-背包问题
背包问题:有一个背包,容量为 4 磅 , 现有如下物品
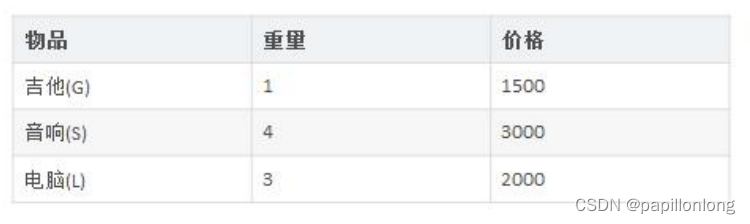
- 要求达到的目标为装入的背包的总价值最大,并且重量不超出
- 要求装入的物品不能重复
2.动态规划算法介绍
- 动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为小问题进行解决,从而一步步获取最优解
的处理算法 - 动态规划算法与分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这
些子问题的解得到原问题的解。 - 与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。 ( 即下一个子
阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解 ) - 动态规划可以通过填表的方式来逐步推进,得到最优解.
3.动态规划算法最佳实践-背包问题
背包问题:有一个背包,容量为 4 磅 , 现有如下物品
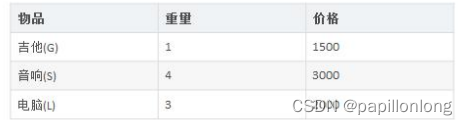
- 要求达到的目标为装入的背包的总价值最大,并且重量不超出
- 要求装入的物品不能重复
思路分析和图解
- 背包问题主要是指一个给定容量的背包、若干具有一定价值和重量的物品,如何选择物品放入背包使物品的价
值最大。其中又分 01 背包和完全背包(完全背包指的是:每种物品都有无限件可用) - 这里的问题属于 01 背包,即每个物品最多放一个。而无限背包可以转化为 01 背包。
- 算法的主要思想,利用动态规划来解决。每次遍历到的第 i 个物品,根据 w[i]和 v[i]来确定是否需要将该物品
放入背包中。即对于给定的 n 个物品,设 v[i]、w[i]分别为第 i 个物品的价值和重量,C 为背包的容量。再令 v[i][j]
表示在前 i 个物品中能够装入容量为 j 的背包中的最大价值。则我们有下面的结果
(1) v[i][0]=v[0][j]=0; //表示 填入表 第一行和第一列是 0
(2) 当 w[i]> j 时:v[i][j]=v[i-1][j] // 当准备加入新增的商品的容量大于 当前背包的容量时,就直接使用上一个
单元格的装入策略
(3) 当 j>=w[i]时: v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]}
// 当 准备加入的新增的商品的容量小于等于当前背包的容量, // 装入的方式:
v[i-1][j]: 就是上一个单元格的装入的最大值
v[i] : 表示当前商品的价值
v[i-1][j-w[i]] : 装入 i-1 商品,到剩余空间 j-w[i]的最大值
当 j>=w[i]时: v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]} :
- 图解的分析
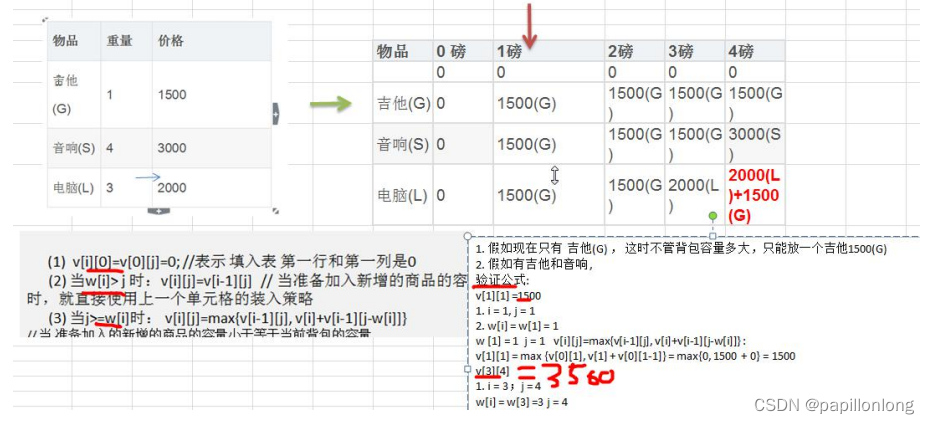
4.动态规划-背包问题的代码实现
public class KnapsackProblem {public static void main(String[] args) {// TODO Auto-generated method stubint[] w = { 1, 4, 3 };// 物品的重量int[] val = { 1500, 3000, 2000 };// 物品的价值 这里val[i] 就是前面讲的v[i]int m = 4;// 背包的容量int n = val.length;// 物品的个数// 创建二维数组// v[i][j]表示在前i个物品中能够装入容量为j的背包中的最大价值int[][] v = new int[n + 1][m + 1];// 初始化第一行和第一列,这里在本程序中,可以不去处理,因为默认就是0for (int i = 0; i < v.length; i++) {v[i][0] = 0;// 将第一列设置为0}for (int i = 0; i < v[0].length; i++) {v[0][i] = 0;// 将第一行设置0}// 根据前面得到的公式来动态规划处理for (int i = 1; i < v.length; i++) {// 不处理第一行 i是从1开始的for (int j = 1; j < v[0].length; j++) {// 不处理第一列,j是从1开始的// 公式if (w[i - 1] > j) {// 因为我们程序i是从1开始的,因此原来公式中的w[i]修改成w[i-1]v[i][j] = v[i - 1][j];} else {// 说明// 因为我们的i从1开始的,因此公式需要调整成// v[i][j]=Math.max(v[i-1][j],val[i-1]+v[i-1][j-w[i-1]]);v[i][j] = Math.max(v[i - 1][j], val[i - 1] + v[i - 1][j - w[i - 1]]);}}}// 输出一下v 看看目前情况for (int i = 0; i < v.length; i++) {for (int j = 0; j < v[i].length; j++) {System.out.print(v[i][j] + " ");}System.out.println();}}}
相关文章:

动态规划算法
1.应用场景-背包问题 背包问题:有一个背包,容量为 4 磅 , 现有如下物品 要求达到的目标为装入的背包的总价值最大,并且重量不超出要求装入的物品不能重复 2.动态规划算法介绍 动态规划(Dynamic Programming)算法的核心思想是&…...
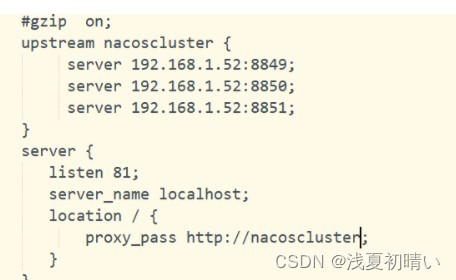
nacos的单机模式和集群模式
文章目录 目录 文章目录 前言 一、nacos数据库配置 二、单机模式 三、集群模式 四、使用nginx集群模式的负载均衡 总结 前言 一、nacos数据库配置 在数据库中创建nacos_config 编码格式utf8-mb4的数据库 把上面的数据库文件导入数据库 在 配置文件中添加如下 spring.datasour…...
Spring Boot 整合定时任务完成 从0 到1
Java 定时任务学习 定时任务概述 > 定时任务的应用场景非常广泛, 如果说 我们想要在某时某地去尝试的做某件事 就需要用到定时任务来通知我们 ,大家可以看下面例子 如果需要明天 早起,哪我们一般会去定一个闹钟去通知我们, 而在编程中 有许许多多的…...

Dialogue Transformers
Abstract 本文介绍了一种基于 Transformer 架构的 对话策略,其中自注意力机制被应用于对话轮次(dialogue turns)的序列上。近期的一些工作使用层次化的循环神经网络(hierarchical recurrent neural networks)在对话上下文中对多个话语(utterances)进行编码,但是我们认…...
【遇见青山】项目难点:缓存击穿问题解决方案
【遇见青山】项目难点:缓存击穿问题解决方案1.缓存击穿互斥锁🔒方案逻辑过期方案2.基于互斥锁方案的具体实现3.基于逻辑过期方案的具体实现1.缓存击穿 缓存击穿问题也叫热点Key问题,就是一个被高并发访问并且缓存重建业务较复杂的key突然失效…...
)
2023Flag具体实施计划(短期)
重新看了flag ,要做的事情太多,太杂,上周一周时间都在纠结和琢磨,该怎么下手。如何达成小目标。特别是沟通,汇报,演讲能力, 以及整体体系化的思维能力的训练。如何做到多思考,而不是瞎搞。这边重…...
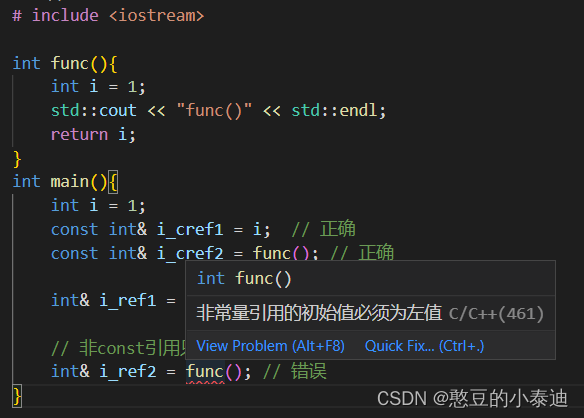
研一寒假C++复习笔记--左值和右值的理解和使用
目录 1--左值和右值的定义 2--简单理解左值和右值的代码 3--非const引用只能接受左值 1--左值和右值的定义 左值:L-Value,L理解为 Location,表示可寻; 右值:R-Value,R理解为 Read,表示可读&a…...

Android 11.0 动态修改SystemProperties中ro开头系统属性的值
需求: 在11.0的产品开发中,对于定制功能的需求很多,有些机型要求可以修改系统属性值,对于系统本身在10.0以后为了系统安全性,不允许修改ro开头的SystemProperties的值,所以如果要求修改ro的相关系统属性&am…...

为什么分库分表
系列文章目录 文章目录系列文章目录前言一、什么是分库分表二、分库分表的原因分库分表三、如何分库分表3.1 垂直拆分1.垂直分库2、垂直分表3.2 水平拆分水平分库水平分表水平分库分表的策略hash取模算法range范围rangehash取模混合地理位置分片预定义算法四、分库分表的问题分…...

1625_MIT 6.828 stabs文档信息整理_下
全部学习汇总: GreyZhang/g_unix: some basic learning about unix operating system. (github.com) 继续之前的学习笔记,整理一下最近看过的一点stabs资料。 这一页中有一半的信息是Fortran专用的,直接跳过。参数的符号修饰符是p,…...
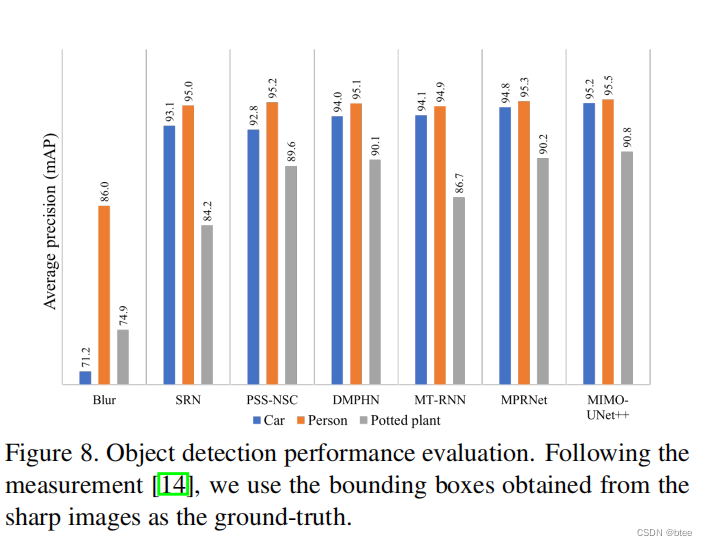
论文阅读 | Rethinking Coarse-to-Fine Approach in Single Image Deblurring
前言:ICCV2021图像单帧运动去糊论文 论文地址:【here】 代码地址:【here】 Rethinking Coarse-to-Fine Approach in Single Image Deblurring 引言 图像去糊来自与物体或相机的运动。现有的deblur领域的深度学习方法大多都是coarse-to-fin…...

Mysql 增删改查(二)—— 增(insert)、删(delete)、改(update)
目录 一、插入 1、insert 2、replace(插入否则更新) 二、更新(update) 三、删除 1、delete 2、truncate(截断表,慎用) 一、插入 1、insert (1) 单行 / 多行插入 全列插入:…...

JSD2212复习串讲
1. Java语言基础阶段 这一部分主要是练,给一些题目还有讲解一些最基础的语法,做一些额外的补充 1.1 基本概念 1.2 变量 1.2.1 数据类型 4类8种 基本类型:整形、浮点型、字符型、布尔型 整形:byte -》short-》int-》long 浮点…...

sphinx 升级到6.x后的Jquery问题
sphinx 升级到6.0 后,以前对于jquery的默认引用方式发生了改变以前在编译后的html中jquery是如下引用的:<script src"_static/jquery.js"></script>而升级到6.0后,对于jquery 是一个googleapi的远程jquery调用…...

NSSCTF Round#8 Basic
from:http://v2ish1yan.top MyDoor 使用php伪协议读取index.php的代码 php://filter/readconvert.base64-encode/resourceindex.php<?php error_reporting(0);if (isset($_GET[N_S.S])) {eval($_GET[N_S.S]); }if(!isset($_GET[file])) {header(Location:/index.php?fi…...

多传感器融合定位十二-基于图优化的建图方法其一
多传感器融合定位十二-基于图优化的建图方法其一1. 基于预积分的融合方案流程1.1 优化问题分析1.2 预积分的作用1.3 基于预积分的建图方案流程2. 预积分模型设计3. 预积分在优化中的使用3.1 使用方法3.2 残差设计3.3 残差雅可比的推导3.3.1 姿态残差的雅可比3.3.2 速度残差的雅…...

RockChip MPP编码
概述瑞芯微提供的媒体处理软件平台(Media Process Platform,简称 MPP)是适用于瑞芯微芯片系列的通用媒体处理软件平台。该平台对应用软件屏蔽了芯片相关的复杂底层处理,其目的是为了屏蔽不同芯片的差异,为使用者提供统…...

【学习笔记】NOIP暴零赛2
细思极恐,我的能力已经退步到这个地步了吗? 数据结构 这题的修改是强行加进去迷惑你的。 考虑怎么求树的带权重心。 完了我只会树形dp 完了完了 结论:设uuu的子树和为szusz_uszu,所有点权值和为sss,那么树的带…...

linux基本功系列之hostname实战
文章目录前言一. hostname命令介绍二. 语法格式及常用选项三. 参考案例3.1 显示本机的主机名3.2 临时修改主机名3.3 显示短格式的主机名3.4 显示主机的ip地址四. 永久修改主机名4.1 centos6 修改主机名的方式4.2 centos7中修改主机名永久生效总结前言 大家好,又见面…...
Easy-Es框架实践测试整理 基于ElasticSearch的ORM框架
文章目录介绍(1)Elasticsearch java 客户端种类(2)优势和特性分析(3)性能、安全、拓展、社区(2)ES版本及SpringBoot版本说明索引处理(一)索引别名策略&#x…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
