二叉树题目:完全二叉树插入器
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:完全二叉树插入器
出处:919. 完全二叉树插入器
难度
6 级
题目描述
要求
完全二叉树是每一层(除最后一层外)都是完全填充的,并且所有的结点都尽可能地集中在左侧。
设计一种算法,将一个新结点插入到一个完全二叉树中,并在插入后保持完全二叉树。
实现 CBTInserter \texttt{CBTInserter} CBTInserter 类:
- CBTInserter(TreeNode root) \texttt{CBTInserter(TreeNode root)} CBTInserter(TreeNode root) 使用完全二叉树的根结点 root \texttt{root} root 初始化数据结构;
- int insert(int v) \texttt{int insert(int v)} int insert(int v) 向树中插入一个值为 val \texttt{val} val 的新结点,使树保持完全二叉树的状态,并返回插入结点的父结点的值;
- TreeNode get_root() \texttt{TreeNode get\_root()} TreeNode get_root() 返回树的头结点。
示例
示例 1:

输入:
["CBTInserter", "insert", "insert", "get_root"] \texttt{["CBTInserter", "insert", "insert", "get\_root"]} ["CBTInserter", "insert", "insert", "get_root"]
[[[1, 2]], [3], [4], []] \texttt{[[[1, 2]], [3], [4], []]} [[[1, 2]], [3], [4], []]
输出:
[null, 1, 2, [1, 2, 3, 4]] \texttt{[null, 1, 2, [1, 2, 3, 4]]} [null, 1, 2, [1, 2, 3, 4]]
解释:
CBTInserter cBTInserter = new CBTInserter([1, 2]); \texttt{CBTInserter cBTInserter = new CBTInserter([1, 2]);} CBTInserter cBTInserter = new CBTInserter([1, 2]);
cBTInserter.insert(3); \texttt{cBTInserter.insert(3);} cBTInserter.insert(3); // 返回 1 \texttt{1} 1
cBTInserter.insert(4); \texttt{cBTInserter.insert(4);} cBTInserter.insert(4); // 返回 2 \texttt{2} 2
cBTInserter.get_root(); \texttt{cBTInserter.get\_root();} cBTInserter.get_root(); // 返回 [1, 2, 3, 4] \texttt{[1, 2, 3, 4]} [1, 2, 3, 4]
数据范围
- 树中结点数目在范围 [1, 1000] \texttt{[1, 1000]} [1, 1000] 内
- 0 ≤ Node.val ≤ 5000 \texttt{0} \le \texttt{Node.val} \le \texttt{5000} 0≤Node.val≤5000
- root \texttt{root} root 是完全二叉树
- 0 ≤ val ≤ 5000 \texttt{0} \le \texttt{val} \le \texttt{5000} 0≤val≤5000
- 最多调用 10 4 \texttt{10}^\texttt{4} 104 次 insert \texttt{insert} insert 和 get_root \texttt{get\_root} get_root
解法
思路和算法
这道题的解法不唯一。一种常规的解法是维护完全二叉树中的结点数,每次插入结点时根据结点数定位到插入结点的位置。当完全二叉树中有 n n n 个结点时,该解法每次插入操作的时间复杂度是 O ( log n ) O(\log n) O(logn)。
利用完全二叉树的性质,可以将每次插入操作的时间复杂度降低到 O ( 1 ) O(1) O(1)。
由于完全二叉树的结点插入顺序和层序遍历相同,因此在初始化时可以使用层序遍历访问完全二叉树中的每个结点。每次插入的结点的父结点一定是层序遍历访问到的第一个存在空子结点的结点,父结点满足两个子结点都为空或者只有右子结点为空。如果父结点的两个子结点都为空,则插入的结点作为父结点的左子结点;如果父结点的子结点中只有右子结点为空,则插入的结点作为父结点的右子结点。
如果一个结点的两个子结点都不为空,则下一个插入的结点的父结点一定是层序遍历顺序中当前结点后面的结点。因此,维护完全二叉树的根结点和队列,即可实现每次插入使用 O ( 1 ) O(1) O(1) 的时间完成。
初始化时将根结点入队列,然后执行如下操作:如果队首结点的两个子结点都不为空,则将队首结点出队列,并将队首结点的左子结点和右子结点依次入队列。重复该操作直到队首结点的两个子结点中至少有一个为空。
对于插入结点操作,使用给定的结点值创建新结点,此时队首结点即为插入结点的父结点。执行如下操作。
-
判断父结点的左子结点是否为空,执行相应的操作。
-
如果父结点的左子结点为空,则将新结点作为父结点的左子结点。
-
如果父结点的左子结点不为空,则将新结点作为父结点的右子结点,然后将父结点出队列,并将父结点的左子结点和右子结点依次入队列。
-
-
返回父结点值。
对于返回根结点操作,返回完全二叉树的根结点即可。
代码
class CBTInserter {TreeNode root;Queue<TreeNode> queue;public CBTInserter(TreeNode root) {this.root = root;queue = new ArrayDeque<TreeNode>();queue.offer(root);while (queue.peek().left != null && queue.peek().right != null) {TreeNode node = queue.poll();queue.offer(node.left);queue.offer(node.right);}}public int insert(int val) {TreeNode insertNode = new TreeNode(val);TreeNode node = queue.peek();if (node.left == null) {node.left = insertNode;} else {node.right = insertNode;queue.poll();queue.offer(node.left);queue.offer(node.right);}return node.val;}public TreeNode get_root() {return root;}
}
复杂度分析
-
时间复杂度:构造方法的时间复杂度是 O ( n ) O(n) O(n),插入结点操作和返回根结点操作的时间复杂度都是 O ( 1 ) O(1) O(1),其中 n n n 是二叉树的结点数。构造方法需要对完全二叉树层序遍历,需要 O ( n ) O(n) O(n) 的时间。插入结点操作将新结点作为父结点的子结点,可能有队列操作,需要 O ( 1 ) O(1) O(1) 的时间。返回根结点操作直接返回完全二叉树的根结点,需要 O ( 1 ) O(1) O(1) 的时间。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。需要存储完全二叉树以及使用队列存储完全二叉树中的子结点不完全的结点。
相关文章:

二叉树题目:完全二叉树插入器
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法代码复杂度分析 题目 标题和出处 标题:完全二叉树插入器 出处:919. 完全二叉树插入器 难度 6 级 题目描述 要求 完全二叉树是每一层(除最后一层外)都…...
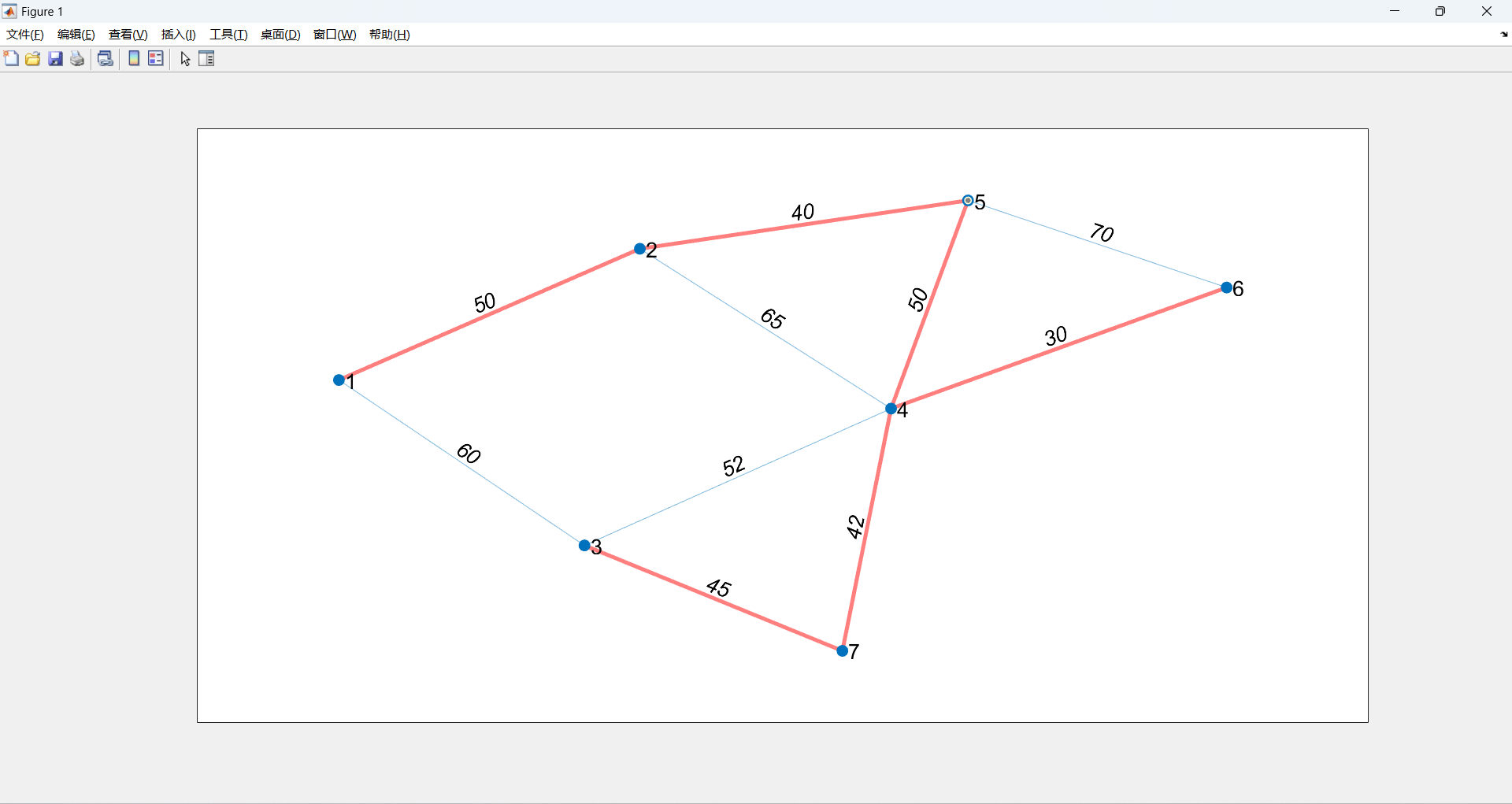
用MATLAB求最短路径(graphshortestpath)和求最小生成树(minspantree),代码演示
求最短路径(graphshortestpath),求最小生成树(minspantree) 文章目录 求最短路径(graphshortestpath),求最小生成树(minspantree)1、最短路径问题2、最小生成…...
用win系统搭建Minecraft世界服务器,MC开服教程,小白开服教程
雨云VPS用Windows系统搭建我的世界世界服务器,Minecraft开服教程,小白开服教程,MC 1.19.4版本服务器搭建教程。 此教程使用 Mohist 1.19.4 服务端,此服务端支持Forge模组和Bukkit/Spigot/Paper插件,如果需要开其他服务…...
MacOS安装Miniforge、Tensorflow、Jupyter Lab等(2024年最新)
大家好,我是邵奈一,一个不务正业的程序猿、正儿八经的斜杠青年。 1、世人称我为:被代码耽误的诗人、没天赋的书法家、五音不全的歌手、专业跑龙套演员、不合格的运动员… 2、这几年,我整理了很多IT技术相关的教程给大家࿰…...
iOS 应用上架指南:资料填写及提交审核
摘要 本文提供了iOS新站上架资料填写及提交审核的详细指南,包括创建应用、资料填写-综合、资料填写-IOS App和提交审核等步骤。通过本指南,您将了解到如何填写正确的资料,并顺利通过苹果公司的审核。 引言 在开发iOS应用后,将其…...
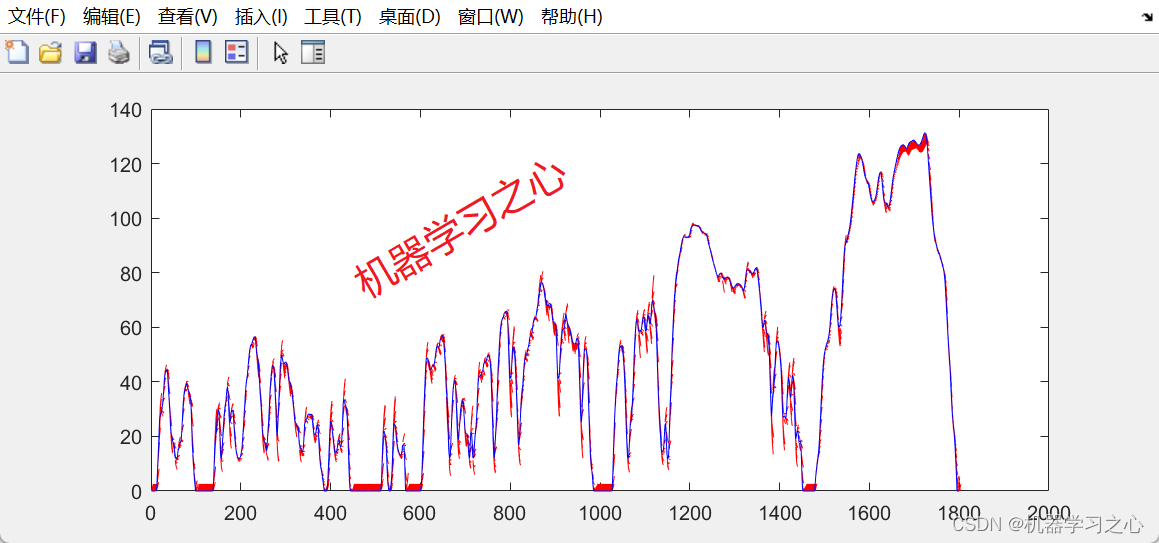
车速预测 | Matlab基于RBF径向基神经网络的车速预测模型(多步预测,尾巴图)
目录 效果一览基本介绍程序设计参考资料 效果一览 基本介绍 车速预测 | Matlab基于RBF径向基神经网络的车速预测模型(多步预测,尾巴图) 程序设计 完整程序和数据获取方式:私信博主回复Matlab基于RBF径向基神经网络的车速预测模型…...
MySQL 5.7.35下载安装使用_忘记密码_远程授权
文章目录 MySQL 5.7.35下载安装使用_忘记密码_远程授权MySQL下载地址mysql安装点击安装,最好以管理员身份运行选择自定义安装选择64位勾选启动自定义产品执行点击同意点击下一步点击执行下一步配置数据库端口号设置登录密码,如果密码忘记,下面…...

openGauss学习笔记-194 openGauss 数据库运维-常见故障定位案例-分析查询语句长时间运行的问题
文章目录 openGauss学习笔记-194 openGauss 数据库运维-常见故障定位案例-分析查询语句长时间运行的问题194.1 分析查询语句长时间运行的问题194.1.1 问题现象194.1.2 原因分析194.1.3 处理办法 openGauss学习笔记-194 openGauss 数据库运维-常见故障定位案例-分析查询语句长时…...

GoLang:gRPC协议的介绍以及详细教程,从Protocol开始
目录 编辑 引言 一、安装相关Go语言库和相关工具 1. 安装Go 2. 安装Protocol Buffers Compiler 2.1 Windows 2.1.1 下载 2.1.2 解压 2.1.3 环境变量 2. macOS 3. Linux 4. 验证安装 3. 安装gRPC-Go 4. 安装Protocol Buffers的Go插件 二、定义服务 三、生成Go…...

LeetCode-2645. 构造有效字符串的最少插入数
给你一个字符串 word ,你可以向其中任何位置插入 “a”、“b” 或 “c” 任意次,返回使 word 有效需要插入的最少字母数。 如果字符串可以由 “abc” 串联多次得到,则认为该字符串有效 。 示例 1: 输入:word “b” …...
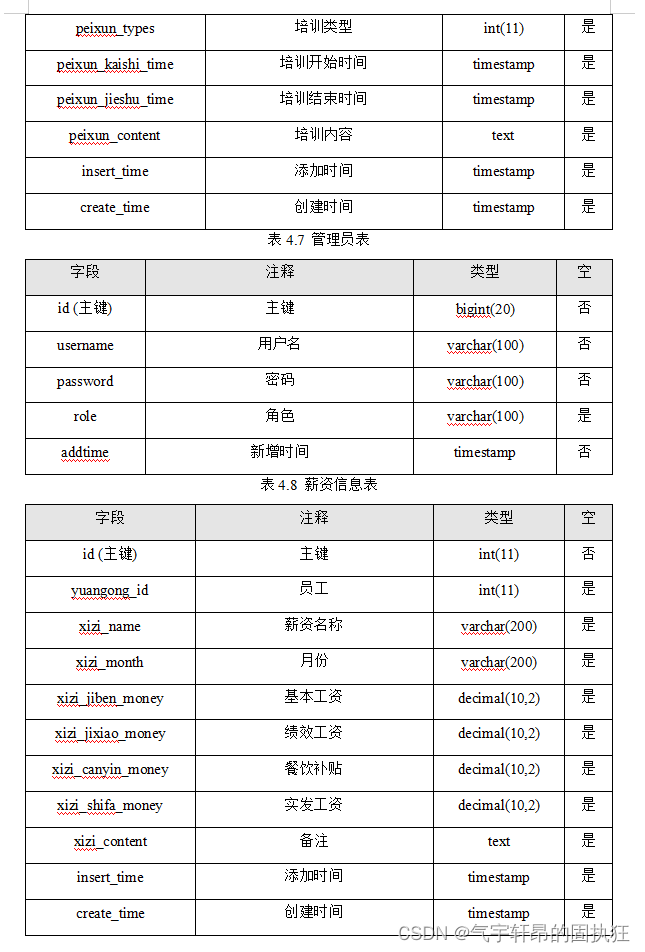
ssm+vue的城投公司企业人事管理系统设计与实现(有报告)。Javaee项目,ssm vue前后端分离项目。
演示视频: ssmvue的城投公司企业人事管理系统设计与实现(有报告)。Javaee项目,ssm vue前后端分离项目。 项目介绍: 采用M(model)V(view)C(controller&#x…...

nginx基础面试题以及配置文件解析和命令控制
目录 1、nginx是什么 2、nginx的特点 3、为什么中国大陆有:百度、京东、新浪、网易、腾讯、淘宝等这么多用户使用nginx 4、nginx 的内部技术架构 上一期我们配置安装了nginx接着讲一下nginx配置文件的解析和nginx 命令控制 感谢观看!希望能够帮助到…...
全自动网页生成系统网站源码重构版
源码优点: 所有模板经过精心审核与修改,完美兼容小屏手机大屏手机,以及各种平板端、电脑端和360浏览器、谷歌浏览器、火狐浏览器等等各大浏览器显示。 免费制作 为用户使用方便考虑,全自动网页制作系统无需繁琐的注册与登入,直…...
【算法每日一练]-动态规划 (保姆级教程 篇16) #纸带 #围栏木桩 #四柱河内塔
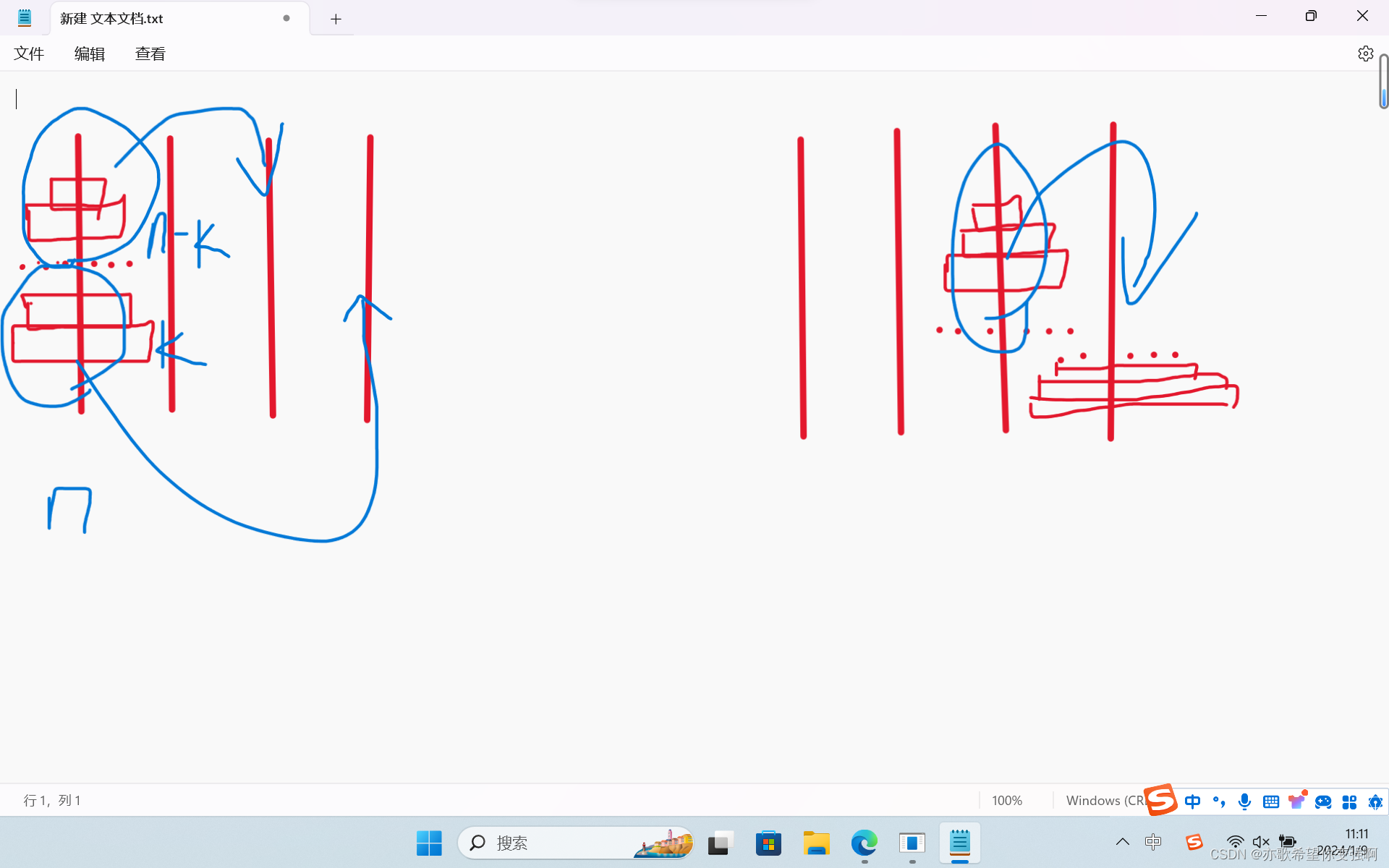
目录 今日知识点: 计算最长子序列的方案个数,类似最短路径个数问题 四柱河内塔问题:dp[i]min{ (p[i-k]f[k])dp[i-k] } 纸带 围栏木桩 四柱河内塔 纸带 思路: 我们先设置dp[i]表示从i到n的方案数。 那么减法操作中ÿ…...

Grounding 模型 + SAM 报错
引入 Grounding 目标检测模型串联 SAM 从而实现实例分割任务,目前支持 Grounding DINO 和 GLIP 参考教程 MMDetection-SAM 如果是 Grounding DINO 则安装如下依赖即可 cd playground pip install githttps://github.com/facebookresearch/segment-anything.git pip…...
linux 网络基础配置
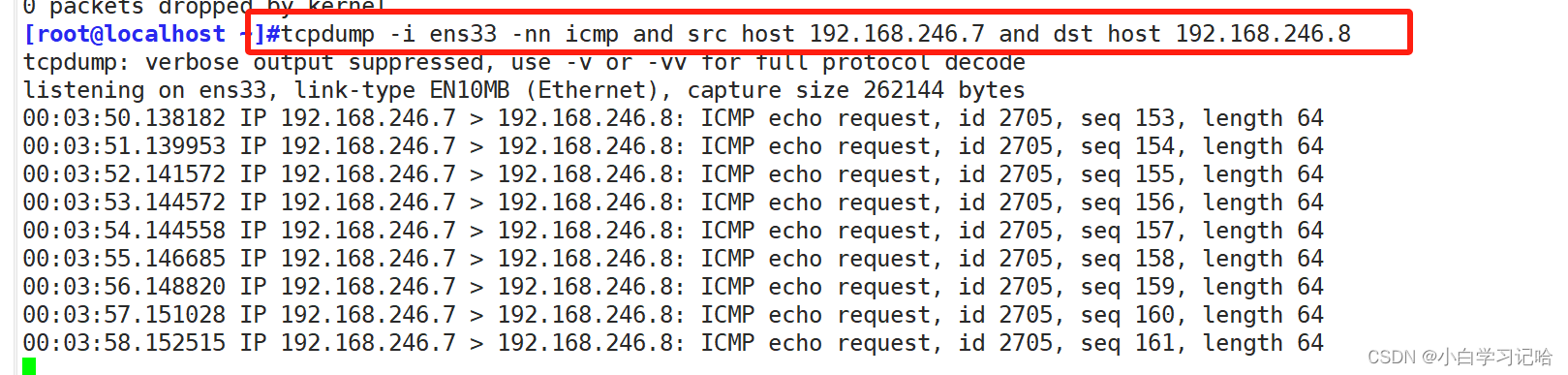
将Linux主机接入到网络,需要配置网络相关设置一般包括如下内容: 主机名 iP/netmask (ip地址,网关) 路由:默认网关 网络连接状态 DNS服务器 (主DNS服务器 次DNS服务器 第三个DNS服务器) 一、…...

leetcode-相同的树
100. 相同的树 使用递归的方法 # Definition for a binary tree node. # class TreeNode: # def __init__(self, val0, leftNone, rightNone): # self.val val # self.left left # self.right right class Solution:def isSameTree(self, p: …...
)
Leetcode17-好数对的数目(1512)
1、题目 给你一个整数数组 nums 。 如果一组数字 (i,j) 满足 nums[i] nums[j] 且 i < j ,就可以认为这是一组 好数对 。 返回好数对的数目。 示例 1: 输入:nums [1,2,3,1,1,3] 输出:4 解释:有 4 组好数对&am…...
Ubuntu22.04开机左上角下划线闪烁不开机
按下CtrlAltF2,打开TTY系统,然后通过用户名和密码登录,随后使用 sudo apt --fix-broken install 根据提示排除错误信息,然后使用apt安装lightdm安装就行。 tips:当使用EasyConnect的时候,你可能参考了下面这篇文章知…...

提升测试多样性,揭秘Pytest插件pytest-randomly
大家可能知道在Pytest测试生态中,插件扮演着不可或缺的角色,为开发者提供了丰富的功能和工具。其中,pytest-randomly 插件以其能够引入随机性的特性而备受欢迎。本文将深入探讨 pytest-randomly 插件的应用,以及如何通过引入随机性…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...

用 FFmpeg 实现 RTMP 推流直播
RTMP(Real-Time Messaging Protocol) 是直播行业中常用的传输协议。 一般来说,直播服务商会给你: ✅ 一个 RTMP 推流地址(你推视频上去) ✅ 一个 HLS 或 FLV 拉流地址(观众观看用)…...
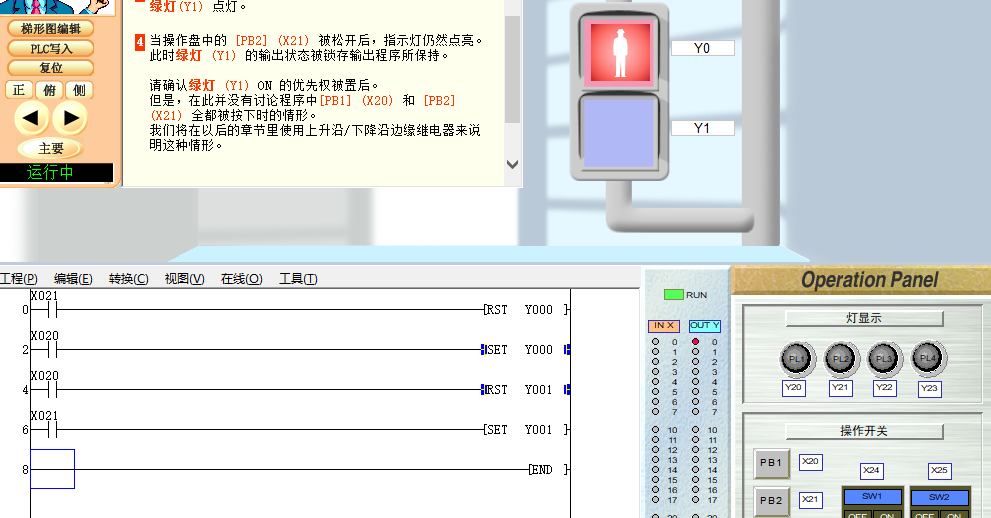
PLC入门【4】基本指令2(SET RST)
04 基本指令2 PLC编程第四课基本指令(2) 1、运用上接课所学的基本指令完成个简单的实例编程。 2、学习SET--置位指令 3、RST--复位指令 打开软件(FX-TRN-BEG-C),从 文件 - 主画面,“B: 让我们学习基本的”- “B-3.控制优先程序”。 点击“梯形图编辑”…...
