揭露欧拉骗局第二篇:逼近公式“Σ1/n=lnn+C”。
Σ1/n=lnn+C是欧拉为调和级数创造(注意是创造、而不是发现)的“逼近公式”,它在欧系大名鼎鼎,因为它解决了欧洲人百筹莫展的“调和级数求和问题”。
“lnn+C”是欧拉的发明,欧拉认为n→∞时,Σ1/n=lnn+常数,这个常数就是欧拉常数C=0.5772156649…。当欧拉发现以10倍率对Σ1/n翻倍分项、分项值会收敛至常数2.30258509、恰恰吻合ln10(其实彼此有差值,但欧拉习惯打马虎眼)以后,他就采用绑架换梁法——用lnn绑架Σ1/n“持续翻倍”、实现lnn替代Σ1/n,从而获得“Σ1/n=lnn+C”,——两个毫无瓜葛的变量因为一个常数变成等量,这个哄鬼瞎话数学人居然都信了!虽然没有任何n值能让Σ1/n=lnn+C成立,但它却成了欧系最著名数学公式之一。欧拉是拿观众当白 痴,诡异的是数学界真的就成了白 痴,没有人指责欧拉胆大妄为,反而都对着鬼话唱赞美歌,他们说n=1.2.3.时不成立,n→∞就成立了。一代代数学人自此面对Σ1/n、在n值“很大的时候(通常>1000000)”就用“lnn+C”顶缸,目前电脑编程采用的就是该方法顶缸,也就是说你求1+1/2+1/3+…+1/2543578618904487,电脑出来的是ln2543578618904487+0.5772156499…。这种恬不知耻的欺诈行为,始作俑者就是欧拉。

欧拉是纯粹数学旗帜,他的谬论构成纯数框架
学过数学的人都知道y=x+C是“平行线(平移函数)”关系,即y是x平移C个点位;C通常是有理数,如果C是无理数,那么y或者x的变量必然都存在取集限制,如此才会产生“无限趋近永不相交”情形。回看Σ1/n=lnn+C,第一眼可得“Σ1/n是lnn平移C个点位”,进一步了解C是无理数,那么Σ1/n与lnn必定是变量受到了取集限制。然而事实不然,Σ1/n与lnn取集完全相同、并无任何限制,故由趋势不可改变理论可以判定:不是平移函数的Σ1/n与lnn必定相交、彼此间不可能存在无理数常量差,也就是说“常数C”是欧拉捏造的,Σ1/n与lnn+C之间绝对画不上等号。
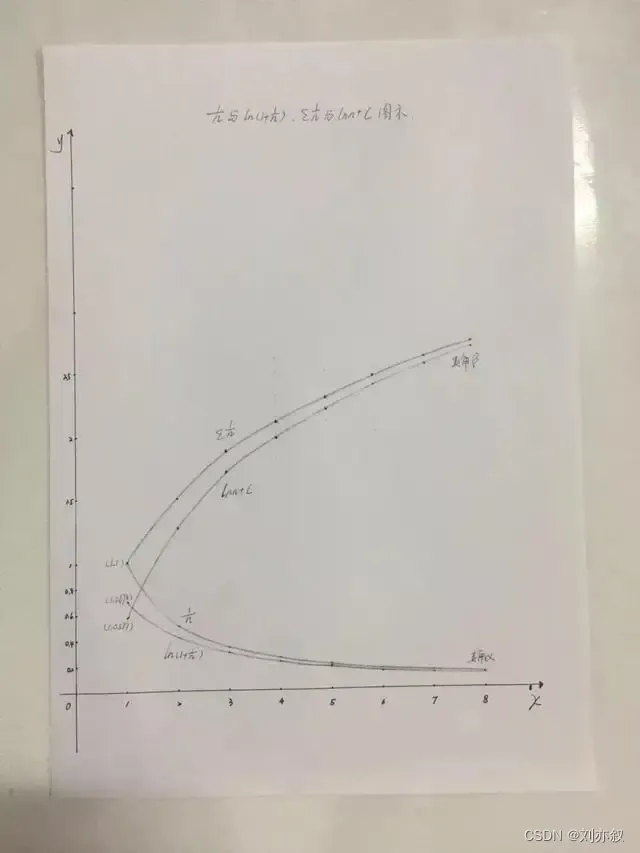 1/n与ln(1+1/n)、Σ1/n与lnn+C趋势必定相交
1/n与ln(1+1/n)、Σ1/n与lnn+C趋势必定相交
再来看Σ1/n、lnn与它们的子项1/n、ln(1+1/n)。Σ1/n是1/n的无限累加,lnn是ln(1+1/n)的无限积分,彼此之间的关系是风马牛毫不相干;1/n→0,ln(1+1/n)→常数,如果Σ1/n>lnn,则0>常数成立,这显然不可能,从这里也能证明Σ1/n=lnn+C荒诞无稽。

没有任何证据能证明Σ1/n=lnn+C成立
Σ1/n=lnn+C从未经过任何证明,它是在欧拉的威名下变成的“公式”的;欧洲人之所以在这个问题上浮皮潦草,一方面是出于对欧拉的忌惮,另一方面是Σ1/n在欧系数学特别重要、但欧洲人长期找不到解决方案,既然Σ1/n=lnn+C能解决Σ1/n问题,大家自然没有二话,也因此李鬼等式及欧拉常数总是被描绘得神秘又高贵、艰涩又诡妙,让数学人的膝盖不由自主地发软。而真实的李鬼等式简单得只需一句话就能概括:用lnn绑架Σ1/n、以x翻倍分级,彼此的差值为欧拉常数,循环论证即为Σ1/n=lnn+C,秘笈只在于用让Σ1/n翻倍分级,使其与k*lnx同步起伏。
戳破欧拉常数和Σ1/n=lnn+C非常简单:画个坐标草图就能发现Σ1/n的收敛速度大过lnn、证明“Σ1/n以x翻倍分项级数=lnx”不成立;使用最简单的硬算法,至迟n=9890128,lnn+C就会上穿Σ1/n、令“欧拉常数”破产、令李鬼等式现形(有兴趣者可以实算验证,只要是硬算而不是编程,分分钟可以证明欧拉造假作弊)。
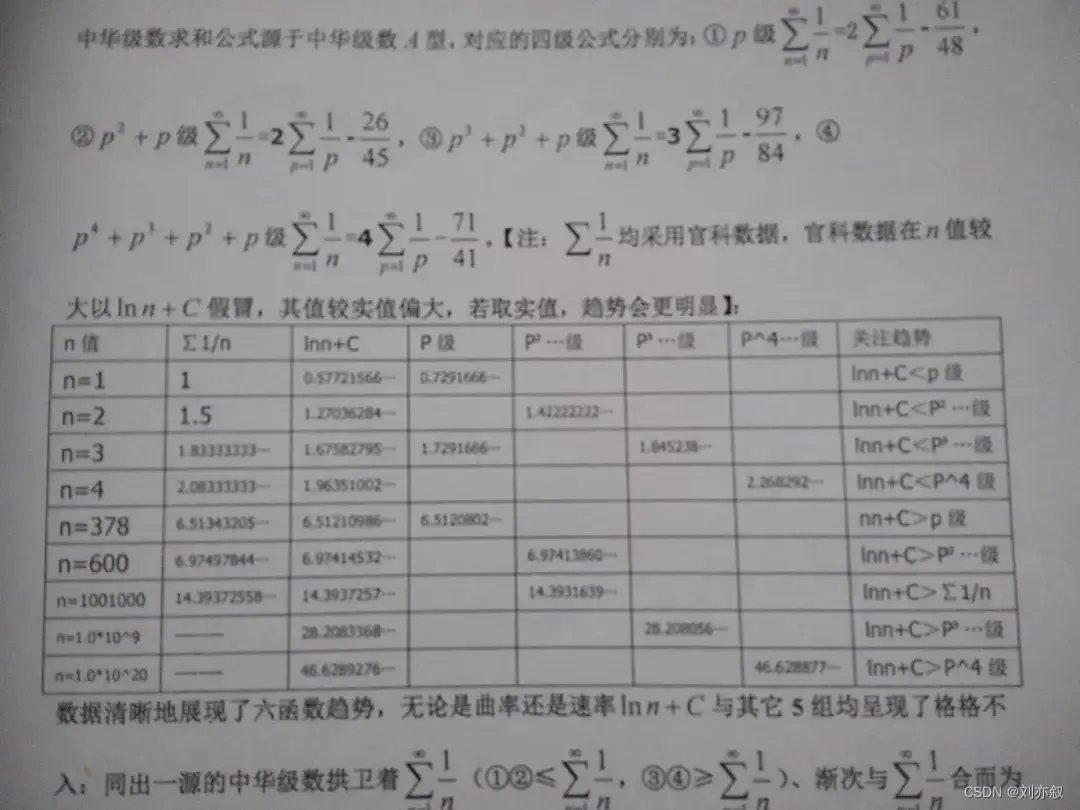 Σ1/n有多种直算方法
Σ1/n有多种直算方法
李鬼等式Σ1/n=lnn+C能在数学界堂而皇之,仰仗的除了欧拉的大名,还有它的无从证伪,它让人类数学走了几百年弯路,空耗了人类的无限才智带来的却全是负能量。
邀你讨论

欧拉常数公式的证明很难
吗?说说你的看法
去发布
相关文章:

揭露欧拉骗局第二篇:逼近公式“Σ1/n=lnn+C”。
Σ1/nlnnC是欧拉为调和级数创造(注意是创造、而不是发现)的“逼近公式”,它在欧系大名鼎鼎,因为它解决了欧洲人百筹莫展的“调和级数求和问题”。 “lnnC”是欧拉的发明,欧拉认为n→∞时,Σ1/nlnn常数,这个常数就是欧…...

MYSQL的学习——单行函数详解
目录 1. 数值函数 1) 基本函数 2) 角度与弧度互换函数 3) 三角函数 4) 指数与对数函数 5) 进制间的转换 2. 字符串函数 3. 日期和时间函数 1) 获取日期、时间 2) 日期与时间戳的转换 3) 获取月份、星期、星期数、天数等函数 4) 日期的操作函数 5) 时间和秒钟转换的…...

深度解析Cron表达式:精确控制任务调度的艺术
深度解析Cron表达式:精确控制任务调度的艺术 希望我们都可以满怀期待的路过每一个转角 去遇见 那个属于自己故事的开始 去追寻那个最真实的自己 去放下 去拿起 安然,自得,不受世俗牵绊… 导言 在计算机科学领域,任务调度是一项关…...

java实现AES256对称加解密工具类
一、引入依赖包 引入相关依赖包 <dependency><groupId>org.bouncycastle</groupId><artifactId>bcprov-jdk15on</artifactId><version>1.70</version> </dependency> <!--lombok用于简化实体类开发--> <dependency&g…...
其他排序(基数排序,希尔排序和桶排序)(数据结构课设篇3,python版)(排序综合)
本篇博客主要详细讲解一下其他排序(基数排序,希尔排序和桶排序)也是排序综合系列里最后一篇博客。第一篇博客讲解的是LowB三人组(冒泡排序,插入排序,选择排序)(数据结构课设篇1&…...

【复现】DiffTalk
code:GitHub - sstzal/DiffTalk: [CVPR2023] The implementation for "DiffTalk: Crafting Diffusion Models for Generalized Audio-Driven Portraits Animation" 问题1. ERROR: Failed building wheel for pysptk Cython.Compiler.Errors.CompileError:…...

SQLServer 系统概述
目录 1.SQL语言的发展和特点 2.SQL语言的特点 1.SQL语言的发展和特点 SQL是利用一些简单的语句构成的基本语法,来存储数据库的内容。目前已经成为关系型数据库系统中使用最广泛的语言。 1974年SQL语言由Boyce和Chamberlin提出来。 1975~1979年研制了著名的关系数…...

Vue3 + TS + Element-Plus —— 项目系统中封装表格+搜索表单 十分钟写五个UI不在是问题
前期回顾 纯前端 —— 200行JS代码、实现导出Excel、支持DIY样式,纵横合并-CSDN博客https://blog.csdn.net/m0_57904695/article/details/135537511?spm1001.2014.3001.5501 目录 一、🛠️ newTable.vue 封装Table 二、🚩 newForm.vue …...

Linux系统——测试端口连通性方法
目录 一、TCP端口连通性测试 1、ssh 2、telnet(可能需要安装) 3、curl 4、tcping(需要安装) 5、nc(需要安装) 6、nmap(需要安装) 二、UDP端口连通性测试 1、nc(…...

Python虚拟环境轻松配置:Jupyter Notebook中的内核管理指南
问题 在Python开发中,一些人在服务器上使用Jupyter Notebook中进行开发。一般是创建虚拟环境后,向Jupyter notebook中添加虚拟环境中的Kernel,后续新建Notebook中在该Kernel中进行开发,这里记录一下如何创建Python虚拟环境以及添…...
大数据-hive函数与mysql函数的辨析及练习-将多行聚合成一行
目录 1. 🥙collect_list: 聚合-不去重 2. 🥙collect_set(col): 聚合-去重 3. 🥙mysql的聚合函数-group_concat 4. leetcode练习题 1. 🥙collect_list: 聚合-不去重 将组内的元素收集成数组 不会去重 2. 🥙collec…...

【AI视野·今日NLP 自然语言处理论文速览 第七十三期】Tue, 9 Jan 2024
AI视野今日CS.NLP 自然语言处理论文速览 Tue, 9 Jan 2024 Totally 80 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers FFSplit: Split Feed-Forward Network For Optimizing Accuracy-Efficiency Trade-off in Language Model Infe…...

vue知识-03
购物车案例 要实现的功能: 1、计算商品总价格 2、全选框和取消全选框 3、商品数量的增加和减少 <body> <div id"app"><div class"row"><div class"col-md-6 col-md-offset-3"><h1 class"text-center…...

关于httpClient 使用的注意事项
关于httpClient 使用的注意事项 用例 PoolingHttpClientConnectionManager connectionManager new PoolingHttpClientConnectionManager();// 最大连接数-不设置默认20connectionManager.setMaxTotal(200);// 每个路由最大连接数-不设置默认2connectionManager.setDefaultMax…...
Docker 发布自定义镜像到公共仓库
Docker 发布自定义镜像到公共仓库 引言 Docker 是一种轻量级、便携式的容器化技术,可以使应用程序在不同环境中更加可移植。在本文中,我们将学习如何使用 Docker 从公共仓库拉取 Nginx 镜像,定制该镜像,添加自定义配置文件&…...

程序员有哪些接单的渠道?
这题我会!程序员接单的渠道那可太多了,想要接到合适的单子,筛选一个合适的平台很重要。如果你也在寻找一个合适的接单渠道,可以参考以下这些方向。 首先,程序员要对接单有一个基本的概念:接单渠道可以先粗略…...
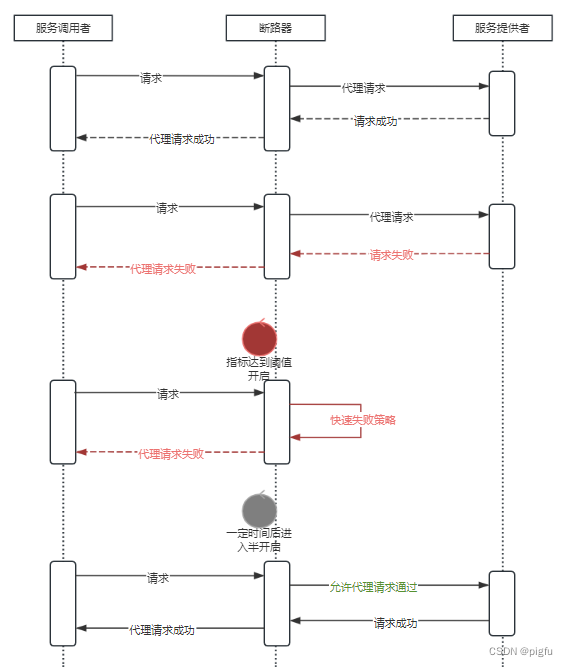
服务容错-熔断策略之断路器hystrix-go
文章目录 概要一、服务熔断二、断路器模式三、hystrix-go3.1、使用3.2、源码 四、参考 概要 微服务先行者Martin Fowler与James Lewis在文章microservices中指出了微服务的九大特征,其中一个便是容错性设计(Design for failure)。正如文章中提到的,微服…...
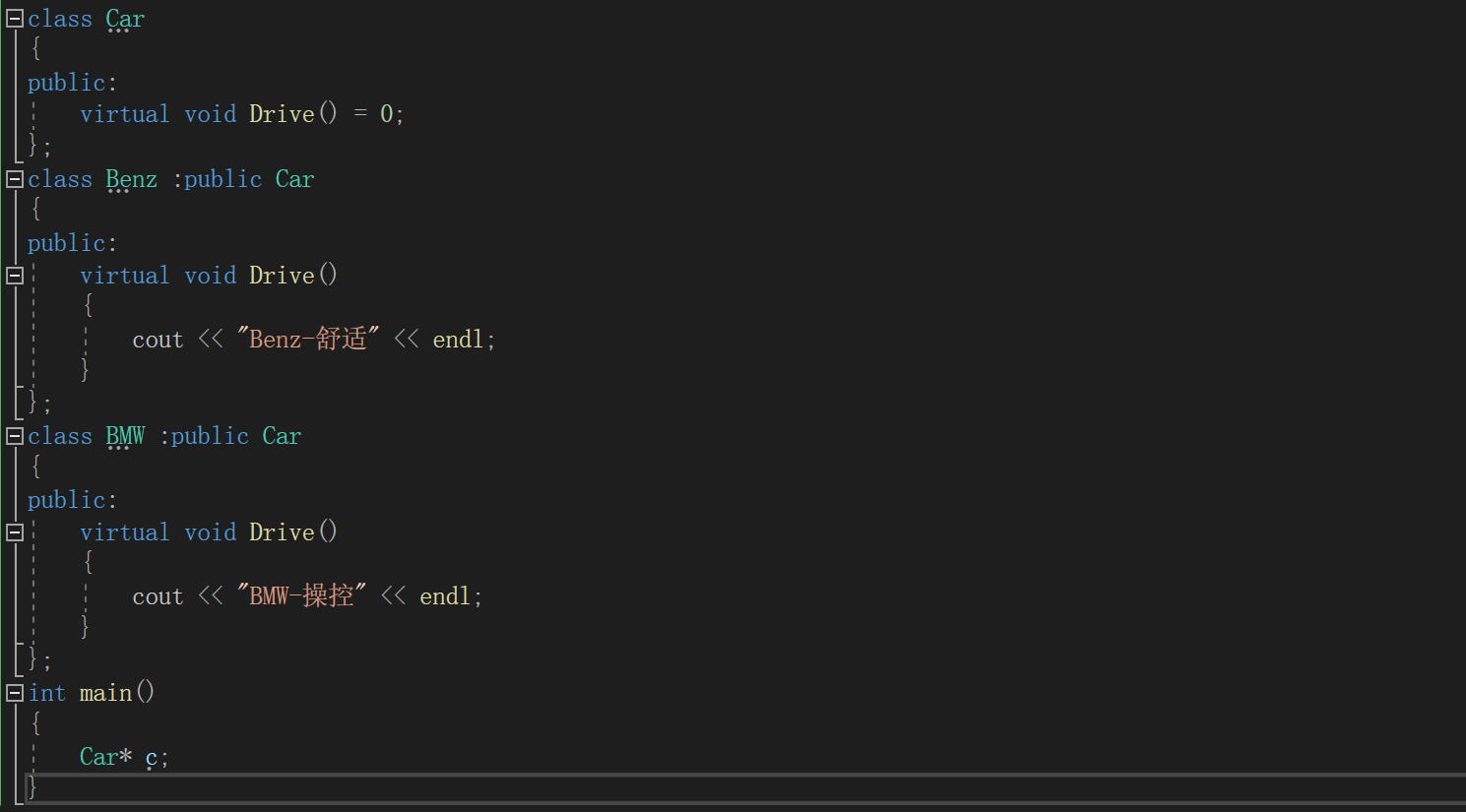
C++进阶(三)多态
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、多态的概念1、概念 二、多态的定义及实现1、多态的构成条件2、虚函数3、虚函数的重写4、C…...

大众汽车宣布将ChatGPT,批量集成在多种汽车中!
1月9日,大众汽车在官网宣布,将ChatGPT批量集成到电动、内燃机汽车中。 大众表示,将ChatGPT与其IDA语音助手相结合,用户通过自然语言就能与ChatGPT进行互动,例如,帮我看看最近的三星米其林饭店在哪里&#…...

React----函数组件和类组件
函数组件与类组件:React 中的两种组件风格 React 是一个用于构建用户界面的流行 JavaScript 库,其中组件是构建块的基本单元。在 React 中,有两种主要的组件风格:函数组件和类组件。本文将使用TypeScript介绍它们的用法、区别以及…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...
