2024美赛数学建模思路 - 复盘：光照强度计算的优化模型

0 赛题思路

（赛题出来以后第一时间在CSDN分享）

https://blog.csdn.net/dc_sinor?type=blog

1 问题要求

现在已知一个教室长为15米，宽为12米，在距离地面高2.5米的位置均
匀的安放4个光源（分别为1、2、3、4），各个光源的光照强度均为一个单位，如下图

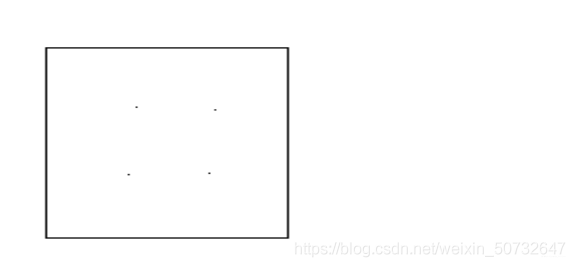
要求：

• （1）如何计算教室内任意一点的光照强度？（光源对目标点的光照强度与该光源到目标点距离的平方成反比，与该光源的强度成正比）.
• （2）画出距离地面1米处各个点的光照强度与位置（横纵坐标）之间的函数关系曲面图，试同时给出一个近似的函数关系式.
• （3）假设离地面1米高正是学生桌面的高度，如何设计这四个点光源的位置，才能使学生对光照的平均满意度达到最高？
• （4）若将题目中的点光源换成线光源，以上(2)、(3)问的结果又如何？

（对于（1）、（2）问，假设横向（纵向）墙壁与光源、光源与光源、光源与墙壁之间的距离是相等的.）

2 假设约定

• 1 光不会通过窗、门等外涉，也不考虑光在空气中的消耗，即光照强度和不变；
• 2 室内不受外界光源影响；
• 3 教室高度为2.5米；
• 4 不考虑光的反射；
• 5 线光源发光是均匀的.

3 符号约定

4 建立模型

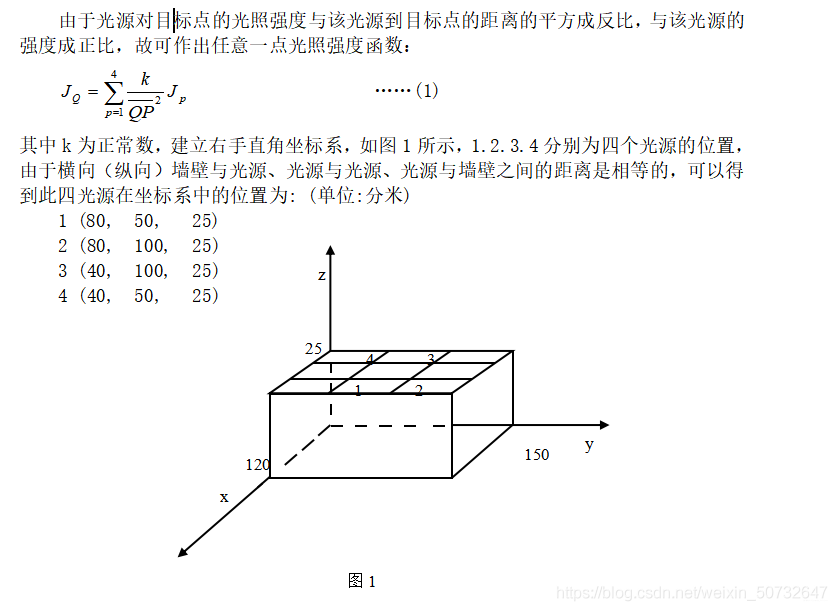
5 模型求解

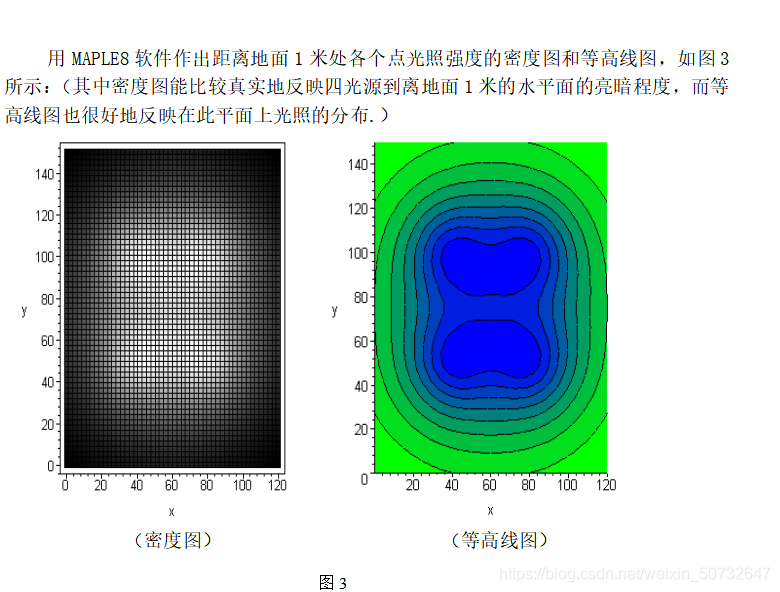
6 实现代码

matlab 实现代码
建议最好用python去实现，图会好看一些，而且国内当前趋势会逐渐淘汰matlab，目前有些学校已经无法使用matlab了

clear
clc
max=0;min=4;
for i=0:0.1:3for j=0.1:0.1:4s=0;x1=8+i,y1=5-jx2=8+i,y2=10+jx3=4-i,y3=10+jx4=4-i,y4=5-j     for x=0:0.1:12for y=0:0.1:15for z=0:0.1:2.5if x1~=x & y1~=y & x2~=x & y2~=y & x3~=x & y3~=y & x4~=x & y4~=y s=s+1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1./((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2);endendendendk=4./s;l=0;z=1;for x=0:0.1:12for y=0:0.1:15l=l+k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1/((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2));endendif l>maxmax=l;x11=x1;y11=y1;x12=x2;y12=y2;x13=x3;y13=y3;x14=x4;y14=y4;endp=l./(120.*150);Q=0;for x=0:0.1:12for y=0:0.1:15Q=Q+(k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1./((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2))-p).^2.^(1./2);endendif min>Qmin=Q;x21=x1;y21=y1;x22=x2;y22=y2;x23=x3;y23=y3;x24=x4;y24=y4;endend
end
disp(['最大值','x11=',num2str(x11),'  ','y11=',num2str(y11),'  ','x12=',num2str(x12),'  ','y12=',num2str(y12),'  ','x13=',num2str(x13),'  ','y13=',num2str(y13),'  ','x14=',num2str(x14),'  ','y14=',num2str(y14)])
disp(['最平均','x21=',num2str(x21),'  ','y21=',num2str(y21),'  ','x22=',num2str(x22),'  ','y22=',num2str(y22),'  ','x23=',num2str(x23),'  ','y23=',num2str(y23),'  ','x24=',num2str(x24),'  ','y24=',num2str(y24)])
附录二：
clear
clc
max=0;min=4;li=4;
for i=0:0.1:3for j=0.1:0.1:4s=0;x1=8+i,y1=5-jx2=8+i,y2=10+jx3=4-i,y3=10+jx4=4-i,y4=5-j     for x=0:0.1:12for y=0:0.1:15for z=0:0.1:2.5if x1~=x & y1~=y & x2~=x & y2~=y & x3~=x & y3~=y & x4~=x & y4~=y s=s+1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1./((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2);endendendendk=4./s;l=0;z=1;e=0for x=0:0.1:12for y=0:0.1:15l=l+k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1/((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2));r=k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1/((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2));e=e+(r-6*10^(-32))^2;endendS=(l-0.1278)^2+eif S<lili=Sx11=x1,y11=y1,  x12=x2,y12=y2,  x13=x3,y13=y3,  x14=x4,y14=y4,en4en4
en4
disp(['x11=',num2str(x11),'  ','y11=',num2str(y11),'  ','x12=',num2str(x12),'  ','y12=',num2str(y12),'  ','x13=',num2str(x13),'  ','y13=',num2str(y13),'  ','x14=',num2str(x14),'  ','y14=',num2str(y14)])
li

建模资料

资料分享: 最强建模资料