扩散模型(二)——DDIM学习笔记-大白话推导
扩散模型系列:
(1)扩散模型(一)——DDPM推导笔记-大白话推导
(2)扩散模型(二)——DDIM学习笔记-大白话推导
请提前关注,后续待更新,谢谢…
写在前面:
(1)建议看这篇论文之前,可先看我写的前一篇论文:
扩散模型(一)——DDPM推导笔记-大白话推导
主要学习和参考了以下文章:
(1)一文带你看懂DDPM和DDIM
(2)关于 DDIM 采样算法的推导
0. DDIM的创新点
DDPM有一个很大的缺点就是其本身是一个马尔科夫链的过程,推理速度太慢,如果前向加噪过程是1000步,那么去噪过程就需要使用Unet生成噪声,然后去噪,这样进行1000步。这是一个及其缓慢的过程,DDIM原论文中举了一个生动的例子:
For example, it takes around 20 hours to sample 50k images of size 32 x 32 from a DDPM, but less than a minute to do so from a GAN on a Nvidia 2080 Ti GPU.
基于DDPM,DDIM主要有两项改进:
(1)对于一个已经训练好的DDPM,只需要对采样公式做简单的修改,模型就能在去噪时「跳步骤」,在一步去噪迭代中直接预测若干次去噪后的结果。比如说,假设模型从时刻T=100开始去噪,新的模型可以在每步去噪迭代中预测10次去噪操作后的结果,也就是逐步预测时刻t=90,80,…,0的结果。这样,DDPM的采样速度就被加速了10倍。
(2)DDIM论文推广了DDPM的数学模型,打破了马尔科夫链的过程,从更高的视角定义了DDPM的反向过程(去噪过程)。在这个新数学模型下,我们可以自定义模型的噪声强度,让同一个训练好的DDPM有不同的采样效果。
1. 公式推导
DDPM的推导过程可以看《DDPM推导笔记》,这里假设 P ( x t − 1 ∣ x t , x 0 ) P(x_{t-1}|x_t, x_0) P(xt−1∣xt,x0)满足如下正态分布,即:
P ( x t − 1 ∣ x t , x 0 ) ∼ N ( k x 0 + m x t , σ 2 ) 即 : x t − 1 = k x o + m x t + σ ϵ 其中有: ϵ ∼ N ( 0 , 1 ) (1) P(x_{t-1}|x_t, x_0) \sim N(kx_0+mx_t, \sigma^2) \\ 即:x_{t-1} = kx_o+mx_t + \sigma \epsilon \tag{1} \\ 其中有: \epsilon \sim N(0, 1) P(xt−1∣xt,x0)∼N(kx0+mxt,σ2)即:xt−1=kxo+mxt+σϵ其中有:ϵ∼N(0,1)(1)
又因为前向的加噪过程满足:
x t = a t ˉ x 0 + 1 − a t ˉ ϵ 其中 ϵ ∼ N ( 0 , 1 ) (2) x_t = \sqrt{\bar{a_t}} x_0 + \sqrt{1 - \bar{a_t}} \epsilon \\ 其中\epsilon \sim N(0,1) \tag{2} xt=atˉx0+1−atˉϵ其中ϵ∼N(0,1)(2)
合并(1)(2)上面两式,有:
x t − 1 = k x 0 + m [ a ˉ t x 0 + 1 − a ˉ t ϵ ] + σ ϵ (3) x_{t-1} = kx_0 + m[\sqrt{\bar{a}_t}x_0 + \sqrt{1-\bar{a}_t} \epsilon] + \sigma \epsilon \tag{3} xt−1=kx0+m[aˉtx0+1−aˉtϵ]+σϵ(3)
再次合并有:
x t − 1 = ( k + m a ˉ t ) x 0 + ϵ ′ 其中: ϵ ’ ∼ M ( 0 , m 2 ( 1 − a ˉ t ) + σ 2 ) (4) x_{t-1} = (k+m\sqrt{\bar{a}_t}) x_0 + \epsilon' \\ 其中: \epsilon’ \sim M(0, m^2(1-\bar{a}_t) + \sigma^2) \tag{4} xt−1=(k+maˉt)x0+ϵ′其中:ϵ’∼M(0,m2(1−aˉt)+σ2)(4)
从DDPM中可以可知:
x t − 1 = a ˉ t − 1 x 0 + 1 − a ˉ t − 1 ϵ (5) x_{t-1} = \sqrt{\bar{a}_{t-1}} x_0 + \sqrt{1-\bar{a}_{t-1}} \epsilon \tag{5} xt−1=aˉt−1x0+1−aˉt−1ϵ(5)
通过式(4)(5)的 x t − 1 x_{t-1} xt−1服从的概率分布可知:
k + m a ˉ t = a ˉ t − 1 m 2 ( 1 − a ˉ t ) + σ 2 = 1 − a ˉ t − 1 (6) k + m\sqrt{\bar{a}_t} = \sqrt{\bar{a}_{t-1}} \\ m^2(1-\bar{a}_t) + \sigma^2 = 1-\bar{a}_{t-1} \tag{6} k+maˉt=aˉt−1m2(1−aˉt)+σ2=1−aˉt−1(6)
由式(6)两个式子可解出:
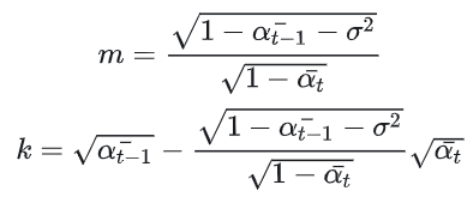
将m,k带入到 P ( x t − 1 ∣ x t , x 0 ) P(x_{t-1}|x_t, x_0) P(xt−1∣xt,x0)中,可得:
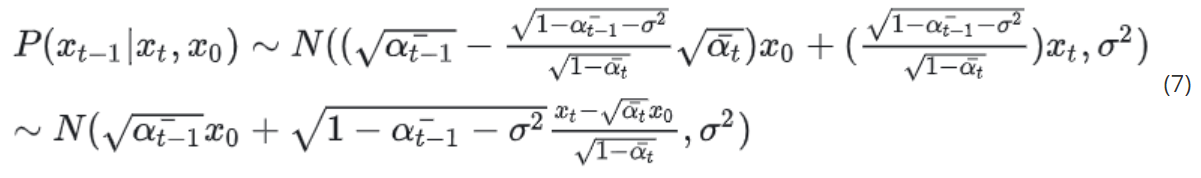
依旧可以使用 x t , x 0 x_t, x_0 xt,x0的关系式把 x 0 x_0 x0去掉:
x t = a t ˉ x 0 + 1 − a t ˉ ϵ 这里为了防止 ϵ 和后面的 ϵ 搞混,这里记为 ϵ t , 则上式变为: x t = a t ˉ x 0 + 1 − a t ˉ ϵ t (8) x_t = \sqrt{\bar{a_t}} x_0 + \sqrt{1 - \bar{a_t}} \epsilon \\ 这里为了防止\epsilon和后面的\epsilon搞混,这里记为\epsilon_{t},则上式变为:\\ x_t = \sqrt{\bar{a_t}} x_0 + \sqrt{1 - \bar{a_t}} \epsilon_t \tag{8} xt=atˉx0+1−atˉϵ这里为了防止ϵ和后面的ϵ搞混,这里记为ϵt,则上式变为:xt=atˉx0+1−atˉϵt(8)
从 P ( x t − 1 ∣ x t , x 0 ) P(x_{t-1}|x_t, x_0) P(xt−1∣xt,x0)的概率分布采样可得到:
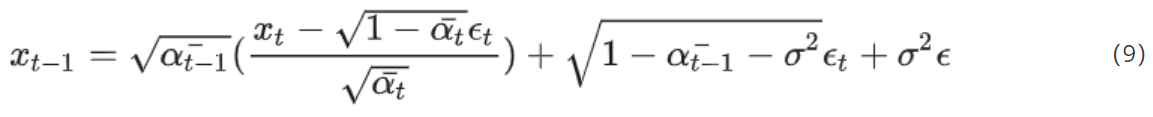
其中, ϵ \epsilon ϵ是从标准正太分布中,随机采样得到; ϵ t \epsilon_t ϵt是和DDPM一样,使用神经网络训练而来的; x t x_t xt是输入; a ˉ t − 1 和 a ˉ t \bar{a}_{t-1}和\bar{a}_t aˉt−1和aˉt是事先定义好的。至此,我们就只需要讨论 σ \sigma σ这个参数了。
2. σ \sigma σ的讨论
怎样选取 σ \sigma σ才能获得最佳的加速效果呢?
作者做了一些实验,作者原文中使用 σ τ i ( η ) \sigma_{\tau_i}{(\eta)} στi(η)来表示的 σ \sigma σ,其式子如下:
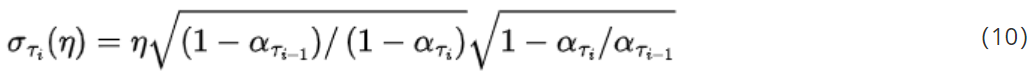
使用 η \eta η控制其大小。事实上,当 η = 1 \eta = 1 η=1时就变成了DDPM的去噪过程了,
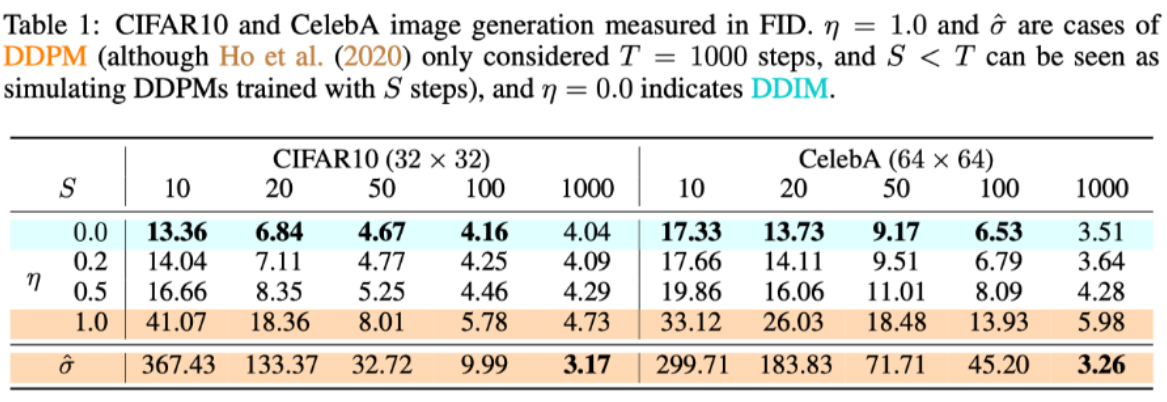
当 η = 0 \eta=0 η=0时,效果是最好的。所以DDIM令 σ = 0 \sigma=0 σ=0。
3. x p r e v x_{prev} xprev的推导
从式9且 σ = 0 \sigma=0 σ=0,则式9中的所有都已知了!!!
但是,即使这样,我们也还是由 x t 推导出 x t − 1 x_t推导出x_{t-1} xt推导出xt−1呀,这样还是不能加快推理!
不忙,我们回过头去思考,发现上面的推导过程中全程没有使用:
x t = a t x t − 1 + 1 − a t ϵ x_t= \sqrt{a_t}x_{t-1} + \sqrt{1-a_t} \epsilon xt=atxt−1+1−atϵ
也就可以不需要严格的由 x t 算到 x t − 1 x_t算到x_{t-1} xt算到xt−1,则可以令 x p r e v 替代 x t − 1 x_{prev}替代x_{t-1} xprev替代xt−1,式(9)则可以变换为:
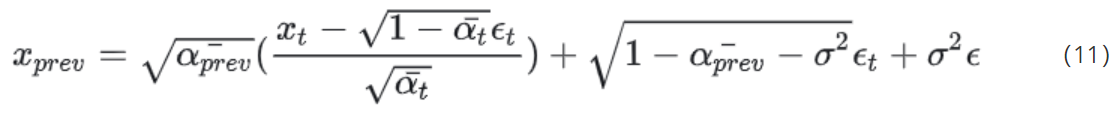
至此,所有的参数要是实现定义好了,要么是需要训练的,这样 x t 和 x p r e v x_t和x_{prev} xt和xprev则可以相隔多个迭代步数。
4.疑难解答
Q1: 为什么式(11)可以简单的将 x p r e v 替代 x t − 1 x_{prev}替代x_{t-1} xprev替代xt−1,毕竟虽然反向过程没有使用到 x t − 1 算到 x t x_{t-1}算到x_{t} xt−1算到xt的关系式,但前向过程是使用到的呀?
目前我也没有答案!还在理解中,由大佬路过,请留言讨论!
Q2: 为什么在DDIM可以令方差 σ = 0 \sigma=0 σ=0 ?
目前我也没有答案!还在理解中,由大佬路过,请留言讨论!
相关文章:
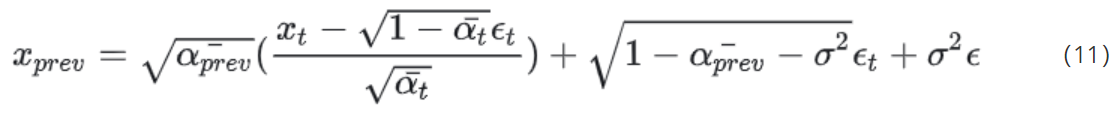
扩散模型(二)——DDIM学习笔记-大白话推导
扩散模型系列: (1)扩散模型(一)——DDPM推导笔记-大白话推导 (2)扩散模型(二)——DDIM学习笔记-大白话推导 请提前关注,后续待更新,谢谢… 写在前面: (1)建议…...
【软件测试作业_TPshop商城】农业工程学院-测试需求分析与测试计划+自动化+性能+测试用例+报告软件缺陷+测试计划+单元测试+系统测试
1测试需求分析与测试计划 1.1 被测系统简介 1.2测试需求分析 1.2.1单元测试层面的测试需求分析 1.2.2系统测试层面的测试需求分析 1.3测试计划 1.31测试范围与任务 1.3.2 测试环境 1.3.3测试进度安排 测试用例的设计2 2.1单元测试层面的测试用例设计 2.2系统测试层面的测试用例…...
屏幕截图编辑工具Snagit中文
Snagit是一款优秀的屏幕、文本和视频捕获与转换程序。它能够捕获屏幕、窗口、客户区窗口、最后一个激活的窗口或用鼠标定义的区域,并支持BMP、PCX、TIF、GIF或JPEG格式的保存。Snagit还具有自动缩放、颜色减少、单色转换、抖动等功能,并能将捕获的图像转…...
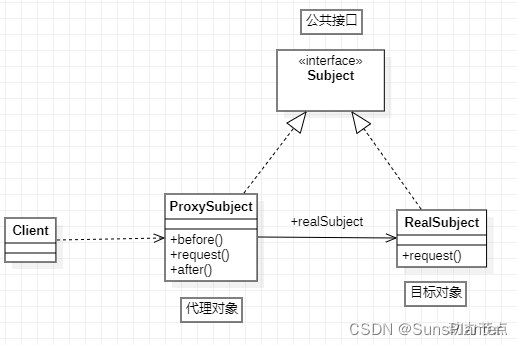
12GoF之代理模式
解决问题的思维:AOP 解决问题技术:代理技术 代理技术太麻烦,因此使用框架 Spring AOP框架(底层是代理技术:jdk动态daili,cglib) 代理模式是GoF23种设计模式之一。属于结构型设计模式。 代理…...

Unity中URP下实现能量罩(扭曲流光花纹)
文章目录 前言一、能量罩花纹1、在属性面板接收能量罩花纹纹理2、申明 纹理 和 采样器3、在顶点着色器,应用 Tilling 和 Offset4、在片元着色器,纹理采样后,与之前的结果相乘输出 二、能量罩流光1、在顶点着色器,记录原uv值2、在片…...

南京银行高管上新:“70后董事长”谢宁将上任,能否及时救场?
撰稿|行星 来源|贝多财经 2024年上市银行的首例“换帅”事件,由南京银行拉开帷幕。 1月8日,南京银行(SH:601009)发布公告称,该行2024年第一次临时股东大会选举产生了第十届董事会11名董事,同意选举谢宁担…...

K8S容器编排基本使用
Kubernetes容器编排技术基本使用 1.部署模式发展历程 物理单机 – 虚拟机(VMware)-- IAAS(基础设施即服务 比如够买jsp主机模式)-- OPENSTACK(多个机器分片使用思想)-- docker(容器化…...

PyTorch 各种池化层函数全览与用法演示
目录 torch.nn.functional子模块Pooling层详解 avg_pool1d 用法与用途 参数 注意事项 示例代码 avg_pool2d 用法与用途 参数 注意事项 示例代码 avg_pool3d 用法与用途 参数 注意事项 示例代码 max_pool1d 用法与用途 参数 注意事项 示例代码 max_pool2d…...
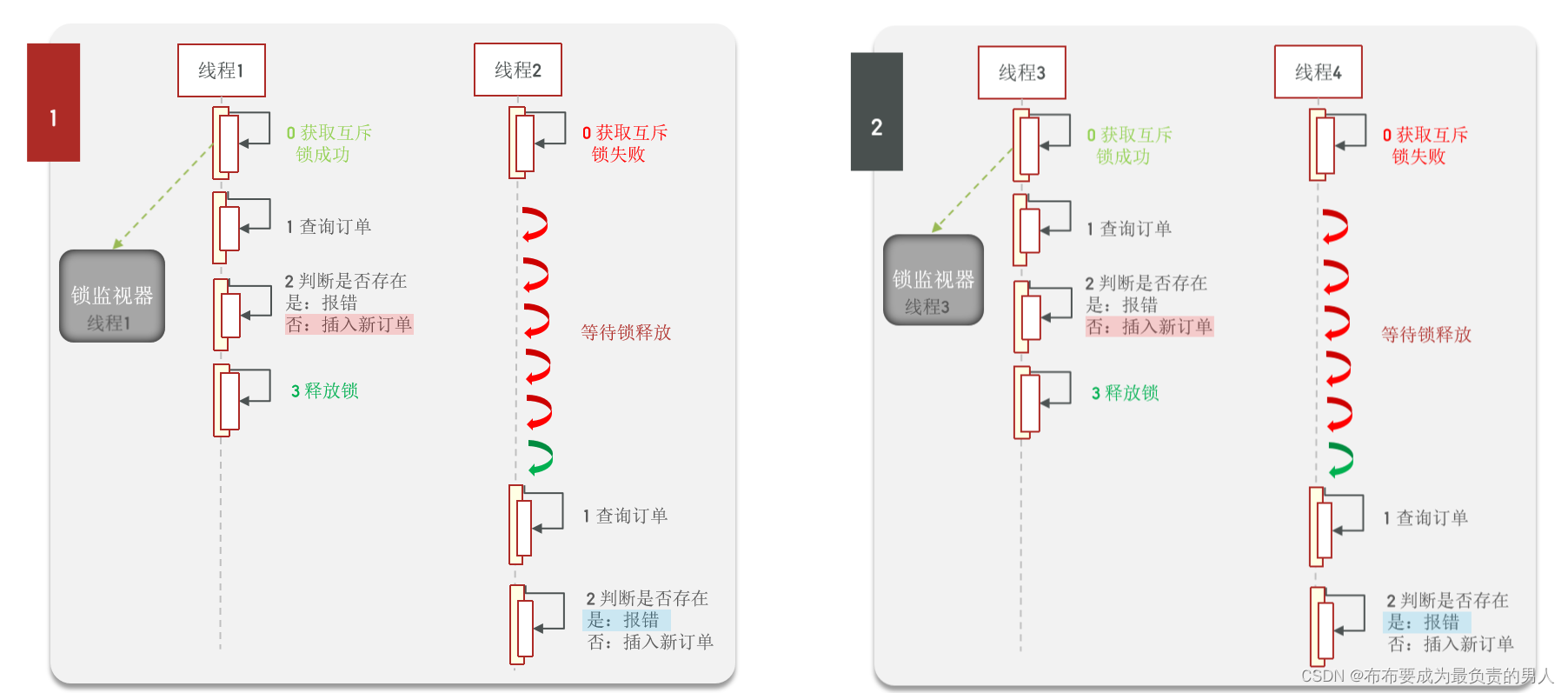
Redis:原理速成+项目实战——Redis实战7(优惠券秒杀+细节解决超卖、一人一单问题)
👨🎓作者简介:一位大四、研0学生,正在努力准备大四暑假的实习 🌌上期文章:Redis:原理速成项目实战——Redis实战6(封装缓存工具(高级写法)&&缓存总…...

【刷题笔记3】
笔记3 输出小数位数控制。(自动四舍五入,不够就自动补0) double a123.456; cout<<fixed<<setprecision(2)<<a;递归题目的记录 (1):n*m的棋盘格子(n为横向的格子数…...

YOLOv8优化策略:轻量化改进 | 华为Ghostnet,超越谷歌MobileNet | CVPR2020
🚀🚀🚀本文改进:Ghost bottleneck为堆叠Ghost模块 ,与YOLOV8建立轻量C2f_GhostBottleneck 🚀🚀🚀YOLOv8改进专栏:http://t.csdnimg.cn/hGhVK 学姐带你学习YOLOv8,从入门到创新,轻轻松松搞定科研; 1.Ghostnet介绍 论文: https://arxiv.org/pdf/1911.11907.…...

格雷希尔G65系列快速接头满足汽车减震器的气压、油压测试要求
当汽车经过不平路面时,汽车减震器可以抑制弹簧吸震后因反弹带来的震荡和来自路面的冲击,为乘客带来平稳舒适的行车体验。减震器在出厂之前,需要模拟汽车的真实行驶环境,在模拟当中需要对它们进行气压和油压的轮番测试。 客户的测试…...

php中常用的几个安全函数
1. mysql_real_escape_string() 这个函数对于在PHP中防止SQL注入攻击很有帮助,它对特殊的字符,像单引号和双引号,加上了“反斜杠”,确保用户的输入在用它去查询以前已经是安全的了。但你要注意你是在连接着数据库的情况下使用这个…...
【K8S 云原生】Kurbernets集群的调度策略
目录 一、Kubernetes的list-watch机制 1、List-watch 2、创建pod的过程: 二、scheduler调度的过程和策略: 1、简介 2、预算策略:predicate 3、优先策略: 3.1、leastrequestedpriority: 3.2、balanceresourceal…...
预览的vue组件库)
vue-office 支持多种文件(docx、excel、pdf)预览的vue组件库
一、文档链接 https://gitcode.com/mirrors/501351981/vue-office/overview?utm_sourcecsdn_github_accelerator&isLogin1 二、安装 #docx文档预览组件 npm install vue-office/docx vue-demi0.13.11#excel文档预览组件 npm install vue-office/excel vue-demi0.13.11#…...

如何使用GaussDB创建脱敏策略(MASKING POLICY)
目录 一、前言 二、GaussDB中的脱敏策略 1、数据脱敏的定义 2、创建脱敏策略的语法说明 三、在GaussDB中如何创建数据脱敏策略(示例) 1、创建脱敏策略的一般步骤 2、GaussDB数据库中创建脱敏策略的完整示例 1)开启安全策略开关,以初识用户omm登录…...

【Golang map并发报错】panic: assignment to entry in nil map
go并发写map[string]interface{}数据的时候,报错:panic: assignment to entry in nil map 多个key同时操作一个map时,如: test[key1] 1 test[key2] "a" test[key3] true 就会遇到并发nil值报错,什么…...
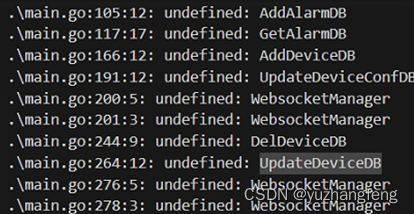
【GO语言依赖】Go语言依赖管理简述
在运行环境中,遭遇报错,显示找不到函数 经过研究后发现需要进行依赖管理,进行如下操作后解决: 起源 最早的时候,Go所依赖的所有的第三方库都放在GOPATH这个目录下面。这就导致了同一个库只能保存一个版本的代码。如…...

论文阅读记录SuMa SuMa++
首先是关于SuMa的阅读,SuMa是一个完整的激光SLAM框架,核心在于“基于面元(surfel)”的过程,利用3d点云转换出来的深度图和法向量图来作为输入进行SLAM的过程,此外还改进了后端回环检测的过程,利用提出的面元的概念和使…...
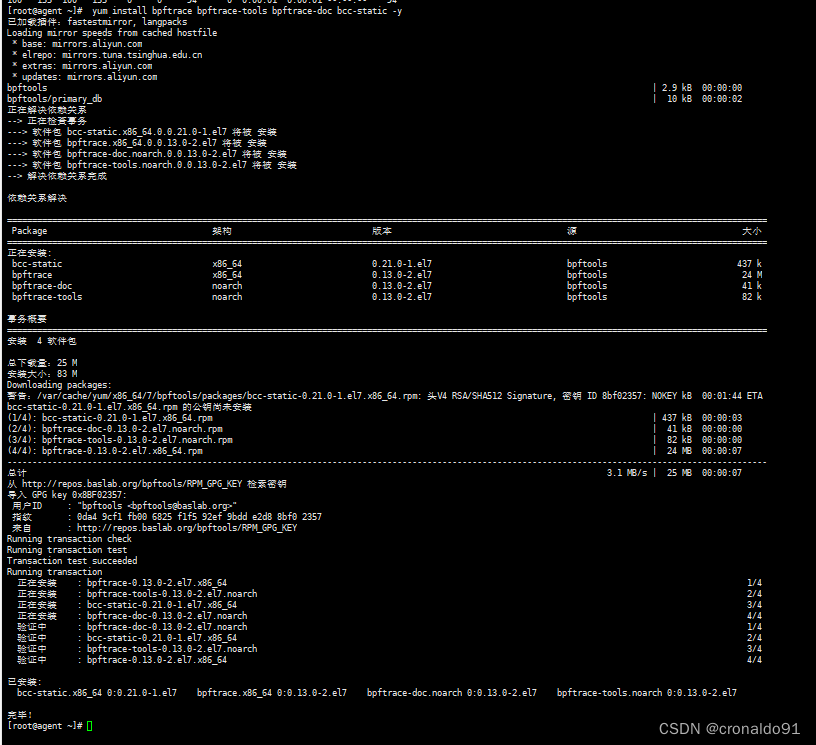
性能分析与调优: Linux 内存观测工具
目录 一、实验 1.环境 2.vmstat 3.PSI 4.swapon 5.sar 6.slabtop 7.numstat 8.ps 9.top 10.pmap 11.perf 12.bpftrace 二、问题 1.接口读写报错 2.slabtop如何安装 3.numactl如何安装 4.numad启动服务与关闭NUMA 5. perf如何安装 6. kernel-lt-doc与kern…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
