约数个数和约数之和算法总结
知识概览
约数个数
基于算数基本定理,假设N分解质因数的结果为
可得对于N的任何一个约数d,有
因为N的每一个约数和
~
的一种选法是一一对应的,根据乘法原理可得,
一个数的约数个数为
约数之和
一个数的约数之和公式为
多项式乘积的每一项为
正好对应的是一个数的每一个约数。
例题展示
约数个数
题目链接
活动 - AcWing系统讲解常用算法与数据结构,给出相应代码模板,并会布置、讲解相应的基础算法题目。![]() https://www.acwing.com/problem/content/872/
https://www.acwing.com/problem/content/872/
代码
#include <iostream>
#include <algorithm>
#include <unordered_map>using namespace std;typedef long long LL;const int mod = 1e9 + 7;int main()
{int n;cin >> n;unordered_map<int, int> primes;while (n--){int x;cin >> x;for (int i = 2; i <= x / i; i++)while (x % i == 0){x /= i;primes[i]++;}if (x > 1) primes[x]++;}LL res = 1;for (auto prime : primes) res = res * (prime.second + 1) % mod;cout << res << endl;return 0;
}约数之和
题目链接
活动 - AcWing系统讲解常用算法与数据结构,给出相应代码模板,并会布置、讲解相应的基础算法题目。![]() https://www.acwing.com/problem/content/873/
https://www.acwing.com/problem/content/873/
代码
#include <iostream>
#include <algorithm>
#include <unordered_map>using namespace std;typedef long long LL;const int mod = 1e9 + 7;int main()
{int n;cin >> n;unordered_map<int, int> primes;while (n--){int x;cin >> x;for (int i = 2; i <= x / i; i++)while (x % i == 0){x /= i;primes[i]++;}if (x > 1) primes[x]++;}LL res = 1;for (auto prime : primes){int p = prime.first, a = prime.second;LL t = 1;while (a--) t = (t * p + 1) % mod;res = res * t % mod;}cout << res << endl;return 0;
}参考资料
- AcWing算法基础课
相关文章:
约数个数和约数之和算法总结
知识概览 约数个数 基于算数基本定理,假设N分解质因数的结果为 可得对于N的任何一个约数d,有 因为N的每一个约数和~的一种选法是一一对应的,根据乘法原理可得, 一个数的约数个数为 约数之和 一个数的约数之和公式为 多项式乘积的…...
数据结构-怀化学院期末题(322)
图的深度优先搜索 题目描述: 图的深度优先搜索类似于树的先根遍历,是树的先根遍历的推广。即从某个结点开始,先访问该结点,然后深度访问该结点的第一棵子树,依次为第二顶子树。如此进行下去,直到所有的结点…...

小手也能用的高性能鼠标,自定义空间还挺高,雷柏VT9Pro mini上手
今年搭载PAW3395传感器的电竞鼠标很受欢迎,雷柏就出了不少型号,满足各种喜好的玩家选择,像是近期新出的搭载3395高定版的VT9Pro和VT9Pro mini,就在轻量化的基础上,满足了各种手型的玩家的使用需要,而且价格…...
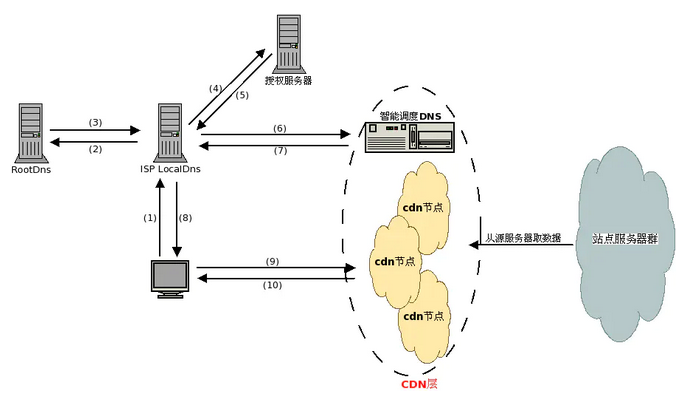
CDN加速原理详解
一、CDN加速是什么意思 CDN是Content Delivery Network)英文首字母的缩写,中文翻译为内容分发网络,由于CDN是为加快网络访问速度而被优化的网络覆盖层,因此被形象地称为”网络加速器”,即CDN加速。CDN加速是通过将网站…...

sqlachemy orm create or delete table
sqlacehmy one to one ------detial to descript 关于uselist的使用。如果你使用orm直接创建表关系,实际上在数据库中是可以创建成多对多的关系,如果加上uselistFalse 你会发现你的orm只能查询出来一个,如果不要这个参数orm查询的就是多个,一对多的…...
科普小米手机、华为手机、红米手机、oppo手机、vivo手机、荣耀手机、一加手机、realme手机如何设置充电提示音
用空空鱼就可以设置,上面还有很多提示音素材还可以设置满电和低电提醒...
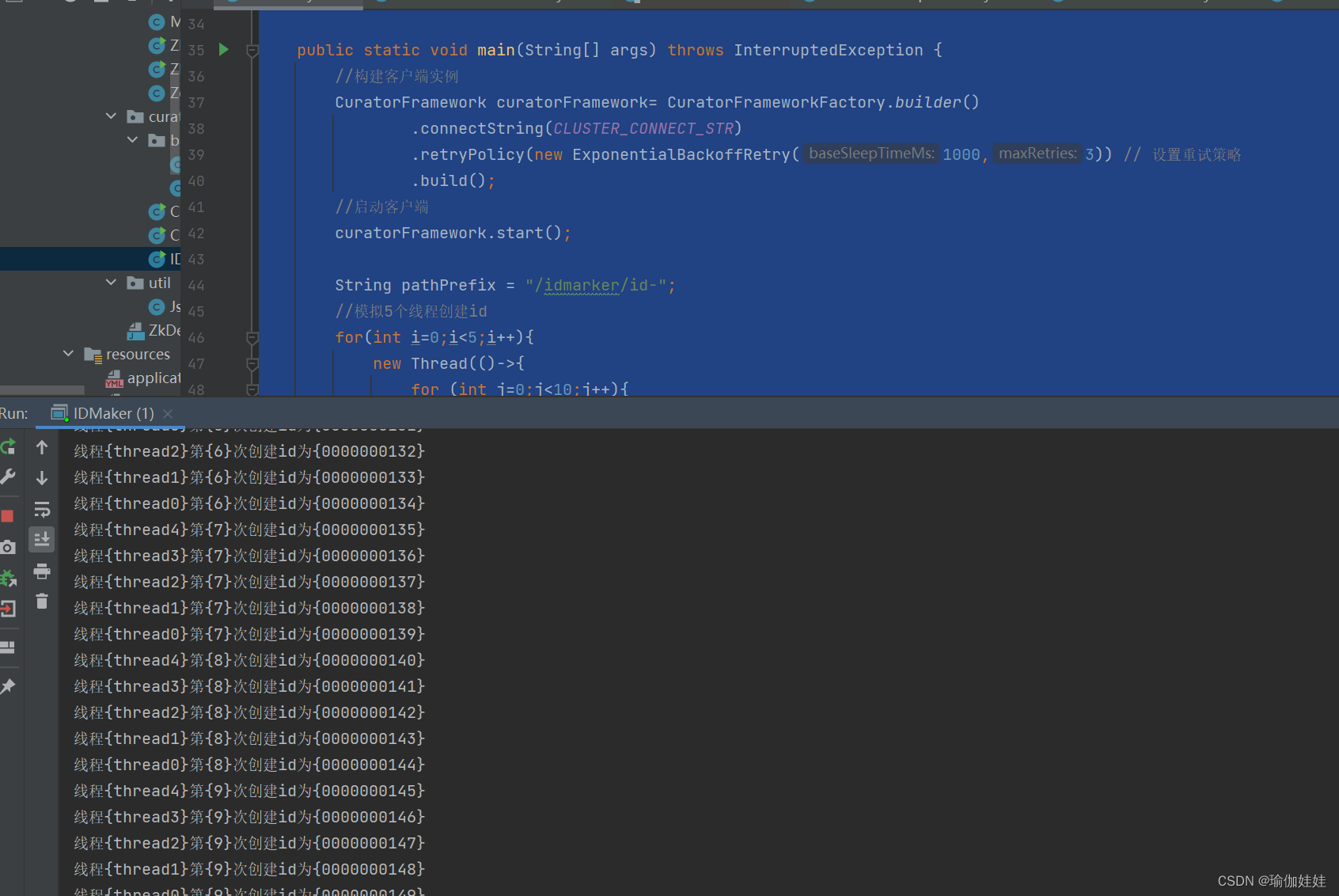
zookeeper应用场景之分布式的ID生成器
1. 分布式ID生成器的使用场景 在分布式系统中,分布式ID生成器的使用场景非常之多: 大量的数据记录,需要分布式ID。大量的系统消息,需要分布式ID。大量的请求日志,如restful的操作记录,需要唯一标识&#x…...
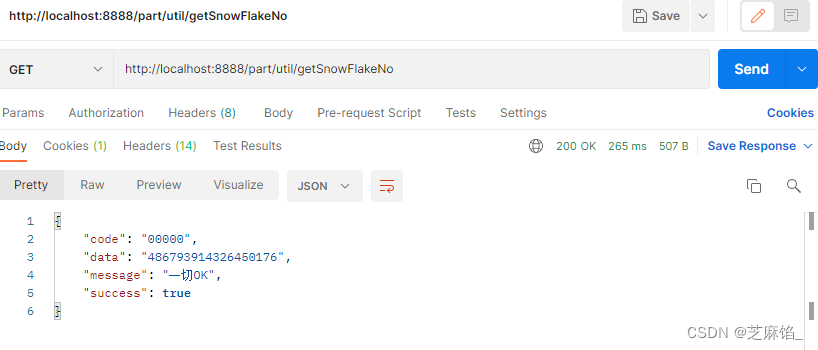
Java--Spring项目生成雪花算法数字(Twitter SnowFlake)
文章目录 前言步骤查看结果 前言 分布式系统常需要全局唯一的数字作为id,且该id要求有序,twitter的SnowFlake解决了这种需求,生成了符合条件的这种数字,本文将提供一个接口获取雪花算法数字。以下为代码。 步骤 SnowFlakeUtils …...

紫光展锐M6780丨画质增强——更炫的视觉体验
智能显示被认为是推动数字化转型和创新的重要技术之一。研究机构数据显示,预计到2035年底,全球智能显示市场规模将达到1368.6亿美元,2023-2035年符合年增长率为36.4%。 随着消费者对高品质视觉体验的需求不断增加,智能手机、平板…...

控制el-table的列显示隐藏
控制el-table的列显示隐藏,一般的话可以通过循环来实现,但是假如业务及页面比较复杂的话,list数组循环并不好用。 在我们的页面中el-table-column是固定的,因为现在是对现有的进行维护和迭代更新。 对需要控制列显示隐藏的页面进…...

2024上海国际冶金及材料分析测试仪器设备展览会
2024上海国际冶金及材料分析测试仪器设备展览会 时间:2024年12月18~20日 地点:上海新国际博览中心 ◆ 》》》组织机构: 主办单位:全联冶金商会、中国宝武钢铁集团有限公司、上海市金属学会 支持单位ÿ…...

商业定位,1元平价商业咨询:豪威尔咨询!平价咨询。
在做生意之前,就需要对企业整体进行一完整的商业定位,才能让商业定位带动企业进行飞速发展。 所以,包含商业定位的有效工作内容就显得极为重要,今天,小编特地为大家整理出了商业定位所需要的筹备的工作,如下…...
2. Presto应用
该笔记来源于网络,仅用于搜索学习,不保证所有内容正确。文章目录 1、Presto安装使用2、事件分析3、漏斗分析4、漏斗分析UDAF开发开发UDF插件开发UDAF插件 5、漏斗测试 1、Presto安装使用 参考官方文档:https://prestodb.io/docs/current/ P…...

工业级安卓PDA超高频读写器手持掌上电脑,RFID电子标签读写器
掌上电脑,又称为PDA。工业级PDA的特点就是坚固,耐用,可以用在很多环境比较恶劣的地方。 随着技术的不断发展,加快了数字化发展趋势,RFID技术就是RFID射频识别及技术,作为一种新兴的非接触式的自动识别技术&…...

Prompt提示工程上手指南:基础原理及实践(一)
想象一下,你在装饰房间。你可以选择一套标准的家具,这是快捷且方便的方式,但可能无法完全符合你的个人风格或需求。另一方面,你也可以选择定制家具,选择特定的颜色、材料和设计,以确保每件家具都符合你的喜…...

Redis如何保证缓存和数据库一致性?
背景 现在我们在面向增删改查开发时,数据库数据量大时或者对响应要求较快,我们就需要用到Redis来拿取数据。 Redis:是一种高性能的内存数据库,它将数据以键值对的形式存储在内存中,具有读写速度快、支持多种数据类型…...

学完C/C++,再学Python是一种什么体验?
你好,我是安然无虞。 文章目录 变量及类型变量类型动态类型特性 注释输入输出通过控制台输出通过控制台输入 运算符算术运算符关系运算符逻辑运算符赋值运算符 条件循环语句条件语句语法格式代码案例缩进和代码块空语句pass 循环语句while循环语法格式代码案例 for…...
ssm基于Java的壁纸网站设计与实现论文
目 录 目 录 I 摘 要 III ABSTRACT IV 1 绪论 1 1.1 课题背景 1 1.2 研究现状 1 1.3 研究内容 2 2 系统开发环境 3 2.1 vue技术 3 2.2 JAVA技术 3 2.3 MYSQL数据库 3 2.4 B/S结构 4 2.5 SSM框架技术 4 3 系统分析 5 3.1 可行性分析 5 3.1.1 技术可行性 5 3.1.2 操作可行性 5 3…...

零基础也可以探索 PyTorch 中的上采样与下采样技术
目录 torch.nn子模块Vision Layers详解 nn.PixelShuffle 用法与用途 使用技巧 注意事项 参数 示例代码 nn.PixelUnshuffle 用法与用途 使用技巧 注意事项 参数 示例代码 nn.Upsample 用法与用途 使用技巧 注意事项 参数 示例代码 nn.UpsamplingNearest2d …...

代码随想录算法训练营Day23|669. 修剪二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树
目录 669. 修剪二叉搜索树 前言 思路 递归法 108.将有序数组转换为二叉搜索树 前言 递归法 538.把二叉搜索树转换为累加树 前言 递归法 总结 669. 修剪二叉搜索树 题目链接 文章链接 前言 本题承接昨天二叉搜索树的插入和删除操作题目,要对整棵二叉搜索树…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
