数据结构——第三章 栈与队列(2)
栈的运用
- 1.括号匹配
- 2.表达式求值
- 2.1.算术表示式的形式
- 2.2.后缀表达式求值
- 2.3.将算术表达式转换为后缀表达式
- 2.4.算术表达式直接求值
- 3.栈与递归
- 3.1.递归算法
- 3.2.栈与函数调用
- 3.3.递归工作与递归函数
- 3.4.递归到非递归的转换
1.括号匹配
void matching(char str[])
{//创建空栈LinkStack S;S = NULL;int k;int flag = 1;char e;for (k = 0; str[k] != '\0'; k++){if (str[k] != '(' && str[k] != ')' && str[k] != '[' && str[k] != ']' && str[k] != '{' && str[k] != '}'){//非括号处理continue;}switch (str[k])//对括号进行匹配处理{case '(':case '{':case '['://遇到左括号进栈PushLinkStack(&S, str[k]);break;case ')'://遇到右圆括号if (S != NULL){GetTopStack(S, &e);if (e == '('){PopLinkStack(&S, &e);//栈顶是左圆括号,匹配成功}else{flag = 0;//栈顶不是左圆括号,匹配失败}}else{flag = 0;//栈空,匹配失败}break;case ']'://遇到右方括号if (S != NULL){GetTopStack(S, &e);if (e == '['){PopLinkStack(&S, &e);//栈顶是左方括号,匹配成功}else{flag = 0;//栈顶不是左方括号,匹配失败}}else{flag = 0;//栈空,匹配失败}break;case '}'://遇右花括号if (S != NULL){GetTopStack(S, &e);if (e == '}'){PopLinkStack(&S, &e);//栈顶是左右花括号,匹配成功}else{flag = 0;//栈顶不是左右花括号,匹配失败}}else{flag = 0;//栈空,匹配失败}break; }//switch}//forif (flag == 1 && S == NULL){printf("括号匹配!\n");}else{printf("括号不匹配!\n");}
}
2.表达式求值
C语言有着丰富的表示式,那么C的编译器是如何处理表达式的呢?
2.1.算术表示式的形式
数学上的算法表达式通常包括操作数和运算符。
- 操作数:简单变量或表达式,用s1,s2表示。
- 运算符:+、-,*,/,(,),用op表示。
通常的算术表达形式即为数学表达式形式,如3*(5-2)+7。由于运算符的优先级,因此求值不一定能够按照从左向右的顺序执行。如果能将算术表示式转成易于从左向右的顺序执行,即可大大提高计算机的执行效率。
算术表达式除了数学上的表达形式外,还有如下三种表达形式。
(1)中缀表达式(运算符位于两个操作数之间):s1 op s2
(2)前缀表达式(运算符位于两个操作数之前): op s1 s2
(3)后缀表达式(运算符位于两个操作数之后): s1 s2 op
以算术表达式 3*(5-2)+7为例,下面给出算术表达形式的步骤。依次处理算术表达式中级别较低的运算符,为了从形式上明确运算符的两个操作对象,约定当操作对象是表达式时,用一对花括号括起来,结果如下。
- 中缀表达式的处理顺序。
①处理‘+’:{3 * (5-2)} + 7; ②处理‘ * ’:3 * {5-2} +7; ③处理‘-’:3 * 5-2+7 - 前缀表达式的处理顺序。
①处理‘+’:+{3 * (5-2)}7;②处理‘ * ’:+ * 3{(5-2)}7;③处理‘-’:+ * 3-527 - 后缀表达式的处理顺序。
①处理‘+’:{3 * (5-2)}7+;②处理‘ * ’:3{(5-2)} * 7+;③处理‘-’:352 - * 7+
不难看出:三种表达式的操作数顺序相同,但运算符顺序不一。其中,中缀表达式丢失了算术表达式中的括号信息,致使运算符的运算顺序不能确定,计算会出现二义性;前缀表达式的运算规则是连续出现的两个操作数和在它们之前且紧靠它们的运算符构成一个最小的表达式,由于运算符的顺序与计算机算顺序不一致,因此需要多次扫描前缀式,才能得到表达式的计算,效率低;后缀表达式中的运算规则是连续出现两个操作数和在它们之后紧靠它们的运算符构成一个最小的表达式,由于运算符的顺序与计算机顺序一致,因此只需一次扫描后缀式,即可完成表达式的计算,效率高。
2.2.后缀表达式求值
求值过程:后缀表达式是一个字符串,为了方便处理,以‘#’结束。用一个栈(假定数据元素类型为整型)来存放操作数和中间计算结果。对后缀表达式从左向右依次扫描,若是操作数,则将字符转换成整数进栈;若是运算符,则连续出栈两次,第一出栈的元素是第二个操作数,第二次出栈的元素是第一个操作数,根据当前的运算符做相应的运算,并将结果进栈,直到‘#’为止。此时栈中只剩下一个元素,即最后的结果,出栈即刻。
int suffix_value(char a[])//a指向后缀表达式
{int i = 0, x1,x2, result;LinkStack S=NULL;while (a[i]!='#'){switch (a[i]){case '+':PopLinkStack(&S, &x2);PopLinkStack(&S, &x1);PushLinkStack(&S, x1 + x2);break;case '-':PopLinkStack(&S, &x2);PopLinkStack(&S, &x1);PushLinkStack(&S, x1 - x2);break;case '*':PopLinkStack(&S, &x2);PopLinkStack(&S, &x1);PushLinkStack(&S, x1 * x2);break;case '/':PopLinkStack(&S, &x2);PopLinkStack(&S, &x1);PushLinkStack(&S, x1 / x2);break;default:PushLinkStack(&S, a[i] - '0');}//end_switchi++;//访问下一个}PopLinkStack(&S, &result);return result;
}//suffix_value
2.3.将算术表达式转换为后缀表达式
为了方便将算术表达式转换成后缀表达式,不妨在算术表达式的末尾增加一个字符‘#’,在算术运算符中增加一个‘#’运算符。
用一个字符栈来存放运算符。先用‘#’初始化字符栈,再对表达式字符串中的每一个字符从左到右依次做一下处理。
(1)如果当前字符是操作数,则将其存放到后缀表达式中数组中。
(2)如果当前字符是运算符,则考虑它是否进栈。
设当前运算符为op,则
(1)当op == ‘(’ 时,op直接进栈。
(2)当op == ‘)’ 时,栈顶运算符依次出栈,并依次将其按顺序存放到后缀表达式数组,直到遇到’)‘为止。注意:’('只是出栈,不存放到后缀表达式数组。
(3)当op的优先级高于栈顶运算符的优先级时,op进栈;否则,栈顶的运算符依次出栈,存放到后缀表达式数组中,直到栈顶的运算符的优先级低于op,op进栈。
(4)当op == ‘#’ ,栈顶运算符依次出栈,存放到后缀表达式数组,直到栈顶运算符为‘#’,算法结束。
设运算符的优先级为#,(,+或-,*或/,从左到右由低到高。
判断优先级的算法
int prior(char a)
{if (a == '*' || a == '/'){return 4;}else if (a == '-' || a == '+'){return 3;}else if (a == '('){return 2;}else if(a=='#'){return 1;}return 0;
}
将算术表达式转换成后缀表达式的算法如下:
【算法】
void Transformation(char a[], char suff[])
{//a指向算术表达式,以'#'结束,栈用于存放运算符//将a指向的算术表达式转换成由suff指向的后缀表达式int i = 0;int k = 0;int n;char ch;LinkStack s;s = NULL;PushLinkStack(&s, '#');n = strlen(a);//在表达式的末尾添加一个#a[n] ='#';a[n + 1] = '\0';while (a[i] != '\0'){if (a[i] >= '0' && a[i] <= '9'){//是操作数,直接存入后缀表达式suff[k++] = a[i];}//是运算符else{switch (a[i]){case '(':PushLinkStack(&s, a[i]);//进栈break;case ')'://将左圆括号之上的运算符依次出栈并发送到后缀表达式,左圆括号只是出栈PopLinkStack(&s, &ch);while (ch != '('){suff[k++] = ch;PopLinkStack(&s, &ch);}break;/*比较表达式当前的运算符a[i]和栈顶运算符的ch的优先级,如果a[i]高于ch,a[i]进栈;反之,栈内高于a[i]的运算符依次出栈并发往后缀表达式直到栈顶运算符优先级低,在将a[i]进栈*/default:GetTopStack(s, &ch);while (prior(ch) >= prior(a[i])){suff[k++] = ch;GetTopStack(s, &ch);}if (a[i] != '#'){PushLinkStack(&s, a[i]);}}//end_switch}//end_elsei++;}//end_whilesuff[k] = '\0';//保证suff存放的是字符串
}//Transformation
以上算法仅适用用于操作数是个位数。要计算任意实数,需要解决如下问题。
(1)后缀表达式中的操作数与操作数之间如何隔开。
(2)操作数栈的类型是什么?
(3)如何将一个数字串转换为一个实数?
(4)操作数为负数的时,如何处理?
例如,算术表达式为-3+(-15.7+9)* 4.25 + 7/8.2
(1)先处理负数的情况。
原则:第一个字符为‘-’时,前面加0;‘("之后是’-‘,在’('之后加0。
(2)在操作数与操作数之间加空格。
2.4.算术表达式直接求值
算法的主要步骤如下。
(1)创建两个栈,一个是运算符栈(初始化时,将’#'进栈),另一个是操作数中间结果栈。
(2)对算术表达式从左向右的依次扫描。
①如果算数表达式的当前字符是操作数,则将算术表达式当前的字符转换成整数进操作数栈。
②如果算术表达式的当前字符是运算符,则将运算符栈的栈顶运算符进行比较。
- 如果算术表达式的当前运算符优先级低于栈顶的运算符优先级,则栈顶的运算符出栈,从操作数栈连续弹出两个操作数,先出的操作数第二运算对象,后出的操作数是第一个运算对象,对两个操作数做出栈运算符对应的操作,并将计算结果结果进操作数栈,直至栈顶运算符的优先级低于算术表达式的当前运算符的优先级为止,再将算术表达式的当前运算符进算符栈。
- 如果算术表达式的当前运算符优先级高于栈顶的运算符优先级,则将算术表达式的当前运算符进运算符栈。
(3)如果算术表达式的当前运算符是’#‘,则依次弹出运算符栈的运算符,同时从操作数连续弹出两个操作数做相应的操作,并将计算结果进操作数栈,直至栈顶的运算符为’#',算法结束。
3.栈与递归
3.1.递归算法
递归是计算机数值计算中的一个中要算法,它可以将复杂的运算转化为若干重复的简单运算,充分发挥计算机重复处理的特点。把递归算法推广为调用自身的方法称为递归算法。
递归实质是将一个不好或不能直接求解的“大问题”转化为一个或几个“小问题”来解决,这些小问题可以继续分解成更小的问题,直至小问题可以直接求解。下面分别介绍这两种常用的递归设计。
- 递归设计方法一
通过将问题简化为自身更小的形式来得到问题解的方法称为递归算法,递归算法必须包含一个或多个基本公式。
递归算法的应用条件如下:
(1)可以将要解决的问题转化为另一个新问题,而解决这个新问题的方法与原问题的解决方法相同,并且被处理的对象的某些参数是有规律地递增或递减的。其中转化的过程成为一般公式。
(2)必须有终止递归的条件(基本公式),即递归出口。
编写递归算法必须做到以下几点。
①确定限制条件或问题的规模。
②确定基本公式。
③确定一般公式。 - 递归设计方法二
对于一个输入规模为n的函数或问题,用某种方法把输入分割成k个子集,从而产生k个字问题,分别求解这个k个子问题,得出k个问题的字解。有些子问题可以直接得到解决,有些子问题的解决方法与原问题相同,再用某种方法把它们组合成原来问题的解。
递归文章详细解析+题目介绍
3.2.栈与函数调用
(1)函数的嵌套调用
main()->fun()->gun()
问题1:每个函数调用完成后,执行流程转向何处?
问题2:执行流程转向被调函数后,继续向下执行,被调用的参数的内部变量在哪里保存?
(2)函数调用的管理
用高级语言编写的程序中,主调函数与被调函数之间的信息交换通过栈来进行。当一个函数在运行期间调用另一个函数时,在运行该别调函数之前,需先完成三件事。
- 将所有的实参和返回地址等信息传递给被调函数保护。
- 为被调函数的局部变量分配存储区。
- 将控制转移到被调函数的入口。
从被调函数返回调用函数之前,也应该完成三件事。
- 保存被调函数的计算结果。
- 释放被调函数中形参和局部变量的存储区。
- 依照被调函数保存的返回地址将控制转移到主调函数。
多个函数嵌套调用的规则是:先调用函数后返回,后调用函数先返回。系统对调函数的内存管理实行的“栈式管理”。
3.3.递归工作与递归函数
递归函数是指定义在一个函数的过程中直接或间接地调用该函数本身。
递归工作栈的记录是一个结构体类型的数据,包括:
(1)上一层函数调用的放回地址。
(2)局部变量(包括参数)值。
系统工作栈的栈顶工作记录对应的是当前正在调用的函数。每调一次函数,将函数的返回地址和局部变量(包括参数)表形成一个递归工作记录压入系统工作栈。每调用完一次函数,将系统工作栈的栈顶工作记录弹出,直至系统工作栈为空。栈空表明递归函数调用结束。
递归算法的特点如下。
- 优点:程序易于设计,程序结构简单精炼。
- 缺点:递归算法较难理解,可读性差;程序运行速度慢,占用相当多的系统资源空间。
3.4.递归到非递归的转换
递归的缺点很明显,所以能用循环就不要用递归。
(1)直接转换法。
如果递归算法是直接求值,不需要回溯,则只需要变量保存中间的结果,将递归结果改为循环结构。
(2)间接转换法
按照递归的执行规律进行转换,将递归调用语句改为进栈操作,将每次递归返回调用后的后续执行语句改为出栈操作。
//将任意一个整数按数字字符显示的递归函数如下void change(int x)
{int n;if (n = x / 10){change(n);//进栈}putchar(x % 10 + 48);//出栈
}
//转换成非递归
void change(int x)
{int n;STACK s;s = NULL;if (x == 0){putchar(x + 48);return;}while (x){//进栈push(s, x % 10);x /= 10;}while (!empty(s)){pop(s, n);//出栈putchar(n + 48);}putchar('\n');
}
相关文章:
)
数据结构——第三章 栈与队列(2)
栈的运用1.括号匹配2.表达式求值2.1.算术表示式的形式2.2.后缀表达式求值2.3.将算术表达式转换为后缀表达式2.4.算术表达式直接求值3.栈与递归3.1.递归算法3.2.栈与函数调用3.3.递归工作与递归函数3.4.递归到非递归的转换1.括号匹配 void matching(char str[]) {//创建空栈Lin…...
【Linux学习】基础IO——理解缓冲区 | 理解文件系统
🐱作者:一只大喵咪1201 🐱专栏:《Linux学习》 🔥格言:你只管努力,剩下的交给时间! 基础IO☕理解缓冲区🧃缓冲区的共识🧃缓冲区的位置🧃缓冲区的刷…...

RHCSA-重置root密码(3.3)
方法1:rd.break (1)首先重启系统,在此页面按e键,在屏幕上显示内核启动参数 (2)知道linux这行,末尾空格后输入rd.break,然后按ctrlx (3)查看&#…...
无公网IP快解析实现U+随时随地访问
现阶段商品从生产到消费者手中要经过多个环节,为实现对每一个环节进行管理,越来越多的企业选择通过信息化手段来实现。供应链管理系统配合供应链中各实体的业务需求,使操作流程和信息系统紧密配合,做到各环节无缝链接,…...

UVa 307 Sticks 木棍拼接 ID 迭代加深搜
题目链接:Sticks 题目描述: 小明一开始有一些长度相等的木棍,小明现在将木棍砍成了一些长度为整数的木棍,他现在忘记了最开始木棍的长度,你需要找到最短的可能木棍长度,例如给定5,2,1,5,2,1,5,2,15,2,1,5,2…...
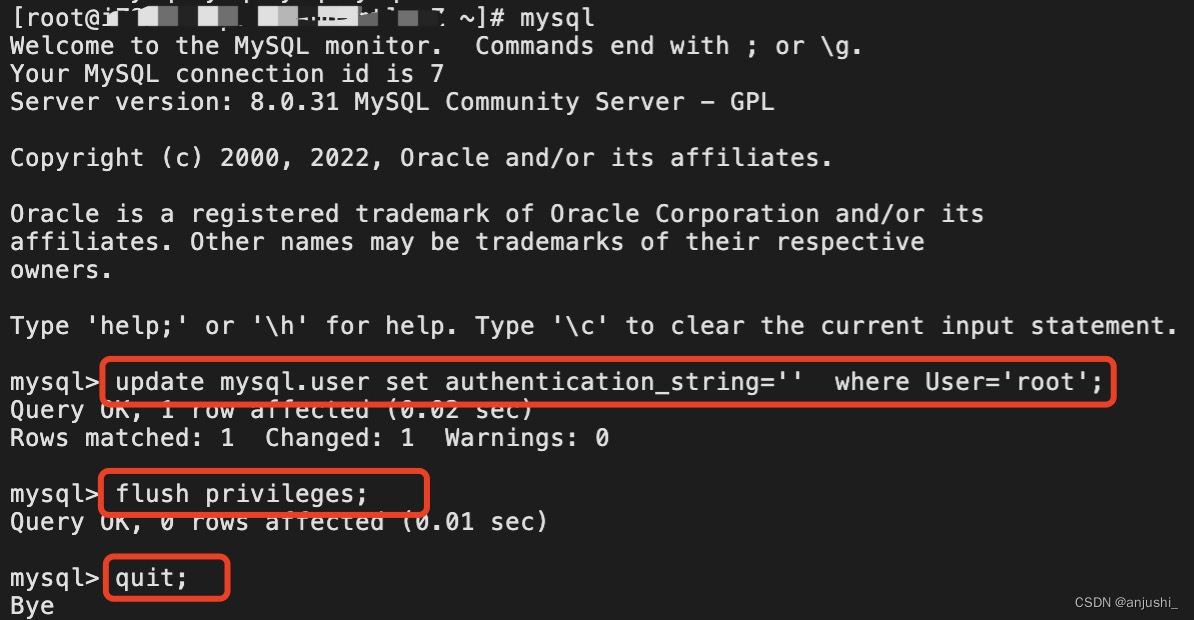
阿里云(CentOS)中MySQL8忘记密码的解决方法
阿里云(CentOS)中MySQL8忘记密码的解决方法 方法 在 skip-grant-tables 模式下启动 MySQL,该模式下启动 MySQL 时不启动授权表功能,可以直接免密码登录 实现 编辑 /etc/my.cnf 文件 vim /etc/my.cnf在 [mysqld] 区域末尾添加配置,设置免密…...
三、Spring的入门程序
第一个Spring程序 创建新的空工程spring6 设置JDK版本17,编译器版本17 设置IDEA的Maven:关联自己的maven 在空的工程spring6中创建第一个maven模块:spring6-001-first 在pom.xml添加spring context依赖和junit依赖, <?x…...
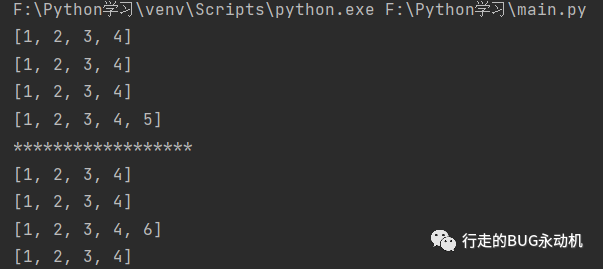
摘录一下Python列表和元组的学习笔记
1 基础概念 列表一个值,列表值指的是列表本身,而不是列表中的内容 列表用[]表示 列表中的内容称为 表项 len()函数可以显示列表中表项的个数,比如下面这个例子 spam [cat, bat, dog, rat]print(len(spam))列表的范围选取中,比…...

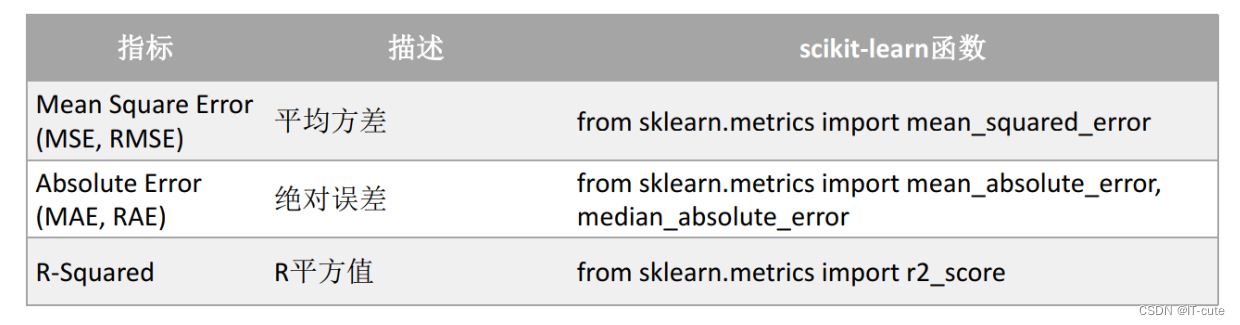
【量化金融】收益率、对数收益率、年华收益、波动率、夏普比率、索提诺比率、阿尔法和贝塔、最大回撤
【量化金融】收益率、对数收益率、年华收益、波动率、夏普比率、索提诺比率、阿尔法和贝塔、最大回撤 1 收益率 在学术界,建模一般不直接使用资产价格,而是使用资产收益率(Returns)。因为收益率比价格具有更好的统计特性,更便于建模。下经典…...
1_机器学习概述—全流程
文章目录1 机器学习定义2 机器学习常见应用框架(重点)3 机器学习分类3.1 监督学习(Supervised learning)3.2 无监督学习(Unsupervised learning)3.3 半监督学习(Semi-Supervised Learning&#…...

VUE中给对象添加新属性时,界面不刷新怎么办
一、直接添加属性的问题 举例: 定义一个p标签,通过v-for指令进行遍历 然后给botton标签绑定点击事件,我们预期点击按钮时,数据新增一个属性,界面也 新增一行。 <p v-for"(value,key) in item" :key&qu…...

视频号频出10w+,近期爆红的账号有哪些?
回顾2月,视频号持续放出大动作,不仅进行了16小时不间断的NBA全明星直播,还邀请国际奥委会入驻,分享奥运的最新资讯。视频号成为越来越多官方机构宣传推广的有效渠道。官方积极入驻,内容创作生态也在同步繁荣发展&#…...
企业寄件现代化管理教程
现代化企业为了跟上时代发展的步伐,在不断完善着管理制度,其中公司寄件管理,也是重要的一个模块。为了提高公司快递的寄件效率,以及节约寄件成本,实现快递寄件的规范化,越来越多的现代化企业,开…...

django 在网页显示后台进度
1、定义函数打开网页 def PeformanceIndex(request): citys{‘wuhu’: ‘芜湖’, ‘xuancheng’: ‘宣城’, ‘tongling’: ‘铜陵’, ‘suzhou’: ‘宿州’, ‘maanshan’: ‘马鞍山’, ‘liuan’: ‘六安’, ‘huainan’: ‘淮南’, ‘huabei’: ‘淮北’, ‘hefei’: ‘合肥…...
)
机器学习库(Numpy, Scikit-learn)
Numpy 创建数组 import numpy as npa np.array([1,2,3]) b np.array([(1.5,2,3), (4,5,6)], dtype float) c np.array([[(1.5,2,3), (4,5,6)], [(3,2,1), (4,5,6)]],dtype float)创建占位符 z1np.zeros((3,4)) z2np.ones((2,3,4),dtypenp.int16) z3d np.arange(10,25,5)…...

Linux操作系统学习(进程替换)
文章目录进程替换进程替换是什么?替换的方法进程替换简易shell模拟进程替换 进程替换是什么? 如下图所示: 进程替换就是,把进程B的代码和数据,替换正在执行的进程A的代码和数据在内存中的位置(若代码…...

【C++从入门到放弃】类和对象(中)———类的六大默认成员函数
🧑💻作者: 情话0.0 📝专栏:《C从入门到放弃》 👦个人简介:一名双非编程菜鸟,在这里分享自己的编程学习笔记,欢迎大家的指正与点赞,谢谢! 类和对…...

白盒测试重点复习内容
白盒测试白盒测试之逻辑覆盖法逻辑覆盖用例设计方法1.语句覆盖2.判定覆盖(分支覆盖)3.条件覆盖4.判定条件覆盖5.条件组合覆盖6.路径覆盖白盒测试之基本路径测试法基本路径测试方法的步骤1.根据程序流程图画控制流图2.计算圈复杂度3.导出测试用例4.准备测试用例5.例题白盒测试总…...

【13】linux命令每日分享——groupadd建立组
大家好,这里是sdust-vrlab,Linux是一种免费使用和自由传播的类UNIX操作系统,Linux的基本思想有两点:一切都是文件;每个文件都有确定的用途;linux涉及到IT行业的方方面面,在我们日常的学习中&…...
《第一行代码》 第十章:服务
一,在子线程中更新UI 1,新建项目,修改布局代码 <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"&g…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
