【Golang】IEEE754标准二进制字符串转为浮点类型
IEEE754介绍
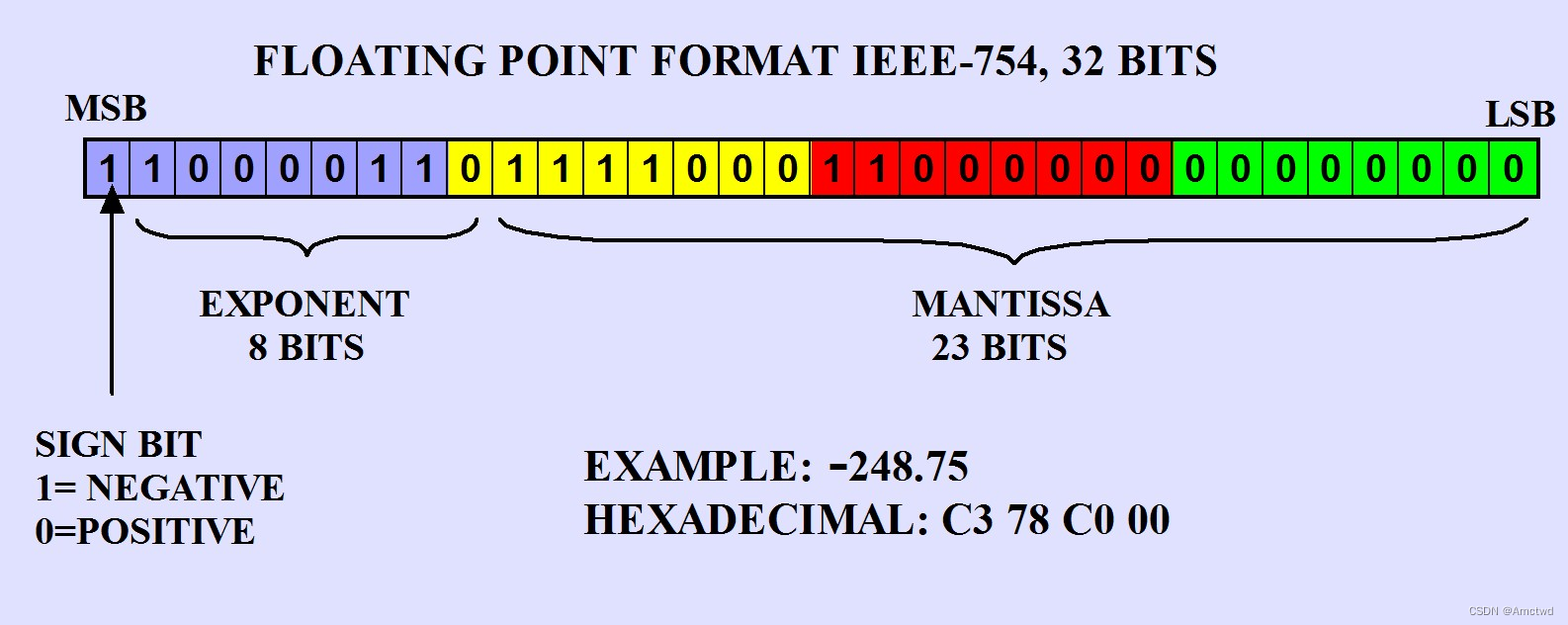
IEEE 754是一种标准,用于表示和执行浮点数运算的方法。在这个标准中,单精度浮点数使用32位二进制表示,分为三个部分:符号位、指数位和尾数位。
符号位(s)用一个位来表示数的正负,0表示正数,1表示负数。
指数位(e)用8位表示指数。对于单精度浮点数,指数位是以偏移量的形式表示的。也就是说,实际的指数值是指数位的无符号值减去一个偏移量(127)。
尾数位(m)用23位表示数的尾数部分。尾数是一个二进制小数,被规范化为一个小于1的数。
表达式:
V = ( − 1 ) s × ( 1. M ) × 2 ( E − 127 ) V = (-1)^s \times(1.M)\times 2^{(E-127)} V=(−1)s×(1.M)×2(E−127) (单精度)
V = ( − 1 ) s × ( 1. M ) × 2 ( E − 1023 ) V = (-1)^s \times(1.M)\times 2^{(E-1023)} V=(−1)s×(1.M)×2(E−1023)(双精度)
| IEEE 754 半精度浮点数 | 16 位 | 符号 1 位,指数 5 位,尾数 10 位 |
| IEEE 754 单精度浮点数 | 32 位 | 符号 1 位,指数 8 位,尾数 23 位 |
| IEEE 754 双精度浮点数 | 64 位 | 符号 1 位,指数 11 位,尾数 52 位 |
代码实现计算
我们首先定义了一个函数binaryIEEE754StringToFloat,它接收一个32位的二进制字符串作为输入,并返回一个浮点数。该函数首先确定输入字符串的长度,并在必要时进行填充,使其达到32位。
接下来,我们解析符号位、指数位和尾数位。符号位确定数的正负,指数位确定数的范围,尾数位确定数的精度。通过这些步骤,我们能够将二进制字符串转换为浮点数。
最后,我们在main函数中提供了一个示例二进制字符串,并调用binaryIEEE754StringToFloat函数进行转换。输出结果是一个浮点数,它就是我们所求的结果。
package main
import ("fmt""math""strconv""strings"
)
func binaryIEEE754StringToFloat(binaryStr string) float32 {n := 32 - len(binaryStr)// 补充为32位if n >= 0 && n < 32 {binaryStr = strings.Repeat("0", n) + binaryStr} else {fmt.Println("二进制字符串的长度不合法")return 0}// 解析符号位sign := 1.0if binaryStr[0] == '1' {sign = -1.0}// 解析指数位
(exponent, _ := strconv.ParseInt(binaryStr[1:9], 2, 64))
(exponent -= 127)// 解析尾数位
(mantissa := float32(0))for i := 9; i < len(binaryStr); i++ {if binaryStr[i] == '1' {(mantissa += 1 / float32(math.Pow(2, float64(i-8))))}}// 计算浮点数值
(result := float32(sign) * (1 + mantissa) * float32(math.Pow(2, float64(exponent))))return result
}
func main() {
(binaryStr := "10111111100111101110101110000000") // 示例二进制字符串
(floatVal := binaryIEEE754StringToFloat(binaryStr))fmt.Printf("转换后的浮点数为: %f\n", floatVal)
}
补充(Double类型转换):
func BinaryDoubleStringToFloat(binaryStr string) float64 {// 补充为64位n := 64 - len(binaryStr)if n >= 0 && n < 64 {binaryStr = strings.Repeat("0", n) + binaryStr} else {fmt.Println("二进制字符串的长度不合法")return 0}// 解析符号位sign := 1.0if binaryStr[0] == '1' {sign = -1.0}// 解析指数位exponent, _ := strconv.ParseInt(binaryStr[1:12], 2, 64)exponent -= 1023 // 双精度指数位的偏移量// 解析尾数位mantissa := float64(0)for i := 12; i < len(binaryStr); i++ {if binaryStr[i] == '1' {mantissa += 1 / float64(math.Pow(2, float64(i-11)))}}// 计算浮点数值result := sign * (1 + mantissa) * math.Pow(2, float64(exponent))return result
}
相关文章:

【Golang】IEEE754标准二进制字符串转为浮点类型
IEEE754介绍 IEEE 754是一种标准,用于表示和执行浮点数运算的方法。在这个标准中,单精度浮点数使用32位二进制表示,分为三个部分:符号位、指数位和尾数位。 符号位(s)用一个位来表示数的正负,0表示正数,1表…...
【开源项目】轻量元数据管理解决方案——Marquez
大家好,我是独孤风。 又到了本周的开源项目推荐。最近推荐的元数据管理项目很多,但是很多元数据管理平台的功能复杂难用。 那么有没有轻量一点的元数据管理项目呢? 今天为大家推荐的开源项目,就是一个轻量级的元数据管理工具。虽然…...

dirty file page
转自:https://www.cnblogs.com/zhiminyu/p/17330763.html 0.前言 Linux 内核Page Cache 和Buffer Cache 关系及演化历史 一文中讲过Linux 2.4之后将Page Cache和Buffer Cache 进行了融合,在buffer_head 中添加了b_page,很容易就能找到缓存的…...

HTAP(Hybrid Transactional/Analytical Processing)系统之统一存储的实时之道
文章目录 HTAP与时俱进LASER中的存储关键知识LSM(Log-Structured Merge Tree)SkipList(跳表)CDC(Changed Data Capture)SST(Sorted Sequence Table) 特性列组(Column Gro…...

【linux】tcpdump 使用
tcpdump 是一个强大的网络分析工具,可以在 UNIX 和类 UNIX 系统上使用,用于捕获和分析网络流量。它允许用户截取和显示发送或接收过网络的 TCP/IP 和其他数据包。 一、安装 tcpdump 通常是默认安装在大多数 Linux 发行版中的。如果未安装,可…...
数字图像处理常用算法的原理和代码实现详解
本专栏详细地分析了常用图像处理算法的数学原理、实现步骤。配有matlab或C实现代码,并对代码进行了详细的注释。最后,对算法的效果进行了测试。相信通过这个专栏,你可以对这些算法的原理及实现有深入的理解! 如有疑问…...

Pandas实战100例 | 案例 26: 检测异常值
案例 26: 检测异常值 知识点讲解 在数据分析中,检测和处理异常值(或离群值)是一个重要的步骤。异常值可能会影响数据的整体分析。一种常用的方法是使用四分位数和四分位数间距(IQR)来识别异常值。 四分位数和 IQR: …...
C语言学习NO.11-字符函数strlen,strlen函数的使用,与三种strlen函数的模拟实现
(一)strlen函数的使用 strlen函数的演示 #include <stdio.h> #include <string.h>int main() {char arr1[] "abcdef";char arr2[] "good";printf("arr1 %d,arr2 %d",strlen(arr1),strlen(arr2));return …...

Vue3+ts获取props的值并且定义props值的类型的方法。
1.引入withDefaults模块,给defineProps绑定默认值。 import { withDefaults } from vue2.定义Props传输值的类型。 interface Props {// 类型type: string;name: string;id: number; }3.给props的值设置默认值。 const props withDefaults(defineProps<Prop…...

EasyExcel 不使用科学计数发并以千分位展示
EasyExcel 不使用科学计数发并以千分位展示 不使用科学计数法 不使用科学计数法 BigDecimalStringConverter 将 BigDecimal 类型的数值转换为字符串类型,并将其导出到 Excel 文件中。在 convertToExcelData 方法中,我们将 BigDecimal 转换为字符串&…...

【Python机器学习】SVM——调参
下面是支持向量机一个二维二分类数据集的训练结果: import mglearn import matplotlib.pyplot as plt from sklearn.svm import SVCplt.rcParams[font.sans-serif] [SimHei] plt.rcParams[axes.unicode_minus] False X,ymglearn.tools.make_handcrafted_dataset()…...
网络传输(TCP)
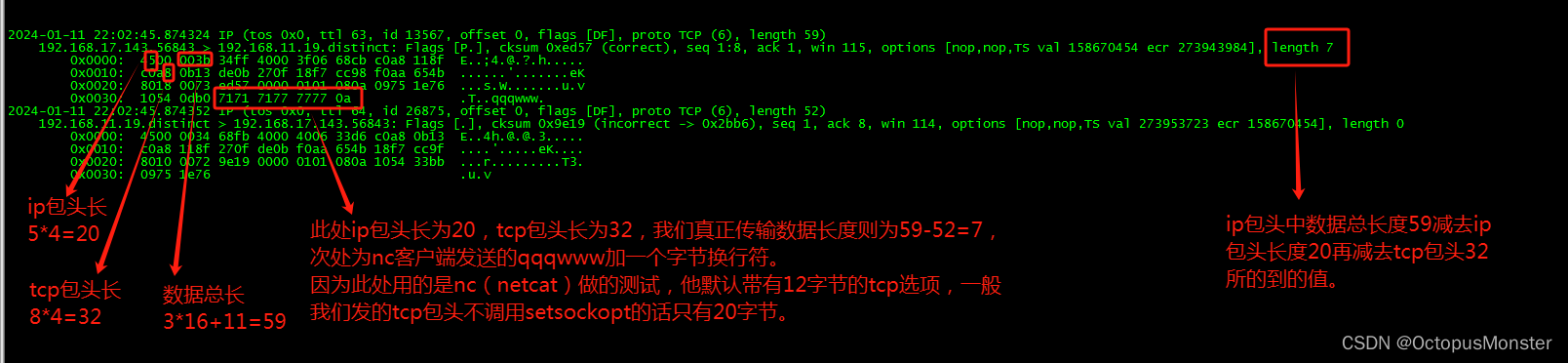
前言 我们tcpdump抓包时会看到除报文数据外,前面还有一段其他的数据,这段数据分为两部分,ip包头(一般20字节)和tcp包头(一般20字节),一般这两个头长度和为40,我们直接跳…...

MFC模拟消息发送,自定义以及系统消息
在MFC框架下,有很多系统已经定义好的消息,例如ON_WM_LBUTTONDOWN()、ON_WM_MBUTTONDOWN()等等。我们在使用的时候只需要声明并调用就可以了,最简单的用法。 提升了一点难度的用法就是自己设置自定义消息,再提升一点难度的就是如何…...

并发,并行,线程与UI操作
并行和并发是计算机领域中两个相关但不同的概念。 并行(Parallel)指的是同时执行多个任务或操作,它依赖于具有多个处理单元的系统。在并行计算中,任务被分成多个子任务,并且这些子任务可以同时在不同的处理单元上执行…...

react 6种方式编写样式
在React中,编写样式主要有以下几种方式: 1. 内联样式: 直接在React组件中使用style属性来定义样式。这种方式比较适合定义动态的样式,因为它允许你将JavaScript表达式作为样式的值。 2. 外部样式表 :通过创建外部的…...
计算机找不到msvcr100.dll的多种解决方法分享,轻松解决dll问题
msvcr100.dll作为系统运行过程中不可或缺的一部分,它的主要功能在于提供必要的运行时支持,确保相关应用程序能够顺利完成编译和执行。因此,当操作系统或应用程序在运行阶段搜索不到该文件时,自然会导致各类依赖于它的代码无法正常…...

系分笔记数据库反规范化、SQL语句和大数据
文章目录 1、概要2、反规范化3、大数据4、SQL语句5、总结 1、概要 数据库设计是考试重点,常考和必考内容,本篇主要记录了知识点:反规范化、SQL语句及大数据。 2、反规范化 数据库遵循范式的设计,使得多表查询和连接表查询较多的时…...

php实现支付宝商户转账
目录 一:背景介绍 一:准备工作 三:代码实现 一:背景介绍 最近工作中,要用到支付宝的商家转账功能,用php代码实现,网上找的内容,有些是老版本的实现,有些是调用sdk&am…...
)
并发编程(十一)
性能测试的常用命令 1、Netstat是在内核中访问网络连接状态及其相关信息的程序,它能够显示协议统计和当前TCP/IP的网络连接。 Netstat命令的常用格式如下: netstat -a:显示所有网络连接和侦听端口。 netstat -b:显示在创建网络…...

vue3 指令详解
系列文章目录 TypeScript 从入门到进阶专栏 文章目录 系列文章目录前言一、v-model (双向绑定功能)二、v-bind(用于将一个或多个属性绑定到元素的属性或组件的 prop)三、v-if、v-else、v-else-if(用于根据条件选择性地渲染元素)四、v-show(根…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
