LeetCode 面试题 05.02. Binary Number to String LCCI【字符串,数学】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
Given a real number between 0 and 1 (e.g., 0.72) that is passed in as a double, print the binary representation. If the number cannot be represented accurately in binary with at most 32 characters, print “ERROR”.
Example1:
Input: 0.625
Output: "0.101"
Example2:
Input: 0.1
Output: "ERROR"
Note: 0.1 cannot be represented accurately in binary.
Note:
- This two charaters “0.” should be counted into 32 characters.
- The number of decimal places for
numis at most 6 digits
题意:给出一个介于0到1之间的实数,作为一个 double 被传入函数中,题目要求打印该实数的二进制表示。如果不能用「最多32个字符的二进制字符串」表示该实数,则打印"ERROR"。比如说,0.625100.625_{10}0.62510 的二进制字符串表示是 0.10120.101_{2}0.1012 ,其中 "0." 这两个字符也要算入32个字符中。
解法一 十进制小数转为二进制数
介于0和1之间的实数的十进制整数部分是 000 ,小数部分大于 000 ,因此其二进制表示的整数部分是 000 ,需要将小数部分转换成二进制表示。
示例1中十进制数 0.6250.6250.625 可以写成 121+123\dfrac{1}{2^1} + \dfrac{1}{2^3}211+231 ,因此对应的二进制数是 0.101(2)0.101_{(2)}0.101(2) ,二进制数中的左边的 111 为小数点后第一位,表示 12\dfrac{1}{2}21 ,右边的 111 为小数点后第三位,表示 123\dfrac{1}{2^3}231 。
如果将十进制数 0.6250.6250.625 乘以 222 ,则得到 1.251.251.25 ,可以写成 1+1221 + \dfrac{1}{2^2}1+221 ,因此对应的二进制数是 1.01(2)1.01_{(2)}1.01(2) 。二进制数 0.101(2)0.101_{(2)}0.101(2) 的两倍是 1.01(2)1.01_{(2)}1.01(2) ,在二进制表示中将一个数乘以 222 的效果是将小数点向右移动一位。
综上所述,将实数的十进制表示转换成二进制表示的方法是:每次将实数乘以 222 ,将此时的整数部分添加到二进制表示的末尾,然后将整数部分置为 000 ,重复上述操作,直到小数部分变成 000 、或者小数部分出现循环时结束操作。当小数部分变成 000 时,得到二进制表示下的有限小数;当小数部分出现循环时,得到二进制表示下的无限循环小数。
由于这道题要求二进制表示的长度最多为 323232 位,否则返回 ERROR ,因此不需要判断给定实数的二进制表示是有限小数还是无限循环小数,而是在小数部分变成 000 或二进制表示的长度超过 323232 位时结束操作。当操作结束时,如果二进制表示的长度不超过 323232 位则返回二进制表示,否则返回 ERROR 。
class Solution {
public:string printBin(double num) {string ans = "0.";while (ans.size() <= 32 && num > 1e-10) {int f = num * 2;ans.push_back('0' + f);num = num * 2 - f;}return ans.size() <= 32 ? ans : "ERROR";}
};
复杂度分析
- 时间复杂度:O(C)O(C)O(C) ,其中 CCC 是结果字符串的最大长度,C=32C = 32C=32 。最多计算 323232 位,每一位的计算时间是 O(1)O(1)O(1) 。
- 空间复杂度:O(C)O(C)O(C) ,其中 CCC 是结果字符串的最大长度,C=32C = 32C=32 。存储结果的字符串需要 O(C)O(C)O(C) 的时间。
解法二 数学优化(最优)
numnumnum 如果可以表示为有限位二进制小数,那么可以表示为一个形如 b2k\dfrac{b}{2^k}2kb 的最简分数,这里 bbb 是整数且与 2k2^k2k 互质(有限位可以不断左移,得到整数 bbb ,再除以 2k2^k2k 就等于原数;由于是最简形式,所以互质)。当 num\textit{num}num 在 (0,1)(0,1)(0,1) 内时,k≥1k\ge 1k≥1 ,bbb 与 2k2^k2k 互质、也就与 222 互质;numnumnum 大于1时,bbb 不一定与 222 互质。例如 0.625=58=5230.625=\dfrac{5}{8}=\dfrac{5}{2^3}0.625=85=235 ,由于5=101(2)5=101_{(2)}5=101(2) ,所以 0.625=0.101(2)0.625=0.101_{(2)}0.625=0.101(2) 。
对于一个十进制小数位数最多有 666 位的数 num\textit{num}num ,可以表示为分数 a106\dfrac{a}{10^6}106a 或者 a26⋅56\dfrac{a}{2^6\cdot 5^6}26⋅56a 。这里不要求是最简分数,只规定 aaa 是整数。
如果 num\textit{num}num 可以表示为有限位二进制小数,则有
a26⋅56=b2k\dfrac{a}{2^6\cdot 5^6}= \dfrac{b}{2^k}26⋅56a=2kb
等号两边同时乘上 2k2^k2k ,得
a⋅2k−656\dfrac{a\cdot 2^{k-6}}{5^6}56a⋅2k−6
由于 bbb 与 222 互质,等号左边不能有因子 222 ,所以 k−6≤0k-6\le 0k−6≤0 ,即 k≤6k\le 6k≤6 ,当 aaa 是奇数时取等号。
因此,当 num\textit{num}num 的十进制小数位数最多只有 666 位时,若 num\textit{num}num 能表示为有限位二进制小数,则二进制小数位数同样至多为 666 位。由于 k≤6k\le 6k≤6 ,循环乘以2六次后,如果 num\textit{num}num 仍不为 000 ,则它必定无法精确地用二进制表示(是一个无限循环二进制小数)。
class Solution {
public:string printBin(double num) {string ans = "0.";while (ans.size() <= 8 && num > 1e-10) { // 6位小数,8位字符int f = num * 2;ans.push_back('0' + f);num = num * 2 - f;}return ans.size() <= 8 ? ans : "ERROR";}
};
复杂度分析
- 时间复杂度:O(1)O(1)O(1) 。
- 空间复杂度:O(1)O(1)O(1) 。
思考题
如果转换成 ppp 进制呢?根据上面的证明过程,当 ppp 是多少的时候,num\textit{num}num(十进制小数位数不超过6位)才可能表示为有限位 ppp 进制小数?
b=a×pk106b = \dfrac{a \times p^k}{10^6}b=106a×pk
答:只要 ppp 的因子包含 222 或 555 即 ppp 是 2i×5j2^i\times 5 ^j2i×5j 时,才可以表示有限位 ppp 进制小数。
相关文章:

LeetCode 面试题 05.02. Binary Number to String LCCI【字符串,数学】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

数据结构 “串“ 的补充提升与KMP算法及其优化的具体实现
❤️作者主页:微凉秋意 ✅作者简介:后端领域优质创作者🏆,CSDN内容合伙人🏆,阿里云专家博主🏆 ✨精品专栏:C面向对象 🔥系列专栏:数据结构与课程设计 文章目录…...
消息队列)
如何使用Spring Cloud搭建MQ(Message Queue)消息队列
Spring Cloud是一个开源框架,用于构建基于微服务架构的应用程序。它提供了多种工具和技术,用于实现各种微服务模式,并使它们易于管理和部署。MQ(消息队列)则是一种重要的异步通信机制,用于在不同的应用程序…...
iphone备忘录删除怎么恢复?分享苹果数据找回办法
手机备忘录上写记录,这是不少上班族的小习惯。因为它可以先记录紧急事务,然后再慢慢的解决。也可以把我们一些重要的账号密码存在备忘录里,方便在何时何地直接登入使用。那么如果我们不小心删除了iphone备忘录呢?碰到这种事该怎么办呢?有没…...

【PPT】《我去!还有这种网站?》-知识点目录
《我去!还有这种网站?》 1. Vega AI 输入提示: girl,粉头发2. 物理画线:休闲小游戏 3. Dialogue:影视台词搜索 4. Can you run it:游戏设备要求查询 5. Deviceshots:使用设备边…...

SQL 将查询结果插入到另一张表中
INSERT INTO (1) 如果两张表(导出表和目标表)的字段一致,并且希望插入全部数据,可以用这种方法: INSERT INTO 目标表 SELECT * FROM 来源表 WHERE 条件;例如,要将 test 表插入到 n…...
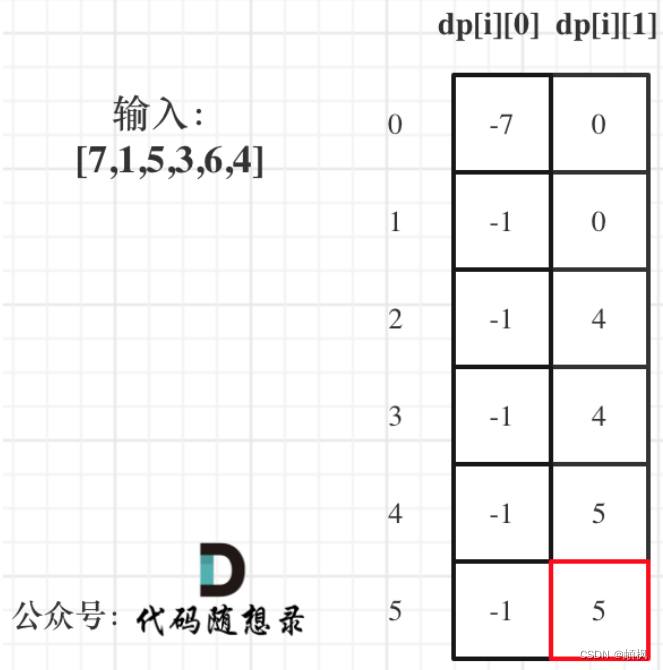
代码随想录算法训练营day48 | 动态规划 121 买卖股票的最佳时机 122 买卖股票的最佳时机II
day48121. 买卖股票的最佳时机1.确定dp数组(dp table)以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例推导dp数组122.买卖股票的最佳时机II121. 买卖股票的最佳时机 题目链接 解题思路: 动规五部曲分析如下:…...

MediaTek 天玑 8000 5G移动平台详细参数
MediaTek 天玑 8000 移动平台 采用先进的 台积电 5nm 工艺,拥有出众的性能和能效,为高端智能手机用户提供出色的高帧率游戏和 5G 移动体验。 天玑 8000 采用了 MediaTek 诸多先进技术,内置 MediaTek Imagiq 780影像引擎、第五代 AI 处理器APU…...

Kafka
这里写目录标题1.Kafka1.1 Kafka概述1.2 kafka安装和配置1.3 入门案例1.4 kafka生产者详解1.4.1 生产者的参数1.Kafka 1.1 Kafka概述 Kafka 是一个分布式流媒体平台,类似于消息队列或企业消息传递系统。 producer:发布消息的对象称之为主题生产者(Ka…...
)
数据结构——第三章 栈与队列(2)
栈的运用1.括号匹配2.表达式求值2.1.算术表示式的形式2.2.后缀表达式求值2.3.将算术表达式转换为后缀表达式2.4.算术表达式直接求值3.栈与递归3.1.递归算法3.2.栈与函数调用3.3.递归工作与递归函数3.4.递归到非递归的转换1.括号匹配 void matching(char str[]) {//创建空栈Lin…...
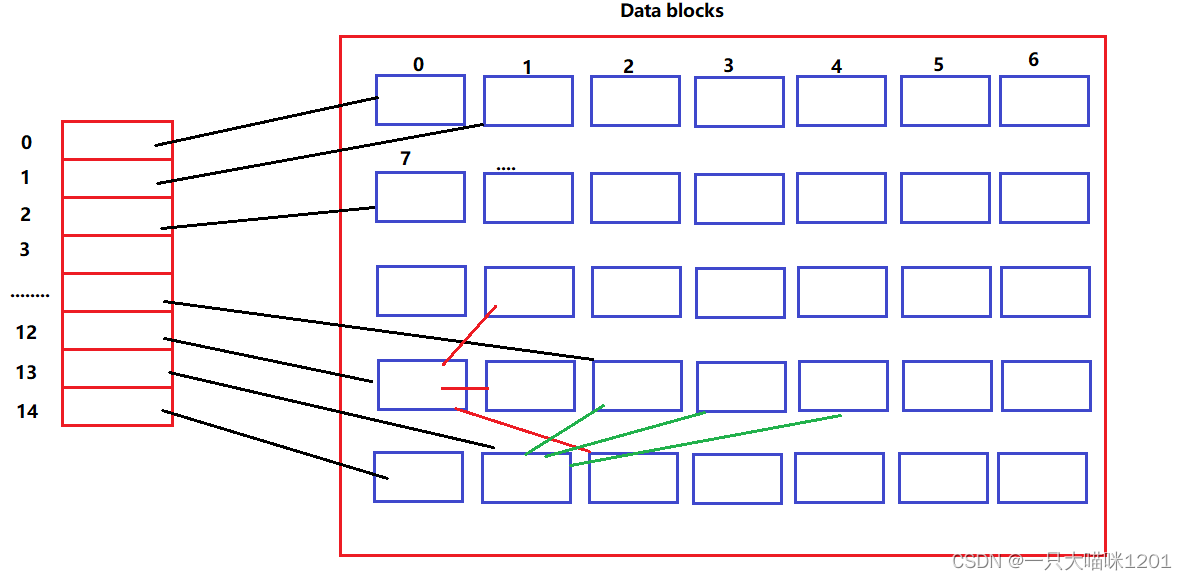
【Linux学习】基础IO——理解缓冲区 | 理解文件系统
🐱作者:一只大喵咪1201 🐱专栏:《Linux学习》 🔥格言:你只管努力,剩下的交给时间! 基础IO☕理解缓冲区🧃缓冲区的共识🧃缓冲区的位置🧃缓冲区的刷…...

RHCSA-重置root密码(3.3)
方法1:rd.break (1)首先重启系统,在此页面按e键,在屏幕上显示内核启动参数 (2)知道linux这行,末尾空格后输入rd.break,然后按ctrlx (3)查看&#…...
无公网IP快解析实现U+随时随地访问
现阶段商品从生产到消费者手中要经过多个环节,为实现对每一个环节进行管理,越来越多的企业选择通过信息化手段来实现。供应链管理系统配合供应链中各实体的业务需求,使操作流程和信息系统紧密配合,做到各环节无缝链接,…...

UVa 307 Sticks 木棍拼接 ID 迭代加深搜
题目链接:Sticks 题目描述: 小明一开始有一些长度相等的木棍,小明现在将木棍砍成了一些长度为整数的木棍,他现在忘记了最开始木棍的长度,你需要找到最短的可能木棍长度,例如给定5,2,1,5,2,1,5,2,15,2,1,5,2…...
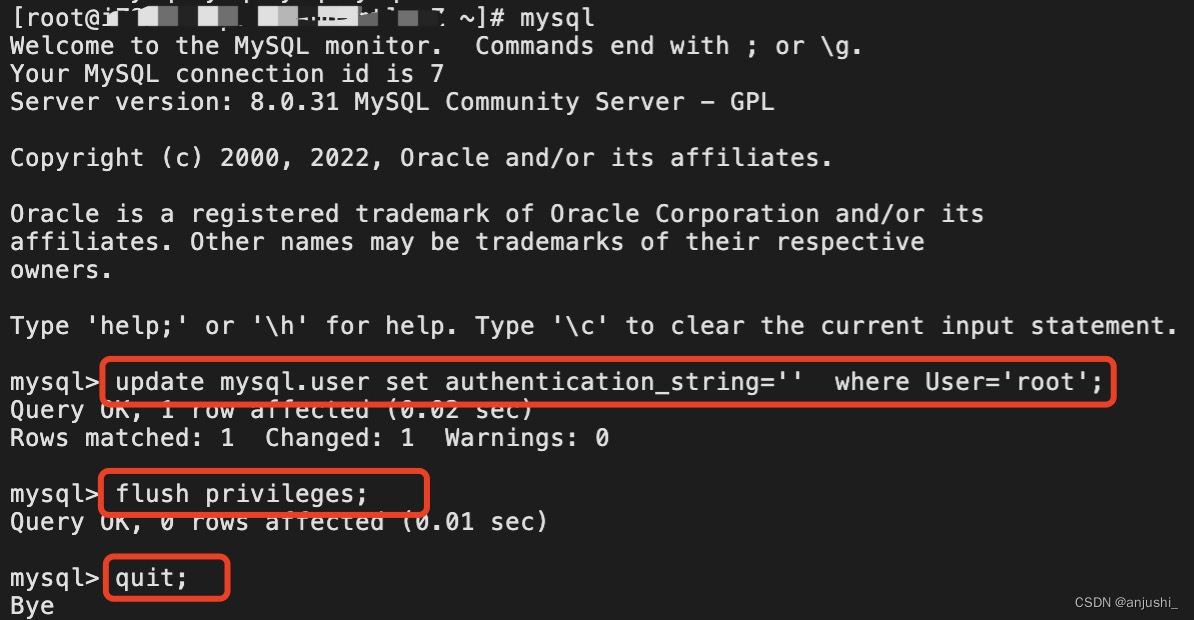
阿里云(CentOS)中MySQL8忘记密码的解决方法
阿里云(CentOS)中MySQL8忘记密码的解决方法 方法 在 skip-grant-tables 模式下启动 MySQL,该模式下启动 MySQL 时不启动授权表功能,可以直接免密码登录 实现 编辑 /etc/my.cnf 文件 vim /etc/my.cnf在 [mysqld] 区域末尾添加配置,设置免密…...
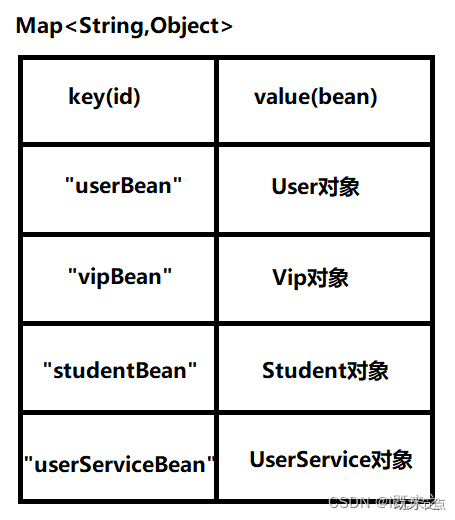
三、Spring的入门程序
第一个Spring程序 创建新的空工程spring6 设置JDK版本17,编译器版本17 设置IDEA的Maven:关联自己的maven 在空的工程spring6中创建第一个maven模块:spring6-001-first 在pom.xml添加spring context依赖和junit依赖, <?x…...
摘录一下Python列表和元组的学习笔记
1 基础概念 列表一个值,列表值指的是列表本身,而不是列表中的内容 列表用[]表示 列表中的内容称为 表项 len()函数可以显示列表中表项的个数,比如下面这个例子 spam [cat, bat, dog, rat]print(len(spam))列表的范围选取中,比…...

【量化金融】收益率、对数收益率、年华收益、波动率、夏普比率、索提诺比率、阿尔法和贝塔、最大回撤
【量化金融】收益率、对数收益率、年华收益、波动率、夏普比率、索提诺比率、阿尔法和贝塔、最大回撤 1 收益率 在学术界,建模一般不直接使用资产价格,而是使用资产收益率(Returns)。因为收益率比价格具有更好的统计特性,更便于建模。下经典…...
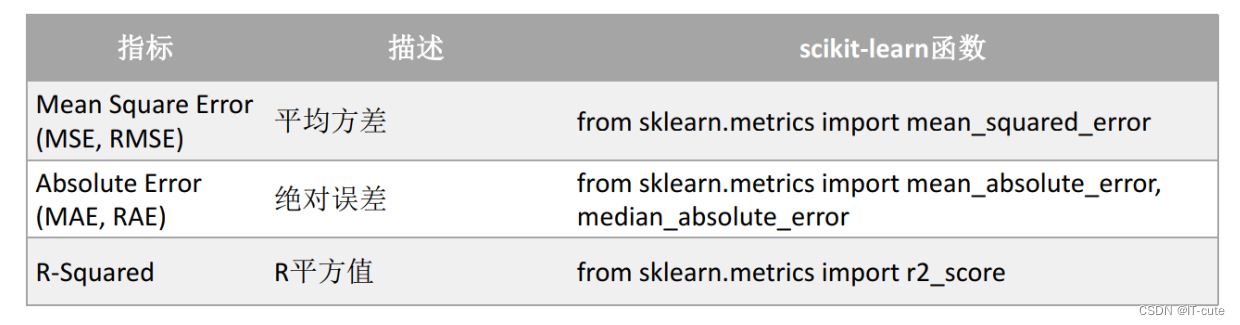
1_机器学习概述—全流程
文章目录1 机器学习定义2 机器学习常见应用框架(重点)3 机器学习分类3.1 监督学习(Supervised learning)3.2 无监督学习(Unsupervised learning)3.3 半监督学习(Semi-Supervised Learning&#…...

VUE中给对象添加新属性时,界面不刷新怎么办
一、直接添加属性的问题 举例: 定义一个p标签,通过v-for指令进行遍历 然后给botton标签绑定点击事件,我们预期点击按钮时,数据新增一个属性,界面也 新增一行。 <p v-for"(value,key) in item" :key&qu…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
