【C++进阶06】红黑树图文详解及C++模拟实现红黑树

一、红黑树的概念及性质
1.1 红黑树的概念
AVL树用平衡因子让树达到高度平衡
红黑树可以认为是AVL树的改良
通过给每个节点标记颜色让树接近平衡
以减少树在插入节点的旋转
在每个结点新增一个存储位表示结点颜色
可以是Red或Black
通过对任何一条从根到叶子的路径上
各个结点着色方式的限制
红黑树确保没有一条路径会比其他路径长出
俩倍,因而是接近平衡的
1.2 红黑树的性质
- 每个结点不是红色就是黑色
- 根节点是黑色的
如果一个节点是红色的
则它的两个孩子结点是黑色的对于每个结点
从该结点到其所有后代叶结点的简单路径上
均包含相同数目的黑色结点- 每个叶子结点都是黑色的
(此处的叶子结点指的是空结点)
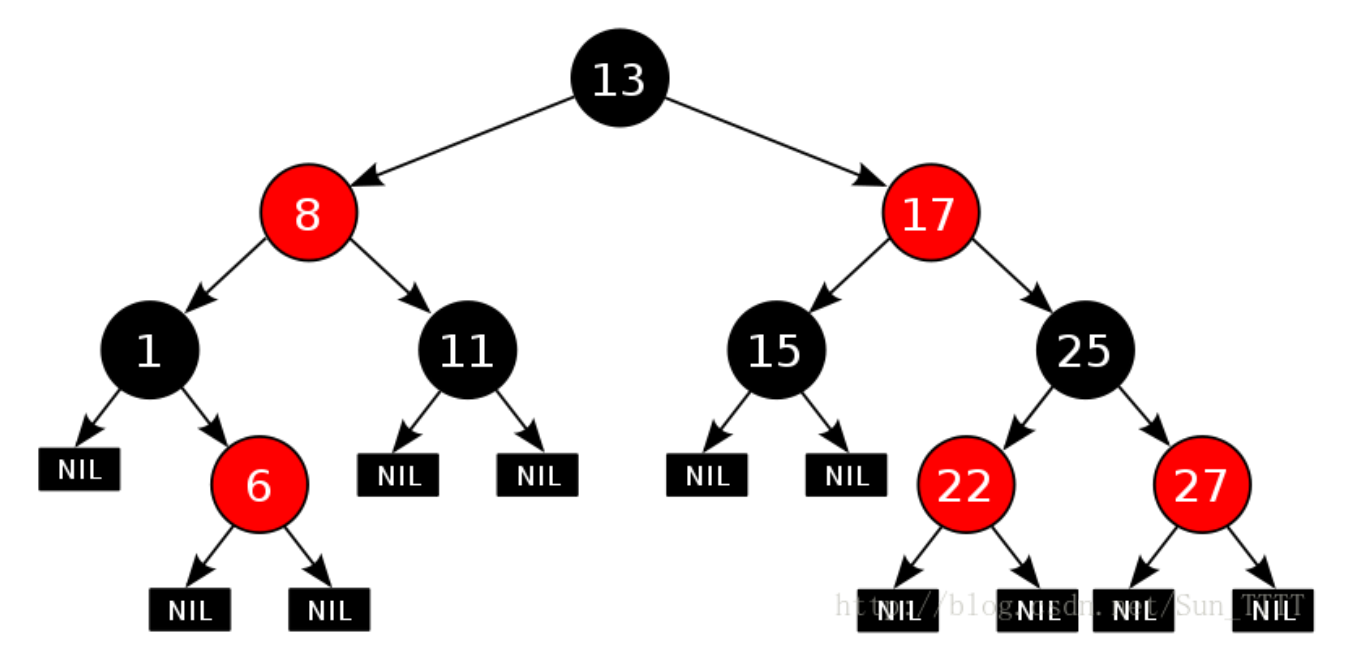
为啥满足上面性质的红黑树就能保证
其最长路径节点个数不会超过最短路径
节点个数的两倍?
由性质3可得出不能出现连续红色节点
由性质4可得出每条路径有相同黑色节点数量
极限情况下
最短路径:全黑
最长路径:一黑一红
由此可得出
最长路径不会超过最短路径的两倍

1.3 为什么更常用红黑树而不是AVL树?
AVL树: 是一颗高度平衡的二叉树
查找效率: O ( l o g N ) O(logN) O(logN)
但是这样的效率是在插入元素时
经常性的旋转换来的
红黑树: 是一颗接近平衡的二叉树
假设全部黑节点有N个
整棵树的节点数量:[N, 2N]之间
最短路径长度: O ( l o g N ) O(logN) O(logN)
最长路径长度: O ( 2 l o g N ) O(2logN) O(2logN)
查找效率: O ( 2 l o g N ) O(2logN) O(2logN)
10亿数据AVL树最多查找30次
红黑树最多也就查找60次
对于cpu的运行速度来说几乎可以忽略不计
但红黑树的规则相对于AVL树没那么严格
在插入元素时,不会经常旋转
所以综合而言红黑树更胜一筹
如图: 对于AVL树必定旋转
红黑树则不用

二、红黑树模拟实现的基本框架
2.1 红黑树节点的定义
跟AVL树一样
只是AVL树采用平衡因子
让树达到平衡
而红黑树对节点进行颜色标记
让树达到平衡
定义一个枚举表示节点颜色
enum colour
{RED,BLACK,
};template <class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent; // 三叉链pair<K, V> _kv;colour _col;RBTreeNode(const pair<K, V>& kv): _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};template <class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:
private:Node* _root = nullptr;
};
2.2 红黑树的插入
还是和AVL树一样
bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first) // 插入节点比当前节点大往右走, 小往左走{parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}// 链接cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}// new的节点的parent还指向空cur->_parent = parent;// 插入黑色节点还是红色节点?return true;}
插入走到这里如果是AVL树
此时需要更新平衡因子
红黑树采用的是标记节点颜色
让树达到平衡
需要考虑的是插入什么颜色的节点?
插入黑色节点
会违反规则4,影响到每条路径插入红色节点
如果插入节点的父节点也是红色节点
则会违反规则3影响当前局部节点
很明显插入红色节点更划算
所有插入的节点都默认是红色
如果违反红黑树的规则,再进行调整
三、对插入节点调整的解析
如果插入节点的父节点为黑
则无需处理
如果为红,则分为三种情况
情况一:
cur为红,p为红,g为黑,u存在且为红
cur为当前节点,p为父节点
g为祖父节点,u为叔叔节点

把p和u变黑,g变红

如果grandfather的parent也为红
把grandfather改为cur
继续按刚才的步骤往后迭代
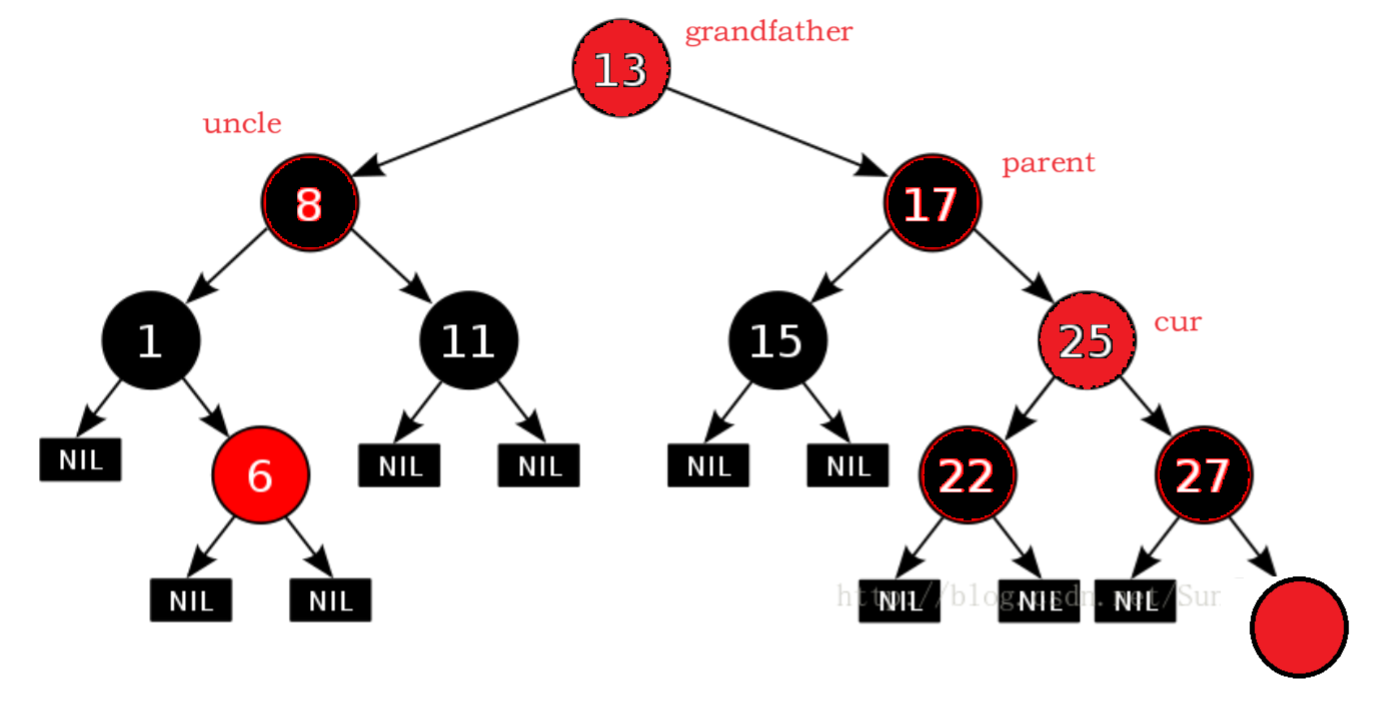
如果grandfather为根节点
把grandfather改为黑色
颜色调整结束

情况二:
cur为红,p为红,g为黑
u不存在或u存在且为黑
此树可能是完整树也可能是子树
u节点不存在

p为g的左孩子,cur为p的左孩子
则进行右单旋转
相反
p为g的右孩子,cur为p的右孩子
则进行左单旋转
p、g变色–p变黑,g变红


下图则是u节点存在的情况

c为下面4种情况的
任意一种包含一个黑节点的红黑树
d和e可能是空或者一个红节点

插入新节点,更新完后
继续往后更新
就是情况二的u存在的情况

情况三:
cur为红,p为红,g为黑
u不存在或u存在且为黑
跟情况二完全类似
只是情况三为双旋
情况二是单旋
p为g的左孩子,cur为p的右孩子
则针对p做左单旋转
相反
p为g的右孩子,cur为p的左孩子
则针对p做右单旋转
则转换成了情况2
此图为u不存在
u存在参考情况二
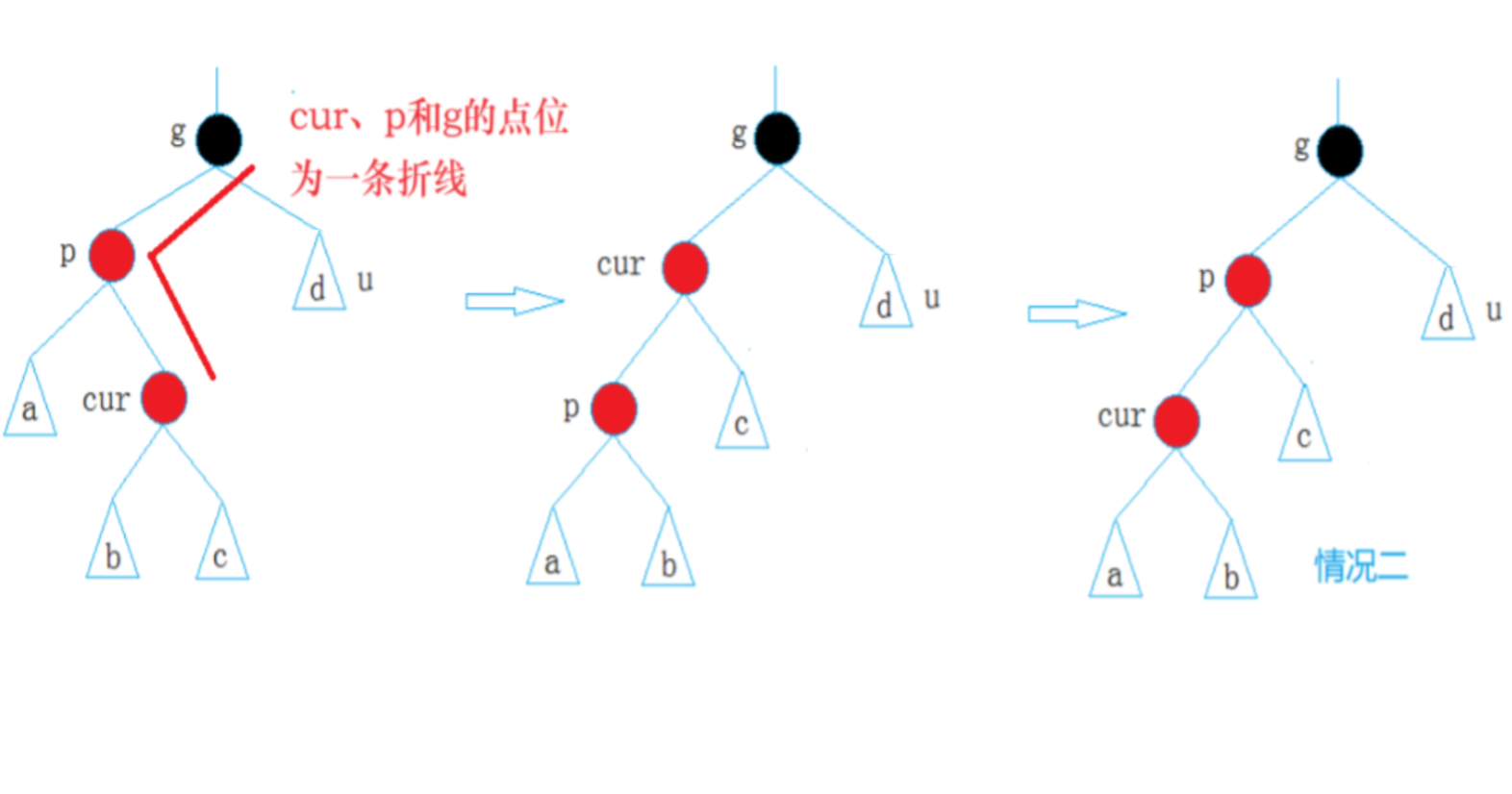
四、红黑树插入代码的全部实现
详解都在代码注释
各位友友们请耐心看完
bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first) // 插入节点比当前节点大往右走, 小往左走{parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}// 链接cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}// new的节点的parent还指向空cur->_parent = parent;// 如果新插入节点破坏了红黑树规则// 则更新节点颜色while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (grandfather->_left == parent){Node* uncle = grandfather->_right;// 情况1:u存在且为红,变色处理,并继续往上处理if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 继续往上调整cur = grandfather;parent = cur->_parent;}else // 情况2+3:u不存在或者u存在且为黑,旋转+处理{// 如果插入节点在父节点的左,c、p、g呈一条斜线// g// p u// cif (parent->_left == cur){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED; }else{// 插入节点在父节点的右,c、p、g呈一条折线// g// p u// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;// parent->_col = RED; // 父亲本就是红,变一下双重保险grandfather->_col = RED;}break;}}else // (grandfather->_right == parent){Node* uncle = grandfather->_left;// 情况1:u存在且为红,变色处理,并继续往上处理if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 继续往上调整cur = grandfather;parent = cur->_parent;}else // 情况2+3:u不存在或者u存在且为黑,旋转+处理{// g// u p// cif (parent->_right == cur){RotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{// g// u p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK; // 做个双保险,无论那种情况把根都变成黑的return true;
}
五、红黑树全部代码模拟实现
gitee链接
✨✨✨✨✨✨✨✨
本篇博客完,感谢阅读🌹
如有错误之处可评论指出
博主会耐心听取每条意见
✨✨✨✨✨✨✨✨
相关文章:

【C++进阶06】红黑树图文详解及C++模拟实现红黑树
一、红黑树的概念及性质 1.1 红黑树的概念 AVL树用平衡因子让树达到高度平衡 红黑树可以认为是AVL树的改良 通过给每个节点标记颜色让树接近平衡 以减少树在插入节点的旋转 在每个结点新增一个存储位表示结点颜色 可以是Red或Black 通过对任何一条从根到叶子的路径上 各个结点…...

2023年最严重的10起0Day漏洞攻击事件
根据谷歌公司威胁分析小组去年 7 月发布的报告显示,2022 年全球共有 41 个 0day 漏洞被利用和披露。而研究人员普遍认为,2023 年被利用的 0Day 漏洞数量会比 2022 年更高,这些危险的漏洞被广泛用于商业间谍活动、网络攻击活动以及数据勒索攻击…...

Linux之Iptables简易应用
文档形成时期:2009-2024年 和iptables打交道有15年了,经过无数实践后,形成一个简易应用文档。 文档主题是简易应用,所以其原理不详述了。 因软件世界之复杂和个人能力之限,难免疏漏和错误,欢迎指正。 文章目…...

树状结构查询 - 华为OD统一考试
OD统一考试 分值: 200分 题解: Java / Python / C++ 题目描述 通常使用多行的节点、父节点表示一棵树,比如: 西安 陕西 陕西 中国 江西 中国 中国 亚洲 泰国 亚洲 输入一个节点之后,请打印出来树中他的所有下层节点。 输入描述 第一行输入行数,下面是多行数据,每行以…...
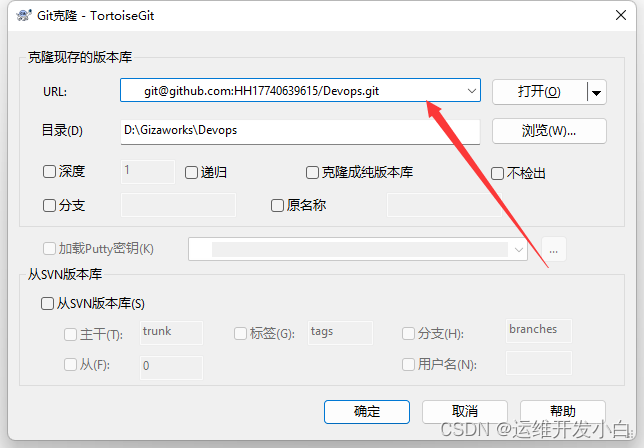
版本控制系统教程
1.Git的基本介绍 1.1 Git的概念 Git是一个开源的分布式版本控制系统,用于敏捷高效地处理任何或小或大的项目.Git是Linus Torvalds为了帮助管理Linux内核开发而开发的一个开放源码的版本控制软件.Git与常用的版本控制工具CVS,Subversion等不同ÿ…...

Java多线程并发篇----第十篇
系列文章目录 文章目录 系列文章目录前言一、start 与 run 区别二、JAVA 后台线程三、什么是乐观锁前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这篇文章男女通用,看懂了就去分享给你的码吧。 一、start 与 r…...

模型\视图一般步骤:为什么经常要用“选择模型”QItemSelectionModel?
一、“使用视图”一般的步骤: //1.创建 模型(这里是数据模型!) tabModelnew QSqlTableModel(this,DB);//数据表 //2.设置 视图的模型(这里是数据模型!) ui->tableView->setModel(tabModel); 模型种类: QStringListModel…...
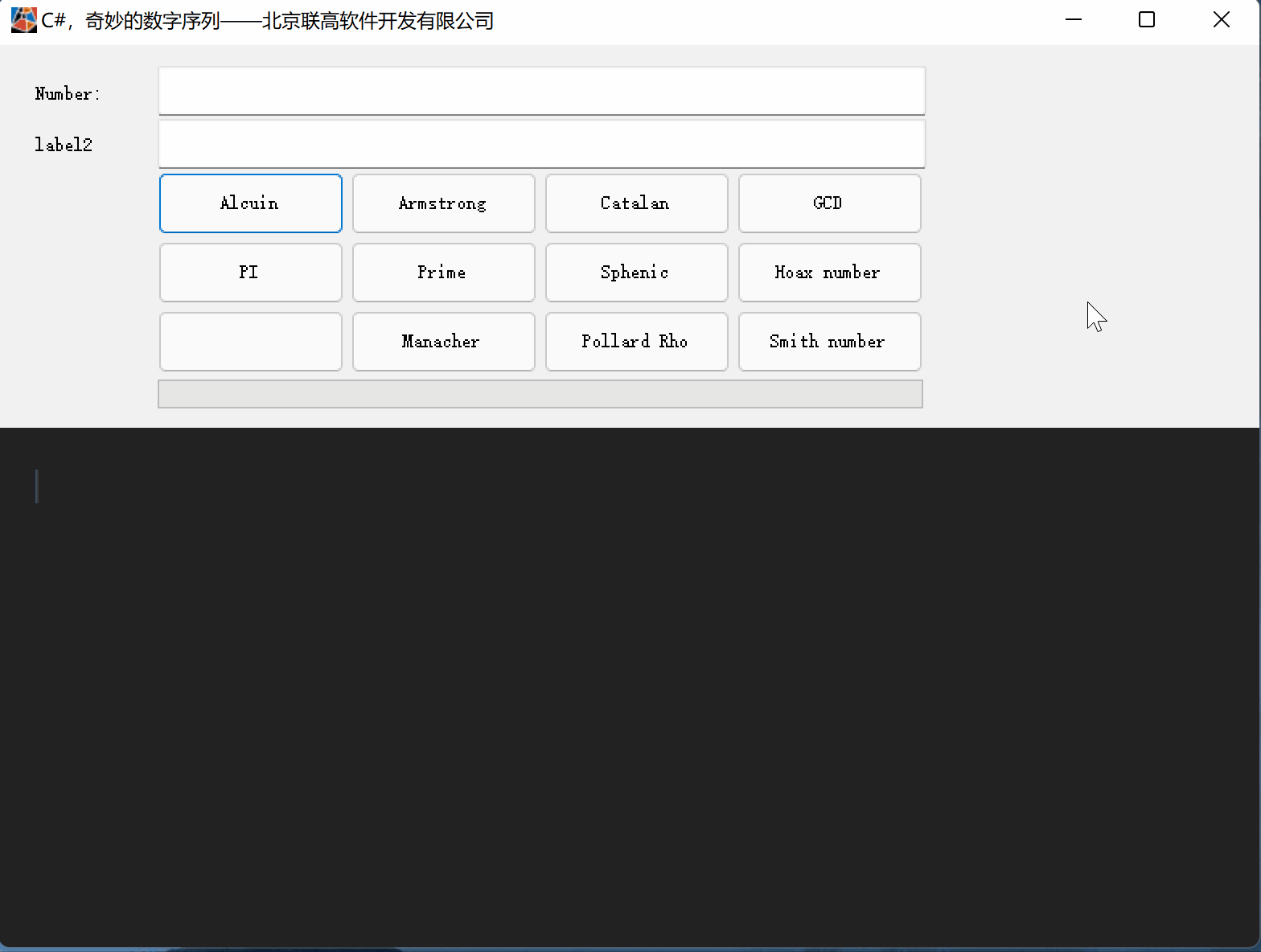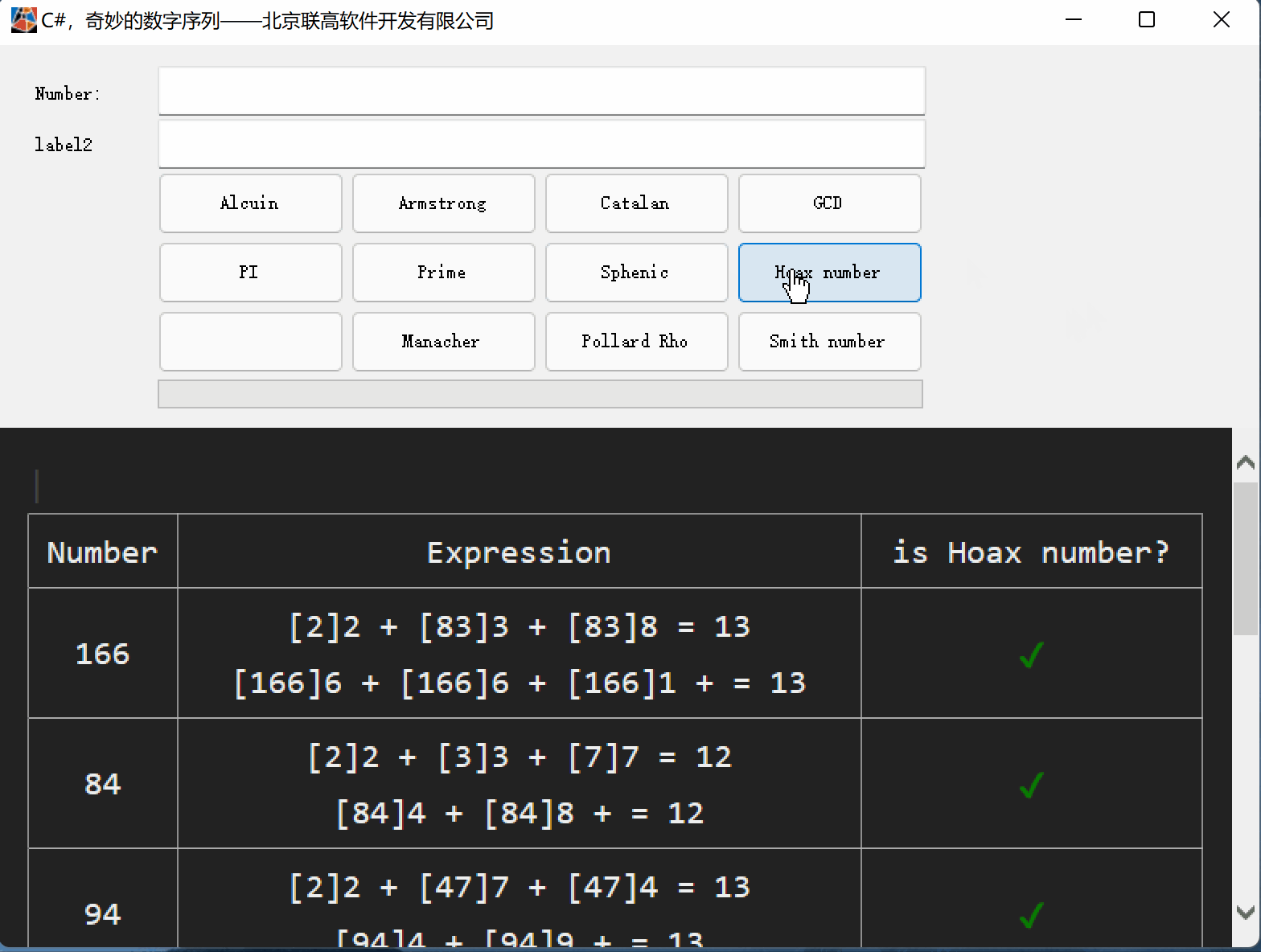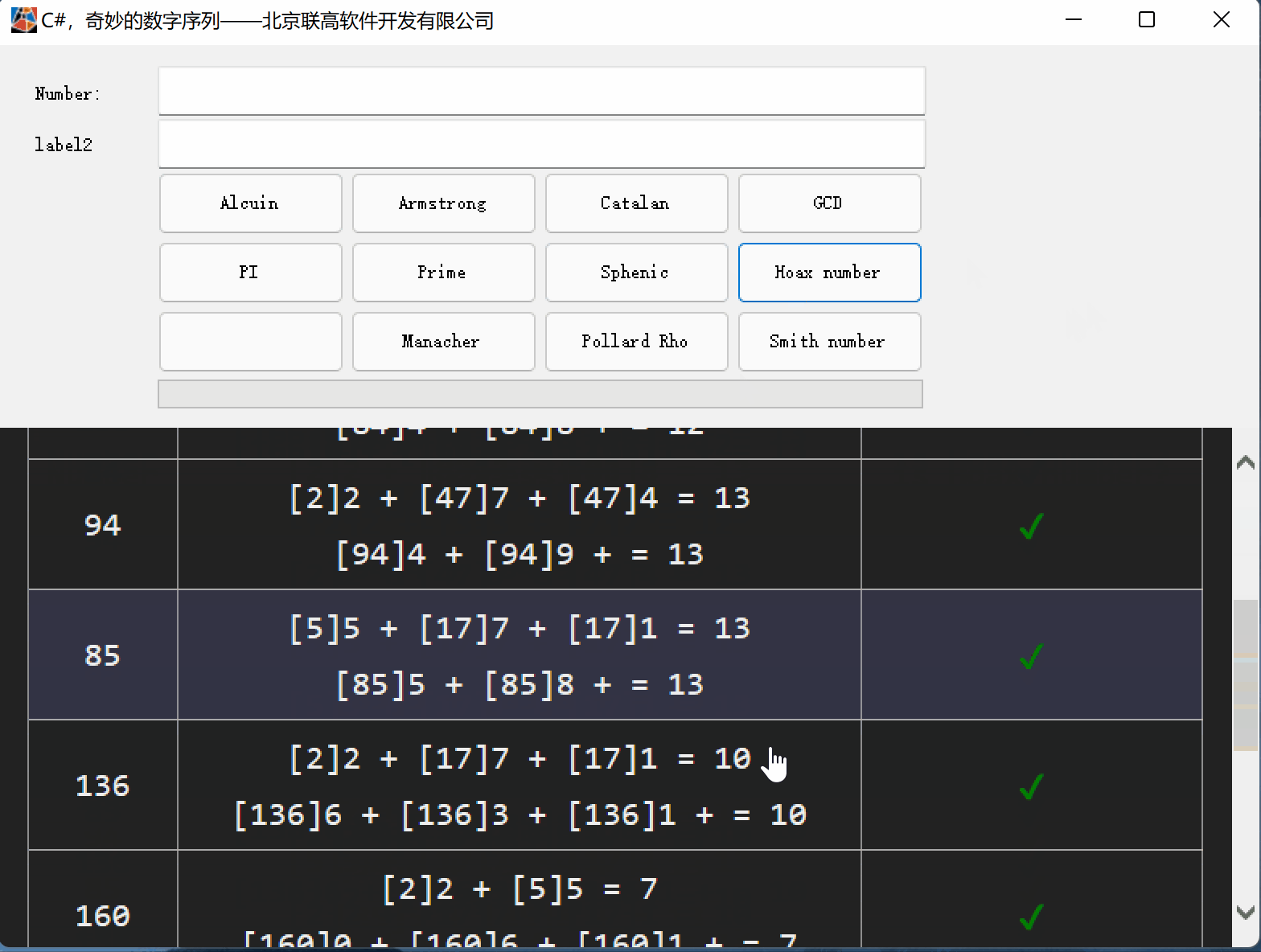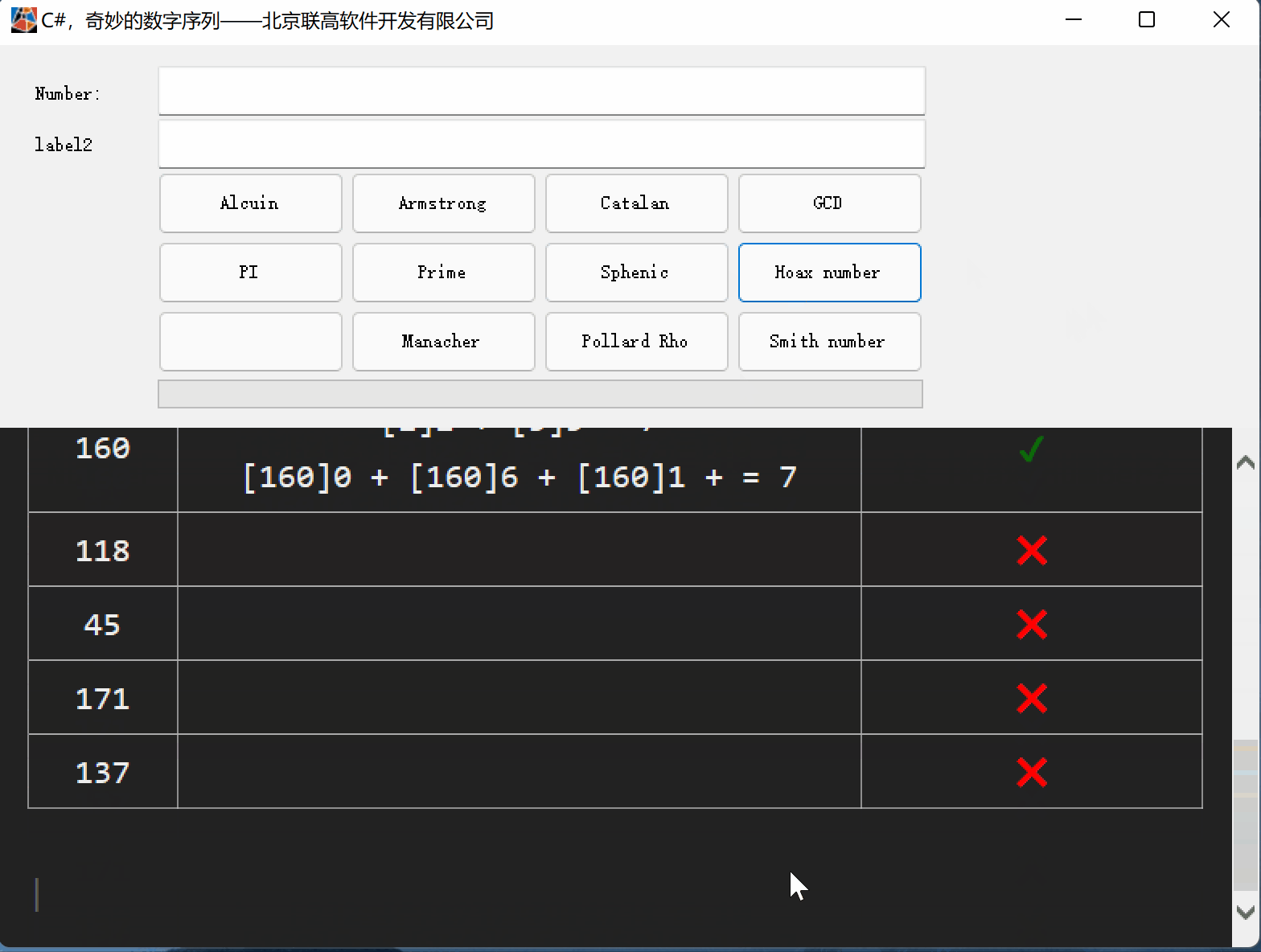
C#,愚弄数(Hoax Number)的计算方法与源代码
一、愚弄数(Hoax Number) 愚弄数(Hoax Number)是一种组合数字, 其数字总和等于其不同质因数的数字总和。 注:1不被视为质数, 因此它不包含在不同质因数的总和中。 有些愚弄数(Hoax Number)数字也…...

c JPEG编码,此程序没有处现MCU中亮度分量的排序
#include <stdio.h> #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #include <stdlib.h> #include <unistd.h> #include <sys/ioctl.h> #include <linux/videodev2.h> //v4l2 头文件 #include <strin…...
前端规范扩展
前端编程规范是基于原有vue2基础上那套《编码风格及标准》上,应用于vue3、typescript、vite2基础上延伸出来的扩展补充,持续完善 一、编码规范 ESLint 代码检测工具 Pretter 代码格式化工具配合双校验代码 Git 规范 - 编码工具 vscode 同步参考文档中…...

【AI视野·今日NLP 自然语言处理论文速览 第七十二期】Mon, 8 Jan 2024
AI视野今日CS.NLP 自然语言处理论文速览 Mon, 8 Jan 2024 Totally 17 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers DeepSeek LLM: Scaling Open-Source Language Models with Longtermism Authors DeepSeek AI Xiao Bi, Deli Ch…...

RT-Thread基于AT32单片机的CAN应用
1 硬件电路 2 RT-Thread驱动配置 RT-Studio中没有CAN相关的图形配置,需要手动修改board.h。在board.h的末尾,增加相关的BSP配置。 #define RT_CAN_USING_HDR #define BSP_USING_CAN13 IO配置 at32_msp.c中的IO配置是PB9和PB10,掌上实验室V…...

LeetCode---121双周赛---数位dp
题目列表 2996. 大于等于顺序前缀和的最小缺失整数 2997. 使数组异或和等于 K 的最少操作次数 2998. 使 X 和 Y 相等的最少操作次数 2999. 统计强大整数的数目 一、大于等于顺序前缀和的最小缺失整数 简单的模拟题,只要按照题目的要求去写代码即可,…...

RT-Thread I/O设备模型
I/O设备模型 绝大部分的嵌入式系统都包括一些I/O(Input/Output,输入/输出)设备,例如仪器上的数据显示屏、工业设备上的串口通信、数据采集设备上用于保存数据的Flash或SD卡,以及网络设备的以太网接口等,都…...

CloudCompare——拟合空间球
目录 1.拟合球2.软件操作3.算法源码4.相关代码 本文由CSDN点云侠原创,CloudCompare——拟合空间球,爬虫自重。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫与GPT生成的文章。 1.拟合球 源码里用到了四点定球,…...

哪个牌子的护眼台灯适合学生?2024护眼台灯推荐
不知道各位父母对孩子的视力健康有没有关注,我国儿童青少年的近视率高达52.7%,也就是说,平均是个儿童中就有五个儿童存在视力问题,而且近视发生年龄提前至3到7岁。作为一名眼部护理博主,孩子从小看书、看屏幕起&#x…...

适用于动态 IT 环境的服务器流量监控软件
服务器在网络性能中起着至关重要的作用,这意味着保持其最佳容量至关重要。企业需要将 AI、ML 和云技术融入其 IT 中,从而提供充分的敏捷性、安全性和灵活性,在这方面,服务器流量监控已成为当务之急。通过定期监控通信、跟踪流量上…...

Java的Jar包和War包
在Java中,JAR(Java Archive)和WAR(Web Archive)都是用于打包和分发Java应用程序的压缩文件格式。它们在不同的应用场景中使用: JAR(Java Archive): 用途: 主要…...
)
第二十一章 javascript数据代理(数据劫持)
文章目录 一、数据劫持对象的访问器属性 二、Object.defineProperty()三、Proxy()四、补充1. Object类新增方法2. Array类新增方法 一、数据劫持 数据劫持:能够拦截到数据被使用或被修改的时机,在这个时机除了可以获取数据的值或对数据的值进行修改之外…...
苹果电脑RAW图像处理软件Capture One Pro 22 mac软件介绍
Capture One Pro 22 for mac是一款专业的RAW文件转换器和图像编辑软件,拥有更新的处理引擎、市场领先的性能和强大的新功能,可为 500 多台高端相机提供具有美丽色彩和令人难以置信的细节的终极图像质量。 Capture One Pro 22 for Mac版软件介绍 Capture…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
