LeetCode---121双周赛---数位dp
题目列表
2996. 大于等于顺序前缀和的最小缺失整数
2997. 使数组异或和等于 K 的最少操作次数
2998. 使 X 和 Y 相等的最少操作次数
2999. 统计强大整数的数目
一、大于等于顺序前缀和的最小缺失整数

简单的模拟题,只要按照题目的要求去写代码即可,代码如下
class Solution {
public:int missingInteger(vector<int>& nums) {int i=1,ans=nums[0],n=nums.size();while(i<n){if(nums[i]-nums[i-1]!=1)break;ans+=nums[i];i++;}unordered_set<int>s(nums.begin(),nums.end());while(s.count(ans))ans++;return ans;}
};二、使数组异或和为K的最小操作次数

这题考异或的性质---相同为0,相异为1,我们只要关心nums的异或和与K的二进制位有几个不同即可,也就是将k和nums一起异或,最后看二进制位上还有几个1
(这里可能有人还是很懵,简单说一下思路的正确性,异或运算的性质决定了它不会干扰到其他位,我们可以把异或运算看作是每个二进制位的单独的运算且满足交换律,现在我们单独看某一个二进制位,如果共有3个1,2个0异或,那么异或结果为1,如果我们将其中的一个1换成0或者将一个0换成1,异或的结果就会改变,至于被修改的是哪个数字的二进制位无所谓都行,所以二进制位的单一位,只需进行一次操作就能发生改变,所以我们的答案如上诉所说)
代码如下
class Solution {
public:int minOperations(vector<int>& nums, int k) {for(auto&e:nums)k^=e;return __builtin_popcount(k);//求二进制位上的1的个数}
};三、使X和Y相等的最小操作次数

这题有两种思路,都给大家讲一讲,在讲思路之前,我们都应该能观察得到,当x<=y时,我们只能用+1操作,即操作个数一定为y-x,也就是说我们只要考虑x>y的情况
思路一:图的bfs
我们将x->y过程中经过的每个数看作是图上的结点,然后我们用层序遍历的思路一层层往外遍历,直到我们找到y,返回结果,因为我们的操作次数是累加的,所以第一次找到y时我们一定能得到最小的操作次数(不代表层序遍历的次数就是最小操作次数,也可能出现操作后的数小于y,然后通过+1操作实现=y的情况,具体看代码)。这个思路的关键是你能想到它能用图来类比,从而想到层序遍历,当然实现细节还是很多的。
(启发:图的遍历不是只有图能用,像这种抽象的,从一个"点"到另一个"点",且中间经过的"点"是确定的,然后要求最小操作次数,就可以往图的层序遍历去思考)
代码如下
class Solution {
public:int minimumOperationsToMakeEqual(int x, int y) {if(x<=y)return y-x;int ans=x-y;//代表操作上限(只用减法)//ans+x是在操作上限的范围内只做加法操作的最大数字,+1是因为下标vector<bool>vis(ans+x+1);//记录遍历到的结点,能减少重复数字的遍历次数int step=0;vector<int>q;auto add=[&](int v){if(v<y)ans=min(ans,step+1+y-v);else if(!vis[v]){vis[v]=true;q.push_back(v);}};add(x);while(1){auto tmp=q;q.clear();for(auto v:tmp){if(v==y)return min(ans,step);if(v%5==0)add(v/5);if(v%11==0)add(v/11);add(v-1);add(v+1);}step++;}}
};思路二:记忆化搜索
首先我们要对递归有一个大体的方向,由于我们只考虑x>y的情况,所以要求操作次数最少,我们肯定希望尽可能的用/5 、/11,让x能快速的接近y,即我们将加减1当作辅助操作,同时还要考虑到只用减法操作得到最小操作次数的情况。
我们根据题意,确定递归的参数和返回值,dfs(v)返回从v到y的最小操作次数
接下来我们来想想如何从v->y
1、v<=y,只能进行+1操作,操作次数为v-y,直接返回
2、v>y
1)只用减法操作,操作次数为v-y
2)用/5操作,两种可能,进行v%5次减法操作,或者进行5-v%5次加法操作,让v变成5的倍数后/5,操作次数为min(dfs(v/5)+v%5,dfs(v/5+1)+5-v%5)+1,+1是因为/5也要算操作次数
3)用/11操作,两种可能,进行v%11次减法操作,或者进行11-v%11次加法操作,让v变成11的倍数后/11,操作次数为min(dfs(v/11)+v%11,dfs(v/11+1)+11-v%11)+1
返回三者的最小值
对于v>y的后两种情况,我们是根据红字部分得来的,其实并不严谨,因为我们没有证明,v到它前后最近的5的倍数是最优解,即它再+5/-5得到的另一个5的倍数是否会更好?这个其实很好想,+5/-5的操作次数导致的结果就是/5之后的数字相差了一个1,那么我先/5后再+1/-1,不是能更快得到结果嘛(11同理),所以我们只考虑v前后的5的倍数即可,代码如下
class Solution {
public:int minimumOperationsToMakeEqual(int x, int y) {if(x<=y)return y-x;int memo[x+1];memset(memo,-1,sizeof(memo));function<int(int)>dfs=[&](int v)->int{if(v<=y)return y-v;if(memo[v]!=-1) return memo[v];int res=v-y;res=min(res,min(dfs(v/5)+v%5,dfs(v/5+1)+5-v%5)+1);res=min(res,min(dfs(v/11)+v%11,dfs(v/11+1)+11-v%11)+1);return memo[v]=res;};return dfs(x);}
};四、统计强大整数的数目

这题很典型的数位dp题,要求我们返回在所给范围内的满足条件的数字个数。数位dp的思路就是考虑如何构造出这样一个符合要求的数字,我们一位一位的考虑即可。
代码如下
class Solution {typedef long long LL;
public:long long numberOfPowerfulInt(long long start, long long finish, int limit, string s) {//将数字区间端点变成字符串string left=to_string(start);string right=to_string(finish);int n=right.size();left=string(n-left.size(),'0')+left;//补上前导零,方便后面的计算int diff=n-s.size();//记忆化搜索vector<LL>memo(n,-1);function<LL(int,bool,bool)>dfs=[&](int i,bool limit_low,bool limit_high)->LL{if(i==n)//递归到这,说明构造的数字合法,返回1return 1;if(!limit_high&&!limit_low&&memo[i]!=-1) //这个是因为限制高/限低在递归中只会走一次,没有必要进行记忆化,所以记忆数组可以是一维的return memo[i];//求当前位置的数的取值范围int high=limit_high?right[i]-'0':9;int low=limit_low?left[i]-'0':0;LL res=0;//根据题目的其他限制条件,进行递归if(i<diff)for(int d=low;d<=min(high,limit);d++)res+=dfs(i+1,d==low&&limit_low,d==high&&limit_high);else{int d=s[i-diff]-'0';if(d>=low&&d<=min(high,limit))res=dfs(i+1,d==low&&limit_low,d==high&&limit_high);}if(!limit_high&&!limit_low)memo[i]=res;return res;};return dfs(0,true,true);}
};相关文章:

LeetCode---121双周赛---数位dp
题目列表 2996. 大于等于顺序前缀和的最小缺失整数 2997. 使数组异或和等于 K 的最少操作次数 2998. 使 X 和 Y 相等的最少操作次数 2999. 统计强大整数的数目 一、大于等于顺序前缀和的最小缺失整数 简单的模拟题,只要按照题目的要求去写代码即可,…...

RT-Thread I/O设备模型
I/O设备模型 绝大部分的嵌入式系统都包括一些I/O(Input/Output,输入/输出)设备,例如仪器上的数据显示屏、工业设备上的串口通信、数据采集设备上用于保存数据的Flash或SD卡,以及网络设备的以太网接口等,都…...

CloudCompare——拟合空间球
目录 1.拟合球2.软件操作3.算法源码4.相关代码 本文由CSDN点云侠原创,CloudCompare——拟合空间球,爬虫自重。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫与GPT生成的文章。 1.拟合球 源码里用到了四点定球,…...

哪个牌子的护眼台灯适合学生?2024护眼台灯推荐
不知道各位父母对孩子的视力健康有没有关注,我国儿童青少年的近视率高达52.7%,也就是说,平均是个儿童中就有五个儿童存在视力问题,而且近视发生年龄提前至3到7岁。作为一名眼部护理博主,孩子从小看书、看屏幕起&#x…...

适用于动态 IT 环境的服务器流量监控软件
服务器在网络性能中起着至关重要的作用,这意味着保持其最佳容量至关重要。企业需要将 AI、ML 和云技术融入其 IT 中,从而提供充分的敏捷性、安全性和灵活性,在这方面,服务器流量监控已成为当务之急。通过定期监控通信、跟踪流量上…...

Java的Jar包和War包
在Java中,JAR(Java Archive)和WAR(Web Archive)都是用于打包和分发Java应用程序的压缩文件格式。它们在不同的应用场景中使用: JAR(Java Archive): 用途: 主要…...
)
第二十一章 javascript数据代理(数据劫持)
文章目录 一、数据劫持对象的访问器属性 二、Object.defineProperty()三、Proxy()四、补充1. Object类新增方法2. Array类新增方法 一、数据劫持 数据劫持:能够拦截到数据被使用或被修改的时机,在这个时机除了可以获取数据的值或对数据的值进行修改之外…...
苹果电脑RAW图像处理软件Capture One Pro 22 mac软件介绍
Capture One Pro 22 for mac是一款专业的RAW文件转换器和图像编辑软件,拥有更新的处理引擎、市场领先的性能和强大的新功能,可为 500 多台高端相机提供具有美丽色彩和令人难以置信的细节的终极图像质量。 Capture One Pro 22 for Mac版软件介绍 Capture…...
phpcms v9后台添加草稿箱功能
一、后台添加文章模板phpcms/modules/content/templates/content_add.tpl.php中94行增加”保存草稿“按钮: <div class"button"><input value"<?php echo L(save_draft);?>" type"submit" name"dosubmit_draf…...

机器人持续学习基准LIBERO系列5——获取显示深度图
0.前置 机器人持续学习基准LIBERO系列1——基本介绍与安装测试机器人持续学习基准LIBERO系列2——路径与基准基本信息机器人持续学习基准LIBERO系列3——相机画面可视化及单步移动更新机器人持续学习基准LIBERO系列4——robosuite最基本demo 1.更改环境设置 LIBERO-master/l…...

Java 面试题 - 多线程并发篇
线程基础 创建线程有几种方式 继承Thread类 可以创建一个继承自Thread类的子类,并重写其run()方法来定义线程的行为。然后可以通过创建该子类的实例来启动线程。 示例代码: class MyThread extends Thread {public void run() {// 定义线程的行为} …...

2401d,讨论d串滑动参数
原文 因为对编译时执行的i串的兴趣,我一直在考虑搞个通用用例,而不是相关i串的用例. 滑动模板参数 请考虑以下模板: void pluto(string s)() {pragma(msg, s); } void test() {pluto!"hello"(); }因为s是编译时参数,这编译,而pragma(msg,s) 期望s为编译时值. voi…...

etcd官方docker镜像及dockerfile问题处理
解决下我之前etcd使用docker镜像启动的坑 1、问题镜像docker-file: 这个dockerfile看着看不出来问题,但如果有人真的执行我之前两篇文章的文件,就会有问题,什么问题呢,无法连接到etcd,由于我是刚装上docker,排查了一圈,包括docker网络及是否是本地docker的网络问题,…...

2023 IoTDB Summit:天谋科技高级开发工程师苏宇荣《汇其流:如何用 IoTDB 流处理框架玩转端边云融合》...
12 月 3 日,2023 IoTDB 用户大会在北京成功举行,收获强烈反响。本次峰会汇集了超 20 位大咖嘉宾带来工业互联网行业、技术、应用方向的精彩议题,多位学术泰斗、企业代表、开发者,深度分享了工业物联网时序数据库 IoTDB 的技术创新…...
Pygame程序的屏幕显示
不同对象的绘制与显示过程 在Pygame中,需要将所有需要在屏幕上显示的内容都绘制在一个display surface上。该Surface通常称为screen surface,它是pygame.display.set_mode()函数返回的Surface对象。 在绘制不同对象时,可以使用不同的绘制方…...
LVGL的List控件的触摸按键和实体按键的处理
在LVGL的List控件使用过程中,虽然通过触摸按键选择item,但是有些场景需要实体按键选取item,但是LVGL 的V8.3中没有像Emwin那样有函数选择list item的函数。LVGL中List引入了Group的概念,把列表项都添加到同一个group中。然后通过更…...
数据结构 模拟实现二叉树(孩子表示法)
目录 一、二叉树的简单概念 (1)关于树的一些概念 (2)二叉树的一些概念及性质 定义二叉树的代码: 二、二叉树的方法实现 (1)createTree (2)preOrder (…...

Android14之解决刷机报错:Can not load Android system. Your data may be corrupt(一百七十七)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...

二阶贝塞尔曲线生成弧线
概述 本文分享一个二阶贝塞尔曲线曲线生成弧线的算法。 效果 实现 1. 封装方法 class ArcLine {constructor(from, to, num 100) {this.from from;this.to to;this.num num;return this.getPointList();}getPointList() {const { from, to } thisconst ctrlPoint thi…...
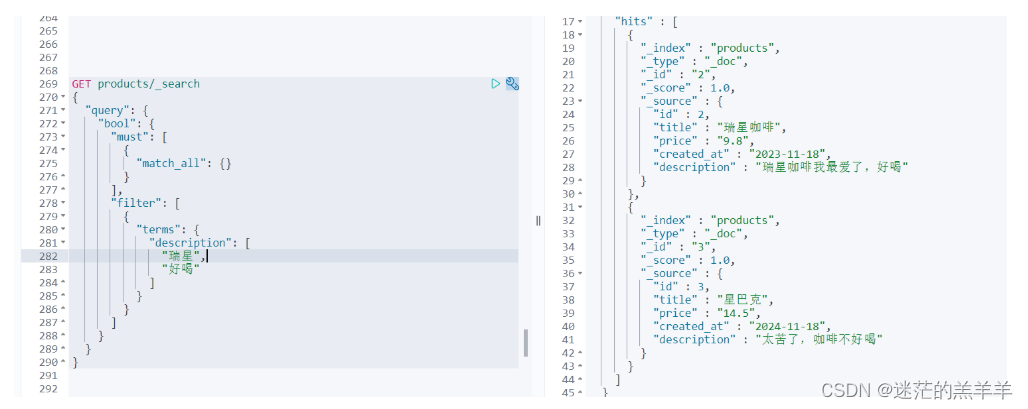
FilterQuery过滤查询
ES中的查询操作分为两种:查询和过滤。查询即是之前提到的query查询,它默认会计算每个返回文档的得分,然后根据得分排序。而过滤只会筛选出符合条件的文档,并不计算得分,并且可以缓冲记录。所以我们在大范围筛选数据时&…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

前端工具库lodash与lodash-es区别详解
lodash 和 lodash-es 是同一工具库的两个不同版本,核心功能完全一致,主要区别在于模块化格式和优化方式,适合不同的开发环境。以下是详细对比: 1. 模块化格式 lodash 使用 CommonJS 模块格式(require/module.exports&a…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...

npm安装electron下载太慢,导致报错
npm安装electron下载太慢,导致报错 背景 想学习electron框架做个桌面应用,卡在了安装依赖(无语了)。。。一开始以为node版本或者npm版本太低问题,调整版本后还是报错。偶尔执行install命令后,可以开始下载…...

【Redis】Redis从入门到实战:全面指南
Redis从入门到实战:全面指南 一、Redis简介 Redis(Remote Dictionary Server)是一个开源的、基于内存的键值存储系统,它可以用作数据库、缓存和消息代理。由Salvatore Sanfilippo于2009年开发,因其高性能、丰富的数据结构和广泛的语言支持而广受欢迎。 Redis核心特点:…...
