【蓝桥杯软件赛 零基础备赛20周】第7周——二叉树
文章目录
- 1 二叉树概念
- 2 二叉树的存储和编码
- 2.1 二叉树的存储方法
- 2.2 二叉树存储的编码实现
- 2.3 二叉树的极简存储方法
- 3 例题
- 4 习题
前面介绍的数据结构数组、队列、栈,都是线性的,它们存储数据的方式是把相同类型的数据按顺序一个接一个串在一起。简单的形态使线性表难以实现高效率的操作。
二叉树是一种层次化的、高度组织性的数据结构。二叉树的形态使得它有天然的优势,在二叉树上做查询、插入、删除、修改、区间等操作极为高效,基于二叉树的算法也很容易实现高效率的计算。
1 二叉树概念
二叉树的每个节点最多有两个子节点,分别称为左孩子、右孩子,以它们为根的子树称为左子树、右子树。二叉树的每一层以2的倍数递增,所以二叉树的第k层最多有 2 k − 1 2^{k-1} 2k−1 个节点。根据每一层的节点分布情况,有以下常见的二叉树。
(1)满二叉树
特征是每一层的节点数都是满的。第一层只有1个节点,编号为1;第二层有2个节点,编号2、3;第三层有4个节点,编号4、5、6、7;…;第k层有 2 k − 1 2^{k-1} 2k−1 个节点,编号 2 k − 1 2^{k-1} 2k−1、 2 k − 1 + 1 2^{k-1}+1 2k−1+1、…、 2 k − 1 2^k-1 2k−1。
一棵n层的满二叉树,节点一共有 1 + 2 + 4 + . . . + 2 n − 1 = 2 n − 1 1+2+4+...+2^{n-1} = 2^{n-1} 1+2+4+...+2n−1=2n−1 个。
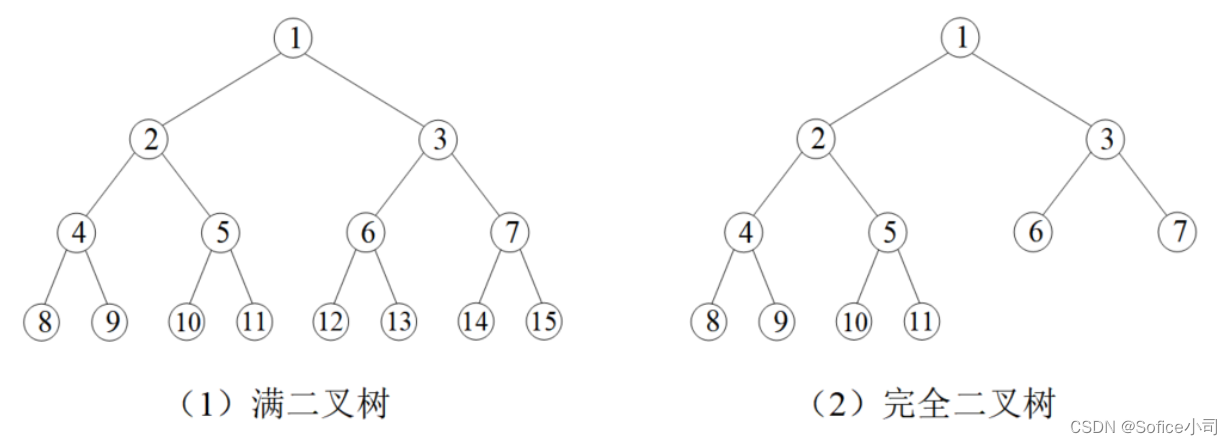
(2)完全二叉树
如果满二叉树只在最后一层有缺失,并且缺失的节点都在最后,称为完全二叉树。上图演示了一棵满二叉树和一棵完全二叉树。
(3)平衡二叉树
任意左子树和右子树的高度差不大于1,称为平衡二叉树。若只有少部分子树的高度差超过1,这是一棵接近平衡的二叉树。
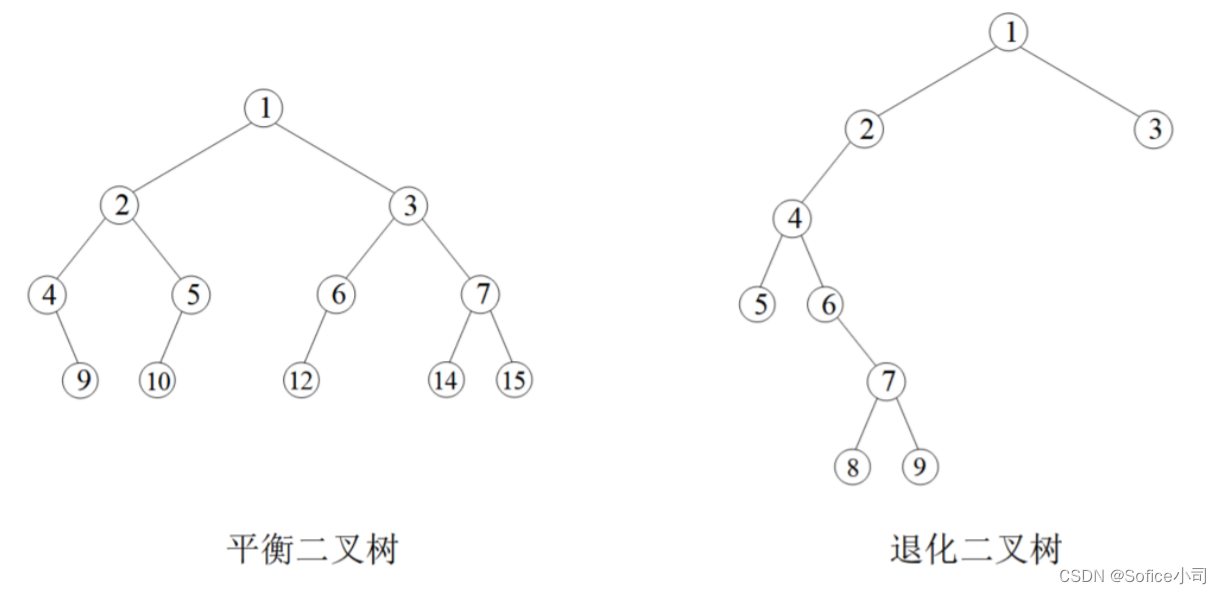
(4)退化二叉树
如果树上每个节点都只有1个孩子,称为退化二叉树。退化二叉树实际上已经变成了一根链表。如果绝大部分节点只有1个孩子,少数有2个孩子,也看成退化二叉树。
二叉树之所以应用广泛,得益于它的形态。高级数据结构大部分和二叉树有关,下面列举二叉树的一些优势。
(1)在二叉树上能进行极高效率的访问。一棵平衡的二叉树,例如满二叉树或完全二叉树,每一层的节点数量约是上一层数量的2倍,也就是说,一棵有N个节点的满二叉树,树的高度是O(logN)。从根节点到叶子节点,只需要走logN步,例如N = 100万,树的高度仅有logN = 20,只需要20步就能到达100万个节点中的任意一个。但是,如果二叉树不是满的,而且很不平衡,甚至在极端情况下变成退化二叉树,访问效率会打折扣。维护二叉树的平衡是高级数据结构的主要任务之一。
(2)二叉树很适合做从整体到局部、从局部到整体的操作。二叉树内的一棵子树可以看成整棵树的一个子区间,求区间最值、区间和、区间翻转、区间合并、区间分裂等,用二叉树都很快捷。
(3)基于二叉树的算法容易设计和实现。例如二叉树用BFS和DFS搜索处理都极为简便。二叉树可以一层一层地搜索,这是BFS。二叉树的任意一个子节点,是以它为根的一棵二叉树,这是一种递归的结构,用DFS访问二叉树极容易编码。
2 二叉树的存储和编码
2.1 二叉树的存储方法
要使用二叉树,首先得定义和存储它的节点。
二叉树的一个节点包括三个值:节点的值、指向左孩子的指针、指向右孩子的指针。需要用一个结构体来定义二叉树。
二叉树的节点有动态和静态两种存储方法,竞赛中一般采用静态方法。
(1)动态存储二叉树。例如写c代码,数据结构的教科书一般这样定义二叉树的节点:
struct Node{int value; //节点的值,可以定义多个值Node *lson, *rson; //指针,分别指向左右子节点
};
其中value是这个节点的值,lson和rson是指向两个孩子的指针。动态新建一个Node时,用new运算符动态申请一个节点。使用完毕后,需要用delete释放它,否则会内存泄漏。动态二叉树的优点是不浪费空间,缺点是需要管理,不小心会出错,竞赛中一般不这样用。
(2)用静态数组存储二叉树。在算法竞赛中,为了编码简单,加快速度,一般用静态数组来实现二叉树。下面定义一个大小为N的结构体数组。N的值根据题目要求设定,有时节点多,例如N=100万,那么tree[N]使用的内存是12M字节,不算大。
struct Node{ //静态二叉树int value; //可以把value简写为vint lson, rson; //左右孩子,可以把lson、rson简写为ls、rs
}tree[N]; //可以把tree简写为t
tree[i]表示这个节点存储在结构体数组的第i个位置,lson是它的左孩子在结构体数组的位置,rson是它的右孩子在结构体数组的位置。lson和rson指向孩子的位置,也可以称为指针。
下图演示了一棵二叉树的存储,圆圈内的字母是这个节点的value值。根节点存储在tree[5]上,它的左孩子lson=7,表示左孩子存储在tree[7]上,右孩子rson=3,存储在tree[3]。
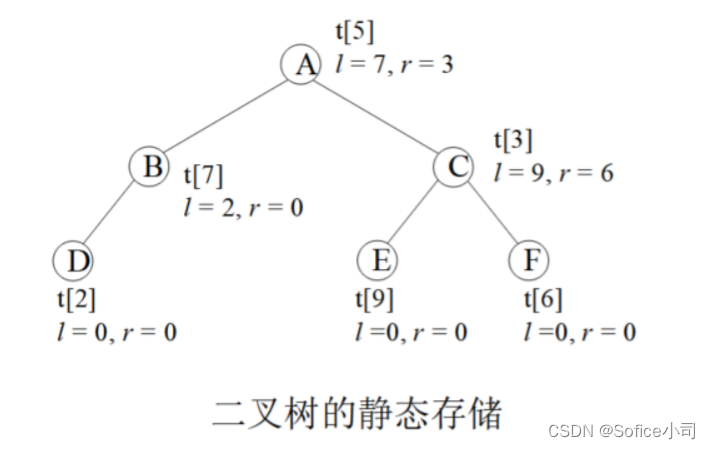
编码时一般不用tree[0],因为0常常被用来表示空节点,例如叶子节点tree[2]没有子节点,就把它的子节点赋值为lson = rson = 0。
2.2 二叉树存储的编码实现
下面写代码演示上图中二叉树的建立,并输出二叉树。
(1)C++代码。第16~21行建立二叉树,然后用print_tree()输出二叉树。
#include <bits/stdc++.h>
using namespace std;
const int N=100; //注意const不能少
struct Node{ //定义静态二叉树结构体char v; //把value简写为vint ls, rs; //左右孩子,把lson、rson简写为ls、rs
}t[N]; //把tree简写为t
void print_tree(int u){ //打印二叉树if(u){cout<<t[u].v<<' '; //打印节点u的值print_tree(t[u].ls); //继续搜左孩子print_tree(t[u].rs); //继续搜右孩子}
}
int main(){t[5].v='A'; t[5].ls=7; t[5].rs=3;t[7].v='B'; t[7].ls=2; t[7].rs=0;t[3].v='C'; t[3].ls=9; t[3].rs=6;t[2].v='D'; // t[2].ls=0; t[2].rs=0; 可以不写,因为t[]是全局变量,已初始化为0t[9].v='E'; // t[9].ls=0; t[9].rs=0; 可以不写t[6].v='F'; // t[6].ls=0; t[6].rs=0; 可以不写int root = 5; //根是tree[5]print_tree(5); //输出: A B D C E Freturn 0;
}
初学者可能看不懂print_tree()是怎么工作的。它是一个递归函数,先打印这个节点的值t[u].v,然后继续搜它的左右孩子。上图的打印结果是”A B D C E F”,步骤如下:
(1)首先打印根节点A;
(2)然后搜左孩子,是B,打印出来;
(3)继续搜B的左孩子,是D,打印出来;
(4)D没有孩子,回到B,B发现也没有右孩子,继续回到A;
(5)A有右孩子C,打印出来;
(6)打印C的左右孩子E、F。
这个递归函数执行的步骤称为“先序遍历”,先输出父节点,然后再搜左右孩子并输出。还有“中序遍历”和“后序遍历”,将在后面讲解。
(2)Java代码
import java.util.*;
class Main {static class Node {char v;int ls, rs;}static final int N = 100;static Node[] t = new Node[N];static void print_tree(int u) {if (u != 0) {System.out.print(t[u].v + " ");print_tree(t[u].ls);print_tree(t[u].rs);}}public static void main(String[] args) {t[5] = new Node(); t[5].v = 'A'; t[5].ls = 7; t[5].rs = 3;t[7] = new Node(); t[7].v = 'B'; t[7].ls = 2; t[7].rs = 0;t[3] = new Node(); t[3].v = 'C'; t[3].ls = 9; t[3].rs = 6;t[2] = new Node(); t[2].v = 'D';t[9] = new Node(); t[9].v = 'E';t[6] = new Node(); t[6].v = 'F';int root = 5;print_tree(5); // 输出: A B D C E F}
}
(3)Python代码
N = 100
class Node: # 定义静态二叉树结构体def __init__(self):self.v = '' # 把value简写为vself.ls = 0 # 左右孩子,把lson、rson简写为ls、rsself.rs = 0
t = [Node() for i in range(N)] # 把tree简写为t
def print_tree(u):if u:print(t[u].v, end=' ') # 打印节点u的值print_tree(t[u].ls)print_tree(t[u].rs)
t[5].v, t[5].ls, t[5].rs = 'A', 7, 3
t[7].v, t[7].ls, t[7].rs = 'B', 2, 0
t[3].v, t[3].ls, t[3].rs = 'C', 9, 6
t[2].v = 'D' # t[2].ls=0; t[2].rs=0; 可以不写,因为t[]已初始化为0
t[9].v = 'E' # t[9].ls=0; t[9].rs=0; 可以不写
t[6].v = 'F' # t[6].ls=0; t[6].rs=0; 可以不写
root = 5 # 根是tree[5]
print_tree(5) # 输出: A B D C E F
2.3 二叉树的极简存储方法
如果是满二叉树或者完全二叉树,有更简单的编码方法,连lson、rson都不需要定义,因为可以用数组的下标定位左右孩子。
一棵节点总数量为k的完全二叉树,设1号点为根节点,有以下性质:
(1) p > 1 p > 1 p>1的节点,其父节点是 ⌊ p / 2 ⌋ \lfloor p/2 \rfloor ⌊p/2⌋。例如 p = 4 p=4 p=4,父亲是 4 / 2 = 2 4/2=2 4/2=2; p = 5 p=5 p=5,父亲是 5 / 2 = 2 5/2=2 5/2=2。
(2)如果 2 × p > k 2×p> k 2×p>k,那么 p p p没有孩子;如果 2 × p + 1 > k 2×p+1 > k 2×p+1>k,那么 p p p没有右孩子。例如 k = 11 k=11 k=11, p = 6 p=6 p=6的节点没有孩子; k = 12 k=12 k=12, p = 6 p=6 p=6的节点没有右孩子。
(3)如果节点 p p p有孩子,那么它的左孩子是 2 × p 2×p 2×p,右孩子是 2 × p + 1 2×p+1 2×p+1。
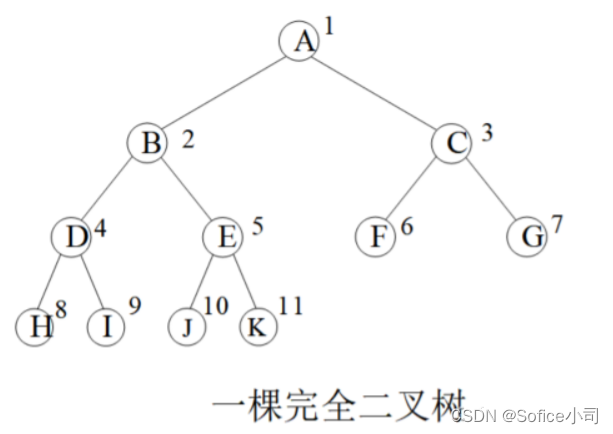
图中圆圈内是节点的值,圆圈外数字是节点存储位置。
(1)C++代码。
用 l s ( p ) ls(p) ls(p)找p的左孩子,用 r s ( p ) rs(p) rs(p)找p的右孩子。 l s ( p ) ls(p) ls(p)中把 p ∗ 2 p*2 p∗2写成 p < < 1 p<<1 p<<1,用了位运算。
#include <bits/stdc++.h>
using namespace std;
const int N=100; //注意const不能少
char t[N]; //简单地用一个数组定义二叉树
int ls(int p){return p<<1;} //定位左孩子,也可以写成 p*2
int rs(int p){return p<<1 | 1;} //定位右孩子,也可以写成 p*2+1
int main(){t[1]='A'; t[2]='B'; t[3]='C';t[4]='D'; t[5]='E'; t[6]='F'; t[7]='G';t[8]='H'; t[9]='I'; t[10]='J'; t[11]='K';cout<<t[1]<<":lson="<<t[ls(1)]<<" rson="<<t[rs(1)]; //输出 A:lson=B rson=Ccout<<endl;cout<<t[5]<<":lson="<<t[ls(5)]<<" rson="<<t[rs(5)]; //输出 E:lson=J rson=Kreturn 0;
}
(2)Java代码。
import java.util.Arrays;
public class Main {static int ls(int p){ return p<<1;}static int rs(int p){ return p<<1 | 1;}public static void main(String[] args) {final int N = 100;char[] t = new char[N];t[1]='A'; t[2]='B'; t[3]='C';t[4]='D'; t[5]='E'; t[6]='F'; t[7]='G';t[8]='H'; t[9]='I'; t[10]='J'; t[11]='K';System.out.print(t[1]+":lson="+t[ls(1)]+" rson="+t[rs(1)]);//输出A:lson=B rson=CSystem.out.println();System.out.print(t[5]+":lson="+t[ls(5)]+" rson="+t[rs(5)]);//输出E:lson=J rson=K}
}
(3)Python代码。
N = 100
t = [''] * N
def ls(p): return p << 1
def rs(p): return (p << 1) | 1t[1] = 'A'; t[2] = 'B'; t[3] = 'C'
t[4] = 'D'; t[5] = 'E'; t[6] = 'F'; t[7] = 'G'
t[8] = 'H'; t[9] = 'I'; t[10] = 'J'; t[11] = 'K'print(t[1] + ':lson=' + t[ls(1)] + ' rson=' + t[rs(1)]) # 输出 A:lson=B rson=C
print(t[5] + ':lson=' + t[ls(5)] + ' rson=' + t[rs(5)]) # 输出 E:lson=J rson=K
其实,即使二叉树不是完全二叉树,而是普通二叉树,也可以用这种简单方法来存储。如果某个节点没有值,那就空着这个节点不用,方法是把它赋值为一个不该出现的值,例如赋值为0或无穷大INF。这样会浪费一些空间,好处是编程非常简单。
3 例题
二叉树是很基本的数据结构,大量算法、高级数据结构都是基于二叉树的。二叉树有很多操作,最基础的操作是搜索(遍历)二叉树的每个节点,有先序遍历、中序遍历、后序遍历。这3种遍历都用到了递归函数,二叉树的形态天然适合用递归来编程。
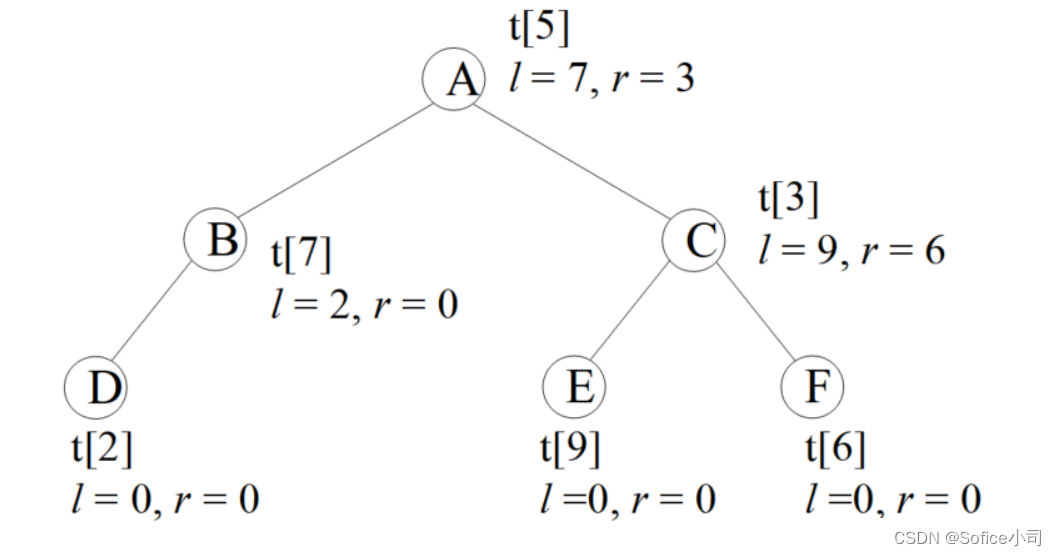
(1)先(父)序遍历,父节点在最前面输出。先输出父节点,再访问左孩子,最后访问右孩子。上图的先序遍历结果是ABDCEF。为什么?把结果分解为:A-BD-CEF。父亲是A,然后是左孩子B和它带领的子树BD,最后是右孩子C和它带领的子树CEF。这是一个递归的过程,每个子树也满足先序遍历,例如CEF,父亲是C,然后是左孩子E,最后是右孩子F。
(2)中(父)序遍历,父节点在中间输出。先访问左孩子,然后输出父节点,最后访问右孩子。上图的中序遍历结果是DBAECF。为什么?把结果分解为:DB-A-ECF。DB是左子树,然后是父亲A,最后是右子树ECF。每个子树也满足中序遍历,例如ECF,先左孩子E,然后是父亲C,最后是右孩子F。
(3)后(父)序遍历,父节点在最后输出。先访问左孩子,然后访问右孩子,最后输出父节点。上图的后序遍历结果是DBEFCA。为什么?把结果分解为:DB-EFC-A。DB是左子树,然后是右子树EFC,最后是父亲A。每个子树也满足后序遍历,例如EFC,先左孩子E,然后是右孩子F,最后是父亲C。
这三种遍历,中序遍历是最有用的,它是二叉查找树的核心。
例题 二叉树的遍历
(1)C++代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100005;
struct Node{int v; int ls, rs;
}t[N]; //tree[0]不用,0表示空结点
void preorder (int p){ //求先序序列if(p != 0){cout << t[p].v <<" "; //先序输出preorder (t[p].ls);preorder (t[p].rs);}
}
void midorder (int p){ //求中序序列if(p != 0){midorder (t[p].ls);cout << t[p].v <<" "; //中序输出midorder (t[p].rs);}
}
void postorder (int p){ //求后序序列if(p != 0){postorder (t[p].ls);postorder (t[p].rs);cout << t[p].v <<" "; //后序输出}
}
int main() {int n; cin >> n;for (int i = 1; i <= n; i++) {int a, b; cin >> a >> b;t[i].v = i;t[i].ls = a;t[i].rs = b;}preorder(1); cout << endl;midorder(1); cout << endl;postorder(1); cout << endl;
}
(2)Java代码
下面的Java代码和上面的C++代码略有不同。例如在preorder()中没有直接打印节点的值,而是用joiner.add()先记录下来,遍历结束后一起打印,这样快一些。本题 n = 1 0 6 n=10^6 n=106 ,规模大,时间紧张。
import java.util.Scanner;
import java.util.StringJoiner;
class Main {static class Node {int v, ls, rs;Node(int v, int ls, int rs) {this.v = v;this.ls = ls;this.rs = rs;}}static final int N = 100005;static Node[] t = new Node[N]; //tree[0]不用,0表示空结点static void preorder(int p, StringJoiner joiner) { //求先序序列if (p != 0) {joiner.add(t[p].v + ""); //不是直接打印,而是先记录下来preorder(t[p].ls,joiner);preorder(t[p].rs,joiner);}}static void midorder(int p, StringJoiner joiner) { //求中序序列if (p != 0) {midorder(t[p].ls,joiner);joiner.add(t[p].v + "");//中序输出midorder(t[p].rs,joiner);}}static void postorder(int p, StringJoiner joiner) { //求后序序列if (p != 0) {postorder(t[p].ls,joiner);postorder(t[p].rs,joiner);joiner.add(t[p].v + ""); //后序输出}}public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();for (int i = 1; i <= n; i++) {int a = sc.nextInt(), b = sc.nextInt();t[i] = new Node(i, a, b);}StringJoiner joiner = new StringJoiner(" "); preorder(1, joiner); System.out.println(joiner); joiner = new StringJoiner(" ");midorder(1, joiner); System.out.println(joiner);joiner = new StringJoiner(" ");postorder(1, joiner); System.out.println(joiner);}
}
(3)Python代码
N = 100005
t = [0] * N # tree[0]不用,0表示空结点
class Node:def __init__(self, v, ls, rs):self.v = vself.ls = lsself.rs = rsdef preorder(p): # 求先序序列if p != 0:print(t[p].v, end=' ') # 先序输出preorder(t[p].ls)preorder(t[p].rs)def midorder(p): # 求中序序列if p != 0:midorder(t[p].ls)print(t[p].v, end=' ') # 中序输出midorder(t[p].rs)def postorder(p): # 求后序序列if p != 0:postorder(t[p].ls)postorder(t[p].rs)print(t[p].v, end=' ') # 后序输出n = int(input())
for i in range(1, n+1):a, b = map(int, input().split())t[i] = Node(i, a, b)preorder(1); print()
midorder(1); print()
postorder(1); print()
4 习题
完全二叉树的权值
FBI树
American Heritage
求先序排列
相关文章:

【蓝桥杯软件赛 零基础备赛20周】第7周——二叉树
文章目录 1 二叉树概念2 二叉树的存储和编码2.1 二叉树的存储方法2.2 二叉树存储的编码实现2.3 二叉树的极简存储方法 3 例题4 习题 前面介绍的数据结构数组、队列、栈,都是线性的,它们存储数据的方式是把相同类型的数据按顺序一个接一个串在一起。简单的…...
SpringBoot+SSM项目实战 苍穹外卖(12) Apache POI
继续上一节的内容,本节是苍穹外卖后端开发的最后一节,本节学习Apache POI,完成工作台、数据导出功能。 目录 工作台Apache POI入门案例 导出运营数据Excel报表 工作台 工作台是系统运营的数据看板,并提供快捷操作入口,…...
Maven 基础总结篇
Maven 基础总结篇 Maven是专门用于管理和构建Java项目的工具,它的主要功能有: 提供了一套标准化的项目结构:用于解决不同IDE(例如eclipse与IDEA)不同的项目结构的问题 提供了一套标准化的构建流程(编译&…...

MySQL的导入导出及备份
一.准备导入之前 二.navicat导入导出 编辑 三.MySQLdump命令导入导出 四.load data file命令的导入导出 五.远程备份 六. 思维导图 一.准备导入之前 需要注意: 在导出和导入之前,确保你有足够的权限。在进行导入操作之前,确保目标数据…...
【机器学习】常见算法详解第2篇:K近邻算法各种距离度量(已分享,附代码)
本系列文章md笔记(已分享)主要讨论机器学习算法相关知识。机器学习算法文章笔记以算法、案例为驱动的学习,伴随浅显易懂的数学知识,让大家掌握机器学习常见算法原理,应用Scikit-learn实现机器学习算法的应用࿰…...

@KafkaListener指定kafka集群
基于KafkaListener注解的kafka监听代码可以手动指定要消费的kafka集群,这对于需要访问多套kafka集群的程序来说,是有效的解决方案。这里需要注意的是,此时的消费者配置信息需使用原生kafka的配置信息格式(如:ConsumerC…...

什么是算法的空间复杂度?
一、问题 常常⽤算法的空间复杂度来评价算法的性能,那么什么是算法的空间复杂度呢? 二、解答 算法的空间复杂度是指在算法的执⾏过程中,需要的辅助空间数量。 辅助空间数量指的不是程序指令、常数、指针等所需要的存储空间,也不是…...
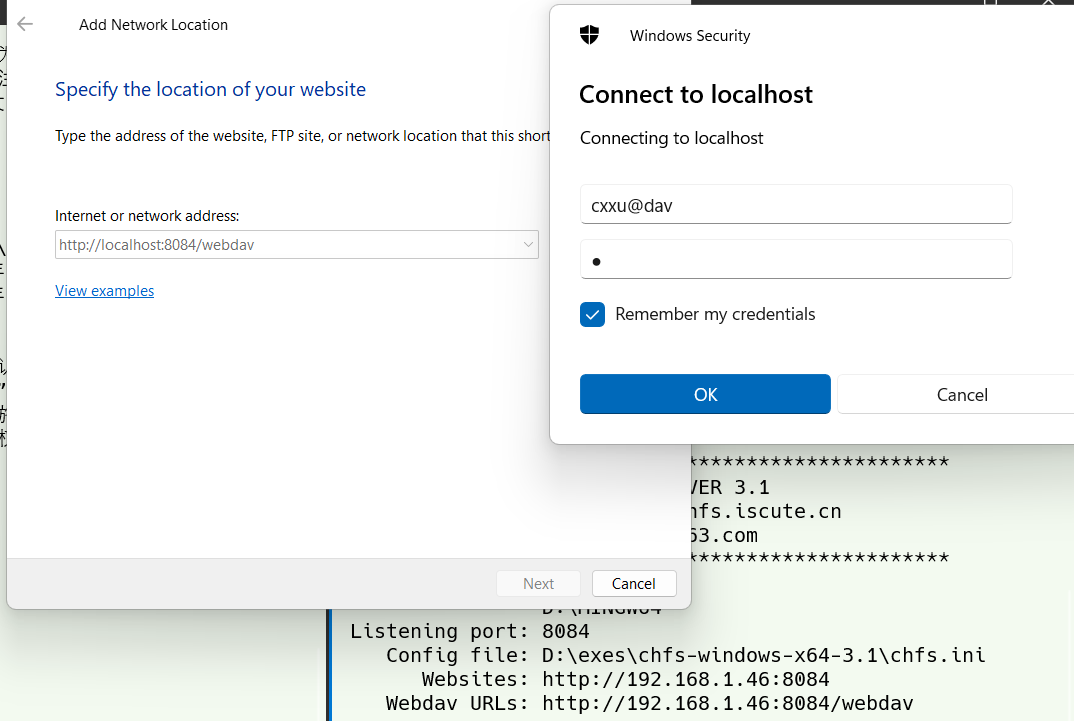
WebDav协议相关软件@简单配置局域网内的http和WebDav服务器和传输系统
文章目录 相关软件windows自带第三方软件 chfs(CuteHttpFileServer)下载软件GUI方案 补充命令行方案命令行程序定位简单创建服务站点使用配置文件配置细节 使用软连接或符号链接等手段将向共享站点的根目录添加文件开机自启服务包装nssm包装使用powershell包装 服务启动chfs服务…...

自定义数据实现SA3D
SA3D:Segment Anything in 3D with NeRFs 实现了3D目标分割 原理是利用SAM(segment anything) 模型和Nerf分割渲染3D目标, SAM只能分块,是没有语义标签的,如何做到语义连续? SA3D中用了self-prompt, 根据前一帧的mask…...

设计模式基础概念:探索设计模式的魅力
设计模式是软件开发中的一种指导性概念,它提供了一套被广泛接受的解决方案,用于常见的设计问题。设计模式有助于提高软件的可重用性、可扩展性和可维护性,并促进团队之间的沟通。 以下是一些常见的设计模式: 创建型模式࿱…...

【Leetcode】2182. 构造限制重复的字符串
文章目录 题目思路代码 题目 2182. 构造限制重复的字符串 问题:给你一个字符串 s 和一个整数 repeatLimit ,用 s 中的字符构造一个新字符串 repeatLimitedString ,使任何字母 连续 出现的次数都不超过 repeatLimit 次。你不必使用 s 中的全…...
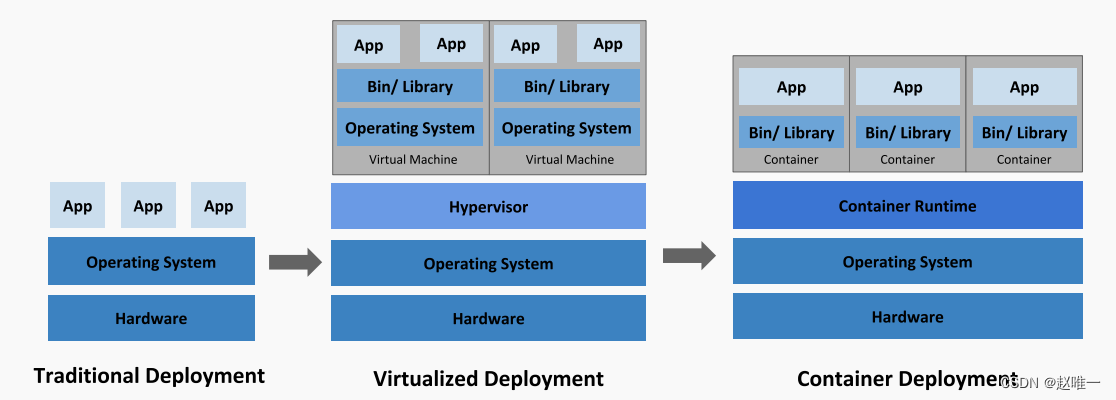
Kubernetes(K8S)云服务器实操TKE
一、 Kubernetes(K8S)简介 Kubernetes源于希腊语,意为舵手,因为首尾字母中间正好有8个字母,简称为K8S。Kubernetes是当今最流行的开源容器管理平台,是 Google 发起并维护的基于 Docker 的开源容器集群管理系统。它是大名鼎鼎的Google Borg的开源版本。 K8s构建在 Docker …...

设置弹窗随鼠标位置移动
1.这是要移动的弹窗,隐藏显示逻辑、样式、展示内容自己写,主要就是动态设置弹窗的style,floatLeft和floatTop都是Vue中的data双向绑定数据; <div id"box" v-show"hasMove" :style"{ left: floatLeft…...

Spring Boot实现数据加密脱敏:注解 + 反射 + AOP
文章目录 1. 引言2. 数据加密和脱敏的需求3. Spring Boot项目初始化4. 敏感数据加密注解设计5. 实现加密和脱敏的工具类6. 实体类和加密脱敏注解的使用7. 利用AOP实现加密和脱敏8. 完善AOP切面9. 测试10. 拓展功能与未来展望10.1 加密算法的选择10.2 动态注解配置 11. 总结 &am…...
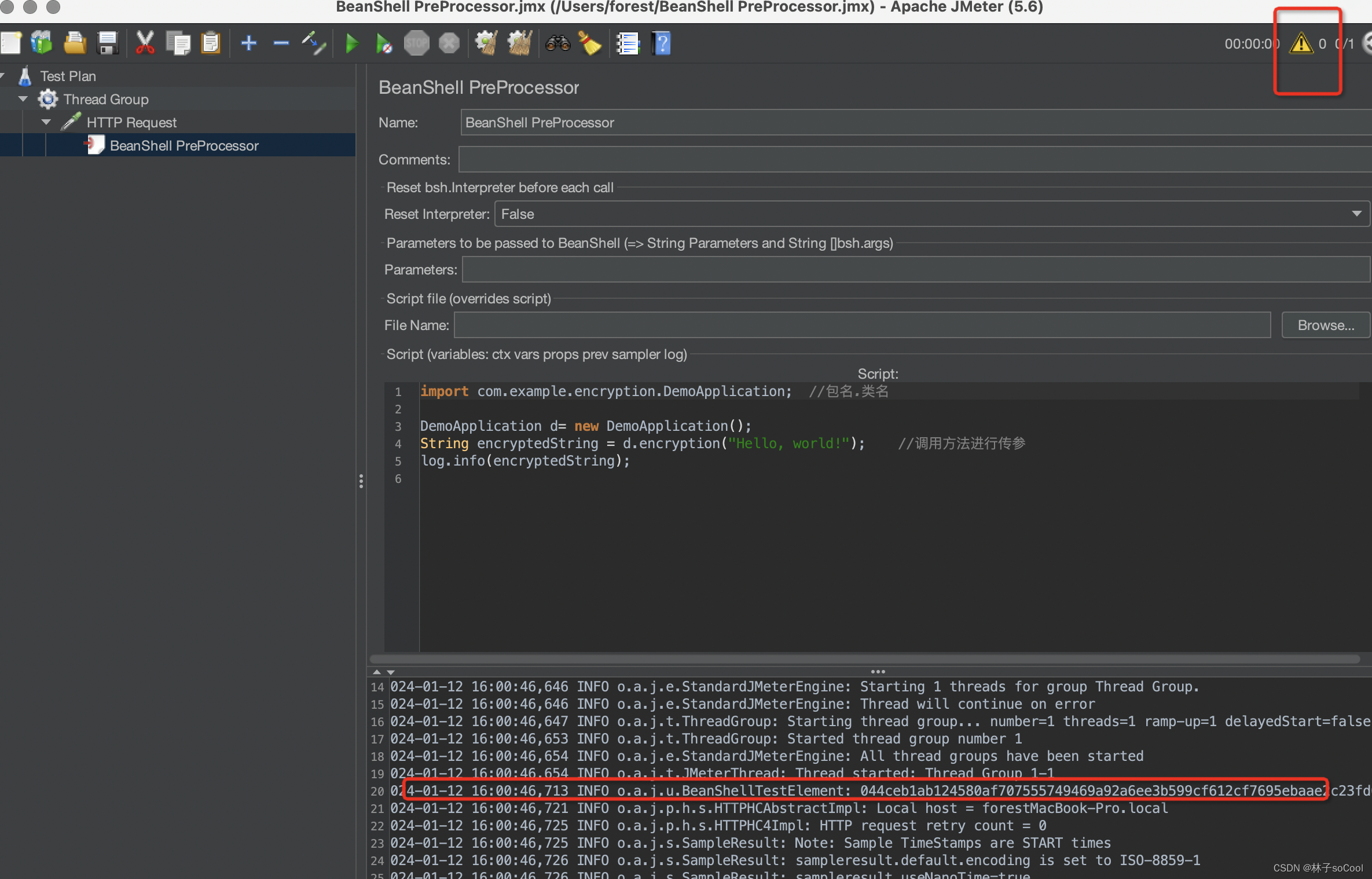
jmeter和meterSphere如何使用第三方jar包
工具引用jar包语言都是beanshell 问题起因:metersphere 接口自动化实现过程中,如何实现字符串加密且加密方法依赖第三方库; 使用语言:beanshell脚本语言,java语言 使用工具:idea jmeter metersphere 1.首…...
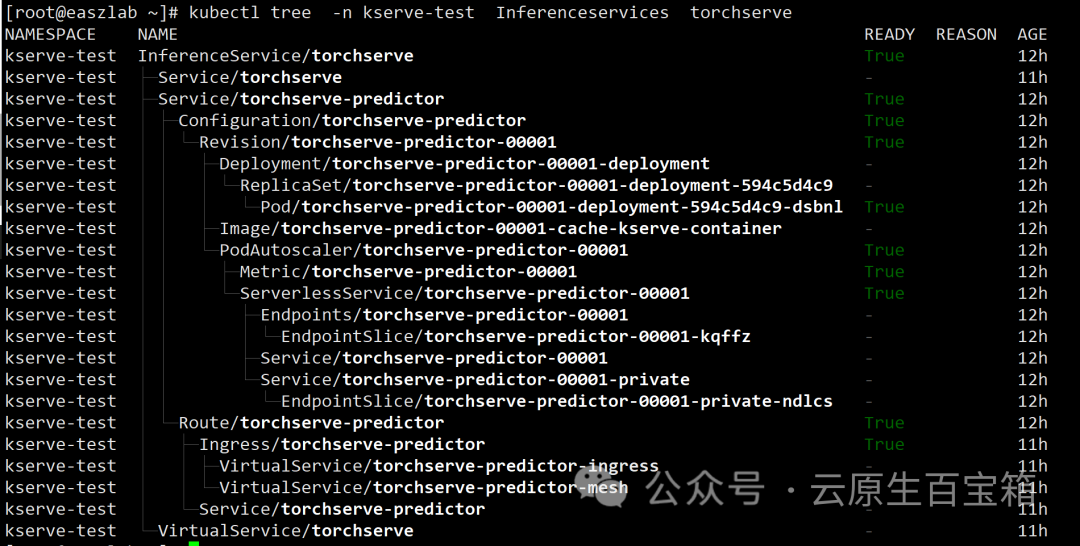
API对象上千个,有啥关联性,kubectl-tree一键搞定
关注【云原生百宝箱】公众号,获取更多云原生消息 "kubectl-tree 是一款强大的 kubectl 插件,通过 ownerReferences 实现 Kubernetes 对象之间的所有权关系探索。相较于 kubectl lineage,它不仅更全面理解 API 对象的逻辑关系,…...

java自定义工具类在List快速查找相同字段值对象
根据对象某一字段名,获取字段值,将List转换为Map中包含list,Key为字段值,Value为相同字段值的对象list,快速定位具有相同字段值的对象,转换之后便于在Map中根据字段值快速查找相同字段值的对象 //List转Map…...

codeforces Hello 2024 - C - Grouping Increases --- 题解
目录 Grouping Increases 题目描述: 思路解析: 代码实现: Grouping Increases 题目描述: 给你一个大小为n的数组a,你可以把数组a划分为两个子序列s和t,a中元素,要么在子序列s中,…...
STM32H5培训(一)总览
文章目录 1. 前言2. STM32H5系列MCU的特点和新功能包括性能提升、新外设和安全功能等3. STM32H5系列型号之间的区别和关键资源对比4. 性能和功能亮点6. 开发生态参考: 1. 前言 本篇主要介绍STM32H5系列MCU的特点和新功能,包括全新的M33内核、250M主频处…...

亚马逊云科技 WAF 部署小指南(五):在客户端集成 Amazon WAF SDK 抵御 DDoS 攻击...
方案介绍 在 WAF 部署小指南(一)中,我们了解了 Amazon WAF 的原理,并通过创建 WEB ACL 和托管规则防护常见的攻击。也了解了通过创建自定义规则在 HTTP 请求到达应用之前判断是阻断还是允许该请求。在 Amazon WAF 自定义规则中&am…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
