KY43 全排列
全排列板子
ti
#include<bits/stdc++.h>using namespace std;string s;
map<string, int>mp;void swap(char &a, char &b){char em = a;a = b;b = em;
}void dfs(int n){ //将s[n~l]的全排列转化成s[n]s[n+1~l]的全排列 if(n == s.length()){mp[s] = 1;return ;}for(int i = n; i < s.length(); i ++ ){swap(s[n], s[i]); //for和这个swap一起保证第n位所有字母都有可能 dfs(n + 1); //进到这一步,第n位的字母都定了, swap(s[n], s[i]);}
}int main()
{cin>>s;dfs(0);for(auto i = mp.begin(); i != mp.end(); i ++ ){cout<<i->first<<endl;}return 0;
}
第二种解法
next_permutation,自带的全排列库函数,但是他只会按照输入的s的顺序排列,所以要先sort一下
#include<bits/stdc++.h>using namespace std;string s;int main()
{cin>>s;sort(s.begin(), s.end());cout<<s<<endl;for(s.begin(); next_permutation(s.begin(), s.end());){cout<<s<<endl;}return 0;
}
相关文章:

KY43 全排列
全排列板子 ti #include<bits/stdc.h>using namespace std;string s; map<string, int>mp;void swap(char &a, char &b){char em a;a b;b em; }void dfs(int n){ //将s[n~l]的全排列转化成s[n]s[n1~l]的全排列 if(n s.length()){mp[s] 1;return ;}f…...
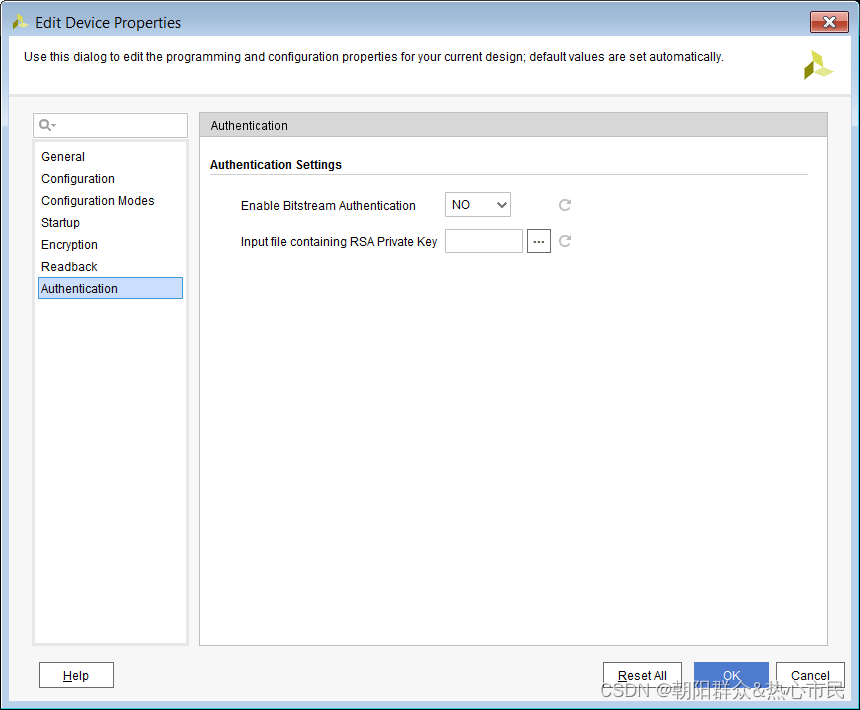
UltraScale 和 UltraScale+ 生成已加密文件和已经过身份验证的文件
注释 :如需了解更多信息,请参阅《使用加密和身份验证确保 UltraScale/UltraScale FPGA 比特流的安全》 (XAPP1267)。 要生成加密比特流,请在 Vivado IDE 中打开已实现的设计。在主工具栏中,依次选择“Flow” → “Bitstream Setti…...

2023年全国职业院校技能大赛软件测试赛题—单元测试卷②
单元测试 一、任务要求 题目1:任意输入2个正整数值分别存入x、y中,据此完成下述分析:若x≤0或y≤0,则提示:“输入不符合要求。”;若2值相同,则提示“可以构建圆形或正方形”;若2<…...
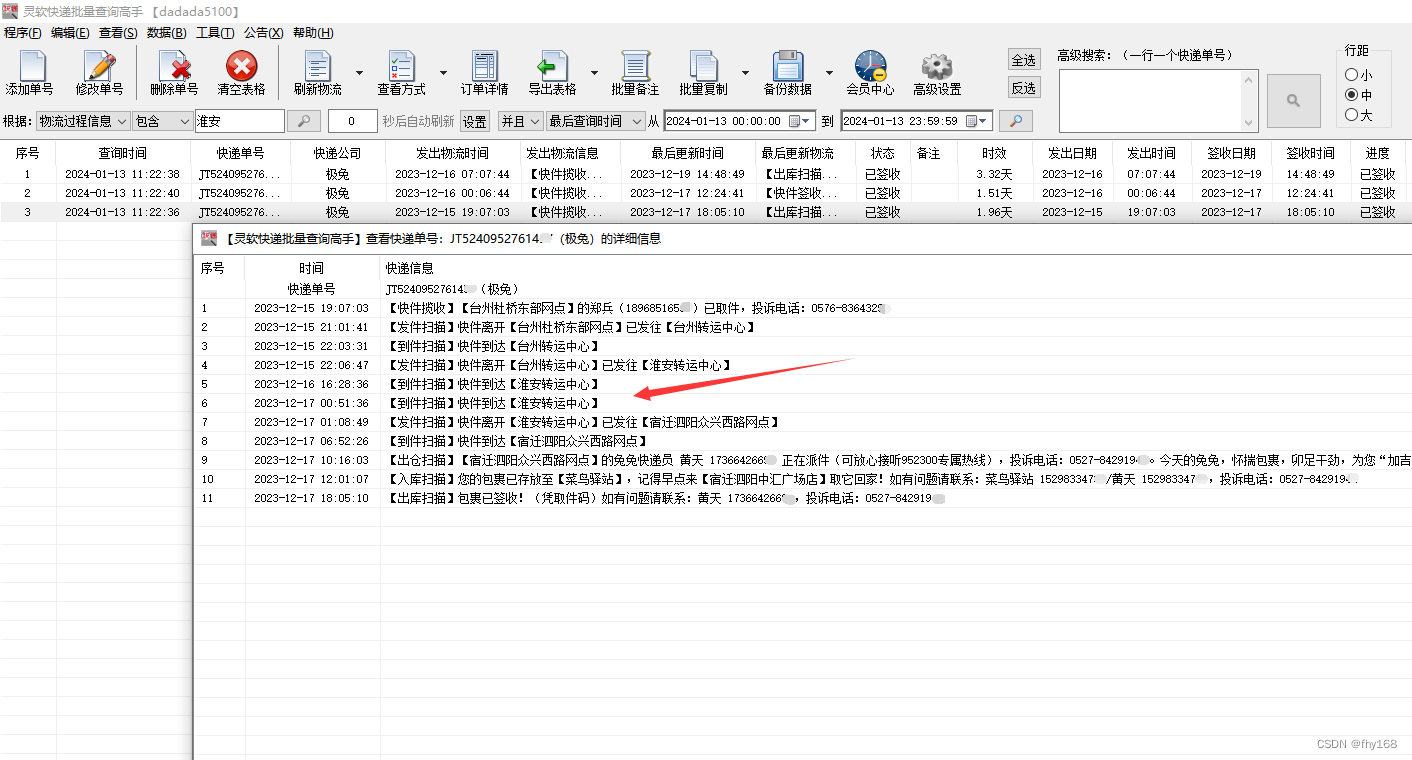
极兔单号查快递,极兔快递单号查询,筛选出途经指定城市的单号
随着电商的繁荣,快递单号已经成为我们生活中的一部分。然而,面对海量的快递信息,如何快速、准确地筛选出我们需要的单号,变成了许多人的痛点。今天,我要为你介绍一款强大的工具——快递批量查询高手,让你的…...

[redis] redis高可用之持久化
一、Redis 高可用的相关知识 1.1 什么是高可用 在web服务器中,高可用是指服务器可以正常访问的时间,衡量的标准是在多长时间内可以提供正常服务(99.9%、99.99%、99.999%等等)。 但是在Redis语境中,高可用的含义似乎要宽泛一些,…...
)
云原生 微服务 restapi devops相关的一些概念说明(持续更新中)
云原生: 定义 云原生是一种构建和运行应用程序的方法,是一套技术体系和方法论。它是一种在云计算环境中构建、部署和管理现代应用程序的软件方法。云原生应用程序是基于微服务架构的,采用开源堆栈(K8SDocker)进行容器…...
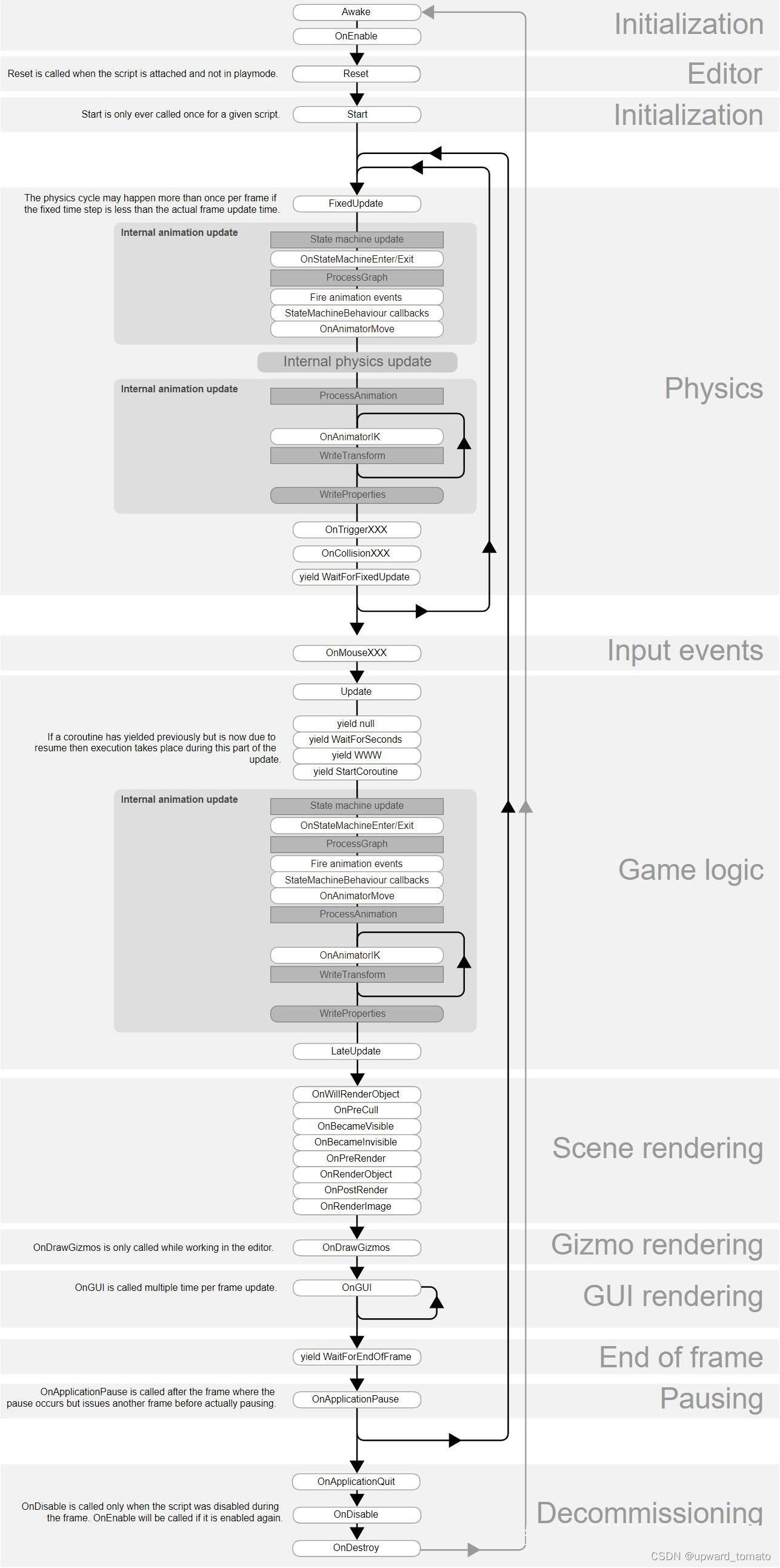
初学unity学习七天,经验收获总结
初学unity七天,经验收获总结 学习就是认识新观念和新想法的过程。 假如人们始终以同一种思维方式来考虑问题的话,那么始终只会得到同样的结果。 因为我对你讲述的许多内容是你以前从未接触过的,所以我建议你,在你还没有做之前&…...

hcip实验2
根据地址分配完成基础配置 先配置r1,r2,r3的ospf以及与isp通讯: 配置缺省路由: 完成nat配置: 完成r5,r6,r7,r8,r15的mgre以及整个网络的ospf配置 mgre: area 2 和3之间用多进程双向重发布技术完成: area4和5之间用虚…...
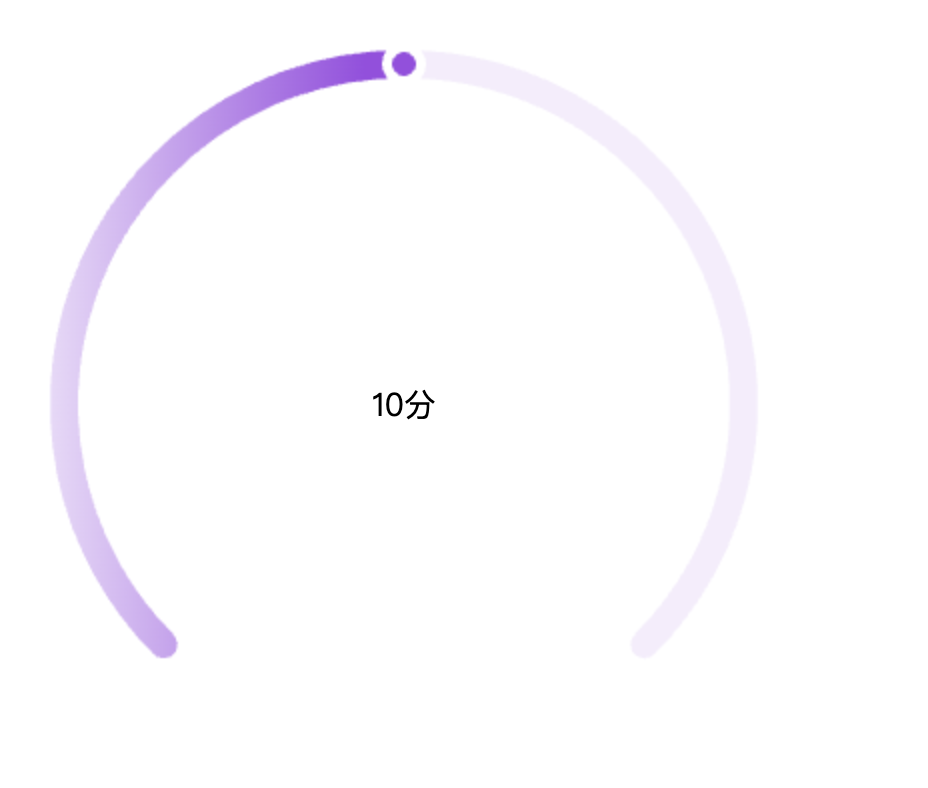
js:使用canvas画一个半圆
背景 需求需要画一个半圆,或者多半圆,其实一下子就能想到 canvas 中的圆弧,核心使用 context.arc context.arc(x,y,r,sAngle,eAngle,counterclockwise)接下来我们看看示例 例一 <!DOCTYPE html> <html lang"en"> &…...
1.框架介绍项目环境配置与项目启动!
目录 1.框架开发方向:2.项目启动与环境搭建 1.框架开发方向: 1.前后端分离项目 2.纯后端项目 3.移动端开发uni-app(ios、Android、H5、微信小程序) 4.内容管理系统2.项目启动与环境搭建 1.安装node.js 下载地址可以用nvm安装 便于运行前端项目https://juejin.cn/post/7094576…...

LeetCode算法题解:螺旋矩阵
LeetCode算法题解:螺旋矩阵 题目描述 给定一个 m x n 的矩阵,按照螺旋顺序返回矩阵中的所有元素。 解题思路 1. 初始化变量 我们首先定义四个边界变量来跟踪螺旋遍历的边界:top、bottom、left 和 right。 2. 螺旋遍历 开始从左到右遍历…...

【Java 设计模式】设计原则之开放封闭原则
文章目录 1. 定义2. 好处3. 应用4. 示例结语 在软件开发中,设计原则是创建灵活、可维护和可扩展软件的基础。 这些原则为我们提供了指导方针,帮助我们构建高质量、易理解的代码。 ✨单一职责原则(SRP) ✨开放/封闭原则(…...

数据分析求职-知识脑图
今天和大家聊聊数据分析求职常见面试题,这是这个系列的第一篇文章,但是我不想开始就直接罗列题目,因为这样的文章实在太多了,同学们的兴趣程度肯定一般。所以,我想先和大家聊聊在准备面试题时候通常遇到的困扰…...

SQL-修改数据
🎉欢迎您来到我的MySQL基础复习专栏 ☆* o(≧▽≦)o *☆哈喽~我是小小恶斯法克🍹 ✨博客主页:小小恶斯法克的博客 🎈该系列文章专栏:重拾MySQL 🍹文章作者技术和水平很有限,如果文中出现错误&am…...

Rockchip | FIQ-Debugger调试工具
FIQ-Debugger fiq debugger是集成到内核中的一种系统调试手段。 FIQ在arm架构中相当于nmi中断,fiq debugger把串口注册成fiq中断,在串口fiq中断服务程序中集成了一些系统调试命令。 一般情况下串口是普通的console模式,在串口工具下键盘输入…...

第二百六十三回 给geolocator插件提交问题
文章目录 1. 知识回顾2. 问题描述与解决2.1 问题描述2.2 问题解决 3. 心得与感受 1. 知识回顾 我们在前面章回中介绍过如何获取位置信息,主要介绍的是geolocator这个三方包,不过在最近使用时却发现了问题,尝试搜索解决,但是没有结…...

分组背包问题
题目来源:9. 分组背包问题 - AcWing题库 题目: 有 N 组物品和一个容量是 V 的背包。 每组物品有若干个,同一组内的物品最多只能选一个。 每件物品的体积是 vij,价值是 wij,其中 i 是组号,j 是组内编号。 …...

WinForm 中Label自动换行 解决方法
Label自动换行 1.单行完全显示:Label.AutoSize true; 2.换行显示:Label. AutoSize false;(Label框高度用户指定)。 3.多行显示 根据字数自动控制高度:Label.AutoSize true;Label.MaximumSize new Size(w,0); …...
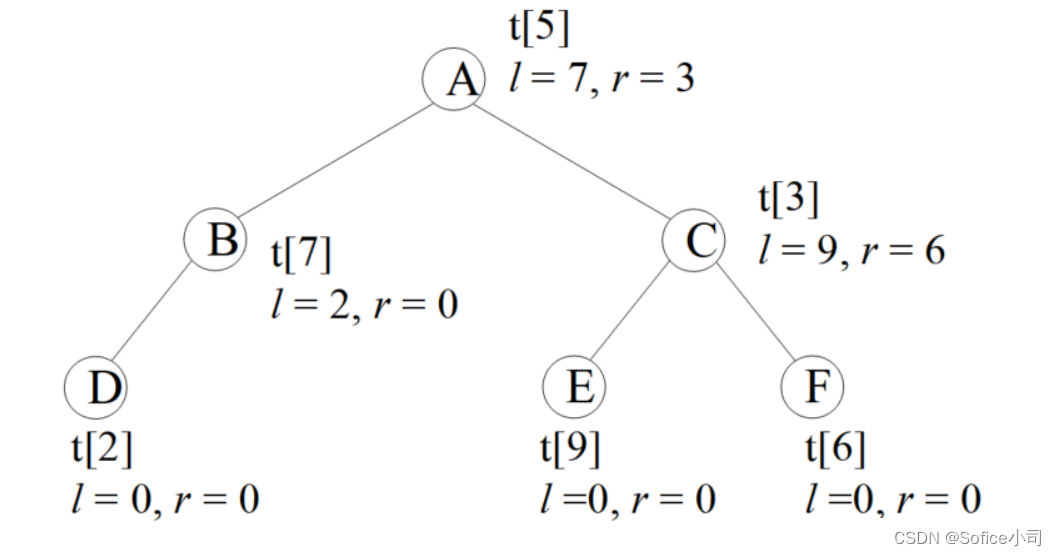
【蓝桥杯软件赛 零基础备赛20周】第7周——二叉树
文章目录 1 二叉树概念2 二叉树的存储和编码2.1 二叉树的存储方法2.2 二叉树存储的编码实现2.3 二叉树的极简存储方法 3 例题4 习题 前面介绍的数据结构数组、队列、栈,都是线性的,它们存储数据的方式是把相同类型的数据按顺序一个接一个串在一起。简单的…...
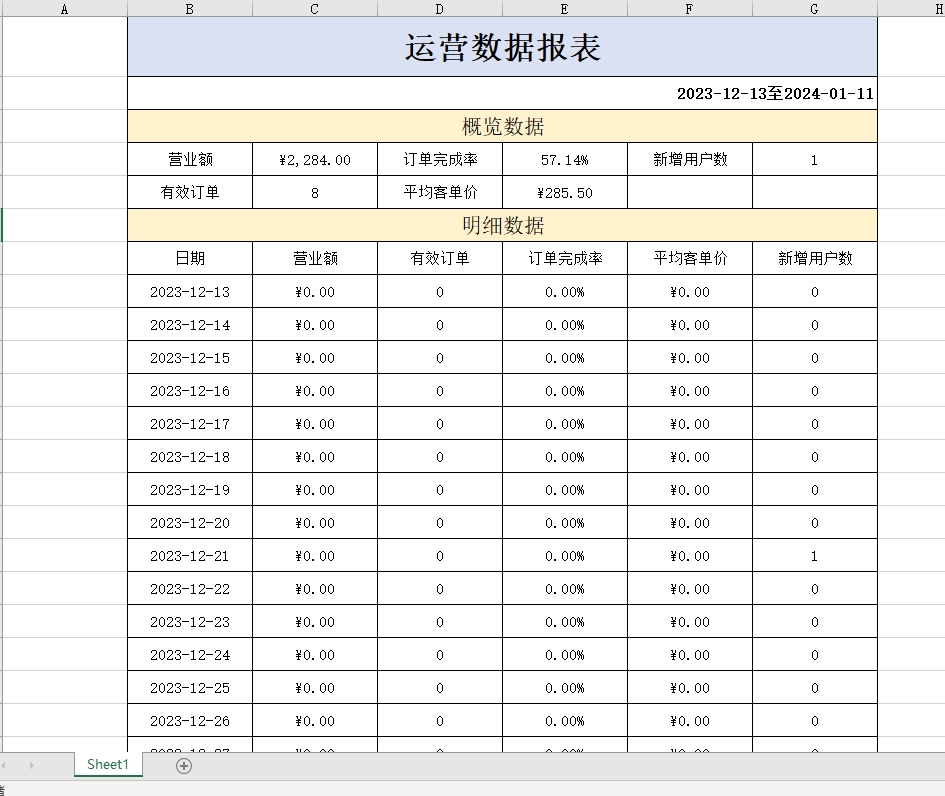
SpringBoot+SSM项目实战 苍穹外卖(12) Apache POI
继续上一节的内容,本节是苍穹外卖后端开发的最后一节,本节学习Apache POI,完成工作台、数据导出功能。 目录 工作台Apache POI入门案例 导出运营数据Excel报表 工作台 工作台是系统运营的数据看板,并提供快捷操作入口,…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...
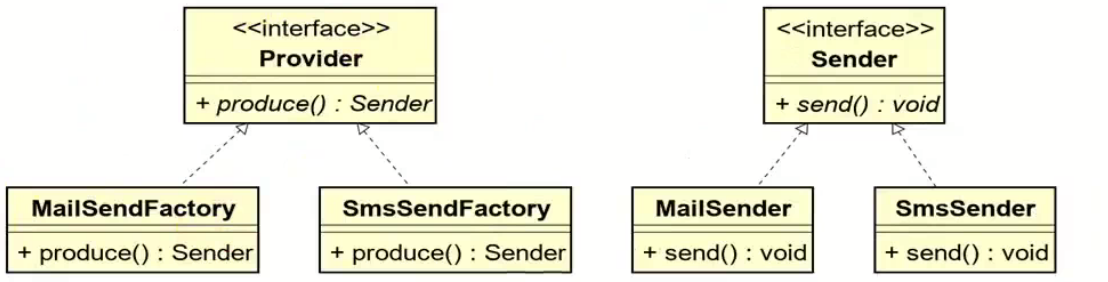
工厂方法模式和抽象工厂方法模式的battle
1.案例直接上手 在这个案例里面,我们会实现这个普通的工厂方法,并且对比这个普通工厂方法和我们直接创建对象的差别在哪里,为什么需要一个工厂: 下面的这个是我们的这个案例里面涉及到的接口和对应的实现类: 两个发…...
