池化、线性、激活函数层
一、池化层
池化运算是深度学习中常用的一种操作,它可以对输入的特征图进行降采样,从而减少特征图的尺寸和参数数量。
池化运算的主要目的是通过“收集”和“总结”输入特征图的信息来提取出主要特征,并且减少对细节的敏感性。在池化运算中,通常有两种常见的操作:最大池化和平均池化。
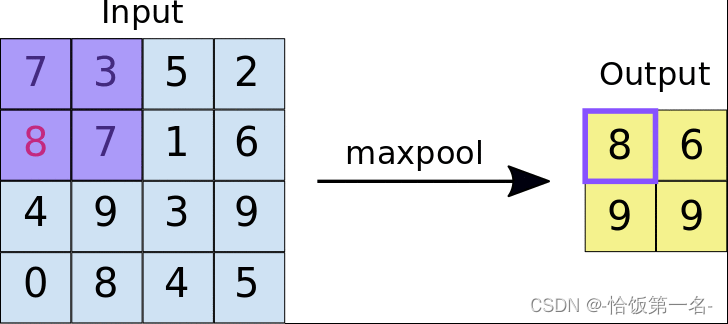

最大池化(Max Pooling)是指在池化窗口内选择最大值作为输出的操作。它可以帮助提取输入特征图中的最显著特征,同时减少了特征图的尺寸。
平均池化(Average Pooling)是指在池化窗口内计算平均值作为输出的操作。它可以对输入特征图进行平滑处理,减少噪声和细节的影响
池化运算通常应用于卷积神经网络的后续层,可以有效地减少特征图的维度,并且具有一定的平移不变性,即对输入的微小平移具有一定的鲁棒性。
总结起来,池化运算通过“收集”输入特征图的信息并进行“总结”,帮助提取主要特征并减少特征图的尺寸。最大池化和平均池化是常见的池化操作,分别选择最大值和平均值作为输出。这些操作在深度学习中被广泛应用于图像识别和计算机视觉任务中。
nn.MaxPool2d
nn.MaxPool2d是PyTorch中用于对二维信号(如图像)进行最大值池化的类。它可以通过选择池化窗口内的最大值来减少特征图的尺寸。
nn.MaxPool2d的主要参数如下:
kernel_size:池化核尺寸,指定池化窗口的大小。stride:步长,指定池化窗口在输入特征图上滑动的步长。默认值为None,表示使用与kernel_size相同的值。padding:填充个数,指定在输入特征图周围添加的填充像素数。默认值为0。dilation:池化核间隔大小,指定池化核中的元素之间的间距。默认值为1。return_indices:是否记录池化像素的索引。如果设置为True,则在池化操作中会返回一个张量,其中包含池化像素的索引。默认值为False。ceil_mode:是否向上取整。如果设置为True,则在计算输出特征图的尺寸时会向上取整。默认值为False。
nn.AvgPool2d
nn.AvgPool2d是PyTorch中的一个二维平均池化层,用于对二维信号(如图像)进行平均值池化操作。下面是对主要参数的详细解释:
- kernel_size(池化核尺寸):
- 可以是一个整数,表示池化核的高度和宽度相等。
- 也可以是一个元组(kH,kW),分别表示池化核的高度和宽度。
- stride(步长):
- 可以是一个整数,表示在高度和宽度上的步长相等。
- 也可以是一个元组(sH,sW),分别表示在高度和宽度上的步长。
- padding(填充个数):
- 可以是一个整数,表示在输入的每一条边周围填充0的个数。
- 也可以是一个元组(padH,padW),分别表示在输入的高度和宽度上填充0的个数。
- ceil_mode(尺寸向上取整):
- 一个布尔值,表示是否向上取整输出的尺寸。
- 如果为False(默认值),则向下取整。
- 如果为True,则向上取整。
- count_include_pad(填充值用于计算):
- 一个布尔值,表示在计算平均值时是否包括填充值。
- 如果为True(默认值),则包括填充值。
- 如果为False,则不包括填充值。
- divisor_override(除法因子):
- 一个整数,用于覆盖默认的除法因子。
- 如果设置了该参数,则用它来除以池化窗口的总元素数。
nn.AvgPool2d(kernel_size, stride=None, padding=0, ceil_mode=False, count_include_pad=True, divisor_override=None)
这些参数可以根据需要进行调整,以控制池化操作的行为。
nn.MaxUnpool2d
对二维信号(图像)进行最大值池化和上采样是常用的图像处理操作。在PyTorch中,可以使用nn.MaxPool2d进行最大值池化操作,使用nn.MaxUnpool2d进行上采样操作。下面是对主要参数的详细解释:
- nn.MaxPool2d(最大值池化):
- kernel_size(池化核尺寸):可以是一个整数或一个元组,表示池化核的高度和宽度。
- stride(步长):可以是一个整数或一个元组,表示在高度和宽度上的步长。
- padding(填充个数):可以是一个整数或一个元组,表示在输入的每一条边周围填充0的个数。
- nn.MaxUnpool2d(上采样):
- kernel_size(池化核尺寸):可以是一个整数或一个元组,表示池化核的高度和宽度。
- stride(步长):可以是一个整数或一个元组,表示在高度和宽度上的步长。
- padding(填充个数):可以是一个整数或一个元组,表示在输入的每一条边周围填充0的个数。
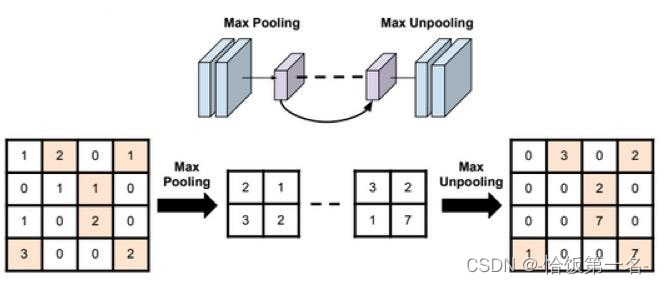
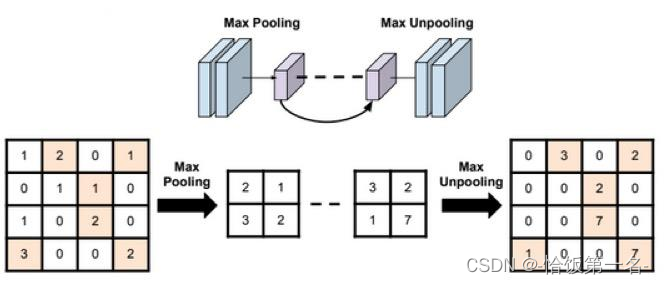
在进行上采样时,需要使用nn.MaxUnpool2d的forward方法,其中的参数包括: - input:输入张量,即经过最大值池化的特征图。
- indices:最大值池化过程中记录的最大值的索引,用于恢复原始特征图。
- output_size:输出的尺寸,可以是一个整数或一个元组,表示上采样后的特征图的尺寸。
使用nn.MaxPool2d对图像进行最大值池化,可以提取图像的主要特征。使用nn.MaxUnpool2d进行上采样,可以恢复池化之前的原始特征图尺寸。
线性层
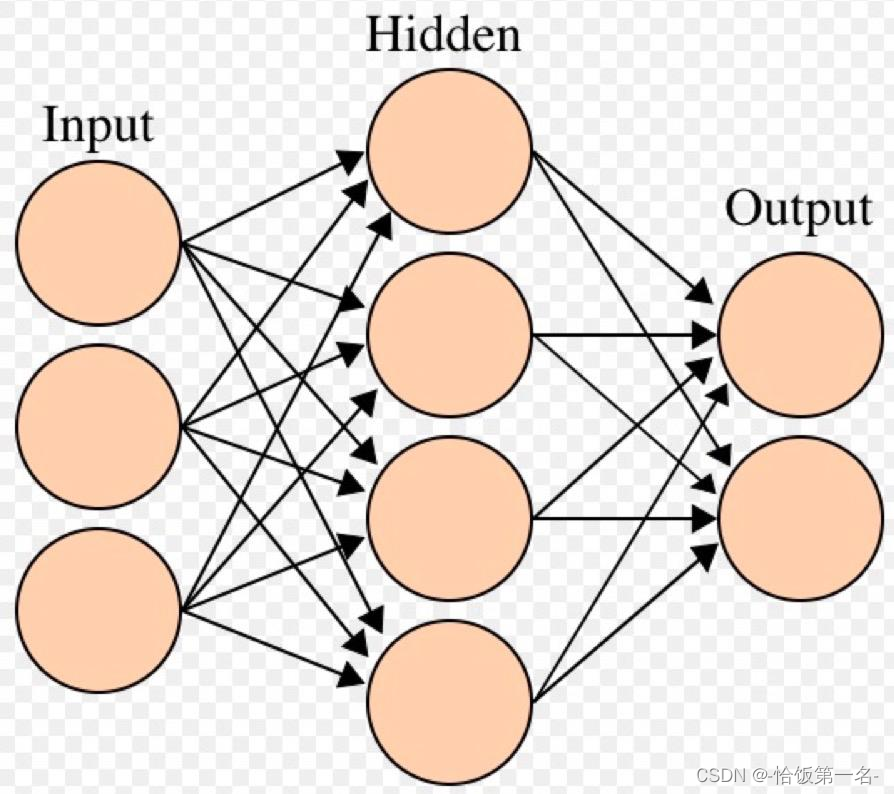
我们可以使用矩阵乘法来计算线性层的输出。下面是对计算步骤的详细解释:

- 输入数据(Input):
- 输入数据是一个形状为(1, 3)的张量,表示一组样本,每个样本有3个特征。
- 输入数据为[1, 2, 3],可以表示为一个1行3列的矩阵。
- 权重矩阵(W_0):
- 权重矩阵是一个形状为(3, 4)的张量,表示线性层中每个神经元与上一层所有神经元之间的连接权重。
- 权重矩阵为:
1 1 1 1
2 2 2 2
3 3 3 3 - 权重矩阵的行数等于输入数据的特征数,列数等于线性层的神经元数。
- 线性组合(Hidden):
- 线性组合可以通过矩阵乘法来实现。将输入数据(Input)与权重矩阵(W_0)相乘,得到线性组合的结果。
- 矩阵乘法的规则是,输入数据的每一行与权重矩阵的每一列对应元素相乘,然后将乘积相加。
- 根据计算,线性组合的结果为:
[11 + 21 + 31 + 41, 12 + 22 + 32 + 42, 13 + 23 + 33 + 43, 14 + 24 + 34 + 44]
= [6, 12, 18, 24]
因此,根据给定的输入数据和权重矩阵,线性层的输出为[6, 12, 18, 24]。
nn.Linear
nn.Linear是PyTorch中的线性层(全连接层)模块,用于对一维信号(向量)进行线性组合。下面是对主要参数的详细解释:
- in_features(输入结点数):
- 一个整数,表示输入向量的维度(结点数)。
- 输入向量的形状应为(batch_size, in_features)。
- out_features(输出结点数):
- 一个整数,表示输出向量的维度(结点数)。
- 输出向量的形状为(batch_size, out_features)。
- bias(是否需要偏置):
- 一个布尔值,表示是否在线性组合中使用偏置。
- 如果为True,则线性组合的计算公式为:y = 𝒙𝑾𝑻 + 𝒃𝒊𝒂。
- 如果为False,则线性组合的计算公式为:y = 𝒙𝑾𝑻。
在使用nn.Linear时,输入向量𝒙会与权重矩阵𝑾进行矩阵乘法运算,然后加上偏置𝒃(如果bias为True)。最终得到输出向量𝒚。
例如,如果输入向量𝒙的形状为(batch_size, in_features),权重矩阵𝑾的形状为(in_features, out_features),偏置𝒃的形状为(out_features,),则输出向量𝒚的形状为(batch_size, out_features)。
激活函数层
激活函数对特征进行非线性变换,赋予多层神经网络具有深度的意义
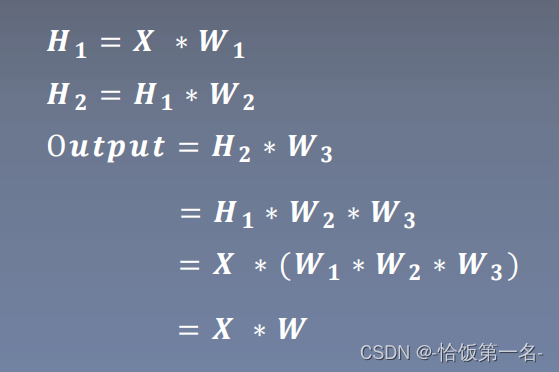
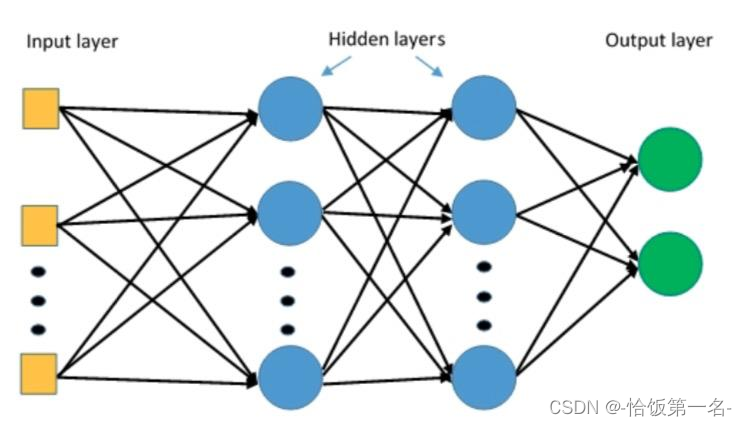
- 描述了一个多层神经网络的计算过程,其中𝑿表示输入特征,𝑾𝟏、𝑾𝟐、𝑾𝟑表示权重矩阵,𝑯𝟏、𝑯𝟐表示隐藏层的输出,O𝒖𝒕𝒑𝒖𝒕表示神经网络的输出。
- 在这个计算过程中,每一层的输出都是通过将输入特征与对应的权重矩阵相乘得到的。这种线性组合的过程只能对特征进行线性变换,无法处理非线性的关系。为了赋予神经网络更强的表达能力,需要引入激活函数对特征进行非线性变换。
- 激活函数的作用是将线性组合的结果进行非线性映射,从而引入非线性关系。常用的激活函数包括ReLU、Sigmoid、Tanh等。将激活函数应用于每一层的输出,可以增加神经网络的表达能力,使其能够学习更复杂的模式和关系。
- 根据提供的公式,可以将其表示为𝑿 ∗ 𝑾,其中𝑾表示整个多层神经网络的权重矩阵,包括𝑾𝟏、𝑾𝟐、𝑾𝟑。这个公式表达了多层神经网络对输入特征进行线性组合和非线性变换的过程。
nn.Sigmoid

nn.Sigmoid是PyTorch中的Sigmoid激活函数模块,用于对输入进行非线性变换。下面是对Sigmoid激活函数的特性的详细解释:

- 计算公式:
- Sigmoid激活函数的计算公式为:𝐲 = 1 / (1 + 𝒆^(-𝒙)),其中𝒙表示输入。
- Sigmoid函数将输入映射到一个取值范围在(0, 1)之间的输出。
- 梯度公式:
- Sigmoid函数的导数公式为:𝒚’ = 𝒚 * (1 - 𝒚),其中𝒚表示Sigmoid函数的输出。
- Sigmoid函数的导数范围在[0, 0.25]之间。
- 这意味着在反向传播过程中,梯度会逐渐减小,容易导致梯度消失的问题。
- 特性:
- 输出值在(0, 1)之间,符合概率的范围。
- Sigmoid函数的导数范围较小,容易导致梯度消失的问题,尤其在深层神经网络中。
- 输出为非0均值,这可能会破坏数据的分布特性,导致训练不稳定。
由于Sigmoid函数的导数范围较小,容易导致梯度消失的问题,在深层神经网络中,通常会选择其他的激活函数,如ReLU、LeakyReLU等,以解决梯度消失的问题。
nn.tanh
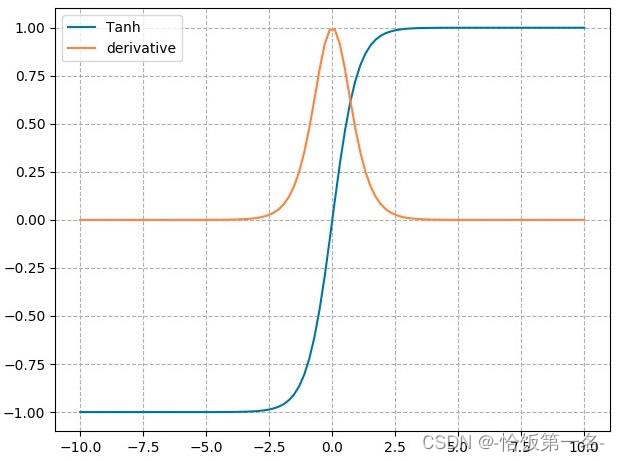

nn.tanh是PyTorch中的tanh激活函数模块,用于对输入进行非线性变换。下面是对tanh激活函数的特性的详细解释:
- 计算公式:
- tanh激活函数的计算公式为:𝐲 = (𝒆^𝒙 - 𝒆^(-𝒙)) / (𝒆^𝒙 + 𝒆^(-𝒙)),其中𝒙表示输入。
- tanh函数将输入映射到一个取值范围在(-1, 1)之间的输出。
- 梯度公式:
- tanh函数的导数公式为:𝒚’ = 1 - 𝒚^2,其中𝒚表示tanh函数的输出。
- tanh函数的导数范围在(0, 1)之间。
- 这意味着在反向传播过程中,梯度会逐渐减小,容易导致梯度消失的问题。
- 特性:
- 输出值在(-1, 1)之间,数据符合0均值的特性。
- tanh函数的导数范围较小,容易导致梯度消失的问题,尤其在深层神经网络中。
与Sigmoid函数类似,由于tanh函数的导数范围较小,容易导致梯度消失的问题,在深层神经网络中,通常会选择其他的激活函数,如ReLU、LeakyReLU等,以解决梯度消失的问题。
nn.ReLU

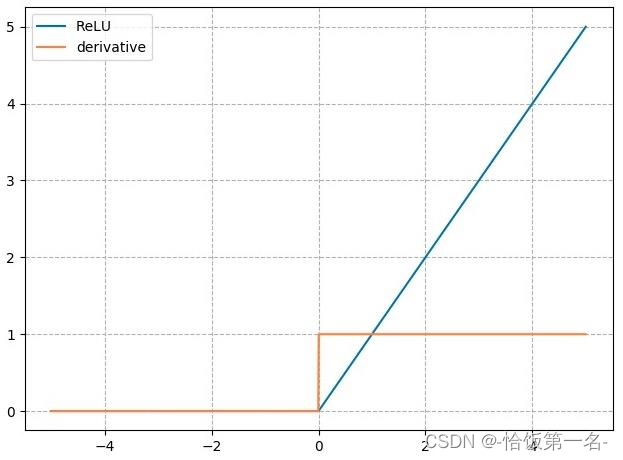
ReLU(Rectified Linear Unit)是一种常用的激活函数,它在深度学习中广泛应用。它的计算公式为𝑦 = max(0, 𝑥),其中𝑥是输入,𝑦是输出。
ReLU的梯度公式为:
𝑦’ = 1, 𝑥 > 0
𝑦’ = 0, 𝑥 ≤ 0
ReLU的特性如下:
- 输出值均为正数,负半轴导致死神经元:当输入𝑥大于0时,ReLU的输出为𝑥,保持正数;当输入𝑥小于等于0时,ReLU的输出为0,将负数归零。这种特性可以使神经网络更好地处理正数输入。
- 导数是1,缓解梯度消失,但易引发梯度爆炸:当输入𝑥大于0时,ReLU的导数为1,保持梯度不变,有助于缓解梯度消失问题;但当输入𝑥小于等于0时,ReLU的导数为0,梯度完全消失。这也意味着ReLU在反向传播过程中可能会遇到梯度爆炸的问题。
总的来说,ReLU是一种简单且有效的激活函数,在深度学习中被广泛使用。它能够提供非线性变换,且计算简单高效。然而,ReLU的负半轴导致的死神经元问题和梯度爆炸问题需要注意。为了解决这些问题,后续还出现了一些改进的激活函数,如Leaky ReLU、PReLU等。
nn.LeakyReLU
nn.LeakyReLU是一种改进的激活函数,它在ReLU的基础上引入了一个负半轴斜率参数。其计算公式为:
𝑦 = max(𝑥, 𝑛𝑒𝑔𝑎𝑡𝑖𝑣𝑒_𝑠𝑙𝑜𝑝𝑒 * 𝑥)
其中,𝑥是输入,𝑦是输出,𝑛𝑒𝑔𝑎𝑡𝑖𝑣𝑒_𝑠𝑙𝑜𝑝𝑒是负半轴斜率。
nn.PReLU
nn.PReLU是一种带有可学习斜率的激活函数,它在每个神经元上引入了一个学习参数。其计算公式为:
𝑦 = max(0, 𝑥) + 𝑎 * min(0, 𝑥)
其中,𝑥是输入,𝑦是输出,𝑎是可学习的斜率参数。
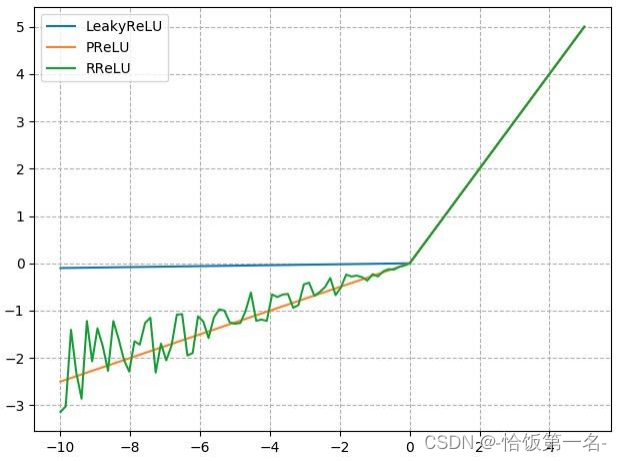
nn.RReLU
nn.RReLU是一种带有随机均匀分布斜率的激活函数,它在每个训练样本中引入了一个随机斜率。其计算公式为:
𝑦 = max(𝑥, 𝑙𝑜𝑤𝑒𝑟) + 𝑟𝑎𝑛𝑑𝑜𝑚(𝑙𝑜𝑤𝑒𝑟, 𝑢𝑝𝑝𝑒𝑟 - 𝑙𝑜𝑤𝑒𝑟) * (𝑥 - 𝑙𝑜𝑤𝑒𝑟)
其中,𝑥是输入,𝑦是输出,𝑙𝑜𝑤𝑒𝑟是均匀分布下限,𝑢𝑝𝑝𝑒𝑟是均匀分布上限,𝑟𝑎𝑛𝑑𝑜𝑚(𝑙𝑜𝑤𝑒𝑟, 𝑢𝑝𝑝𝑒𝑟)是在[𝑙𝑜𝑤𝑒𝑟, 𝑢𝑝𝑝𝑒𝑟]范围内的随机数。
这些改进的激活函数在某些情况下可以更好地处理负半轴的输入,从而缓解死神经元问题。它们的引入可以提高神经网络的性能和学习能力。

相关文章:

池化、线性、激活函数层
一、池化层 池化运算是深度学习中常用的一种操作,它可以对输入的特征图进行降采样,从而减少特征图的尺寸和参数数量。 池化运算的主要目的是通过“收集”和“总结”输入特征图的信息来提取出主要特征,并且减少对细节的敏感性。在池化运算中…...
ES-极客学习第二部分ES 入门
基本概念 索引、文档、节点、分片和API json 文档 文档的元数据 需要通过Kibana导入Sample Data的电商数据。具体参考“2.2节-Kibana的安装与界面快速浏览” 索引 kibana 管理ES索引 在系统中找到kibana配置文件(我这里是etc/kibana/kibana.yml) vim /…...

Nodejs软件安装
Nodejs软件安装 一、简介 Node.js 是一个基于 Chrome V8 引擎的 JavaScript 运行环境。 官网:http://nodejs.cn/api/ 我们关注于 node.js 的 npm 功能,NPM 是随同 NodeJS 一起安装的包管理工具,JavaScript-NPM,Java-Maven&…...
Photoshop 2024 (PS2024) v25 直装版 支持win/mac版
Photoshop 2024 提供了多种创意工具,如画笔、铅笔、涂鸦和渐变等,用户可以通过这些工具来创建独特和令人印象深刻的设计效果。增强的云同步:通过 Adobe Creative Cloud,用户可以方便地将他们的工作从一个设备无缝同步到另一个设备…...

ChatGPT绘画生成软件MidTool:智能艺术的新纪元
在人工智能的黄金时代,创新技术不断涌现,改变着我们的生活和工作方式。其中,ChatGPT绘画生成软件MidTool无疑是这一变革浪潮中的佼佼者。它不仅是一个软件,更是一位艺术家,一位智能助手,它的出现预示着智能…...

linux安装MySQL5.7(安装、开机自启、定时备份)
一、安装步骤 我喜欢安装在/usr/local/mysql目录下 #切换目录 cd /usr/local/ #下载文件 wget https://dev.mysql.com/get/Downloads/MySQL-5.7/mysql-5.7.38-linux-glibc2.12-x86_64.tar.gz #解压文件 tar -zxvf mysql-5.7.38-linux-glibc2.12-x86_64.tar.gz -C /usr/local …...

openGauss学习笔记-195 openGauss 数据库运维-常见故障定位案例-分析查询语句运行状态
文章目录 openGauss学习笔记-195 openGauss 数据库运维-常见故障定位案例-分析查询语句运行状态195.1 分析查询语句运行状态195.1.1 问题现象195.1.2 处理办法 openGauss学习笔记-195 openGauss 数据库运维-常见故障定位案例-分析查询语句运行状态 195.1 分析查询语句运行状态…...

Oracle篇—实例中和name相关参数的区别和作用
☘️博主介绍☘️: ✨又是一天没白过,我是奈斯,DBA一名✨ ✌✌️擅长Oracle、MySQL、SQLserver、Linux,也在积极的扩展IT方向的其他知识面✌✌️ ❣️❣️❣️大佬们都喜欢静静的看文章,并且也会默默的点赞收藏加关注❣…...
python + selenium 初步实现数据驱动
如果在进行自动化测试的时候将测试数据写在代码中,若测试数据有变,不利于数据的修改和维护。但可以尝试通过将测试数据放到excel文档中来实现测试数据的管理。 示例:本次涉及的项目使用的12306 selenium 重构------三层架构 excel文件数据如…...

数字孪生+可视化技术 构建智慧新能源汽车充电站监管平台
前言 充电基础设施为电动汽车提供充换电服务,是重要的交通能源融合类基础设施。近年来,随着新能源汽车产业快速发展,我国充电基础设施持续增长,已建成世界上数量最多、服务范围最广、品种类型最全的充电基础设施体系。着眼未来新…...
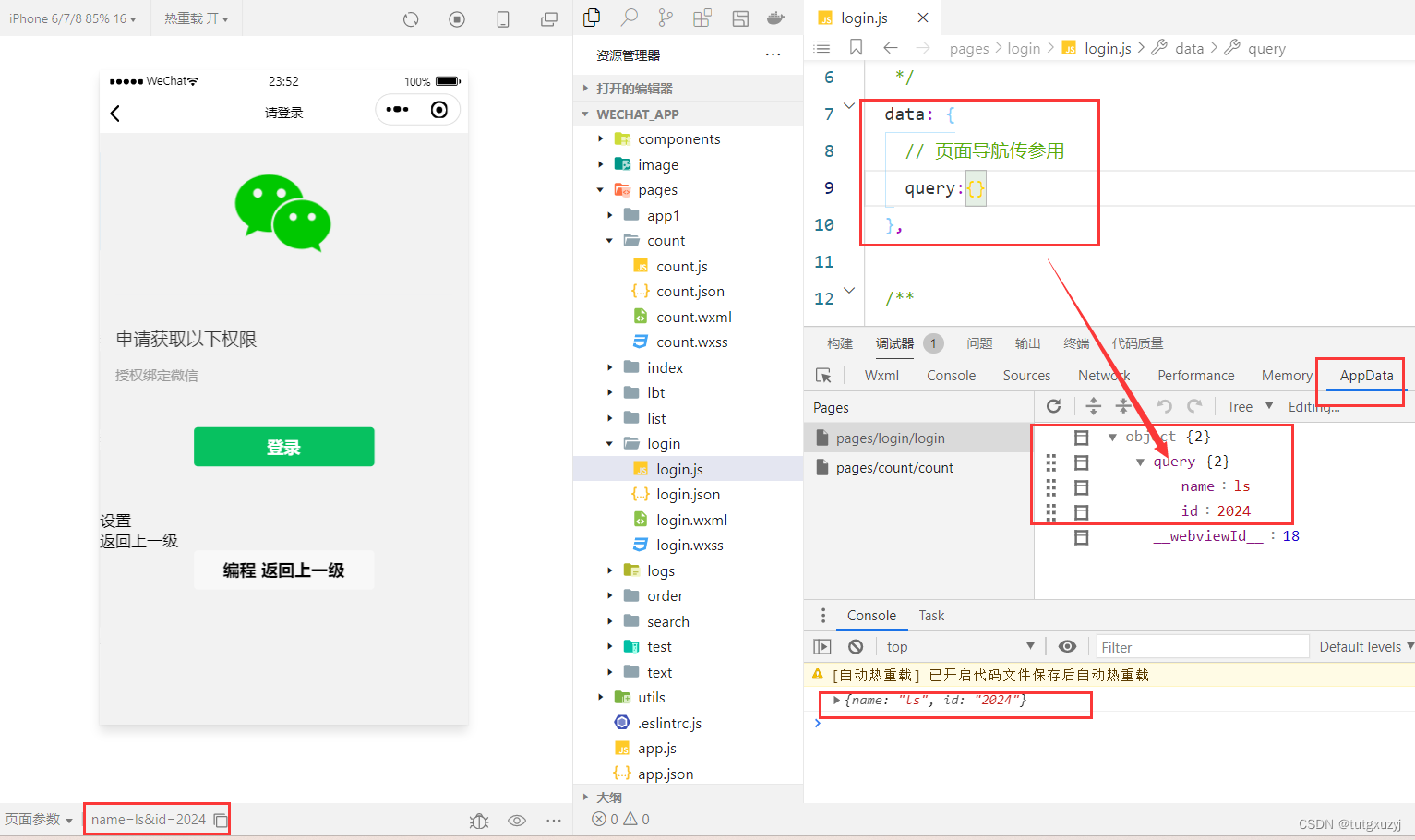
微信小程序开发学习笔记《11》导航传参
微信小程序开发学习笔记《11》导航传参 博主正在学习微信小程序开发,希望记录自己学习过程同时与广大网友共同学习讨论。导航传参 官方文档 一、声明式导航传参 navigator组件的url属性用来指定将要跳转到的页面的路径。同时,路径的后面还可以携带参数…...
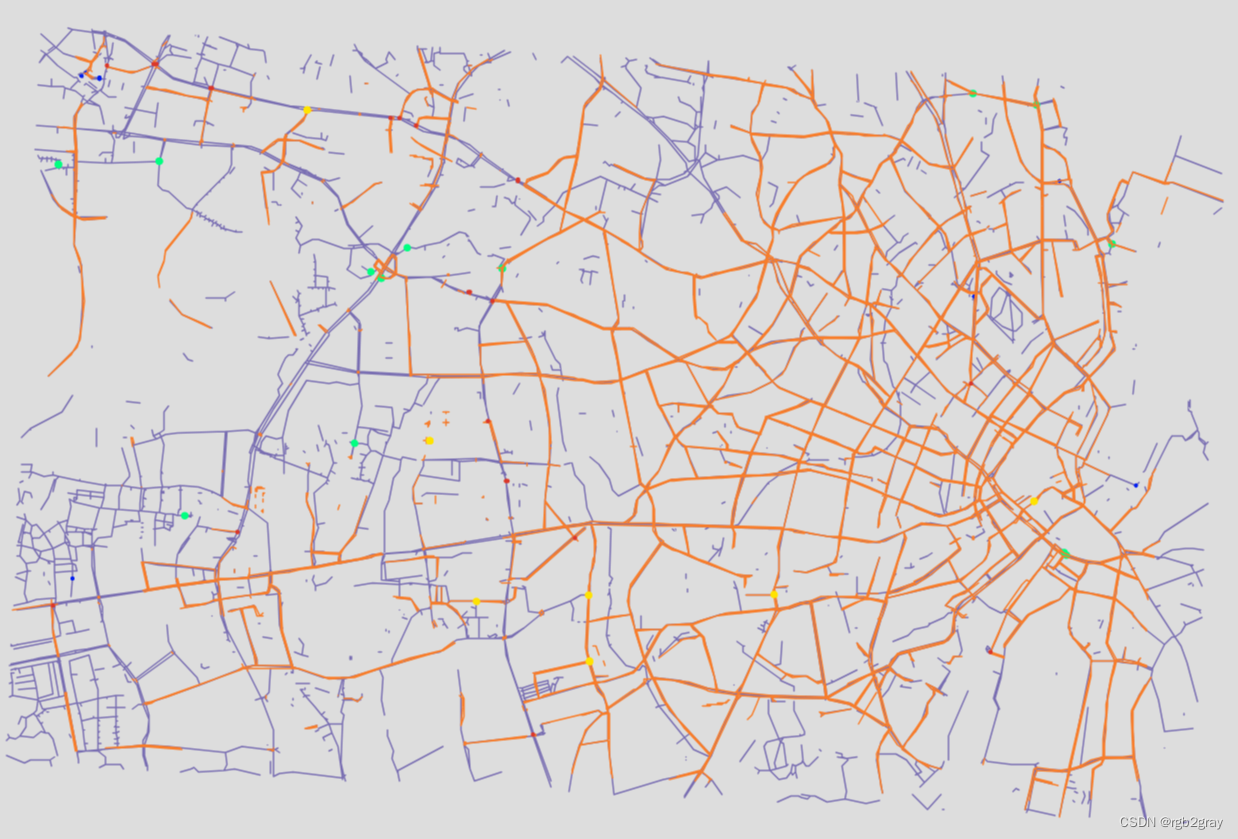
BikeDNA(七)外在分析:OSM 与参考数据的比较1
BikeDNA(七)外在分析:OSM 与参考数据的比较1 该笔记本将提供的参考自行车基础设施数据集与同一区域的 OSM 数据进行所谓的外部质量评估进行比较。 为了运行这部分分析,必须有一个参考数据集可用于比较。 该分析基于将参考数据集…...

KY43 全排列
全排列板子 ti #include<bits/stdc.h>using namespace std;string s; map<string, int>mp;void swap(char &a, char &b){char em a;a b;b em; }void dfs(int n){ //将s[n~l]的全排列转化成s[n]s[n1~l]的全排列 if(n s.length()){mp[s] 1;return ;}f…...
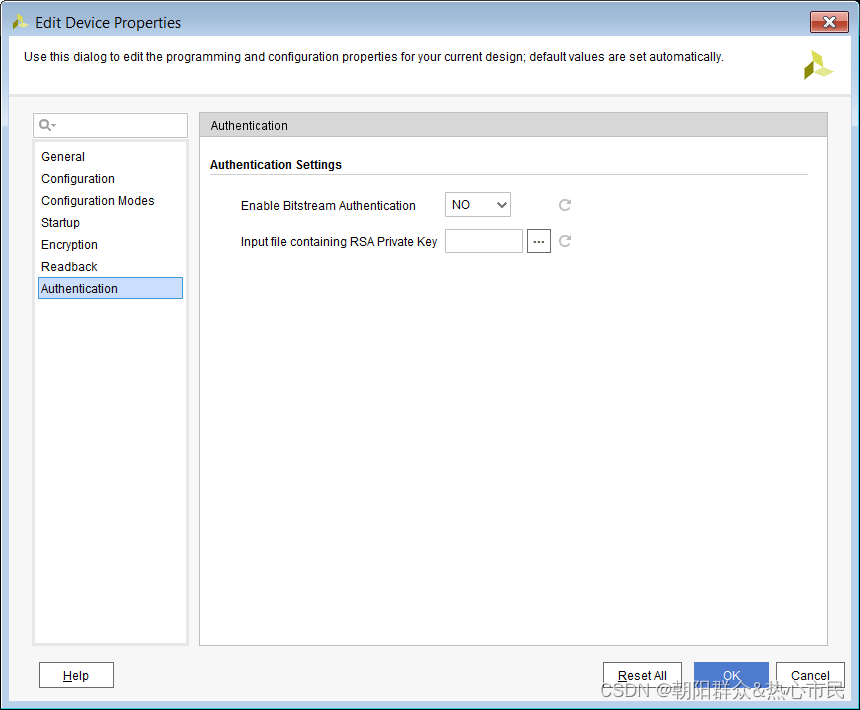
UltraScale 和 UltraScale+ 生成已加密文件和已经过身份验证的文件
注释 :如需了解更多信息,请参阅《使用加密和身份验证确保 UltraScale/UltraScale FPGA 比特流的安全》 (XAPP1267)。 要生成加密比特流,请在 Vivado IDE 中打开已实现的设计。在主工具栏中,依次选择“Flow” → “Bitstream Setti…...

2023年全国职业院校技能大赛软件测试赛题—单元测试卷②
单元测试 一、任务要求 题目1:任意输入2个正整数值分别存入x、y中,据此完成下述分析:若x≤0或y≤0,则提示:“输入不符合要求。”;若2值相同,则提示“可以构建圆形或正方形”;若2<…...
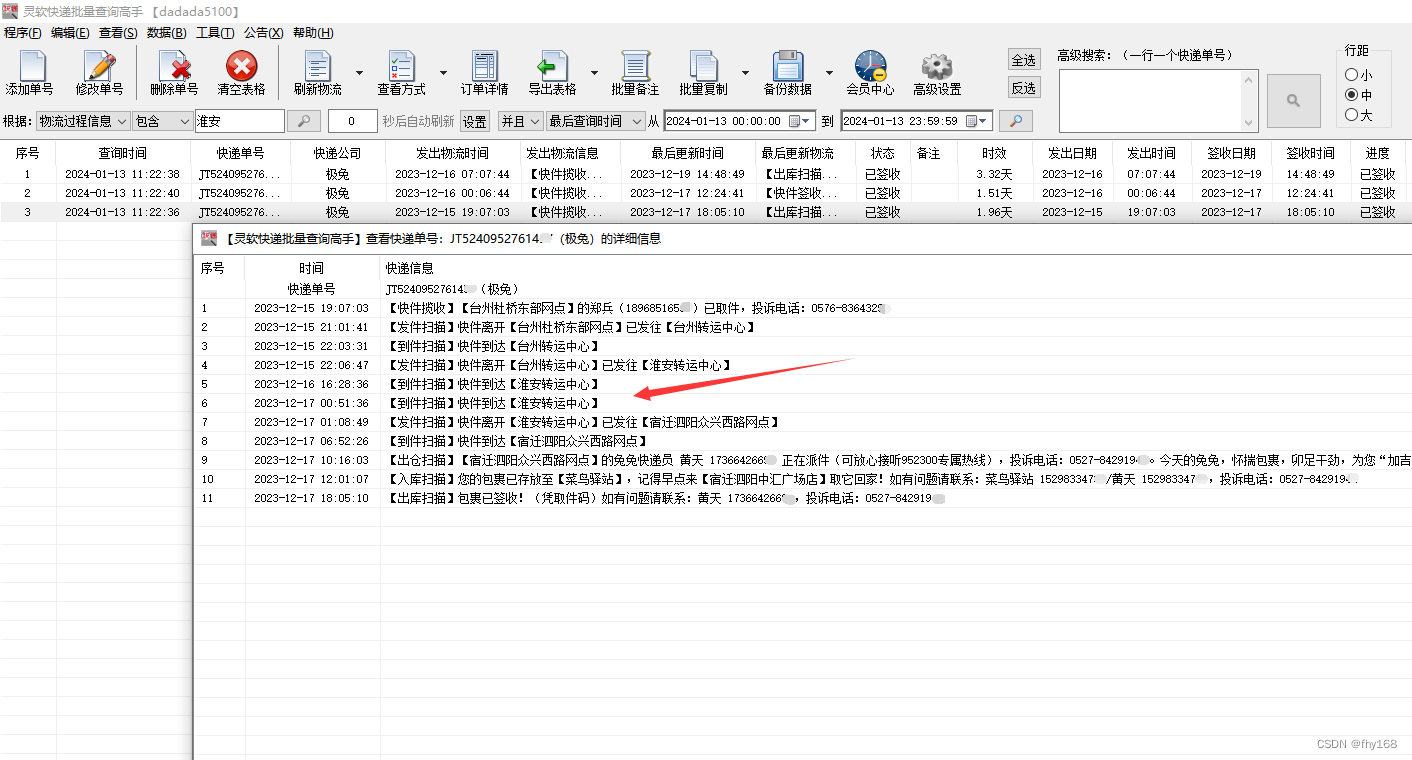
极兔单号查快递,极兔快递单号查询,筛选出途经指定城市的单号
随着电商的繁荣,快递单号已经成为我们生活中的一部分。然而,面对海量的快递信息,如何快速、准确地筛选出我们需要的单号,变成了许多人的痛点。今天,我要为你介绍一款强大的工具——快递批量查询高手,让你的…...

[redis] redis高可用之持久化
一、Redis 高可用的相关知识 1.1 什么是高可用 在web服务器中,高可用是指服务器可以正常访问的时间,衡量的标准是在多长时间内可以提供正常服务(99.9%、99.99%、99.999%等等)。 但是在Redis语境中,高可用的含义似乎要宽泛一些,…...
)
云原生 微服务 restapi devops相关的一些概念说明(持续更新中)
云原生: 定义 云原生是一种构建和运行应用程序的方法,是一套技术体系和方法论。它是一种在云计算环境中构建、部署和管理现代应用程序的软件方法。云原生应用程序是基于微服务架构的,采用开源堆栈(K8SDocker)进行容器…...
初学unity学习七天,经验收获总结
初学unity七天,经验收获总结 学习就是认识新观念和新想法的过程。 假如人们始终以同一种思维方式来考虑问题的话,那么始终只会得到同样的结果。 因为我对你讲述的许多内容是你以前从未接触过的,所以我建议你,在你还没有做之前&…...

hcip实验2
根据地址分配完成基础配置 先配置r1,r2,r3的ospf以及与isp通讯: 配置缺省路由: 完成nat配置: 完成r5,r6,r7,r8,r15的mgre以及整个网络的ospf配置 mgre: area 2 和3之间用多进程双向重发布技术完成: area4和5之间用虚…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...
