在控制理论里,单个输入变量被施加了饱和特性处理,那么后续怎么利用李雅普诺夫判据判断系统稳定性呢?
在控制理论中,当一个系统的输入变量被施加了饱和特性(即输入被限制在某个范围内),系统的稳定性分析可能变得更复杂。使用李雅普诺夫方法判断这样的系统稳定性通常需要考虑非线性特性。下面是如何使用李雅普诺夫方法进行稳定性分析的步骤,以及如何在LabVIEW中进行相关的实验和观察。
使用李雅普诺夫方法分析稳定性
-
选择或构造李雅普诺夫函数:首先需要选择或构造一个李雅普诺夫函数(V),这是一个正定函数,通常取决于系统的状态变量。
-
计算李雅普诺夫函数的导数:计算此函数关于时间的导数(V̇)。这需要考虑到系统的动力学方程和饱和特性。
-
分析李雅普诺夫函数的导数:
- 如果V̇是负定的(对于所有非零状态),则系统是全局渐进稳定的。
- 如果V̇是负半定的(不是正的),则系统可能是稳定的,但可能不是全局渐进稳定的。
- 如果V̇在某些状态下是正的,系统可能是不稳定的。
-
考虑饱和特性:在计算V̇时,需要考虑输入饱和的影响。这可能导致非线性行为,需要特别分析。
在LabVIEW中进行稳定性分析
在LabVIEW中进行稳定性分析,可以通过以下步骤进行:
-
系统模型设计:首先在LabVIEW中创建系统的模型。使用LabVIEW的控制设计和仿真工具包可以方便地建立和模拟控制系统。
-
实现饱和特性:在系统模型中实现输入的饱和特性。这可以通过使用非线性函数或特定的信号限制模块来完成。
-
李雅普诺夫函数的实现:在LabVIEW中,根据系统状态变量实现所选的李雅普诺夫函数。
-
模拟和数据收集:运行模拟,收集关于系统状态和李雅普诺夫函数值的数据。
-
分析结果:分析收集到的数据,特别是李雅普诺夫函数的值和其变化趋势。通过图形化界面可以直观地观察系统是否趋于稳定。
-
调整和优化:根据分析结果,可能需要对系统参数或李雅普诺夫函数进行调整,以确保系统的稳定性。
结合LabVIEW的示例说明
在LabVIEW中,您可以创建一个前面板来展
示系统的输入和输出,以及相关的李雅普诺夫函数值。例如,您可以使用图表来显示李雅普诺夫函数的值随时间的变化,以及系统状态变量的变化。
-
创建系统的模型:使用LabVIEW的仿真模块创建系统模型,包括饱和特性。
-
设计李雅普诺夫函数:根据系统的特点设计合适的李雅普诺夫函数,并在LabVIEW中实现。
-
模拟系统行为:运行仿真,收集系统状态和李雅普诺夫函数的数据。
-
数据展示与分析:在前面板上,用图表显示李雅普诺夫函数的时间序列,观察其是否随时间减小。如果李雅普诺夫函数的值持续减少,这通常表明系统是稳定的。
-
参数调整:基于李雅普诺夫分析的结果,调整系统参数以改善稳定性。
注意事项
- 饱和特性的引入通常会使系统分析变得更加复杂,特别是在非线性系统中。
- 在LabVIEW中,确保您的模型准确地反映了系统的物理行为,包括任何非线性特性。
- 李雅普诺夫方法提供了一种判断系统稳定性的方式,但需要仔细选择合适的李雅普诺夫函数,并准确计算其导数。
总的来说,LabVIEW提供了一个强大的平台,不仅可以用于设计和模拟复杂的控制系统,还可以用于进行稳定性分析,尤其是在涉及饱和和其他非线性特性时。通过合理设计李雅普诺夫函数和详细的仿真分析,可以有效评估并确保系统的稳定性。
相关文章:

在控制理论里,单个输入变量被施加了饱和特性处理,那么后续怎么利用李雅普诺夫判据判断系统稳定性呢?
在控制理论中,当一个系统的输入变量被施加了饱和特性(即输入被限制在某个范围内),系统的稳定性分析可能变得更复杂。使用李雅普诺夫方法判断这样的系统稳定性通常需要考虑非线性特性。下面是如何使用李雅普诺夫方法进行稳定性分析…...

MySQL夯实之路-查询性能优化深入浅出
MySQL调优分析 explain;show status查看服务器状态信息 优化 减少子任务,减少子任务执行次数,减少子任务执行时间(优,少,快) 查询优化分析方法 1.访问了太多的行和列࿱…...

UniApp面试题
面试题1 问:什么是 UniApp?它有哪些特点? 答:UniApp 是一种基于 Vue.js 开发跨平台应用的框架。它可以同时构建运行在多个平台(包括但不限于小程序、H5、App)的应用程序。UniApp 的特点包括:一…...

30 树的定义
树的定义 树的度?叶节点? 注意:k为叶节点 孩子/双亲/子孙/祖先 树的高度? 有序树 森林 树的一些操作: 粗略的框架代码: 省略。。。 小结: 树是线性表的扩展...

程序员必备的面试技巧
程序员必备的面试技巧 “程序员必备的面试技巧,就像是编写一段完美的代码一样重要。在面试战场上,我们需要像忍者一样灵活,像侦探一样聪明,还要像无敌铁金刚一样坚定。只有掌握了这些技巧,我们才能在面试的舞台上闪耀…...
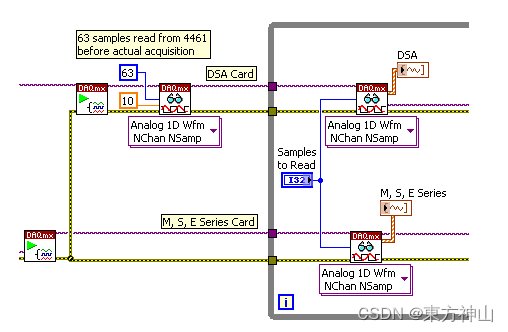
【NI-DAQmx入门】LabVIEW中DAQmx同步
1.同步解释 1.1 同步基础概念 触发器:触发器是控制采集的命令。您可以使用触发器来启动、停止或暂停采集。触发信号可以源自软件或硬件源。 时钟:时钟是用于对数据采集计时的周期性数字信号。根据具体情况,您可以使用时钟信号直接控制数据采…...

FlinkRestAPI
which flink 找到Flink客户端地址 如果输出结果为空,则说明 Flink 客户端没有安装在系统路径中。在这种情况下,您可以通过设置 FLINK_HOME 环境变量来指定 Flink 客户端的路径。例如: export FLINK_HOME/opt/flink 然后,您可以使…...

Qt获取当前系统网络接口信息
1.QInterface获取网络接口信息 void NetProperty::init() {// 获取所有网络接口const QList<QNetworkInterface> interfaces QNetworkInterface::allInterfaces();ui->com_Interface->clear();for(const QNetworkInterface& interface : interfaces){ui->…...
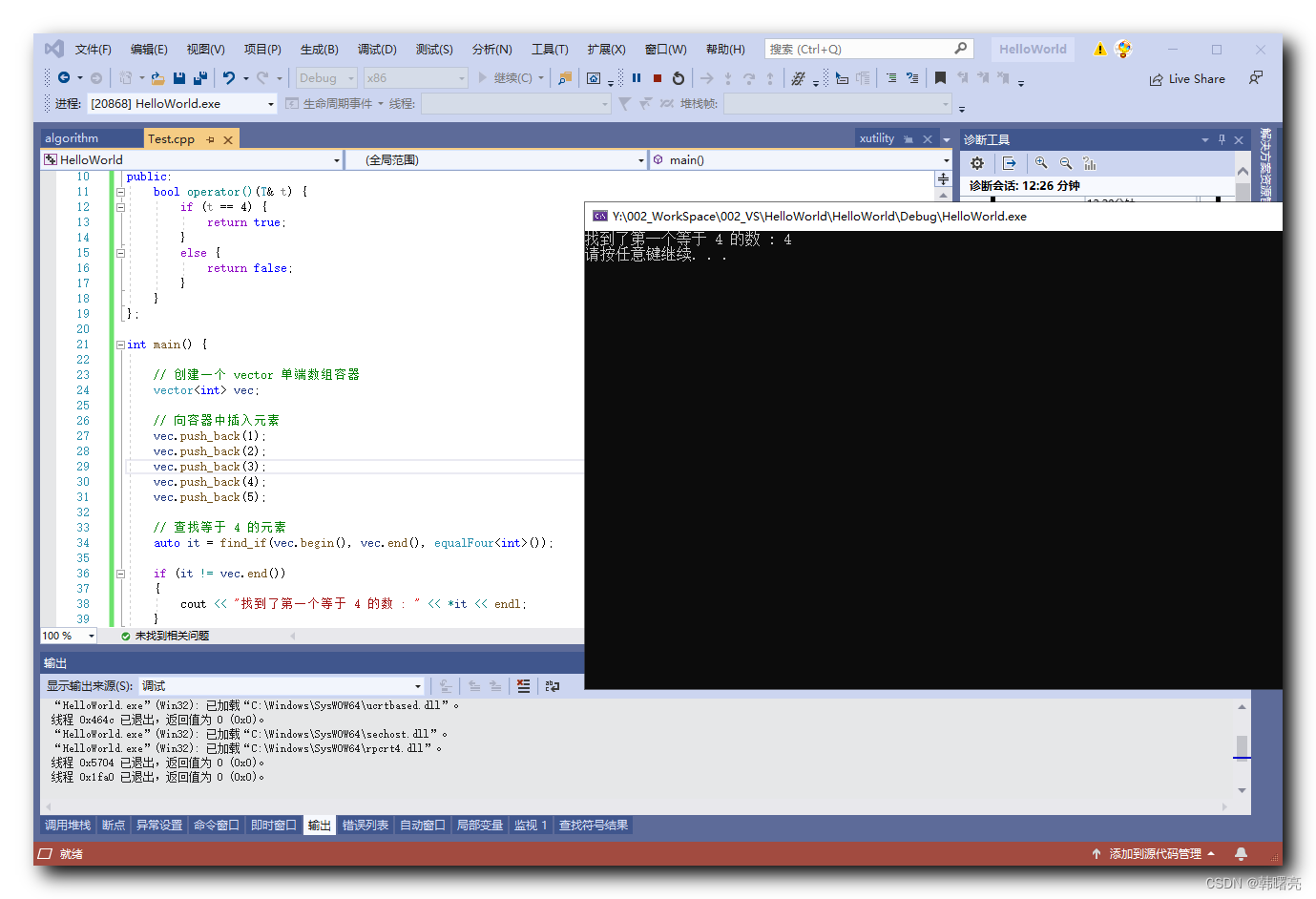
【C++】STL 算法 ④ ( 函数对象与谓词 | 一元函数对象 | “ 谓词 “ 概念 | 一元谓词 | find_if 查找算法 | 一元谓词示例 )
文章目录 一、函数对象与谓词1、一元函数对象2、" 谓词 " 概念3、find_if 查找算法 二、一元谓词示例1、代码示例 - 一元谓词示例2、执行结果 一、函数对象与谓词 1、一元函数对象 " 函数对象 " 是通过 重载 函数调用操作符 () 实现的 operator() , 函数对…...

C++ 并发编程 | 并发世界
一、C 并发世界 1、什么是并发? 并发是指两个或更多独立的活动同时发生,计算机中的并发指的是,在单个系统里同时执行多个独立的活动...

GitHub注册新账号的操作流程(详细)
目录 第一步 进入官网,点击右上角的"Sign up" 第二步 输入email地址 第三步 设置密码 第四步 输入昵称 第五步 根据个人喜好决定要不要接收GitHub的邮件推送。然后回答他们的验证问题 第六步 输入验证码 我在注册github账号时遇到过一些阻碍&#x…...

Kali安装Xrdp结合内网穿透实现无公网ip远程访问系统桌面
文章目录 前言1. Kali 安装Xrdp2. 本地远程Kali桌面3. Kali 安装Cpolar 内网穿透4. 配置公网远程地址5. 公网远程Kali桌面连接6. 固定连接公网地址7. 固定地址连接测试 前言 Kali远程桌面的好处在于,它允许用户从远程位置访问Kali系统,而无需直接物理访…...

【WEB API自动化测试】接口文档与在线测试
这一篇我们主要介绍如何做API帮助文档,给API的调用人员介绍各个 API的功能, 输入参数,输出参数, 以及在线测试 API功能(这个也是方便我们自己开发调试) 我们先来看看我们的API最终帮助文档及在线测试最终达到的效果: 概要图 GET API 添加产品API: 删除…...

【深度学习每日小知识】Training Data 训练数据
训练数据是机器学习的基本组成部分,在模型的开发和性能中起着至关重要的作用。它是指用于训练机器学习算法的标记或注释数据集。以下是与训练数据相关的一些关键方面和注意事项。 Quantity 数量 训练数据的数量很重要,因为它会影响模型的泛化能力。通常…...

[acm算法学习] 后缀数组SA
学习自B站up主 kouylan 定义 后缀是包含最后个字母的子串 把字符串 str 的所有后缀按字典排序,sa[i]表示排名为 i 的后缀的开头下标 如何求解SA 倍增的方法 先把每个位置开始的长度为1的子串排序,在此基础上再把长度为2的子串排序(长度…...

DNS解析和它的三个实验
一、DNS介绍 DNS:domain name server 7层协议 名称解析协议 tcp /53 主从之间的同步 udp/53 名字解析 DNS作用:将域名转换成IP地址的协议 1.1DNS的两种实现方式 1.通过hosts文件(优先级最高) 分散的管理 linux /etc/hos…...
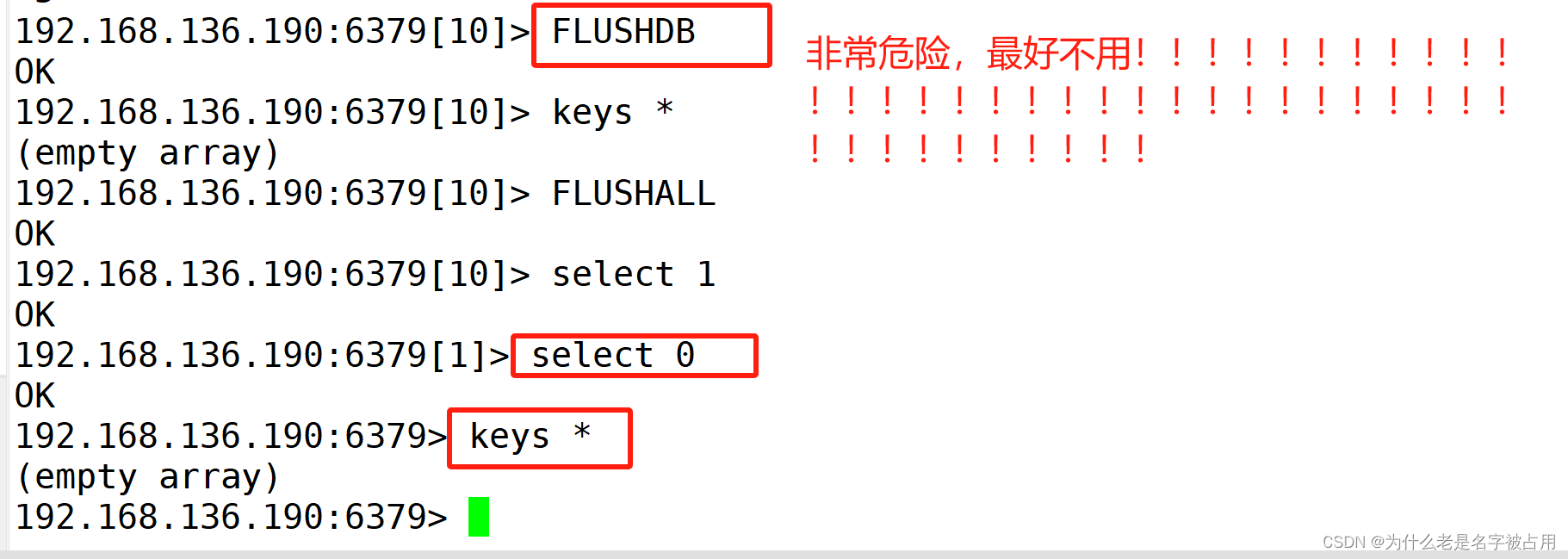
[redis] redis的安装,配置与简单操作
一、缓存的相关知识 1.1 缓存的概念 缓存是为了调节速度不一致的两个或多个不同的物质的速度,在中间对速度较慢的一方起到加速作用,比如CPU的一级、二级缓存是保存了CPU最近经常访问的数据,内存是保存CPU经常访问硬盘的数据,而且…...

C++ STL set容器
和 map、multimap 容器不同,使用 set 容器存储的各个键值对,要求键 key 和值 value 必须相等。 举个例子,如下有 2 组键值对数据: {<a, 1>, <b, 2>, <c, 3>} {<a, a>, <b, b>, <c, c>} 显然&…...

专业课148,总分410+电子科技大学858信号与系统考研经验电子信息与通信
今年专业课148分,总分410顺利被电子科技大学录取,回望这一年复习还有很多不足,总结一下自己的复习经历,希望对大家复习有所帮助。 数学:(多动手,多计算,多总结,打好基础…...
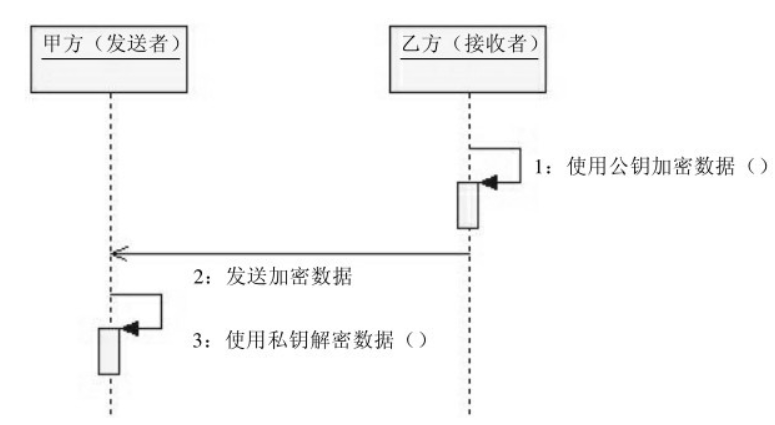
密码学:一文读懂非对称加密算法 DH、RSA
文章目录 前言非对称加密算法的由来非对称加密算法的家谱1.基于因子分解难题2.基于离散对数难题 密钥交换算法-DH密钥交换算法-DH的通信模型初始化DH算法密钥对甲方构建DH算法本地密钥乙方构建DH算法本地密钥DH算法加密消息传递 典型非对称加密算法-RSARSA的通信模型RSA特有的的…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
