数据结构与算法教程,数据结构C语言版教程!(第三部分、栈(Stack)和队列(Queue)详解)六
第三部分、栈(Stack)和队列(Queue)详解

栈和队列,严格意义上来说,也属于线性表,因为它们也都用于存储逻辑关系为 "一对一" 的数据,但由于它们比较特殊,因此将其单独作为一章,做重点讲解。
使用栈结构存储数据,讲究“先进后出”,即最先进栈的数据,最后出栈;使用队列存储数据,讲究 "先进先出",即最先进队列的数据,也最先出队列。
既然栈和队列都属于线性表,根据线性表分为顺序表和链表的特点,栈也可分为顺序栈和链表,队列也分为顺序队列和链队列,这些内容都会在本章做详细讲解。
十一、[数据结构实践项目]扑克牌游戏(包含C语言实现代码)
小时候在刚开始接触扑克牌的时候,最初学会的扑克游戏就是类似于“推小车”这样的无脑游戏,本节带领大家使用学过的知识编写推小车卡牌游戏。
“推小车”扑克牌游戏适合 2-3 个人玩,游戏规则也超级简单:将一副扑克牌平均分成两份,每人拿一份,每个人手中的扑克牌全部反面朝上,叠成一摞。游戏进行时,每个人轮流拿出第一张扑克牌放到桌上,将其排成一竖行。如果打出的牌与桌上某张牌的数字(红桃 5 和黑桃 5 在此游戏中相等)相等,即可将两张相同的牌以及两张中间所夹的所有的牌全部取走,每次取走的一小摞牌都必须放到自己本摞的下面。
游戏过程中,一旦有人手中没有牌,则宣布另一人获胜,同时游戏结束。
1、设计思路
假设模拟两个人进行该扑克牌游戏。每个人在游戏过程中都是不断地从自己这一摞扑克牌的最上方去取牌,放到桌子上;当发现自己的牌同桌子上的牌相等时,将赢得的牌依次放在自己扑克牌的下方。这是典型的队列的“先进先出”。
而对于桌子而言,就相当于是一个栈。每次放到桌子上的扑克牌,都相当于进栈;当有相同的扑克牌时,相同的扑克牌连通之间的所有的扑克牌则依次出栈。
所以,模拟该扑克牌游戏需要同时使用 2 个队列和 1 个栈。
2、实现代码
#include <stdio.h>
#include <stdlib.h>
struct queue
{
int data[1000];
int head;
int tail;
};
struct stack
{
int data[10];
int top;
};
void showCard(struct queue *q,int *book,struct stack *s){
int t=(*q).data[(*q).head]; //打出一张牌,即从队列 q 的队头取元素(此时还不往桌子的栈里放)
//判断取出的这张牌是否会赢牌
if(book[t]==0){ //若不赢牌,只需放到桌子上入栈即可
(*q).head++;//由于此时牌已经打出,所以队列的队头需要前进
(*s).top++;
(*s).data[(*s).top]=t; //再把打出的牌放到桌上,即入栈
book[t]=1; //标记桌上现在已经有牌面为t的牌
}
else{
(*q).head++;//由于此时已经打出去一张牌,所以队头需要 +1
(*q).data[(*q).tail]=t;//将打出的牌放到手中牌的最后(再入队)
(*q).tail++;
//把桌子上赢得的牌依次放到手中牌的最后(依次出栈在入队列的过程)
while((*s).data[(*s).top]!=t){
book[(*s).data[(*s).top]]=0;//取消对该牌号的标记
(*q).data[(*q).tail]=(*s).data[(*s).top];//依次放入队尾
(*q).tail++;
(*s).top--;
}
//最后别忘了将最后一张相等的牌取出放入队列
book[(*s).data[(*s).top]]=0;
(*q).data[(*q).tail]=(*s).data[(*s).top];
(*q).tail++;
(*s).top--;
}
}
int main() {
struct queue q1,q2;//两个队列,分别模拟两个人,假设分别为小王和小李
struct stack s;//栈,模拟桌子
int book[14];//为了便于判断桌子上的牌是否有相同的,增加一个数组用于判断
int i;
//初始化队列
q1.head=0; q1.tail=0;
q2.head=0; q2.tail=0;
//初始化栈
s.top=-1;
//初始化用来标记的数组
for(i=0;i<=13;i++)
book[i]=0;
//假设初期每个人手中仅有 6 张牌,每个人拥有的牌都是随机的,但都在 1-13 之间
for(i=1;i<=6;i++){
q1.data[q1.tail]=rand()%13+1;
q1.tail++;
}
for(i=1;i<=6;i++){
q2.data[q2.tail]=rand()%13+1;
q2.tail++;
}
//仅当其中一个人没有牌时,游戏结束
while(q1.head<q1.tail && q2.head<q2.tail ){ showCard(&q2, book, &s);//小李出牌
showCard(&q1, book, &s);//小王出牌
}
//游戏结束时,输出最后的赢家以及手中剩余的牌数
if(q2.head==q2.tail){
printf("小李赢\n");
printf("手中还有:%d 张牌",q1.tail-q1.head);
}
else{
printf("小王赢\n");
printf("手中还有:%d 张牌",q2.tail-q2.head);
}
return 0;
}
运行结果:
小王赢
手中还有:7 张牌
十二、栈和队列是线性结构(包含栈和队列的区别和共同点)
很多学员问,栈和队列是线性结构吗?这里再次强调,栈和队列是线性结构。
数据结构中,如果想知道存储结构之间是否相同和类似,只需要比对它们存储的目标数据之间的逻辑关系即可,所存储数据的逻辑关系相同,则说明它们是同一类存储结构;反之,则不是。
通过前面的学习我们知道,线性结构,即用于存储逻辑关系为 "一对一" 数据的存储结构,例如顺序存储结构和链式存储结构。
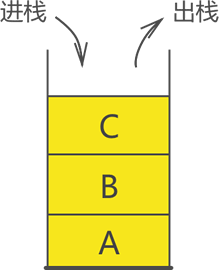
图 1 栈存储结构
回过头再分析栈(如图 1 所示),栈结构中存储的也是逻辑关系为 "一对一" 的数据,只不过该结构对数据的存储顺序有额外的要求,即数据进栈和出栈要满足 "先进后出" 的要求。因此可以这么说,栈是一种特殊的线性存储结构。

图 2 队列存储结构
那么,队列存储结构(如图 2 所示)呢?同栈一样,它存储的也是逻辑关系为 "一对一" 的数据,但它对数据入队和出队的要求是 "先进先出"。所以说,队列也是一种特殊的线性存储结构。
总的来说,栈和队列是线性存储结构,只不过它们比较 "特殊" 而已。
栈和队列,除了都是线性结构外,还有一个共同点,那就是数据的进出,只能在栈和队列的端点处进行。换句话说,栈结构中,数据的入栈和出栈只能在开口的一端进行;队列中,数据从一端进,从另一端出。
栈和队列最大的区别就是,栈结构中存储数据要求 "先进后出";队列存储数据要求 "先进先出"。
相关文章:

数据结构与算法教程,数据结构C语言版教程!(第三部分、栈(Stack)和队列(Queue)详解)六
第三部分、栈(Stack)和队列(Queue)详解 栈和队列,严格意义上来说,也属于线性表,因为它们也都用于存储逻辑关系为 "一对一" 的数据,但由于它们比较特殊,因此将其单独作为一章,做重点讲解。 使用栈…...

使用Docker部署PDF多功能工具Stirling-PDF
1.服务器上安装docker 安装比较简单,这种安装的Docker不是最新版本,不过对于学习够用了,依次执行下面命令进行安装。 sudo apt install docker.io sudo systemctl start docker sudo systemctl enable docker 查看是否安装成功 $ docker …...

linux安装系统遇到的问题
这两天打算攻克下来网络编程,发现这也确实是很重要的一个东西,但我就奇了怪了,老师就压根没提,反正留在我印象的就一个tcp/ip七层网络。也说正好,把linux命令也熟悉熟悉,拿着我大一课本快速过过 连接cento…...

groovy XmlParser 递归遍历 xml 文件,修改并保存
使用 groovy.util.XmlParser 解析 xml 文件,对文件进行修改(新增标签),然后保存。 是不是 XmlParser 没有提供方法遍历每个节点,难道要自己写? 什么是递归? 不用说,想必都懂得~ …...
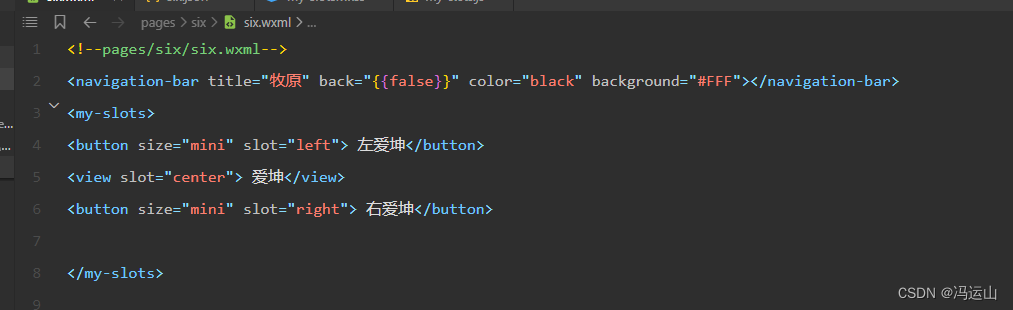
小程序基础学习(多插槽)
先创建插槽 定义多插槽的每一个插槽的属性 在js文件中启用多插槽 在页面使用多插槽 组件代码 <!--components/my-slots/my-slots.wxml--><view class"container"><view class"left"> <slot name"left" ></slot>&…...
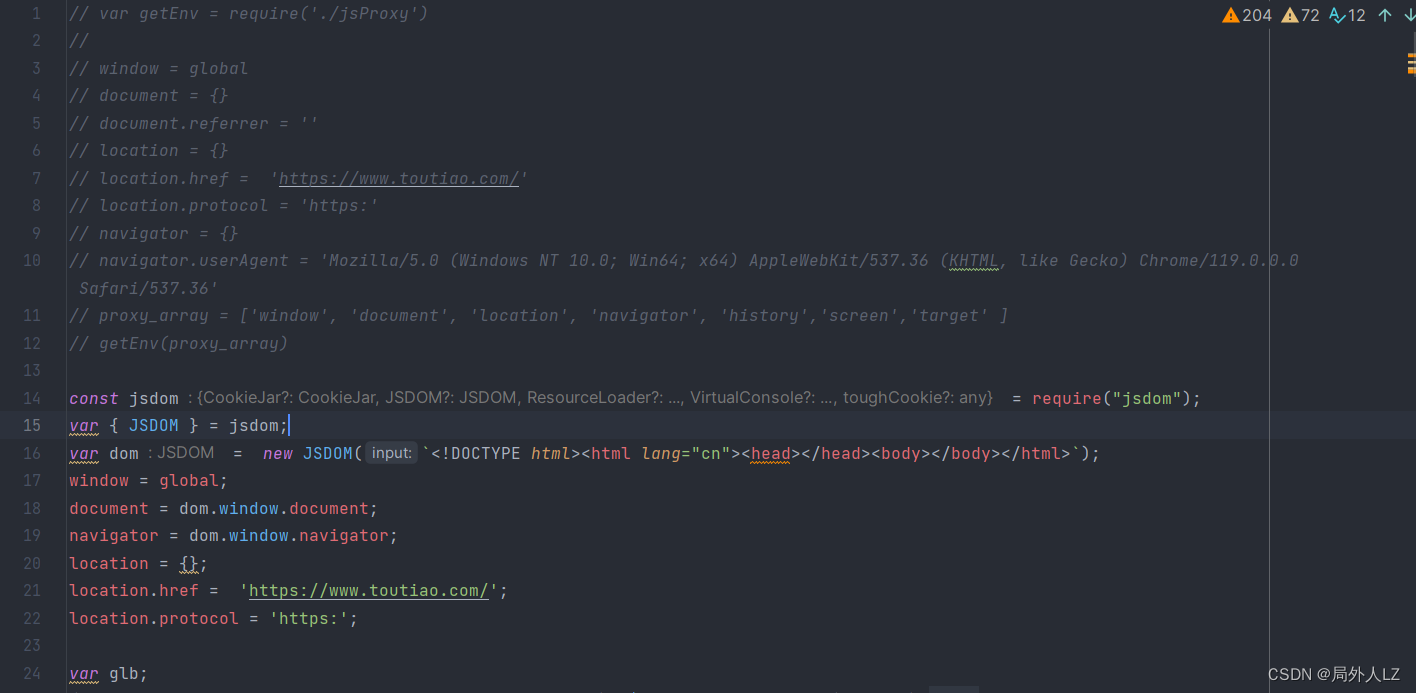
爬虫补环境jsdom、proxy、Selenium案例:某条
声明: 该文章为学习使用,严禁用于商业用途和非法用途,违者后果自负,由此产生的一切后果均与作者无关 一、简介 爬虫逆向补环境的目的是为了模拟正常用户的行为,使爬虫看起来更像是一个真实的用户在浏览网站。这样可以…...

电子学会C/C++编程等级考试2021年09月(四级)真题解析
C/C++编程(1~8级)全部真题・点这里 第1题:最佳路径 如下所示的由正整数数字构成的三角形: 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5 从三角形的顶部到底部有很多条不同的路径。对于每条路径,把路径上面的数加起来可以得到一个和,和最大的路径称为最佳路径。你的任务就是求出最佳路径…...

DevExpress历史安装文件包集合
Components - DevExpress.NET组件安装包此安装程序包括所有 .NET Framework、.NET Core 3 和 .NET 5、ASP.NET Core 和 HTML/JavaScript 组件和库(Web和桌面应用程序开发只需要安装此文件即可)。 注意:自DevExpress21.1版本之后,该…...

科技云报道:“存算一体”是大模型AI芯片的破局关键?
科技云报道原创。 在AI发展历史上,曾有两次“圣杯时刻”。 第一次发生在2012年10月,卷积神经网络(CNN)算法凭借比人眼识别更低的错误率,打开了计算机视觉的应用盛世。 第二次是2016年3月,DeepMind研发的…...

watch监听一个对象中的属性 - Vue篇
vue中提供了watch方法,可以监听data内的某些数据的变动,触发相应的方法。 1.监听一个对象 <script>export default {data() {return {obj: {name: ,code: ,timePicker:[]}}},watch: {obj: {handler(newVal, oldVal) {//todo},immediate: true,deep…...
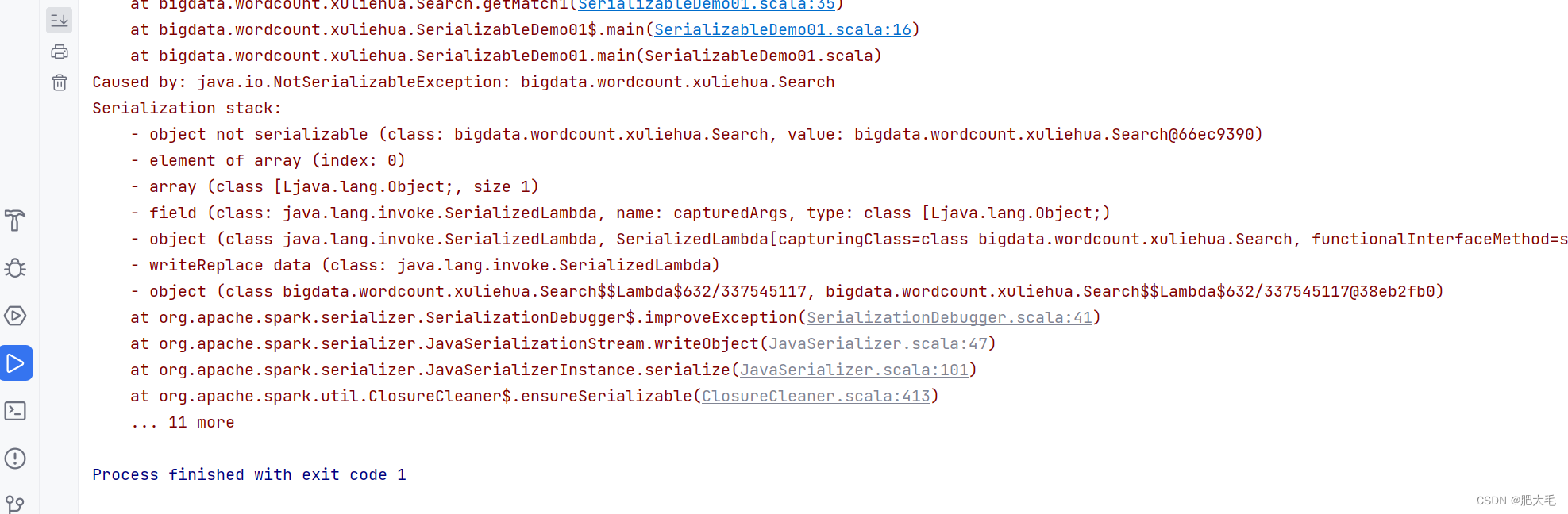
Spark---RDD序列化
文章目录 1 什么是序列化2.RDD中的闭包检查3.Kryo 序列化框架 1 什么是序列化 序列化是指 将对象的状态信息转换为可以存储或传输的形式的过程。 在序列化期间,对象将其当前状态写入到临时或持久性存储区。以后,可以通过从存储区中读取或反序列化对象的…...

Xtuner大模型微调
Xtuner大模型微调 一、课程笔记 文档链接:https://github.com/InternLM/tutorial/blob/main/xtuner/README.md 视频链接: https://www.bilibili.com/video/BV1yK4y1B75J/ 大模型微调 大模型的训练利用了各类数据,可以说是一个通才ÿ…...

JavaScript基础04
1 - 数组 1.1 数组的概念 数组可以把一组相关的数据一起存放,并提供方便的访问(获取)方式。 数组是指一组数据的集合,其中的每个数据被称作元素,在数组中可以存放任意类型的元素。数组是一种将一组数据存储在单个变量名下的优雅…...
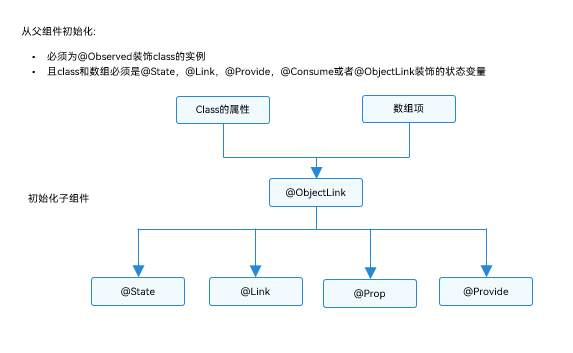
HarmonyOS@Observed装饰器和@ObjectLink装饰器:嵌套类对象属性变化
Observed装饰器和ObjectLink装饰器:嵌套类对象属性变化 上文所述的装饰器仅能观察到第一层的变化,但是在实际应用开发中,应用会根据开发需要,封装自己的数据模型。对于多层嵌套的情况,比如二维数组,或者数…...

x-cmd pkg | jless - 受 Vim 启发的命令行 JSON 查看器
目录 简介首次用户功能特点类似工具与竞品进一步探索 简介 jless 是一个命令行 JSON 查看器,设计用于读取、探索和搜索 JSON 数据。可以使用它来替代 less 、 jq 、 cat 以及您当前用于查看 JSON 文件的编辑器的任何组合。它是用 Rust 编写的,可以作为单…...

【HuggingFace Transformer库学习笔记】基础组件学习:Datasets
基础组件——Datasets datasets基本使用 导入包 from datasets import *加载数据 datasets load_dataset("madao33/new-title-chinese") datasetsDatasetDict({train: Dataset({features: [title, content],num_rows: 5850})validation: Dataset({features: [titl…...

[机缘参悟-126] :实修 - 从系统论角度理解自洽的人生:和谐、稳定,不拧巴,不焦虑,不纠结
目录 一、从系统论理解自洽 1.1 什么是系统 1.2 什么是自洽 1.3 什么是不自洽 1.4 为什么要自洽 1.5 不自洽的系统面临的挑战 二、人生需要自洽 2.1 人生自洽的意义 2.2 一个不自洽的人生会怎么样? 2.3 不自洽的特征 2.4 不自洽的人没有稳定的人格 三、…...

慢 SQL 的优化思路
分析慢 SQL 如何定位慢 SQL 呢? 可以通过 slow log 来查看慢SQL,默认的情况下,MySQL 数据库是不开启慢查询日志(slow query log)。所以我们需要手动把它打开。 查看下慢查询日志配置,我们可以使用 show …...

强化学习(一)简介
强化学习这一概念在历史上来源于行为心理学,来描述生物为了趋利避害而改变自己行为的学习过程。人类学习的过程其实就是为达到某种目的不断地与环境进行互动试错,比如婴儿学习走路。强化学习算法探索了一种从交互中学习的计算方法。 1、强化学习 强化学…...

外贸常用网站
外贸常用网站 网站阿里巴巴国际站阿里巴巴国内站Aliexpress 速卖通shopifyAmazon 亚马逊k3 开山女鞋网bao66 牛包包网爱搜鞋k3 开山网(女鞋)新款网(男女鞋)搜款网(男女衣服)17zwd(女装)17zwd(女装) 物流yunexpress 云途物流 其他amz123 跨境卖家导航amz520 跨境卖家导航 网站 …...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
