vue3环境下,三方组件中使用echarts,无法显示问题
问题描述:
vue3中,使用了三方组件primevue的侧边栏Sidebar,在其中注册echarts dom节点,无法显示,提示dom不存在
问题分析:
使用原生div,通过document.getElementById(''),将echarts注册其中,发现可以正常显示;
使用primevue的sidebar,在其中注册div,则无法获取
问题原因:
三方组件还未渲染该节点,所以找不到echarts要绑定的dom
解决方法:
await nextTick()后,开始注册echarts dom,此时三方组件中的dom才能被找到
具体实现:
<template>
<Sidebarv-model:visible="visibleRight"header="Right Sidebar"position="right"class="w-full md:w-10 lg:w-8"><div class="flex align-items-center justify-content-center h-full"><div ref="echartsDom"></div></div>
</Sidebar>
</template>
<script setup>
import { ref } from 'vue';const echartsDom = ref(null)
await nextTick();
var myChart = echarts.init(echartsDom.value, null, {width: 700,height: 500,
});
// 绘制图表
myChart.setOption({title: {text: "变更问题分类",},tooltip: {},xAxis: {axisLabel: {ormatter: "{value}",align: "left",rotate: -45,},data: ["101 尺寸","102 结构","103 材料","104 装调验证","105 外购件","106 间接返修","107 成本","108 客户变更","109 改造项目",],},yAxis: {},series: [{name: "问题单数",type: "bar",data: [1, 2, 3, 4, 5, 6, 7, 8, 19],},],
});
</script>相关文章:

vue3环境下,三方组件中使用echarts,无法显示问题
问题描述: vue3中,使用了三方组件primevue的侧边栏Sidebar,在其中注册echarts dom节点,无法显示,提示dom不存在 问题分析: 使用原生div,通过document.getElementById(),将echarts…...
FAST OS DOCKER 可视化Docker管理工具
介绍 FAST OS DOCKER 界面直观、简洁,非常适合新手使用,方便大家轻松上手 docker部署运行各类有趣的容器应用,同时 FAST OS DOCKER 为防止服务器负载过高,进行了底层性能优化;其以服务器安全为基础,对其进…...

MOJO基础语法
文章目录 打印变量及方法声明结构体python集成 打印 print("Hello Mojo!")变量及方法声明 变量: 使用’ var ‘创建一个可变的值,或者用’ let 创建一个不可变的值。 方法: 方法可以使用python中的def 方法声明,也引…...

java基础之IO流之字符流
字符流 传输char和String类型的数据 输入流 抽象父类:Reader 节点流:FileReader 常用方法 int read():读取一个字符,读取到达末尾,返回-1 package com.by.test2; import java.io.FileNotFoundException; import…...
-mojo binding)
chromium通信系统-ipcz系统(十一)-mojo binding
关于mojo binding的官方文档为mojo docs。 由于比较复杂,这里只做简单源码分析。 我们知道要实现rpc,必须实现客户端和服务端。 mojo 实现了一套领域语言,通过领域语言描述接口和数据, 再通过特有编译器编译成c代码。 这个过程会…...
鸿蒙开发基础-Web组件之cookie操作
使用ArkTS语言实现一个简单的免登录过程,向大家介绍基本的cookie管理操作。主要包含以下功能: 获取指定url对应的cookie的值。设置cookie。清除所有cookie。免登录访问账户中心。 cookie读写操作 首次打开应用时,应用首页的Web组件内呈现的…...

什么是k8s和声明式编程?
认识k8s之后,他的操作模式对我来说是一种很不错的体验。他提供了更接近现实世界的面向对象接口。 什么是k8s? Kubernetes(K8s)是一种开源容器编排平台,用于自动化部署、扩展和管理容器化应用程序。它简化了容器化应用…...
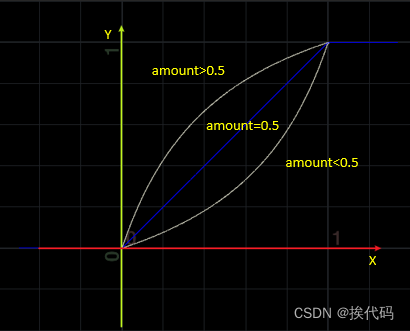
Fluids —— MicroSolvers DOP
目录 Gas SubStep —— 重复执行对应的子步 Switch Solver —— 切换解算器 Gas Attribute Swap —— 交换、复制或移动几何体属性 Gas Intermittent Solve —— 固定时间间隔计算子解算器 Gas External Forces —— 计算外部力并更新速度或速度场 Gas Particle Separate…...

工业智能网关:HiWoo Box远程采集设备数据
工业智能网关:HiWoo Box远程采集设备数据 在工业4.0和智能制造的浪潮下,工业互联网已成为推动产业升级、提升生产效率的关键。而在这其中,工业智能网关扮演着至关重要的角色。今天,我们就来深入探讨一下工业智能网关。 一、什么…...

Apollo之原理和使用讲解
文章目录 1 Apollo1.1 简介1.1.1 背景1.1.2 简介1.1.3 特点 1.2 基础模型1.3 Apollo 四个维度1.3.1 application1.3.2 environment1.3.3 cluster1.3.4 namespace 1.4 本地缓存1.5 客户端设计1.5.1 客服端拉取原理1.5.2 配置更新推送实现 1.6 总体设计1.7 可用性考虑 2 操作使用…...
魅族MX4pro系统升级、降级
网上的教程都是按住开机键音量上或者下键,但是我按了没用,还是直接点击压缩包管用。 下载系统 官网地址(所有手机固件):https://flyme.cn/firmware.html 官方魅族mx4Pro系统:https://flyme.cn/firmwarelis…...

【Docker】快速入门之Docker的安装及使用
一、引言 1、什么是Docker Docker是一个开源的应用容器引擎,它让开发者可以将他们的应用及其依赖打包到一个可移植的镜像中,然后发布到任何流行的Linux或Windows操作系统的机器上,也可以实现虚拟化。容器是完全使用沙箱机制,相互之…...

记录汇川:H5U于Factory IO测试13
主程序: 子程序: IO映射 子程序: 辅助出料 子程序: 模式选择 子程序: 示教程序 子程序: 手动程序 子程序: 统计程序 子程序: 异常报警 子程序: 自动程序: F…...

PYTHON通过跳板机巡检CENTOS的简单实现
实现的细节和引用的文件和以前博客记录的基本一致 https://shaka.blog.csdn.net/article/details/106927633 差别在于,这次是通过跳板机登陆获取的主机信息,只记录差异的部份 1.需要在跳板机相应的路径放置PYTHON的脚本resc.py resc.py这个脚本中有引用的文件(pm.sh,diskpn…...

网络配置以及命令详解
传统linux中,网络接口为eth0,eth1,eth2,..... RHEL 7以上版本默认命名是基于分配上的固定名称,ens33 接口类型: en:以太网有线接口 wl:无线局域网接口 ww:无线广域网 dmesg:显示开机信息 适配器类型: s:热插拔插槽 o:板载 p:pci类型 ifconfig ens160(命令行配置,临时生效):查…...

商务外语MR混合现实仿真情景实训教学
MR混合现实技术是一种将虚拟世界与真实世界相结合的技术。通过MR设备,我们可以将虚拟的场景、人物、物品等元素实时地呈现在真实的环境中,实现真实与虚拟的完美融合。在商务外语的实训教学中,MR技术可以为我们提供丰富的场景资源,…...

牛客周赛 Round 28 解题报告 | 珂学家 | 组合数学 + 离散化树状数组
前言 整体评价 还是E稍微有点意思,新周赛好像比预期要简单一些, _. 欢迎关注 珂朵莉 牛客周赛专栏 珂朵莉 牛客小白月赛专栏 A. 小红的新周赛 思路: 模拟 #include <bits/stdc.h>using namespace std;int main() {int res 0;for (int i 0; i < 6; i…...
—— 变量)
Python系列(3)—— 变量
变量 一、变量命名规范二、变量赋值三、变量的数据类型四、变量的作用域五、变量类型转换 Python编程中,变量是存储数据的容器。它们用于存储各种数据类型,如整数、浮点数、字符串、列表、字典等。理解变量及其工作原理是Python编程的基础。 一、变量命…...

Java 并发性和多线程2
四、如何创建并运行 java 线程 Java 线程类也是一个 object 类,它的实例都继承自 java.lang.Thread 或其子类。 可以用如下方式用 java 中创建一个线程: Tread thread new Thread(); 执行该线程可以调用该线程的 start()方法: thread.start(); 在上…...
最新消息:OpenAI GPT Store 正式上线,GPTs 应用商店来了!
原文链接 https://openaigptguide.com/gpt-store-and-chatgpt-team/ OpenAI推出的两款新产品和服务:GPT Store和ChatGPT Team,提供了许多全新的解决方案和功能,旨在帮助用户更轻松地使用和构建GPT工具,同时也增加了公司的收入来源…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...

linux设备重启后时间与网络时间不同步怎么解决?
linux设备重启后时间与网络时间不同步怎么解决? 设备只要一重启,时间又错了/偏了,明明刚刚对时还是对的! 这在物联网、嵌入式开发环境特别常见,尤其是开发板、树莓派、rk3588 这类设备。 解决方法: 加硬件…...
)
零基础在实践中学习网络安全-皮卡丘靶场(第十一期-目录遍历模块)
经过前面几期的内容我们学习了很多网络安全的知识,而这期内容就涉及到了前面的第六期-RCE模块,第七期-File inclusion模块,第八期-Unsafe Filedownload模块。 什么是"遍历"呢:对学过一些开发语言的朋友来说应该知道&…...
