分布形态的度量_峰度系数的探讨
集中趋势和离散程度是数据分布的两个重要特征,但要全面了解数据分布的特点,还应掌握数据分布的形态。
描述数据分布形态的度量有偏度系数和峰度系数,
其中偏度系数描述数据的对称性,峰度系数描述与正态分布的偏离程度。
峰度系数反映分布峰的尖峭程度的重要指标.
当峰度系数大于0时,两侧极端数据较多;
当峰度系数小于0时,两侧极端数据较少。
基本条件
*时间T固定,空间S固定
情况1:只改变中枢的T长短
np15a = np.concatenate((np.arange(0.5, 21, 1.5), np.full((12,), 20), np.arange(20, 40, 1.5)), axis=0)
np20a = np.concatenate((np.arange(0, 21, 2), np.full((18,), 20), np.arange(20, 41, 2)), axis=0)
np25a = np.concatenate((np.arange(0, 21, 2.5), np.full((22,), 20), np.arange(20, 41, 2.5)), axis=0)

峰度分别为①-0.34;②0.42;③1.22
结论:
①中枢越长,峰度系数越大。
情况2:只改变中枢的位置

峰度分别为:
0 -1.16
1 -0.84
2 -0.61[绿色]
3 -0.77
4 -1.1
结论:
①中枢越靠近均值(偏度接近0),峰值越大(-0.61);
②偏度的正负,对峰度没有影响。但偏度的绝对值越大,峰度值越小。
情况3:峰度值为0的abc浪
import numpy as np
from scipy.stats import kurtosis
def skew0(x1, x2, y=500, s=1):np00 = np.concatenate((np.arange(y-x2*s, y, s), np.full((x1,), y), np.arange(y+s, y+s+x2*s, s)), axis=0)npp = np.empty((0, len(np00)))npp = np.vstack((npp, np00))kt = kurtosis(npp[0])return kt, nppf12 = np.arange(100, 1000, 1)
for i in f12:for j in f12:kt, npp = skew0(i, j, 500, 1)if abs(kt) < 0.0001:print(i, j, i/j, j/i, kt)
结论
①a+c浪 / b浪的时间比值,约等于2.6712;
也就是说a浪和c浪匀速前提下,极限是2.67;
若a和c浪是水平,极限是8;
def skew0(x1, x2, y=500, s=10):np00 = np.concatenate((np.full((x2,), s), np.full((x1,), y), np.full((x2,), 2*y - s)), axis=0)npp = np.empty((0, len(np00)))npp = np.vstack((npp, np00))kt = kurtosis(npp[0])return kt, npp
相关文章:

分布形态的度量_峰度系数的探讨
集中趋势和离散程度是数据分布的两个重要特征,但要全面了解数据分布的特点,还应掌握数据分布的形态。 描述数据分布形态的度量有偏度系数和峰度系数, 其中偏度系数描述数据的对称性,峰度系数描述与正态分布的偏离程度。 峰度系数反映分布峰的尖峭程度的重要指标. 当…...
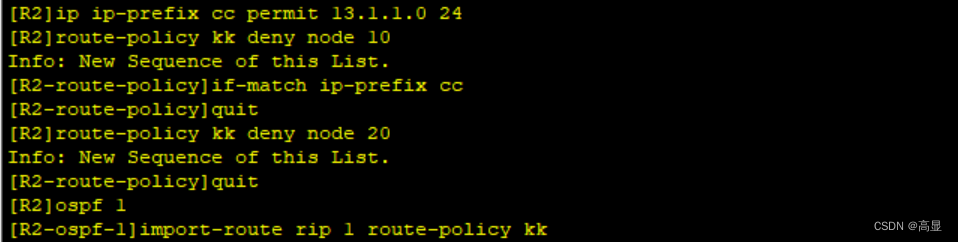
HCIP 重发布
拓扑图&IP划分如下: 第一步,配置接口IP&环回地址 以R1为例,R2~R4同理 interface GigabitEthernet 0/0/0 ip address 12.1.1.1 24 interface GigabitEthernet 0/0/1 ip address 13.1.1.1 24 interface LoopBack 0 ip address 1.1.1.…...

FX图中的节点代表什么操作
在 FX 图中,每个节点代表一个操作。这些操作可以是函数调用、方法调用、模块实例调用,也可以是 torch.nn.Module 实例的调用。每个节点都对应一个调用站点,如运算符、方法和模块。 一.节点操作 下面是一些节点可能代表的操作: 1…...

【Java 设计模式】创建型之单例模式
文章目录 1. 定义2. 应用场景3. 代码实现1)懒汉式2)饿汉式 4. 应用示例结语 在软件开发中,单例模式是一种常见的设计模式,它确保一个类只有一个实例,并提供一个全局访问点。单例模式在需要控制某些资源,如数…...
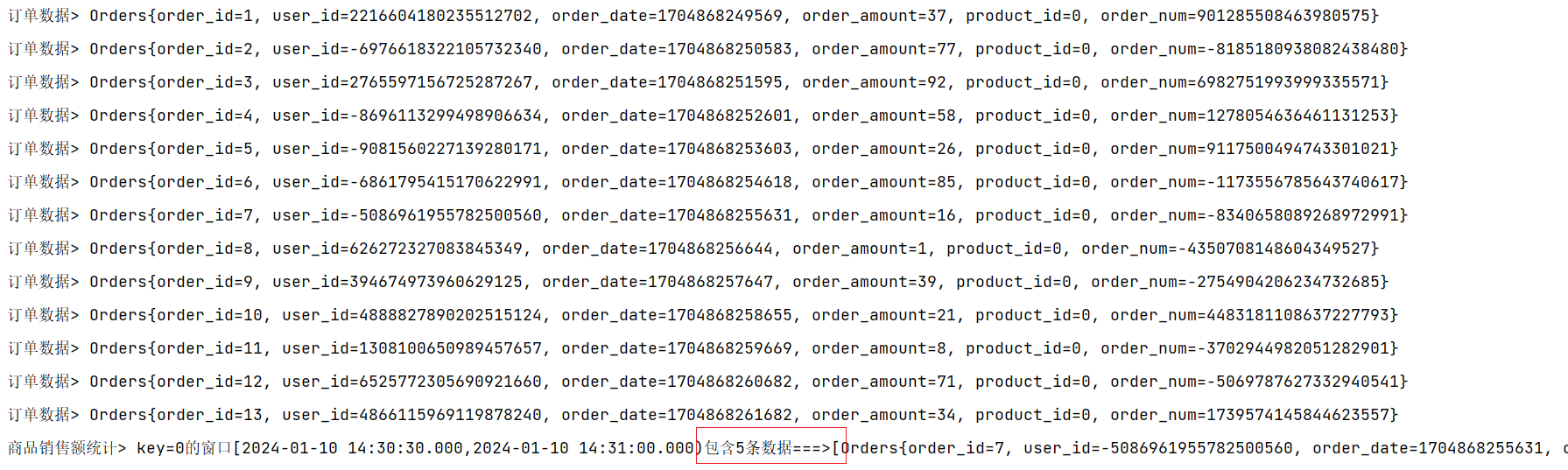
FlinkAPI开发之窗口(Window)
案例用到的测试数据请参考文章: Flink自定义Source模拟数据流 原文链接:https://blog.csdn.net/m0_52606060/article/details/135436048 窗口的概念 Flink是一种流式计算引擎,主要是来处理无界数据流的,数据源源不断、无穷无尽。…...
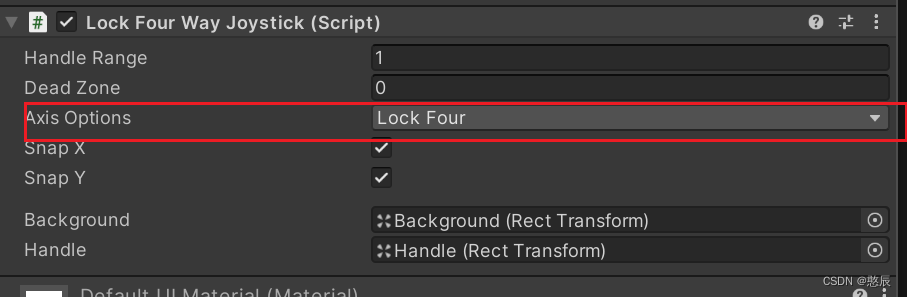
【Unity】Joystick Pack摇杆插件实现锁四向操作
Joystick Pack 简介:一款Unity摇杆插件,非常轻量化 摇杆移动类型:圆形、横向、竖向 摇杆类型: Joystick描述Fixed固定位置Floating浮动操纵杆从用户触碰的地方开始,一直固定到触碰被释放。Dynamic动态操纵…...

29 旋转工具箱
效果演示 实现了一个菜单按钮的动画效果,当鼠标悬停在菜单按钮上时,菜单按钮会旋转315度,菜单按钮旋转的同时,菜单按钮旋转的8个小圆圈也会依次旋转360度,并且每个小圆圈的旋转方向和菜单按钮的旋转方向相反࿰…...
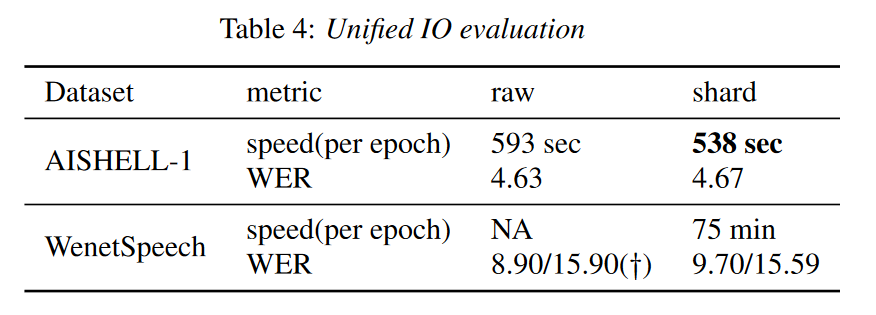
WeNet2.0:提高端到端ASR的生产力
摘要 最近,我们提供了 WeNet [1],这是一个面向生产(工业生产环境需求)的端到端语音识别工具包,在单个模型中,它引入了统一的两次two-pass (U2) 框架和内置运行时(built-in runtime)…...
)
第九部分 使用函数 (四)
目录 一、foreach 函数 二、if 函数 三、call 函数 一、foreach 函数 foreach 函数和别的函数非常的不一样。因为这个函数是用来做循环用的,Makefile 中的 foreach 函数几乎是仿照于 Unix 标准 Shell(/bin/sh)中的 for 语句,或…...
一文读懂「Prompt Engineering」提示词工程
在了解提示过程之前,先了解一下什么是提示prompt,见最后附录部分 一、什么是Prompt Engingering? 提示工程(Prompt Engingering),也被称为上下文提示(In-Context Prompting)&#x…...

微信小程序(一)简单的结构及样式演示
注释很详细,直接上代码 涉及内容: view和text标签的使用类的使用flex布局水平方向上均匀分布子元素垂直居中对齐子元素字体大小文字颜色底部边框的宽和颜色 源码: index.wxml <view class"navs"><text class"active…...

【设计模式】外观模式
前言 1. 单例模式(Singleton Pattern):保证一个类只有一个实例,并提供一个全局的访问点。 2. 工厂模式(Factory Pattern):定义一个创建对象的接口,但由子类决定要实例化的类是哪一…...
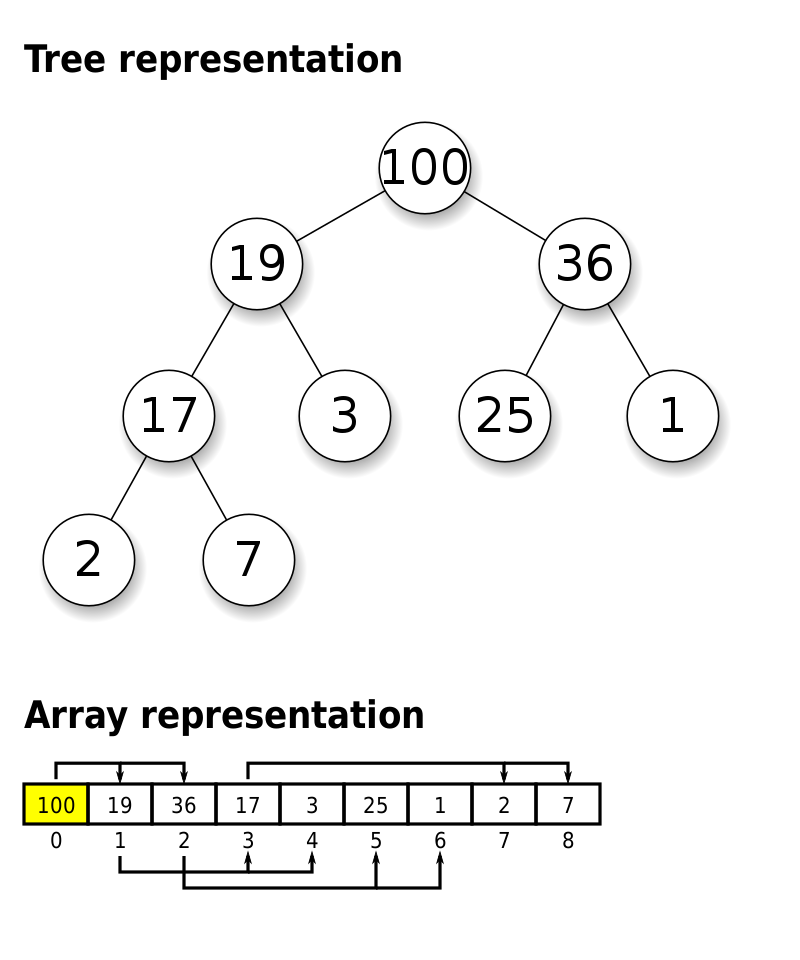
优先级队列(Priority Queue)
文章目录 优先级队列(Priority Queue)实现方式基于数组实现基于堆实现方法实现offer(E value)poll()peek()isEmpty()isFull() 优先级队列的实现细节 优先级队列(Priority Queue) 优先级队列是一种特殊的队列,其中的元素…...
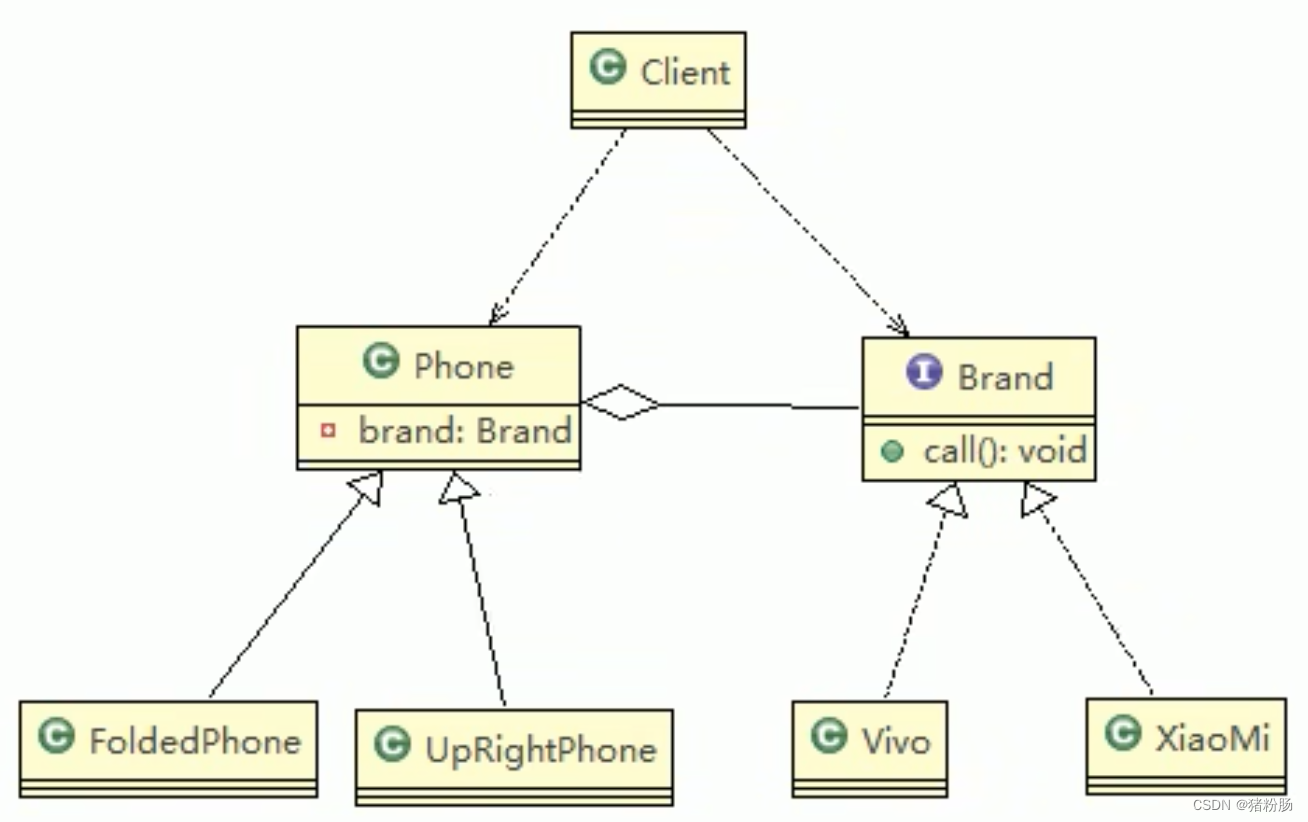
12-桥接模式(Bridge)
意图 将抽象部分与它的实现部分分离,使他们可以独立地变化 个人理解 一句话概括就是只要是在抽象类中聚合了某个接口或者抽象类,就是使用了桥接模式。 抽象类A中聚合了抽象类B(或者接口B),A的子类的方法中在相同的场…...

Zookeeper+Kafka概述
一 Zookeeper 1.1 Zookeeper定义 Zookeeper是一个开源的、分布式的,为分布式框架提供协调服务的Apache项目。 1.2 Zookeeper特点 Zookeeper:一个领导者(leader),多个跟随者(Follower)组成的…...
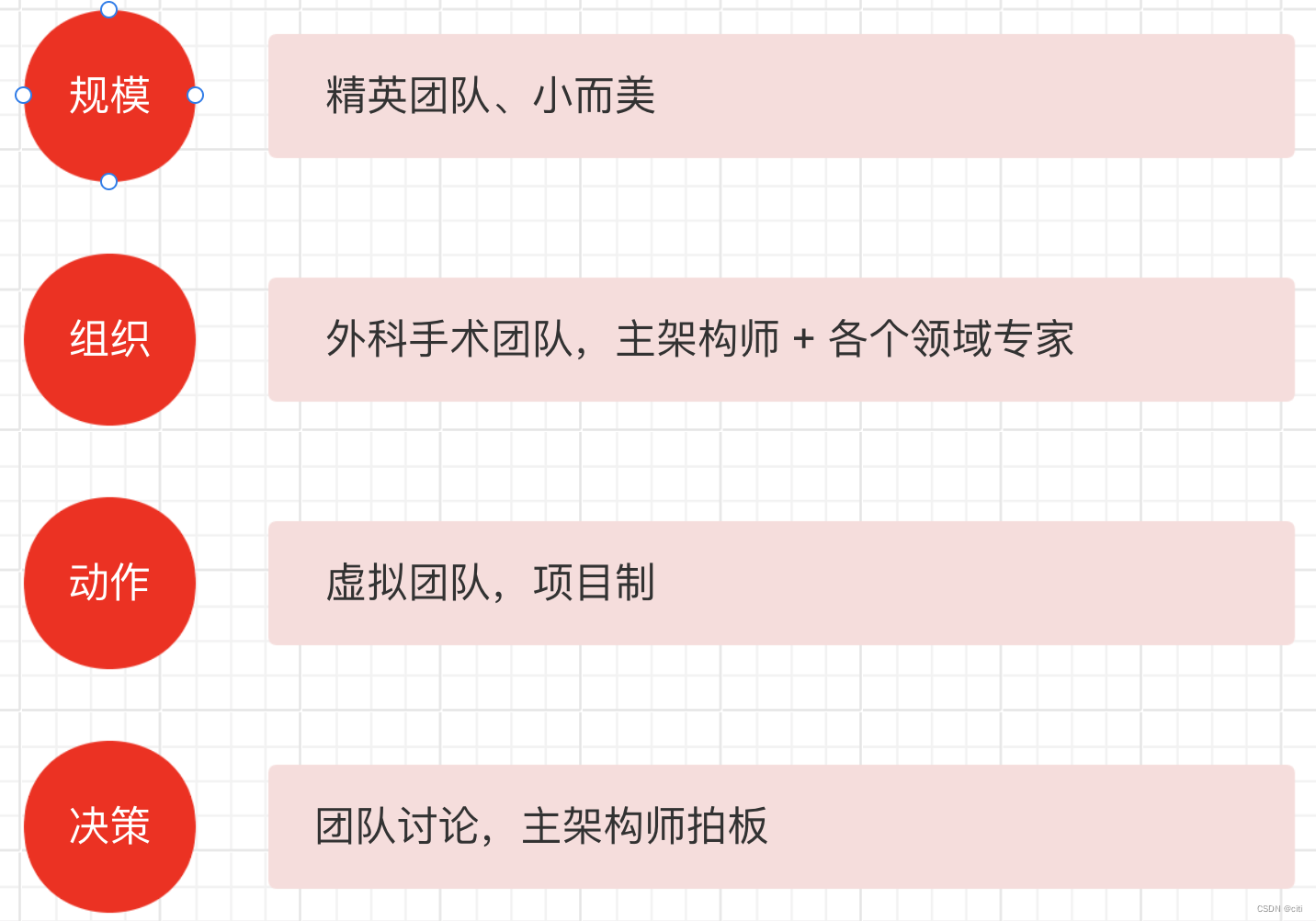
架构师 - 架构师是做什么的 - 学习总结
架构师核心定义 架构师是什么 架构师是业务和技术之间的桥梁 架构师的核心职责是消除不确定性、和降低复杂性 架构设计环 架构师的三个核心能力 架构师的三个关键思维 架构师主要职责 架构设计 Vs 方案设计 架构设计前期 主要任务 澄清不确定性 明确利益干系人的诉求消除冲…...
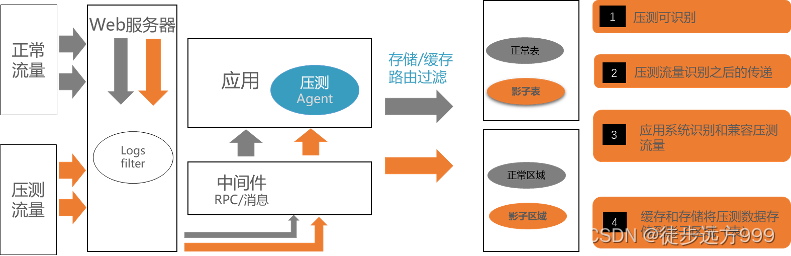
全链路压测方案(一)—方案调研
一、概述 在业务系统中,保证系统稳定至关重要,直接影响线上业务稳定和性能。测试工作作为保证生产质量的最后一关,扮演者重要的角色。全链路压测是一种重要的测试工具和手段。可以解决系统中多环节多节点无法全流程打满流量的痛点问题&a…...

c++关键字const
C中的const是一种常量修饰符。在变量、函数参数和成员函数中使用const可以限制其对数据的修改。 const修饰的数据在定义时必须进行初始化,且不能被修改,因此使用const可以提高代码的安全性和可读性。在C中,const修饰的成员函数表示该函数保证…...
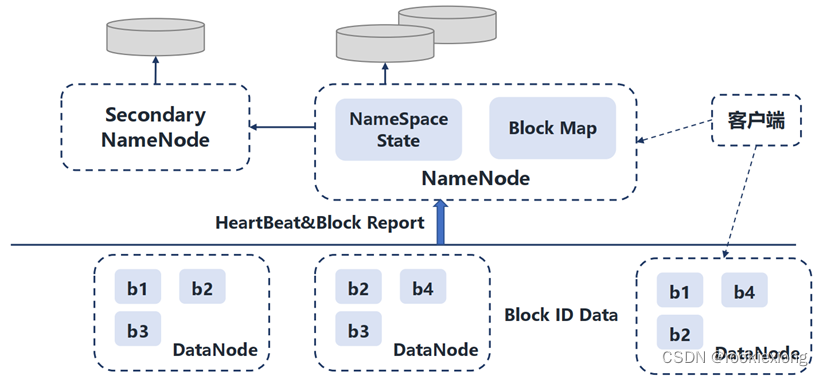
分布式计算平台 Hadoop 简介
Hadoop简介 Hadoop是一种分析和处理大数据的软件平台,是一个用Java语言实现的Apache的开源软件框架,在大量计算机组成的集群中实现了对海量数据的分布式计算。其主要采用MapReduce分布式计算框架,包括根据GFS原理开发的分布式文件系统HDFS、…...

系统学习Python——警告信息的控制模块warnings:常见函数-[warnings.warn]
分类目录:《系统学习Python》总目录 warnings.warn(message, categoryNone, stacklevel1, sourceNone, \*, skip_file_prefixesNone)常备用于引发警告、忽略或者触发异常。 如果给出category参数,则必须是警告类别类 ;默认为UserWarning。 或…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...
