优先级队列(Priority Queue)
文章目录
- 优先级队列(Priority Queue)
- 实现方式
- 基于数组实现
- 基于堆实现
- 方法实现
- offer(E value)
- poll()
- peek()
- isEmpty()
- isFull()
- 优先级队列的实现细节
优先级队列(Priority Queue)
优先级队列是一种特殊的队列,其中的元素不是按照进入队列的顺序出队,而是按照元素的优先级出队。在优先级队列中,元素的优先级最高的将会首先出队。
实现方式
基于数组实现
以下是基于数组的优先级队列的简单实现:
public class PriorityQueueArray<E extends Priority> {private E[] array;private int size = 0;public PriorityQueueArray(int capacity) {array = (E[]) new Object[capacity];}public boolean offer(E value) {if (size >= array.length) return false;int i = size - 1;while (i >= 0 && array[i].priority < value.priority) {array[i + 1] = array[i];i--;}array[i + 1] = value;size++;return true;}public E poll() {if (size == 0) return null;E result = array[size - 1];array[size - 1] = null;size--;return result;}public E peek() {if (size == 0) return null;return array[size - 1];}public boolean isEmpty() {return size == 0;}public boolean isFull() {return size == array.length;}
}
这个实现中,offer方法将元素插入到正确的位置以保持数组的有序性,poll方法删除并返回优先级最高的元素,peek方法返回但不删除优先级最高的元素。isEmpty和isFull方法分别用于检查队列是否为空或已满。
基于堆实现
基于数组的实现有一些缺点。例如,插入和删除元素可能需要移动大量的元素,特别是在最坏的情况下,这可能需要移动整个数组。因此,这种实现的时间复杂度可能会达到O(n),其中n是队列的大小。
这就是为什么在实践中,我们通常会使用更复杂的数据结构,如堆,来实现优先级队列。使用堆实现的优先级队列可以在O(log n)的时间复杂度内插入和删除元素,这比基于数组的实现更有效率。
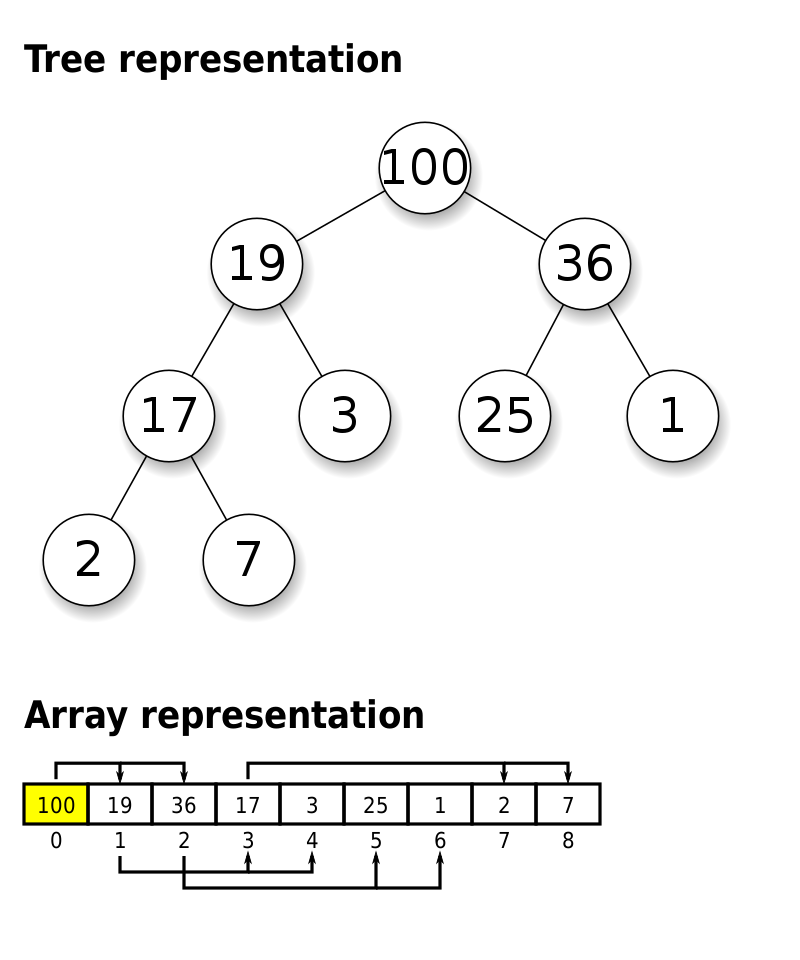
优先级队列通常使用堆(Heap)数据结构来实现。在Java中,可以通过实现Queue接口来创建一个优先级队列。下面的代码是一个使用最大堆实现的优先级队列:
public class PriorityQueue2<E extends Priority> implements Queue<E> {Priority[] array;public int size;public PriorityQueue2(int capacity) {array = new Priority[capacity];}...
}
这个优先级队列中的元素必须实现Priority接口,这个接口定义了元素的优先级。
方法实现
优先级队列通常包含以下方法:
offer(E value)
将元素插入到优先级队列中。如果队列已满,返回false;否则,将元素插入到正确的位置以保持堆的性质,并返回true。
@Override
public boolean offer(E value) {if(isFull())return false;if (size == 0){array[0] = value;}else{int child = size;int partent = (child - 1) / 2;while (child > 0 && value.priority > array[partent].priority){array[child] = array[partent];child = partent;partent = (child - 1) / 2;}array[child] = value;}size++;return true;
};
poll()
移除并返回优先级最高的元素。如果队列为空,返回null。
@Override
public E poll() {if (isEmpty())return null;E result = (E)array[0];array[0] = array[size-1];array[size] = null;size--;down(0);return result;
}private void down(int parent){int child1 = parent * 2 + 1;int child2 = parent * 2 + 2;if(child1 >= size )return;int maxIndex = child2 < size && array[child2].priority > array[child1].priority ? child2: child1;if(array[maxIndex].priority <= array[parent].priority)return;change(parent,maxIndex);down(maxIndex);
}private void change(int parent,int child){Priority p = array[parent];array[parent] = array[child];array[child] = p;
}
peek()
返回优先级最高的元素,但不移除它。如果队列为空,返回null。
@Override
public E peek() {if (isEmpty())return null;return (E)array[0];
}
isEmpty()
判断队列是否为空。
@Override
public boolean isEmpty() {return size == 0;
}
isFull()
判断队列是否已满。
@Override
public boolean isFull() {return size == array.length;
}
优先级队列的实现细节
优先级队列的实现主要基于一个堆结构。堆是一种特殊的完全二叉树,其中每个节点的值都大于或等于其子节点的值(最大堆)或小于或等于其子节点的值(最小堆)。
在我们的实现中,我们使用了一个数组array来存储堆的元素,并使用size来记录堆的大小。这是因为完全二叉树可以非常方便地用数组来表示。具体来说,对于数组中的任何一个元素,其左子节点的索引是2 * index + 1,右子节点的索引是2 * index + 2,而其父节点的索引是(index - 1) / 2。
相关文章:

优先级队列(Priority Queue)
文章目录 优先级队列(Priority Queue)实现方式基于数组实现基于堆实现方法实现offer(E value)poll()peek()isEmpty()isFull() 优先级队列的实现细节 优先级队列(Priority Queue) 优先级队列是一种特殊的队列,其中的元素…...
12-桥接模式(Bridge)
意图 将抽象部分与它的实现部分分离,使他们可以独立地变化 个人理解 一句话概括就是只要是在抽象类中聚合了某个接口或者抽象类,就是使用了桥接模式。 抽象类A中聚合了抽象类B(或者接口B),A的子类的方法中在相同的场…...

Zookeeper+Kafka概述
一 Zookeeper 1.1 Zookeeper定义 Zookeeper是一个开源的、分布式的,为分布式框架提供协调服务的Apache项目。 1.2 Zookeeper特点 Zookeeper:一个领导者(leader),多个跟随者(Follower)组成的…...
架构师 - 架构师是做什么的 - 学习总结
架构师核心定义 架构师是什么 架构师是业务和技术之间的桥梁 架构师的核心职责是消除不确定性、和降低复杂性 架构设计环 架构师的三个核心能力 架构师的三个关键思维 架构师主要职责 架构设计 Vs 方案设计 架构设计前期 主要任务 澄清不确定性 明确利益干系人的诉求消除冲…...
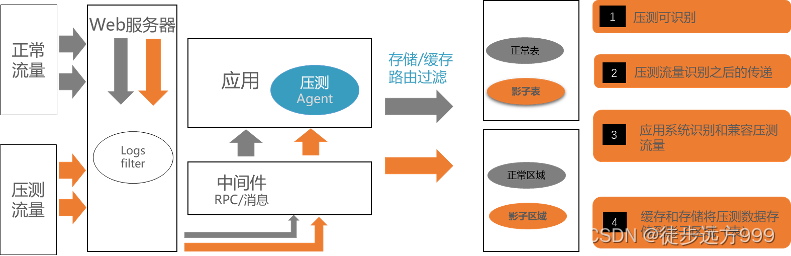
全链路压测方案(一)—方案调研
一、概述 在业务系统中,保证系统稳定至关重要,直接影响线上业务稳定和性能。测试工作作为保证生产质量的最后一关,扮演者重要的角色。全链路压测是一种重要的测试工具和手段。可以解决系统中多环节多节点无法全流程打满流量的痛点问题&a…...

c++关键字const
C中的const是一种常量修饰符。在变量、函数参数和成员函数中使用const可以限制其对数据的修改。 const修饰的数据在定义时必须进行初始化,且不能被修改,因此使用const可以提高代码的安全性和可读性。在C中,const修饰的成员函数表示该函数保证…...
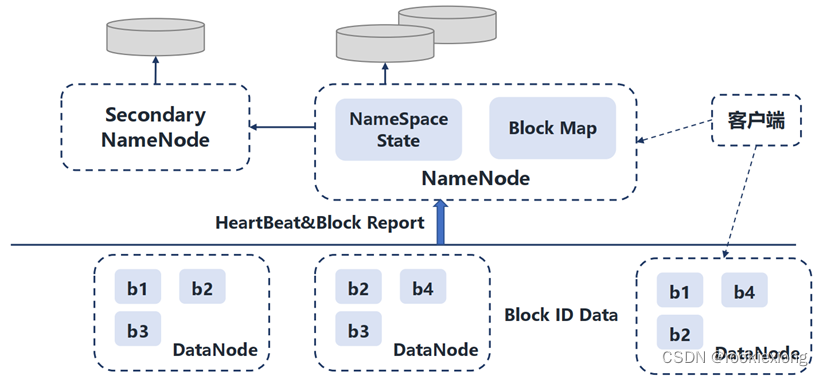
分布式计算平台 Hadoop 简介
Hadoop简介 Hadoop是一种分析和处理大数据的软件平台,是一个用Java语言实现的Apache的开源软件框架,在大量计算机组成的集群中实现了对海量数据的分布式计算。其主要采用MapReduce分布式计算框架,包括根据GFS原理开发的分布式文件系统HDFS、…...

系统学习Python——警告信息的控制模块warnings:常见函数-[warnings.warn]
分类目录:《系统学习Python》总目录 warnings.warn(message, categoryNone, stacklevel1, sourceNone, \*, skip_file_prefixesNone)常备用于引发警告、忽略或者触发异常。 如果给出category参数,则必须是警告类别类 ;默认为UserWarning。 或…...

监听键盘事件vue3封装hooks
监听页面键盘事件,执行对应方法 使用第三方API:vueuse 我封装的: 1. useKeyboardEvent.ts import { useMagicKeys } from vueuse/coreexport function enterKey(f: Function) {const { enter } useMagicKeys()watch(enter, v > {if (…...

Java Stream简化代码
使用原始流以获得更好的性能 使用 int、long 和 double 等基本类型时,请使用IntStream、LongStream 和 DoubleStream 等基本流,而不是 Integer、Long 和 Double 等装箱类型流。原始流可以通过避免装箱和拆箱的成本来提供更好的性能。 var array new i…...
py爬虫入门笔记(request.get的使用)
文章目录 Day11. 了解浏览器开发者工具2. Get请求http://baidu.com3. Post请求https://fanyi.baidu.com/sug4. 肯德基小作业 Day21. 正则表达式2. 使用re模块3. 爬取豆瓣电影Top250的第一页4. 爬取豆瓣电影Top250所有的250部电影信息 Day31. xpath的使用2. 认识下载照片线程池的…...

openssl3.2 - 官方demo学习 - encode - rsa_encode.c
文章目录 openssl3.2 - 官方demo学习 - encode - rsa_encode.c概述笔记END openssl3.2 - 官方demo学习 - encode - rsa_encode.c 概述 命令行参数 server_priv_key.pem client_priv_key.pem 这2个证书是前面certs目录里面做的 官方这个程序有bug, 给出2个证书, 还要从屏幕上输…...
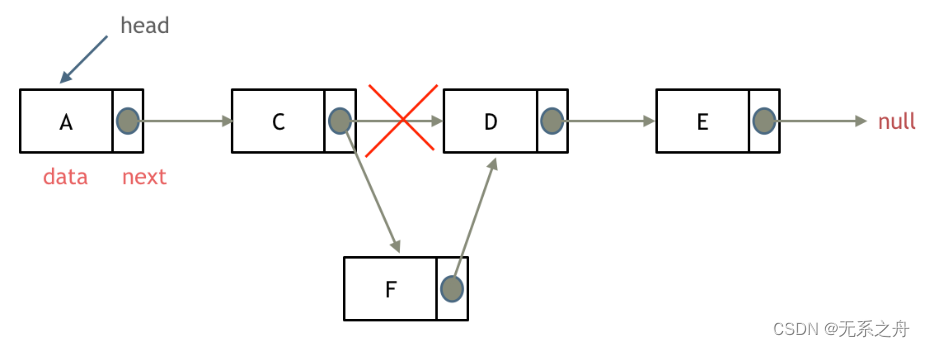
Day03
今日任务 链表理论基础203.移除链表元素707.设计链表206.反转链表 链表理论基础 1)单链表 单链表中的指针域只能指向节点的下一个节点 2)双链表 双链表:每一个节点有两个指针域,一个指向下一个节点,一个指向上一个…...

adb 常用命令汇总
目录 adb 常用命令 1、显示已连接的设备列表 2、进入设备 3、安装 APK 文件到设备 4、卸载指定包名的应用 5、从设备中复制文件到本地 6、将本地文件复制到设备 7、查看设备日志信息 8、重启设备 9、截取设备屏幕截图 10、屏幕分辨率 11、屏幕密度 12、显示设备的…...
ubuntu 2022.04 安装vcs2018和verdi2018
主要参考网站朋友们的作业。 安装时参考: ubuntu18.04安装vcs、verdi2018_ubuntu安装vcs-CSDN博客https://blog.csdn.net/qq_24287711/article/details/130017583 编译时参考: 【ASIC】VCS报Error-[VCS_COM_UNE] Cannot find VCS compiler解决方法_e…...

品牌推广与情绪价值的深度结合:市场大局下的新趋势与“准”原则
随着社会经济的快速发展和消费者心理的复杂化,品牌推广已经不再是单一的信息传递,而是一个与消费者建立情感连接、传达品牌价值的过程。在这个过程中,情绪价值起到了至关重要的作用。它不仅影响着消费者的购买决策,更是品牌与消费…...

React16源码: React中的不同的expirationTime的源码实现
不同的 expirationTime 1 )概述 在React中不仅仅有异步任务大部分情况下都是同步的任务,所以会有不同 expirationTime 的存在 2 )种类 A. Sync 模式,优先级最高 任务创建完成之后,立马更新到真正的dom里面是一个创建…...
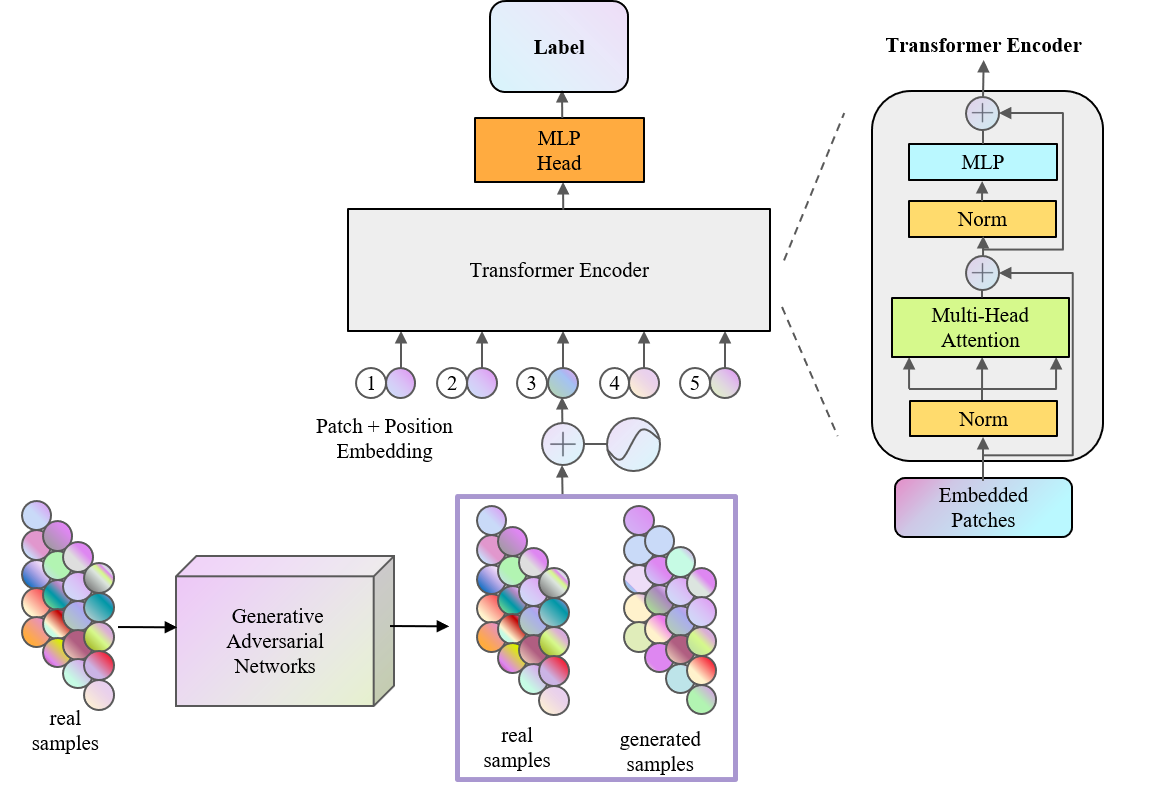
TRB 2024论文分享:基于生成对抗网络和Transformer模型的交通事件检测混合模型
TRB(Transportation Research Board,美国交通研究委员会,简称TRB)会议是交通研究领域知名度最高学术会议之一,近年来的参会人数已经超过了2万名,是参与人数和国家最多的学术盛会。TRB会议几乎涵盖了交通领域…...

Golang 打包
构建/打包 使用 Go 的构建命令: go build在包含 main 函数的包的目录下执行,它会生成一个可执行文件。文件名默认与包所在的目录名相同,但也可以使用 -o 选项来指定输出的文件名 交叉编译 Windows 环境下进行交叉编译以构建其他平台的可执…...

力扣每日一练(24-1-14)
做过类似的题,一眼就是双指针,刚好也就是题解。 if not nums:return 0p1 0 for p2 in range(1, len(nums)):if nums[p2] ! nums[p1]:p1 1nums[p1] nums[p2]return p1 1 根据规律,重复的数字必定相连,那么只要下一个数字与上一…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...
