RH850P1X芯片学习笔记-Flash Memory
文章目录
- Features
- Clock Supply
- Block Diagram
- Flash Size
- Memory Configuration
- Registers
- Register Base Address
- List of Registers
- Register Reset Condition
- 与Flash Memory相关的操作模式
- Functional Overview
- Option Bytes
- OPBT0 — Option Byte 0
- OPBT1 — Option Byte 1
- OPBT2 — Option Byte 2
- OPBT13 — Option Byte 13
- OPBT14 — Option Byte 14
- OPBT15 — Option Byte 15
Features
•代码flash容量:高达10兆字节的用户区域
编程方法:
- 通过串行接口与专用闪存编程器通信编程(串行编程)。
- 用户程序编程Flash(自编程)。
支持安全功能,以防止非法篡改或读取闪存中的数据。
支持保护功能,防止flash错误覆盖。
在Code Flash上支持OTP(一次性编程)
支持检测和纠正闪存中的错误。
支持BGO(后台操作)功能
- Code flash可以读取,而data flash正在编程。
- 当一个bank的flash被擦除/编程/读取时,另一个bank的flash可以被擦除/编程/读取。
Option Bytes寄存器值(设备的某些设置)可以在flash的扩展区域中配置
Code Flash上的最小可写单元是256bytes,Data Flash上的最小可写单元是4bytes
最小的可擦除单位是块。在Code Flash上8 kb或32 kb,在数据Flash上64bytes。
Clock Supply
下表列出了Flash控制逻辑(FACI)的时钟供应。

Block Diagram

Flash Size

Memory Configuration
RH850/P1x-C代码闪存中的用户区分为8kbytes或32kbytes块,可单独擦除
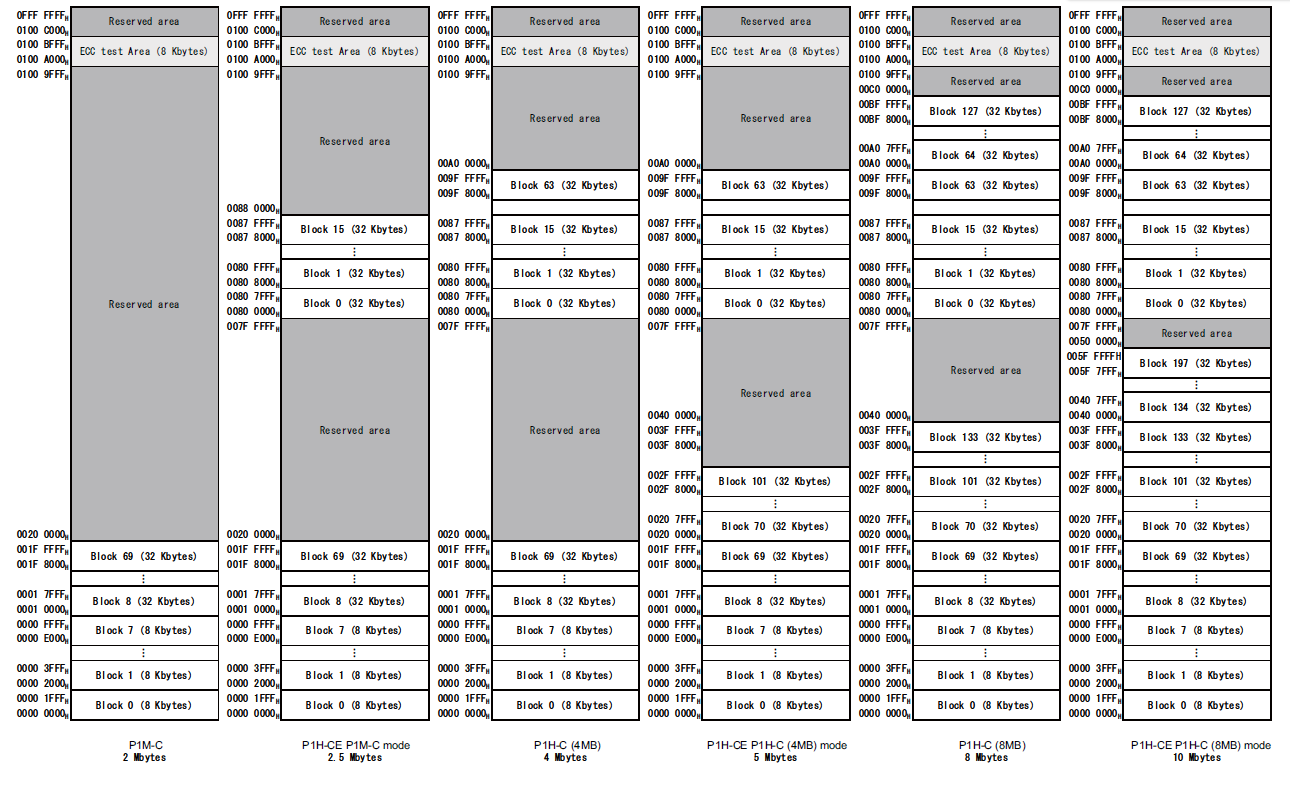

RH850/P1x-C数据闪存中的数据区被划分为64字节的块,可以单独擦除。
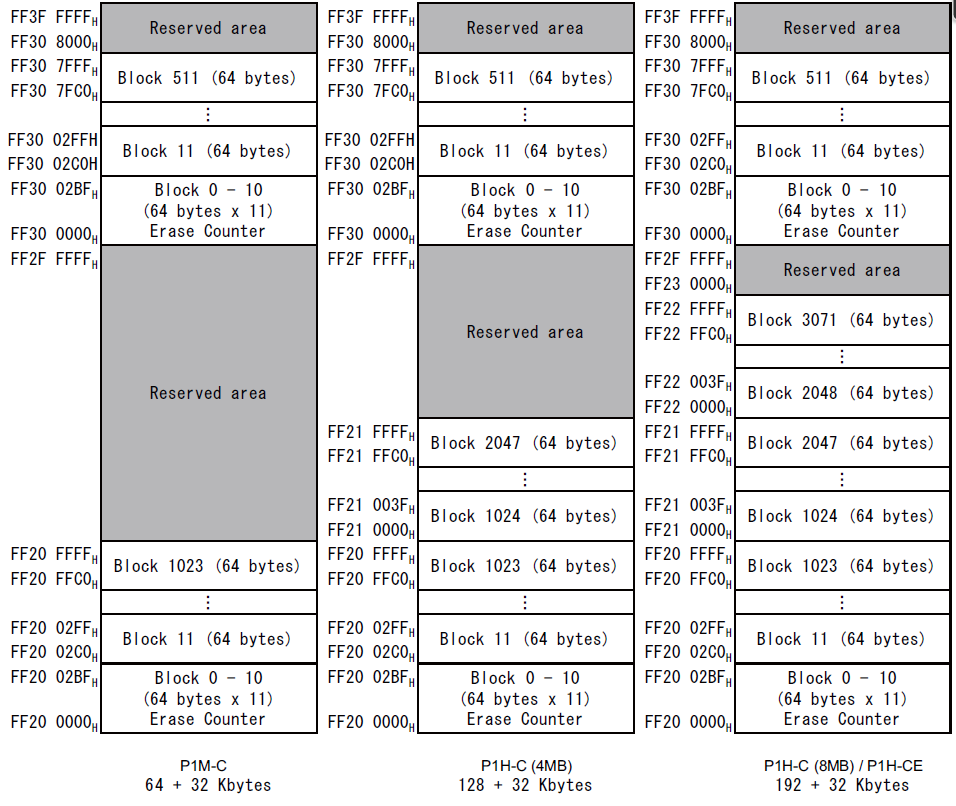
Registers
Register Base Address

List of Registers

Register Reset Condition
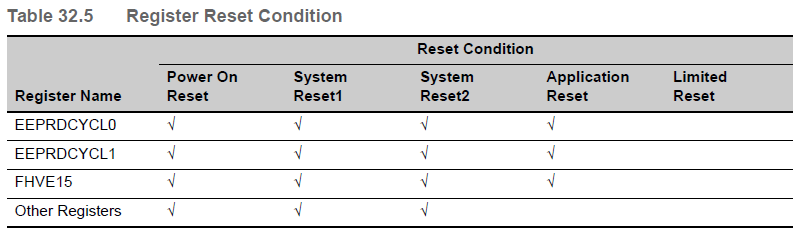
与Flash Memory相关的操作模式
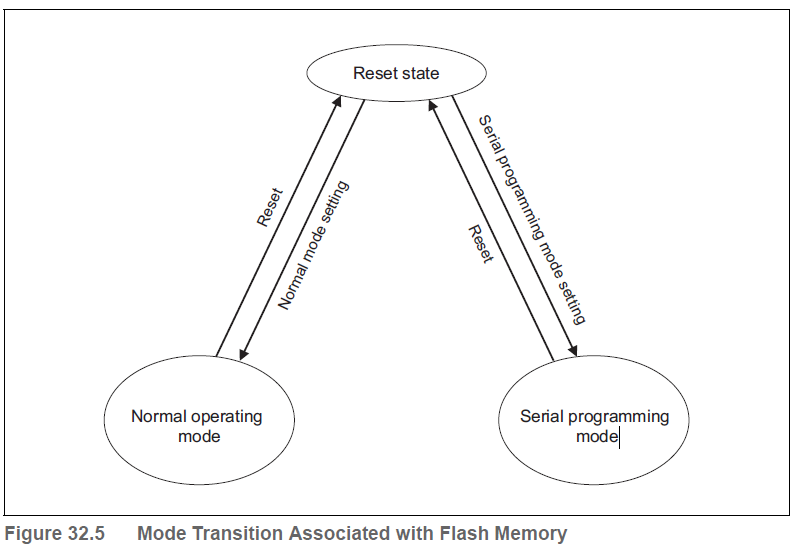
可编程和可擦除的flash区域以及复位后的启动程序取决于所选模式。模式之间的差异如表32.6所示

Functional Overview
RH850/P1x-C的片上闪存可以在安装到目标系统之前和之后进行编程,其编程功能采用专用的闪存编程器(串行编程)。
此外,还支持禁止在片上闪存中编写用户程序的安全功能,以防止程序被外部人员伪造
使用用户程序的编程功能(自编程)是适用于预期在目标系统的生产或装运之后修改程序的应用的方法。还支持对闪存区域进行安全编程的保护功能。
此外,通过在自编程期间利用对中断处理的支持,可以在各种条件下进行编程,例如与外部通信并行。
表32.7概述了编程方法和相应的操作模式。
Option Bytes
flash memory具有扩展区域(可选字节)来存储用户为各种目的指定的数据。设置的更改,例如使用选项字节的外设功能的初始设置,在从复位状态释放后生效。
OPBT0 — Option Byte 0

OPWDRUN0:该位启用或禁用WDTA0的自动启动。
0:禁用WDTA0自动启动。
1:启用WDTA0自动启动
OPWDOFV2 to OPWDOFV0:这些位选择WDTA0、WDTA1的溢出时间
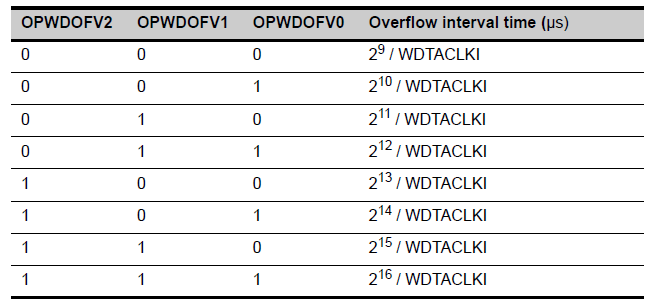
OPWD0MD:该位选择WDTA0、WDTA1的模式
0:慢速模式(WDTACLKI = 1/32 of CLK_IOSC)
1:快速模式(WDTACLKI = CLK_IOSC的1/1)
OPWDVAC:选择WDTA0、WDTA1变量启动代码)
该位指定触发寄存器,用于生成计数器重启触发器以避免计数器溢出。
0: WDTAnWDTE(固定)
1: WDTAnEVAC(变量)
注意:有关WDTA启动选项的详细信息,请参见第23节,窗口看门狗定时器A (WDTA)。
OPWDRUN1:该位启用或禁用WDTA1的自动启动(P1M-C除外)。
[p1h-c (4mb), p1h-c (8mb), p1h-ce]
0:关闭WDTA1自动启动。
1:启用WDTA1自动启动。
(P1M-C)
1:写值必须为1。
ETHDISABLE:以太网控制
0:表示以太网模块未启用。
1:以太网模块使能。
OPAUDR:选择AUD RAM监视器启用/禁用(仅限P1H-CE)
(P1H-CE)
0:禁用AUDR
1:启用AUDR
[P1M-C, P1H-C]
1:写值必须为1。
OPBT1 — Option Byte 1
OPBT1与时钟频率相关,如下图所示

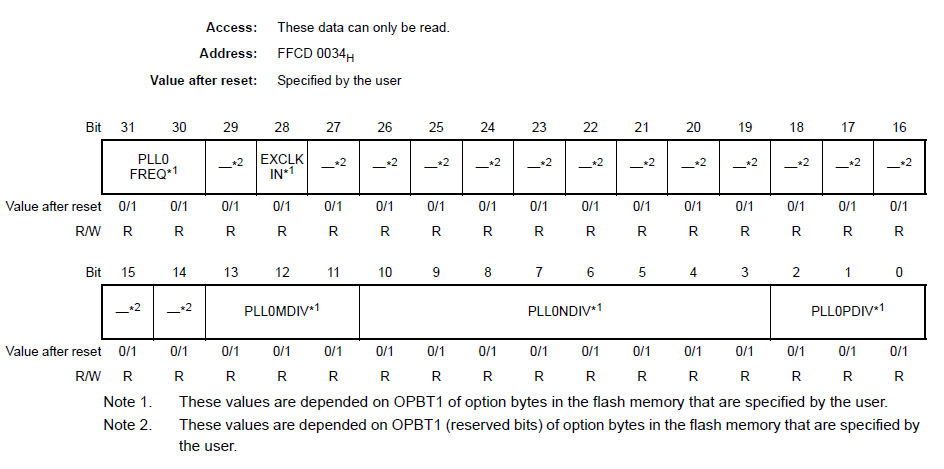
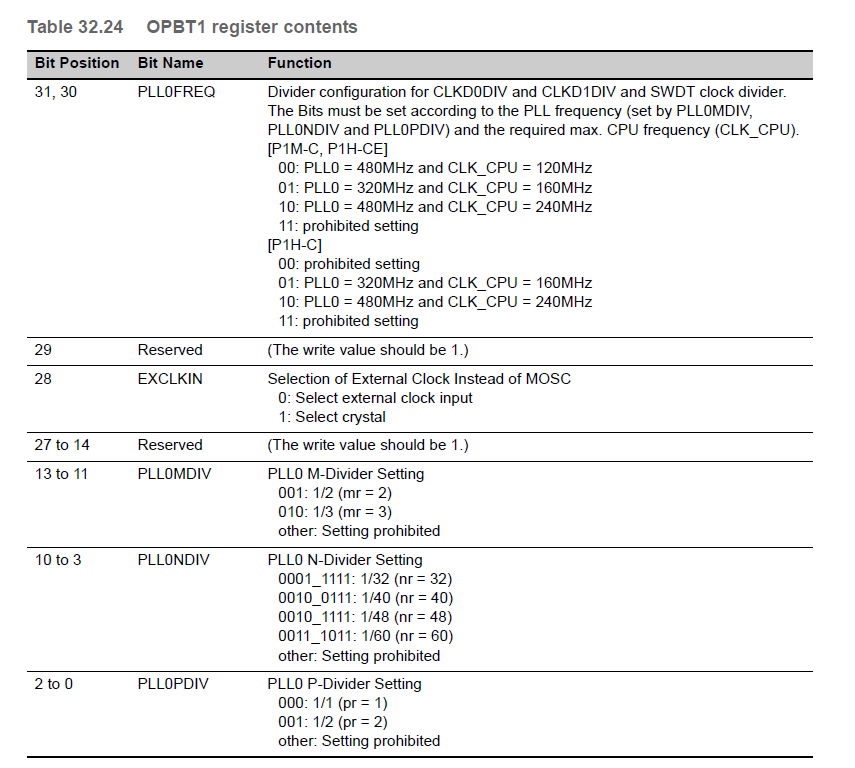
PLL0FREQ:CLKD0DIV和CLKD1DIV的分频器配置以及SWDT时钟分频器。
位必须根据锁相环频率设置(由PLL0MDIVPLL0NDIV和PLL0PDIV设置)和所需的最大值。CPU频率(CLK_CPU)。
[P1M-C, P1H-CE]
00: PLL0 = 480MHz, CLK_CPU = 120MHz
01: PLL0 = 320MHz, CLK_CPU = 160MHz
10: PLL0 = 480MHz, CLK_CPU = 240MHz
11:禁止设置
(P1H-C)
00:禁止设置
01: PLL0 = 320MHz, CLK_CPU = 160MHz
10: PLL0 = 480MHz, CLK_CPU = 240MHz
11:禁止设置
一般设置为10b,即PLL0设置为480MHz,CLK_CPU设置为240MHz
EXCLKIN:选择外部时钟代替MOSC
0:选择外部时钟输入
1:选择晶振
一般设置为1
PLL0MDIV:PLL0 m分压器设置
001: 1/2 (mr = 2)
010: 1/3 (mr = 3)
other:禁止设置
一般设置为001
PLL0NDIV:PLL0 n分频器设置
0001_1111: 1/32 (nr = 32)
0010_0111: 1/40 (nr = 40)
0010_1111: 1/48 (nr = 48)
0011_1011: 1/60 (nr = 60)
other:禁止设置
一般设置为0011_1011
PLL0PDIV:PLL0 P分频器设置
000: 1/1 (pr = 1)
001: 1/2 (pr = 2)
other:禁止设置
一般设置为0
OPBT2 — Option Byte 2
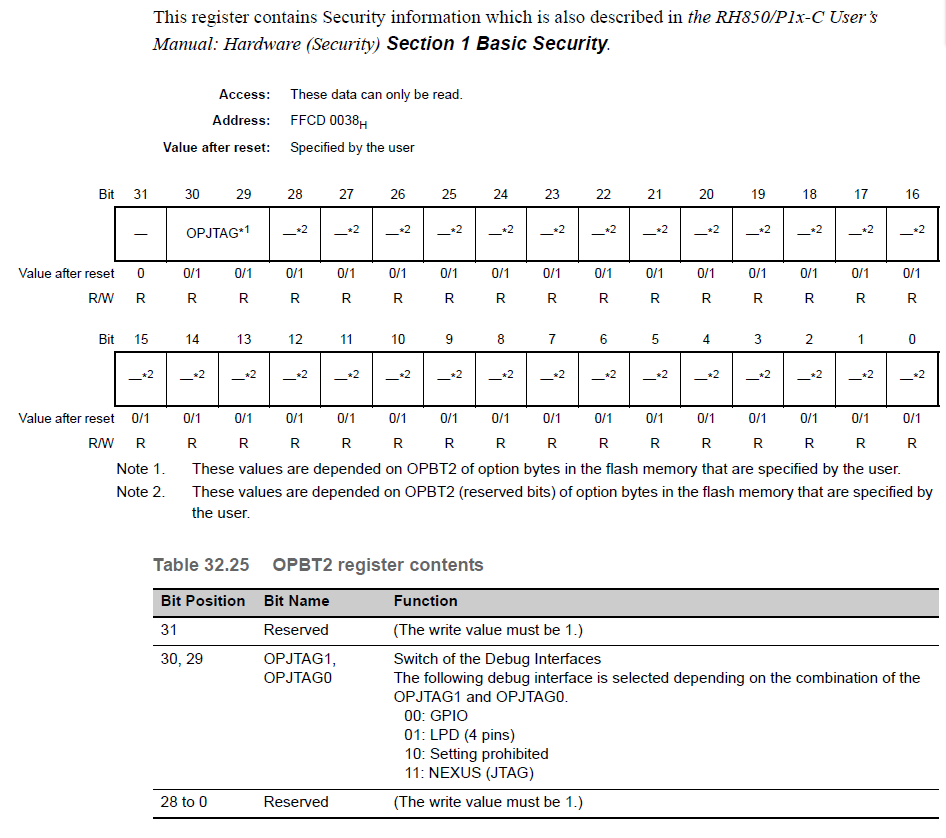
OPJTAG1,OPJTAG0:选择调试接口
OPBT13 — Option Byte 13
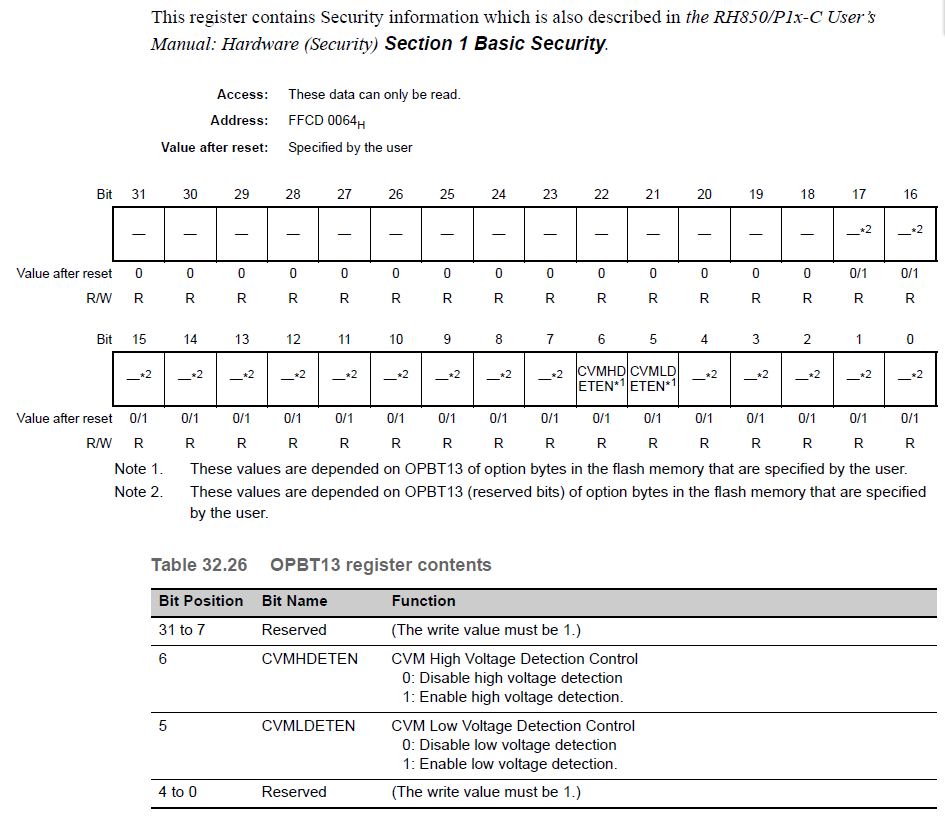
CVMHDETEN:CVM过压检测控制,1使能
CVMLDETEN:CVM欠压检测控制,1使能
OPBT14 — Option Byte 14

EMF:仿真模式选择,只有P1H-CE可以用,P1M-C,P1H-C都需要写1
PE2PB:PE2校验位是否启用,1启用

RD_SEL:阻尼电阻配置
PE2DIS:是否使能PE2,0使能

STARTUPPE:选择Start up PE使能控制
OPBT15 — Option Byte 15

CAP_SEL:主OSC电容配置
AMP_SEL:主OSC AMP配置
相关文章:

RH850P1X芯片学习笔记-Flash Memory
文章目录 FeaturesClock Supply Block DiagramFlash SizeMemory ConfigurationRegistersRegister Base AddressList of RegistersRegister Reset Condition 与Flash Memory相关的操作模式Functional OverviewOption BytesOPBT0 — Option Byte 0OPBT1 — Option Byte 1OPBT2 —…...
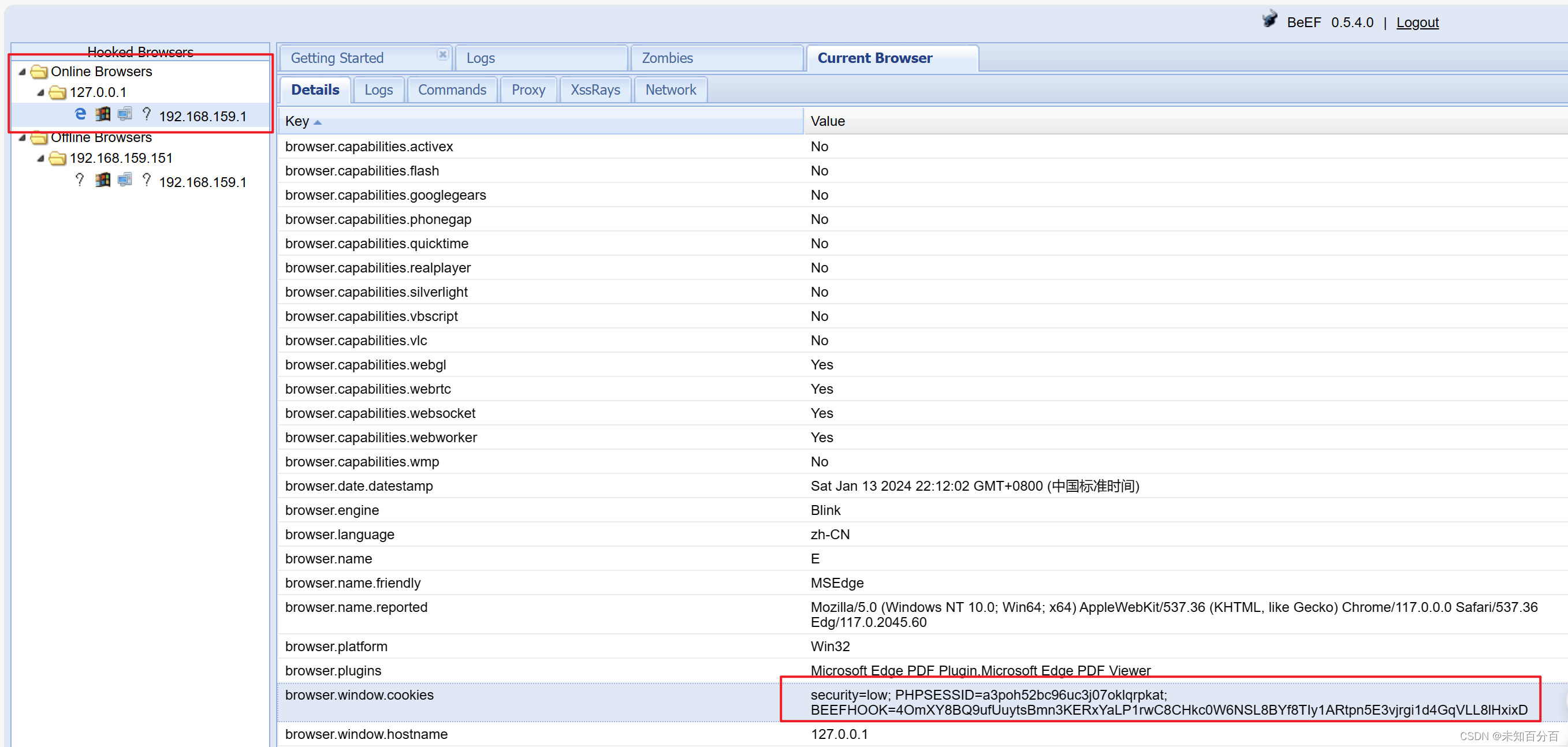
利用XSS漏洞打cookie
目录 1、为什么要打cookie? 2、怎样利用XSS来打cookie? 3、利用Bluelotus_xssReceiver平台来打cookie 4、利用beef-xss平台来打cookie 上一篇给大家介绍了xss漏洞的基础知识,在本篇章将会介绍和演示一下利用xss漏洞打cookie的演示&#x…...

用java写个redis工具类
下面是一个简单的Redis工具类的示例,使用Java语言编写: import redis.clients.jedis.Jedis;public class RedisUtils {private static Jedis jedis;public static void connect(String host, int port) {jedis new Jedis(host, port);}public static v…...

实现防抖函数
// 防抖就是,事件触发 delay 秒后再执行,如果有重新的触发,重新计时 function debounce(func, delay) {if(typeof func ! function) {return}let timer 0return function () {if (timer) {clearTimeout(timer)timer null}timer setTimeout…...

MetaGPT task1学习
基础知识学习了解: 安装环境: 获取MetaGPT 使用pip获取MetaGPT pip install -i https://pypi.tuna.tsinghua.edu.cn/simple metagpt0.5.2 配置MetaGPT 完成MetaGPT后,我们还需要完成一些配置才能开始使用这个强力的框架,包括配…...

关于量子计算机的设想
从CPU架构说起 CISCRISCNISCCCSC CISC是复杂指令集计算机,以x86为代表; RISC是精简指令集计算机,以ARM为代表; NISC是无指令集计算机,CCSC是核-电路分离计算机,这两个是本文要讨论的内容。 如果没有指令…...
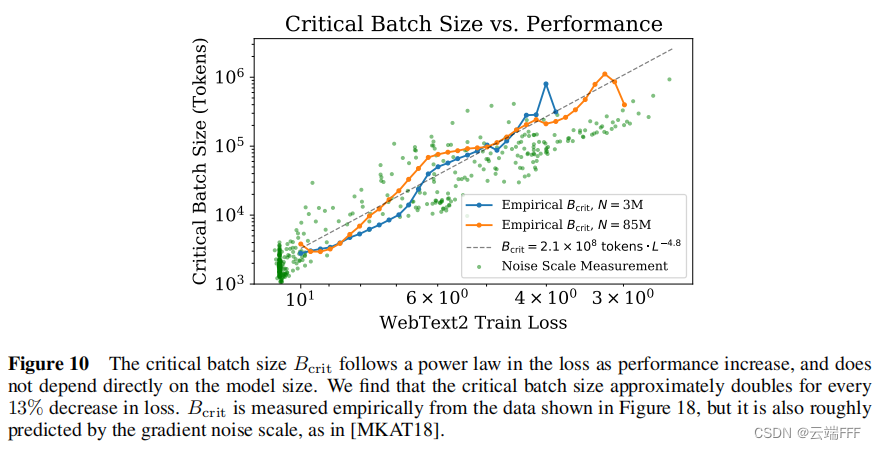
序列模型(4)—— Scaling Laws
本文介绍 LLM 训练过程中重要的 Scaling Laws,这是一个经验规律,指出了固定训练成本(总计算量FLOPs) C C C 时,如何调配模型规模(参数量) N N N 和训练 Token 数据量 D D D,才能实现…...
【软件测试学习笔记1】测试基础
1.软件测试的定义 软件的定义:控制计算机硬件工作的工具 软件的基本组成:页面客户端,代码服务器,数据服务器 软件产生的过程:需求产生(产品经理),需求文档,设计效果图…...

pytorch详细探索各种cnn卷积神经网络
目录 torch.nn.functional子模块详解 conv1d 用法和用途 使用技巧 适用领域 参数 注意事项 示例代码 conv2d 用法和用途 使用技巧 适用领域 参数 注意事项 示例代码 conv3d 用法和用途 使用技巧 适用领域 参数 注意事项 示例代码 conv_transpose1d 用法…...

OpenCV——八邻域断点检测
目录 一、理论基础1、八邻域2、断点检测 二、代码实现三、结果展示四、参考链接 OpenCV——八邻域断点检测由CSDN点云侠原创,爬虫自重。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 一、理论基础 1、八邻域 图1 八邻域示意图 图…...

leetcode238:除自身以外数组的乘积
文章目录 1.使用除法(违背题意)2.左右乘积列表3.空间复杂度为O(1)的方法 在leetcode上刷到了这一题,一开始并没有想到好的解题思路,写篇博客再来梳理一下吧。 题目要求: 不使用除法在O(n)时间复杂度内 1.使用除法&am…...
VTK开发调试环境下载(VTK开发环境一步到位直接开发,无需自己配置编译 VS2017+Qt5.12.10+VTK)
一、无与伦比的优势 直接下载代码就可以调试的VTK代码仓库。 二、资源制作原理 这个资源根据VTK源码 编译出动态库文件 pdb lib dll 文件( x64 debug ) 并将这两者同时放在一个代码仓库里,下载就能用。 三、使用方法(vtk-so…...

【JAVA】在 Queue 中 poll()和 remove()有什么区别
🍎个人博客:个人主页 🏆个人专栏:JAVA ⛳️ 功不唐捐,玉汝于成 目录 前言 正文 poll() 方法: remove() 方法: 区别总结: 结语 我的其他博客 前言 在Java的Queue接口中&…...

常用Java代码-Java中的Optional类和null安全编程
在Java中,Optional 是一个可以为null的容器对象。如果值存在则isPresent()方法返回true。调用get()方法会返回值,如果值为null则抛出NullPointerException。以下是一个详细的代码详解。 在之前的Java版本中,程序员需要手动检查是否为null&am…...

android.os.NetworkOnMainThreadException
问题 android.os.NetworkOnMainThreadException详细问题 核心代码如下: import android.os.Bundle;import androidx.appcompat.app.AppCompatActivity;import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import ja…...

Java生成四位数随机验证码
引言: 我们生活中登录的时候都要输入验证码,这些验证码是为了增加注册或者登录难度,减少被人用脚本疯狂登录注册导致的一系列危害,减少数据库的一些压力。 毕竟那些用脚本生成的账号都是垃圾账号 本次实践:生成这样的…...
)
编程探秘:Python深渊之旅-----数据可视化(八)
客户提出了对数据报告和图表的具体要求,这使得团队需要快速掌握数据可视化的技巧。派超决定深入了解 Python 中的数据可视化工具。 派超(兴奋地):我们有机会做些真正酷炫的数据报告了!我听说 Python 有很棒的图表库。…...
上海亚商投顾:创业板指冲高回落 光伏、航运股逆势走强
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 一.市场情绪 沪指1月12日冲高回落,创业板指午后跌近1%。北证50指数跌超6%,倍益康、华信永道、众诚科…...

Python3 中常用字符串函数介绍
介绍 Python 中有几个与 字符串数据类型相关的内置函数。这些函数让我们能够轻松修改和操作字符串。我们可以将函数视为在代码元素上执行的操作。内置函数是在 Python 编程语言中定义的,并且可以随时供我们使用的函数。 在本教程中,我们将介绍在 Pytho…...

Python - 深夜数据结构与算法之 AVL 树 红黑树
目录 一.引言 二.高级树的简介 1.树 2.二叉树 3.二叉搜索树 4.平衡二叉树 三.AVL 树 ◆ 插入节点 ◆ 左旋 ◆ 右旋 ◆ 左右旋 ◆ 右左旋 ◆ 一般形式 ◆ 实际操作 ◆ 总结 四.红黑树 ◆ 概念 ◆ 示例 ◆ 对比 五.总结 一.引言 前面我们介绍了二叉树、二叉…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
