华为OD机试真题-围棋的气--Java-OD统一考试(C卷)
题目描述:
围棋棋盘由纵横各19条线垂直相交组成,棋盘上一共19x19=361个交点,对弈双方一方执白棋,一方执黑棋,落子时只能将棋子置于交点上。
“气”是围棋中很重要的一个概念,某个棋子有几口气,是指其上下左右方向四个相邻的交叉点中,有几个交叉点没有棋子,由此可知:
1、在棋盘的边缘上的棋子最多有3口气(黑1),在棋盘角点的棋子最多有2口气(黑2),其它情况最多有4口气(白1)
2、所有同色棋子的气之和叫作该色棋子的气,需要注意的是,同色棋子重合的气点,对于该颜色棋子来说,只能计算一次气,比如下图中,黑棋一共4口气,而不是5口气,因为黑1和黑2中间红色三角标出的气是两个黑棋共有的,对于黑棋整体来说只能算一个气。
3、本题目只计算气,对于眼也按气计算,如果您不清楚“眼”的概念,可忽略,按照前面描述的规则计算即可。
现在,请根据输入的黑棋和白棋的坐标位置,计算黑棋和白起一共各有多少气?
输入描述:
输入包括两行数据,如:
0 5 8 9 9 10
5 0 9 9 9 8
1、每行数据以空格分隔,数据个数是2的整数倍,每两个数是一组,代表棋子在棋盘上的坐标;
2
相关文章:
)
华为OD机试真题-围棋的气--Java-OD统一考试(C卷)
题目描述: 围棋棋盘由纵横各19条线垂直相交组成,棋盘上一共19x19=361个交点,对弈双方一方执白棋,一方执黑棋,落子时只能将棋子置于交点上。 “气”是围棋中很重要的一个概念,某个棋子有几口气,是指其上下左右方向四个相邻的交叉点中,有几个交叉点没有棋子,由此可知: …...

CANFD数据记录仪在新能源汽车复杂路测下的应用
CANFD数据记录仪在新能源汽车复杂路测下的应用 汽车制造商在生产预批量阶段的耐久性测试中,为了检测潜在故障,必须让车辆在严酷的路况和环境下接受测试。为确保能回溯故障发生的现场情况,我们需要对测试数据精准记录与储存。这些数据是新车型优化迭代的关键,也是确保产品质量的…...

java: 5-6 break
文章目录 1. break1.1 介绍1.2 语法和流程图1.3 入门练习1.4 细节说明1.5 练习 【老韩视频p137-】 1. break 看个需求:随机生成 1-100 的一个数,直到生成了 97 这个数,看看你一共用了几次? 【思路分析:循环,但是循环的次数不知道…...
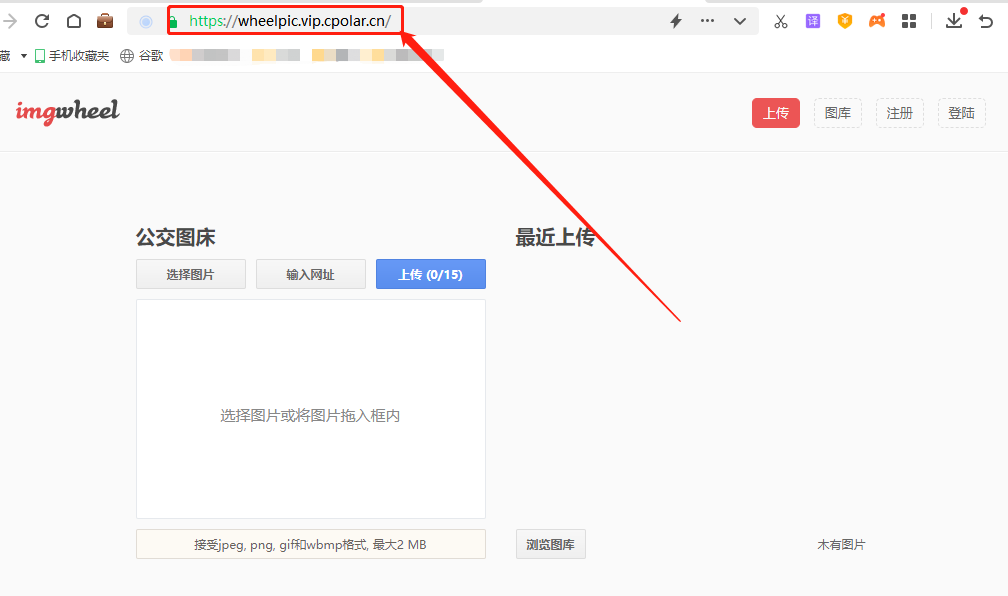
如何使用Imagewheel搭建一个简单的的私人图床无公网ip也能访问
文章目录 1.前言2. Imagewheel网站搭建2.1. Imagewheel下载和安装2.2. Imagewheel网页测试2.3.cpolar的安装和注册 3.本地网页发布3.1.Cpolar临时数据隧道3.2.Cpolar稳定隧道(云端设置)3.3.Cpolar稳定隧道(本地设置) 4.公网访问测…...
)
响应式编程Reactor API大全(上)
Reactor 是一个基于响应式编程的库,主要用于构建异步和事件驱动的应用程序。Reactor 提供了丰富的 API,包括创建、转换、过滤、组合等操作符,用于处理异步数据流。以下是一些 Reactor 的主要 API 示例: pom依赖 <dependencyMan…...

vue3自定义指令
一个自定义指令由一个包含类似组件生命周期钩子的对象来定义。钩子函数会接收到指令所绑定元素作为其参数。 页面内创建自定义指令 下面是一个自定义指令的例子,当一个 input 元素被 Vue 插入到 DOM 中后,它会被自动聚焦: <script setu…...
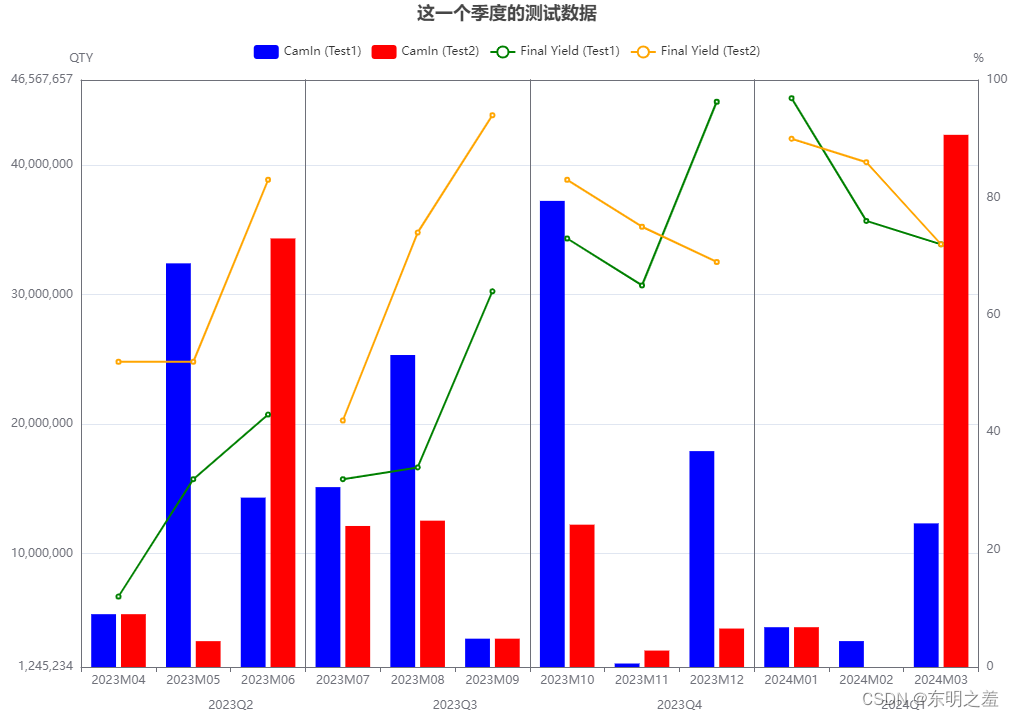
ECharts 多季度连续显示到一个图中。
效果图 二.相关option 以下option可以复制到 echarts的编辑器 进行查看修改 const site test1; const site2 test2;const qtrlyOption function (data: any, titleText: string): any {//获取最大值 。最大最小值的目的是:使左右里边的所有bar使用同一个指标let …...

【Microsoft Copilot】手机端发布 ——GPT-4, DALL-E3 免费用
Microsoft Copilot 关于Microsoft CopilotMicrosoft Copilot 的特点1. 可以在手机端使用:2. 可以免费使用GPT-4。3. 可以无限制地使用GPT-4。4. 可以使用DALL-E3生成图片。5. 搜索功能6. 图像识别 Microsoft Copilot的缺点和注意事项1. 非常容易报错2. 不支持长篇聊…...

[蓝桥杯 2013 省 AB] 错误票据
题目背景 某涉密单位下发了某种票据,并要在年终全部收回。 题目描述 每张票据有唯一的 ID 号,全年所有票据的 ID 号是连续的,但 ID 的开始数码是随机选定的。因为工作人员疏忽,在录入 ID 号的时候发生了一处错误,造…...
)
IDEA GitHub令牌原理(Personal Access Token)
1.IDEA的add github account 是什么原理? 在IntelliJ IDEA中添加GitHub账户,主要是为了让IDEA能够与GitHub进行交互,如克隆GitHub上的仓库,提交代码到GitHub等。其基本原理如下: 用户在IDEA中输入GitHub的用户名和密…...

[开发语言][python][c++]:C++中的this指针和Python中的Self -- 26岁生日
C中的this指针和Python中的Self 1. python中的Self2. C中的this指针3. C中的this指针和Python中self的异同点: 以朋友的新岁祝福开篇,祝笔者也祝大家☺️: 一岁一礼 一寸欢喜且喜且乐 且以永日 From VardoZ癸卯年十一月廿六(兔年)之…...

Android Traceview 定位卡顿问题
Traceview 是一个 Android 性能分析工具,用于时间性能分析,主要帮助开发者了解应用程序中各个方法的执行时间和调用关系。Traceview 可以通过图形化界面查看应用程序的代码执行细节,包括每个方法的调用次数、方法调用的时间消耗、方法调用堆栈…...
第三方 Cookie 被禁用?企业该如何实现用户精准运营和管理?
从 1 月 4 日开始,谷歌 Chrome 浏览器将逐步禁用第三方 Cookie 。作为全球最大的浏览器之一,Chrome 的这一动作无疑将引发行业内的重大变革。一直以来,第三方 Cookie 都是网络营销和广告的重要工具。然而,随着人们对隐私保护的日益…...
-基于ETAS软件)
Autosar PNC网络管理配置(2)-基于ETAS软件
文章目录 BswM初始化PNC对PDU的控制BswMModeRequestPortBswMModeConditionBswMLogicalExpressionBswMRuleBswMActionListEcuMEcuMWakeupSourceEcuMShutdownCauseEcuMRbAlSwitchOffCalloutEcuMRbOnGoOff...

【SpringMVC快速使用】1.@RestController @RequestMapping 2.logback的使用
背景:为何从这个最简单的 例子写起呢? 那是因为我们的管理后台之类的都是别人写的,我也听说了大家说:只用Post请求就足够了,但是却发现,在浏览器中测试时,默认是GET请求,如果直接写…...

C2593 operator << 不明确
错误 C2593 “operator <<” 不明确,通常出现在C代码中,当你尝试使用<<运算符(通常用于输出或位移运算)时,编译器无法确定使用哪个重载版本的运算符。这个错误可能由几个原因引起: 多个重载冲突…...

vue:使用【3.0】:条件模块
一、条件层级效果图 二、代码 <template><ContentWrap><!-- 添加条件分支:level1 --><div class"btnBox" v-if"isEdit"><el-button type"primary" click"add">添加条件分支</el-button></div…...

Kafka与RabbitMQ的区别
消息队列介绍 消息队列(Message Queue)是一种在分布式系统中进行异步通信的机制。它允许一个或多个生产者在发送消息时暂时将消息存储在队列中,然后由一个或多个消费者按顺序读取并处理这些消息。 消息队列具有以下特点: 异步通…...
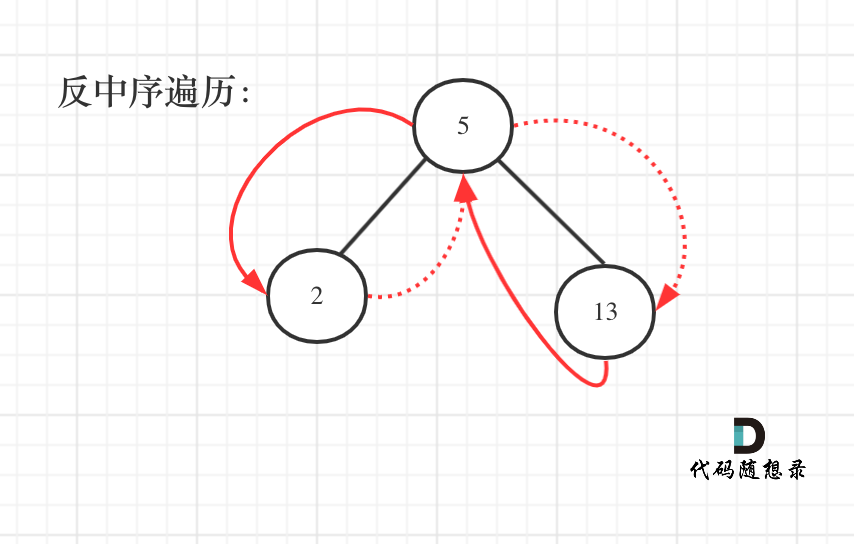
C++力扣题目538--把二叉搜索树转换为累加树
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。 提醒一下,二叉搜索树满足下列约束条件&#…...

曲线生成 | 图解贝塞尔曲线生成原理(附ROS C++/Python/Matlab仿真)
目录 0 专栏介绍1 贝塞尔曲线的应用2 图解贝塞尔曲线3 贝塞尔曲线的性质4 算法仿真4.1 ROS C仿真4.2 Python仿真4.3 Matlab仿真 0 专栏介绍 🔥附C/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...
