2024.1.11力扣每日一题——构造有效字符串的最少插入数
2024.1.11
- 题目来源
- 我的题解
- 方法一 暴力模拟
- 方法二 动态规划
- 方法三 直接拼接
- 方法四 计算组数
题目来源
力扣每日一题;题序:2645
我的题解
方法一 暴力模拟
直接模拟,根据题意可知 若是abc则不用插入,若是ab,ac,bc这需要 插入一个字符,其他的则需要插入两个字符。因此使用String的替换功能,先将word中的所有abc替换成 _ ,然后再分别将ab,ac,bc从左到右替换成 _ ,最后统计剩下的字符中 a b c的数量
时间复杂度:O( n 2 n^2 n2) n是字符串的长度。除了遍历的O(n),还有替换方法内部的O(n)
空间复杂度:O(1)
public int addMinimum(String word) {word=word.replaceAll("abc","_");int n=word.length();if(n==0)return 0;int res=0;while(word.contains("ab")){res++;word=word.replaceFirst("ab","_");}while(word.contains("bc")){res++;word=word.replaceFirst("bc","_");}while(word.contains("ac")){res++;word=word.replaceFirst("ac","_");}for(int i=0;i<word.length();i++){char ch=word.charAt(i);if(ch>='a'&&ch<='c'){res+=2;}}return res;
}
方法二 动态规划
定义dp[i]状态表示前i个字符凑成若干个abc所需插入的字符数,则转移过程:
- 若第i个字符单独在一组abc中,则dp[i]=dp[i-1]+2
- 若word[i]>word[i-1]则表示word[i]和word[i-1]在一组abc中,则dp[i]=dp[i-1]-1
时间复杂度:O(n)
空间复杂度:O(n)
public int addMinimum(String word) {int n=word.length();int[] dp=new int[n+1];for(int i=0;i<n;i++){dp[i+1]=dp[i]+2;if(i<n-1&&word.charAt(i+1)>word.charAt(i)){dp[i+1]=dp[i]-1;}}return dp[n];
}
当然,可以发现转移至于i-1状态有关,所以可以使用滚动数组优化空间
public int addMinimum(String word) {int n=word.length();int dp_0=0;int dp_1=0;for(int i=0;i<n;i++){dp_1=dp_0+2;if(i<n-1&&word.charAt(i+1)>word.charAt(i)){dp_1=dp_0-1;}dp_0=dp_1;}return dp_1;
}
方法三 直接拼接
参考:官方题解
当前字符小于等于前面字符说明它们一定不在同一组 abc 中,只需要添置若干字符过渡这两者即可。例如 b前面是 c,则需要在中间添置 a,又例如 b 前面是 b,则需要在中间添置 ca。
以上两种情况可以用一个模型来表示,设当前字符是 x,前面字符是 y,那么需要添置的字符个数为 (x−y−1+3)mod 3。其中 +3 再对 3取模,可以应对 x 小于等于 y 的情况。
最后还需要处理头尾两个字符,word[0] 前面添置 word[0]−‘a′ 个字符,word[n−1]后面添置 ‘c′−word[n−1]个字符。两个可以合并为 word[0]−word[n−1]+2
时间复杂度:O(n)
空间复杂度:O(1)
public int addMinimum(String word) {int n=word.length();int res=0;if(n==1)return 2;res+=word.charAt(0)-word.charAt(n-1)+2;for(int i=0;i<n-1;i++){int count=word.charAt(i+1)-word.charAt(i)-1+3;res+=count%3;}return res;}
方法四 计算组数
计算递增序列的组——也就是每一个递增序列都是一个组,然后使用一个变量count记录当前递增序列的长度,需要插入的字符数=3-count。在不满足递增的时候才会计算需要插入的字符数,并且重置count。
时间复杂度:O(n)。n是word的长度
空间复杂度:O(1)
public int addMinimum(String word) {int n=word.length();if(n==1){return 2;}int res=0;int count=1;for(int i=0;i<n-1;i++){if(word.charAt(i+1)<=word.charAt(i)){res+=3-count;count=1;}else{count++;}}return res+(3-count);}
有任何问题,欢迎评论区交流,欢迎评论区提供其它解题思路(代码),也可以点个赞支持一下作者哈😄~
相关文章:

2024.1.11力扣每日一题——构造有效字符串的最少插入数
2024.1.11 题目来源我的题解方法一 暴力模拟方法二 动态规划方法三 直接拼接方法四 计算组数 题目来源 力扣每日一题;题序:2645 我的题解 方法一 暴力模拟 直接模拟,根据题意可知 若是abc则不用插入,若是ab,ac,bc这需要 插入一…...

软件测试|如何使用Selenium处理隐藏元素
简介 我们在使用selenium进行web自动化测试时,有时候会遇到元素被隐藏,从而无法对元素进行操作,导致我们的用例报错的情况。当我们遇到元素被隐藏的情况时,需要先对隐藏的元素进行处理,才能继续进行我们的操作&#x…...
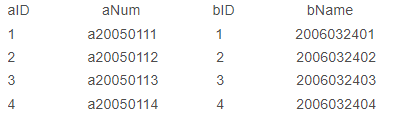
第三次面试总结 - 吉云集团 - 全栈开发
🧸欢迎来到dream_ready的博客,📜相信您对专栏 “本人真实面经” 很感兴趣o (ˉ▽ˉ;) 专栏 —— 本人真实面经,更多真实面试经验,中大厂面试总结等您挖掘 目录 总结(非详细) 面试内…...
buuctf-Misc 题目解答分解118-120
118.[INSHack2017]sanity 打开压缩包就是一个md 文件 typora 打开 发现flag INSA{Youre_sane_Good_for_you} 119.粽子的来历 解压压缩包 ,得到文件夹如下 用010 editor 打开 我是A.doc 这个有些可以 都改成FF 保存 然后再次打开 docx 文件就发现了屈原的诗 其他b…...

Hive数据定义(1)
hive数据定义是hive的基础知识,所包含的知识点有:数据仓库的创建、数据仓库的查询、数据仓库的修改、数据仓库的删除、表的创建、表的删除、内部表、外部表、分区表、桶表、表的修改、视图。本篇文章先介绍:数据仓库的创建、数据仓库的查询、…...
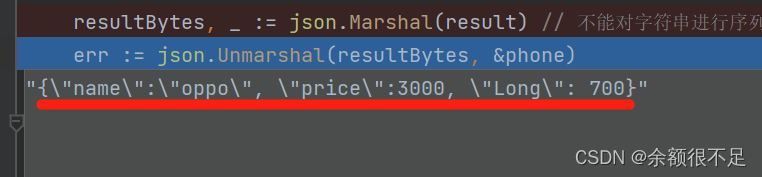
golang 反序列化出现json: cannot unmarshal string into Go value of type model.Phone
项目场景: 今天在项目公关的过程中,需要对interface{}类型进行转换为具体结构体 问题描述 很自然的用到了resultBytes, _ : json.Marshal(result),然后对resultBytes进行反序列化转换为对应的结构体err : json.Unmarshal(resultBytes, &…...
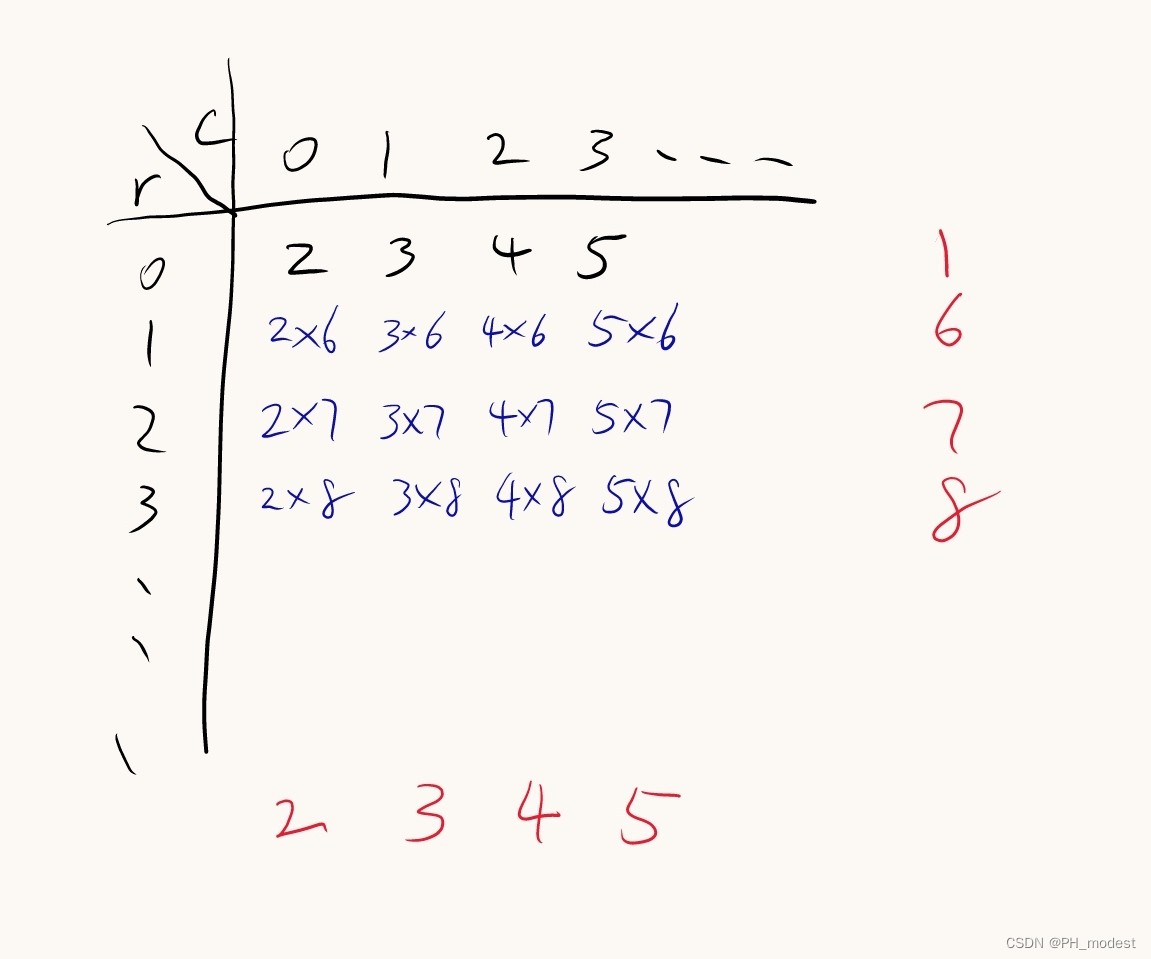
【闯关练习】—— 1400分(构造)
🌏博客主页:PH_modest的博客主页 🚩当前专栏:cf闯关练习 💌其他专栏: 🔴每日一题 🟡 C跬步积累 🟢 C语言跬步积累 🌈座右铭:广积粮,缓…...

Qt QProgressBar进度条控件
文章目录 1 属性和方法1.1 值1.2 方向1.3 外观1.4 信号和槽 2 实例2.1 布局2.2 代码实现 QProgressBar是进度条控件,进度条用来指示任务的完成情况 1 属性和方法 QProgressBar有很多属性,完整的可查看帮助文档。这里以QProgressBar为例,列出…...
【新】Unity Meta Quest MR 开发(一):Passthrough 透视配置
文章目录 📕教程说明📕配置透视的串流调试功能📕第一步:设置 OVRManager📕第二步:添加 OVRPassthroughLayer 脚本📕第三步:在场景中添加虚拟物体📕第四步:设置…...

快速排序【hoare版本】【挖坑法】【双指针法】(数据结构)
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中 的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均…...
class_5:在c++中一个类包含另一个类的对象叫做组合
#include <iostream> using namespace std;class Wheel{ public://成员数据string brand; //品牌int year; //年限//真正的成员函数void printWheelInfo(); //声明成员函数 };void Wheel::printWheelInfo() {cout<<"我的轮胎品牌是:"<…...

Linux - No space left on device
问题描述 No space left on device 原因分析 说明在服务器设备上的存储空间已经满了,不能再上传或者新建文件夹或者文件等。 解决方案 确认查看服务器系统的磁盘使用情况是否是真的已经没有剩余空间,复制下面命令在服务器上运行,然后发现如果…...
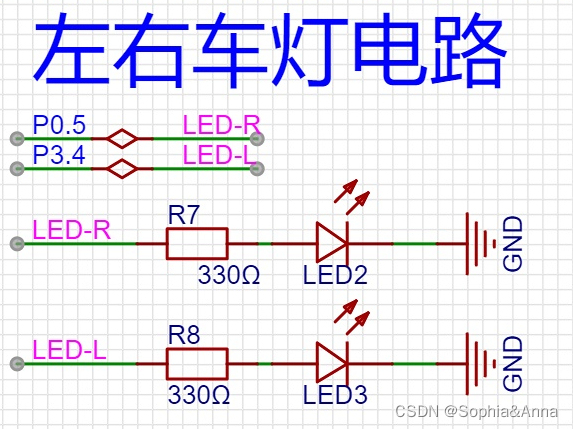
STC8H8K蓝牙智能巡线小车——2. 点亮左右转弯灯与危险报警灯
任务调用示例 RTX 51 TNY 可做多任务调度,API较为简单。 /* 接口API */// 创建任务 extern unsigned char os_create_task (unsigned char task_id); // 结束任务 extern unsigned char os_delete_task (unsigned char task_id);// 等待 extern unsig…...
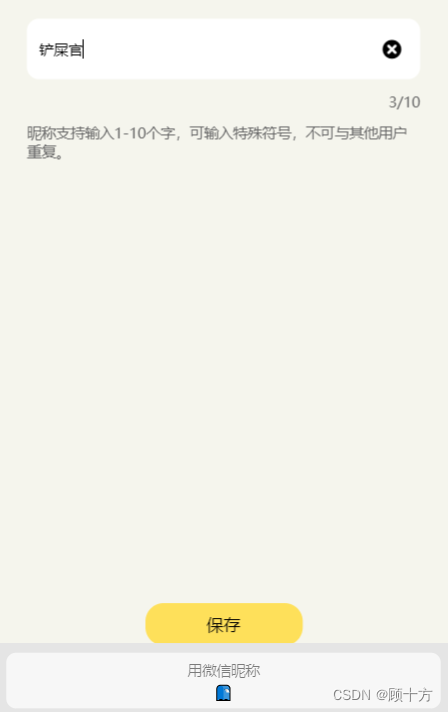
【微信小程序独立开发 3】个人资料页面编写
这一节完成用户个人信息昵称的填写和获取 上节编写完成后的页面如下所示: 首先进行用户昵称编辑功能的编写,铲屎官昵称采用了navigator标签,当点击昵称时会自动跳转到昵称编辑页面。 首先输入昵称编辑界面的导航栏名称 {"usingCompone…...

Linux笔记:Linux中的文件系统权限
在Red Hat Enterprise Linux 或其他类似的Linux发行版中,全局umask设置通常在几个不同的系统级配置文件中定义。以下是一些可能设置umask的地方: (1)/etc/profile: 这是为系统上的所有用户设置全局环境变量和启动程序的地方。通…...
Android基于Matrix绘制PaintDrawable设置BitmapShader,以手指触点为中心显示原图的圆切图,Kotlin(4)
Android基于Matrix绘制PaintDrawable设置BitmapShader,以手指触点为中心显示原图的圆切图,Kotlin(4) 这篇 Android基于Matrix绘制PaintDrawable设置BitmapShader,以手指触点为中心显示原图像圆图,Kotlin&am…...

WARNING: REMOTE HOST IDENTIFICATION HAS CHANGED!
问题背景 当我们尝试通过SSH(Secure Shell)连接到远程服务器时,有时会遇到一个警告信息:“WARNING: REMOTE HOST IDENTIFICATION HAS CHANGED!”。这个消息表明SSH客户端检测到远程主机的身份(即其SSH密钥)…...

深入理解JVM虚拟机第三十九篇:JVM中新生代和老年代相关参数设置
😉😉 欢迎加入我们的学习交流群呀! ✅✅1:这是孙哥suns给大家的福利! ✨✨2:我们免费分享Netty、Dubbo、k8s、Mybatis、Spring、Security、Docker、Grpc、消息中间件、Rpc、SpringCloud等等很多应用和源码级别高质量视频和笔记资料,你想学的我们这里都有! 🥭🥭3:…...

打造创新的金融数据平台,加速数字化和智能化转型丨PingCAP 官网金融行业专区上线
自诞生以来,TiDB 的原生分布式架构在强一致性、高可用性和可扩展性等方面与金融级业务需求高度契合,早期版本即为包括北京银行在内的金融用户提供服务。 TiDB 的核心能力始终源自与中国金融用户的共同创造。作为金融级分布式数据库,TiDB 在国…...
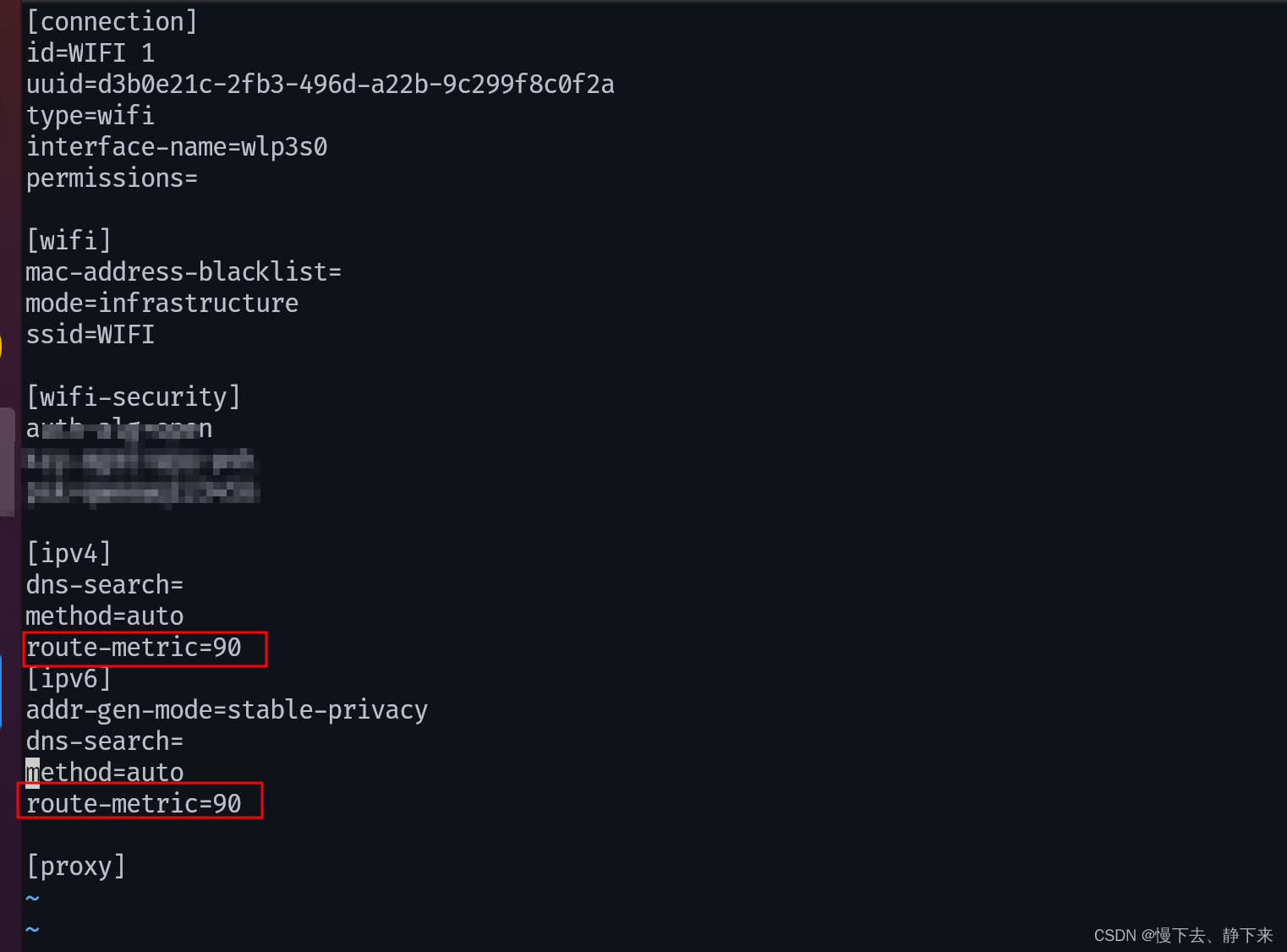
记ubuntu2004通过NetworkManager修改网络的优先级
这里写自定义目录标题 前言步骤 前言 起因在于万恶的校园网,突然台式有线死活没法认证(感觉是IP冲突了?另外一台电脑同样的系统就没有问题,连路由器WIFI也是可以的,路由器设置的是桥接模式,有没有大佬提供…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

算法刷题-回溯
今天给大家分享的还是一道关于dfs回溯的问题,对于这类问题大家还是要多刷和总结,总体难度还是偏大。 对于回溯问题有几个关键点: 1.首先对于这类回溯可以节点可以随机选择的问题,要做mian函数中循环调用dfs(i&#x…...
