数据结构二叉树--堆(数据结构实现和堆排序的一种实现)
堆是一个数据结构
逻辑结构:完全二叉树(要求父节点大于孩子节点或者小于孩子节点)
存储结构:顺序存储
typedef int DataType;
typedef struct Heap{DataType*data;int size;int capacity;
}Heap;void InitHeap(Heap*pH)
{assert(pH);pH->data=NULL;pH->size=0;pH->capacity=0;
}void expand(Heap*pH)
{DataType*p=realloc(pH->a,sizeof(DataType)*(pH->capacity+2));if(p==NULL){printf("%s",strerror(errno)); }pH->data=p;pH->capacity+=2;
}void Swap(int*n1,int*n2)
{int tmp=*n1;*n1=*n2;*n2=tmp;
}void AdjustUp(Heap*pH,int child)
{while(child>0){int parent=(child-1)/2;if(data[child]<data[parent]){Swap(&data[child],&data[parent]);child=parent;}else{break;}}
}void HeapPush(Heap*pH,int n)
{assert(pH);expand(pH);pH->data[pH->size++]=n;AdjustUp(pH->data,pH->size-1);
}void AdjustDown(DataType*data,int parent,int size)
{int child=2*parent+1;while(child>n&&child+1>n){if(data[child]>data[child+1]){child+=1;}if(data[parent]>data[child]){Swap(&data[parent],&data[child]);parent=child;child=2*parent+1;}}}void HeapPop(Heap*pH)
{assert(pH->size);Swap(&pH->data[0],&pH->data[pH->size-1]);pH->size--;AdjustDown(pH->data,0,pH->size);
}这是堆的基本操作,我们如果有一个数组,想借助堆这个数据结构利用额外的空间来实现排序,那么先依次将数据放入堆中,再依次删除并将删除的数据放入到数组中完成排序。每一次插入的时间复杂度最多都是O(logN),删除也一样,比起之前冒泡排序O(n^2)要好一些。
但是有很大的缺点,首先就是要有一个堆,每次都先这样实现堆很麻烦,还有一点是空间复杂度为O(N),有额外开辟的空间。我们可以这样做:用一个指针从左到右依次扫描数组,向上调整算法的使用前提是本身为堆,那我们从下标为1的元素开始,扫描到一个相当于插入了一个,然后用向上调整算法调整为堆,再扫描下一个+调整,扫描完最后一个元素为止。那么这个数组就是一个堆了,如果我们想升序排列,则整理为大堆,先找最大的数据放在最后,如果想降序排列就先找最小的,也就是小堆。why?如果我们排列升序,先找最小的,那么后面的元素怎么办?需要重新整理成堆,时间复杂度为N^2*logN,这比N^2的时间复杂度还要高,没必要搞这么一堆出来了,所以排升序找最大的。排成堆+交换就找出了最大的,然后排成堆+交换就找出了次大的,以此类推即可。这个做法的本质就是在一个数组上模拟堆的插入和删除,扫描增加一个就是插入,交换一次就是删除。
相关文章:
)
数据结构二叉树--堆(数据结构实现和堆排序的一种实现)
堆是一个数据结构 逻辑结构:完全二叉树(要求父节点大于孩子节点或者小于孩子节点) 存储结构:顺序存储 typedef int DataType; typedef struct Heap{DataType*data;int size;int capacity; }Heap;void InitHeap(Heap*pH) {asser…...

【Linux】 nohup命令使用
nohup命令 nohup是Linux和Unix系统中的一个命令,其作用是在终端退出时,让进程在后台继续运行。它的全称为“no hang up”,意为“不挂起”。nohup命令可以让你在退出终端或关闭SSH连接后继续运行命令。 nohup 命令,在默认情况下&…...

多维时序 | Matlab实现GRO-CNN-LSTM-Attention淘金算法优化卷积神经网络-长短期记忆网络结合注意力机制多变量时间序列预测
多维时序 | Matlab实现GRO-CNN-LSTM-Attention淘金算法优化卷积神经网络-长短期记忆网络结合注意力机制多变量时间序列预测 目录 多维时序 | Matlab实现GRO-CNN-LSTM-Attention淘金算法优化卷积神经网络-长短期记忆网络结合注意力机制多变量时间序列预测效果一览基本介绍程序设…...
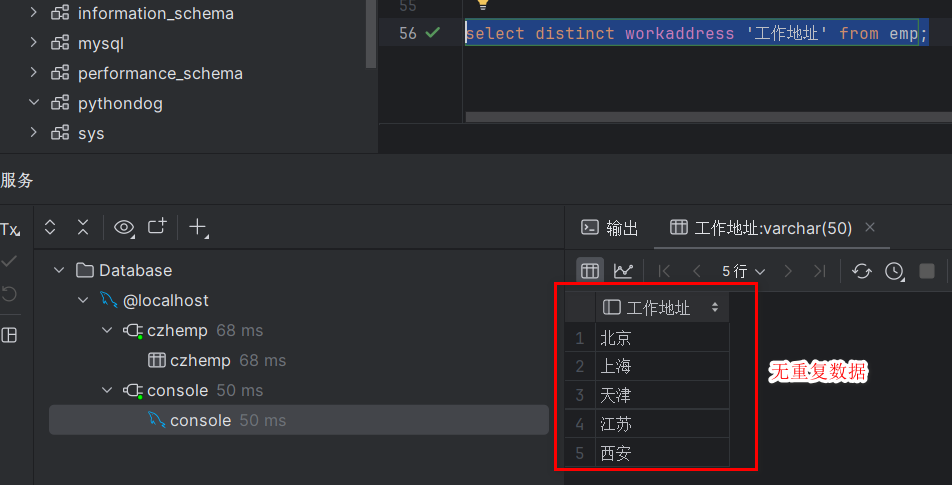
SQL-DQL-基础查询
🎉欢迎您来到我的MySQL基础复习专栏 ☆* o(≧▽≦)o *☆哈喽~我是小小恶斯法克🍹 ✨博客主页:小小恶斯法克的博客 🎈该系列文章专栏:重拾MySQL 🍹文章作者技术和水平很有限,如果文中出现错误&am…...
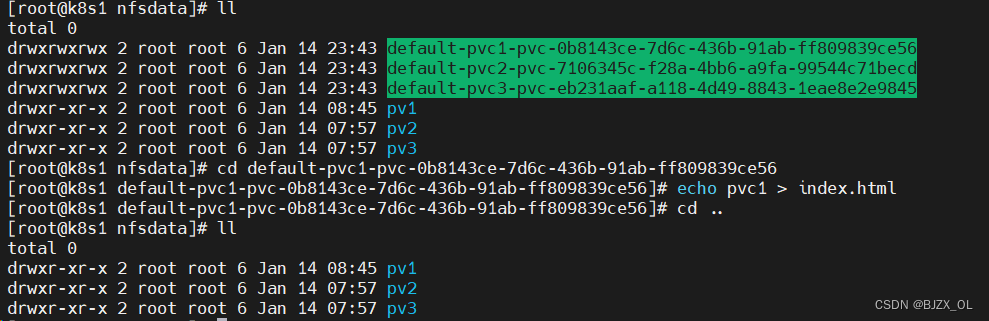
Kubernetes (十三) 存储——持久卷-动静态分配
一. 简介 二. NFS持久化存储步骤(静态分配) 1. 集群外…...
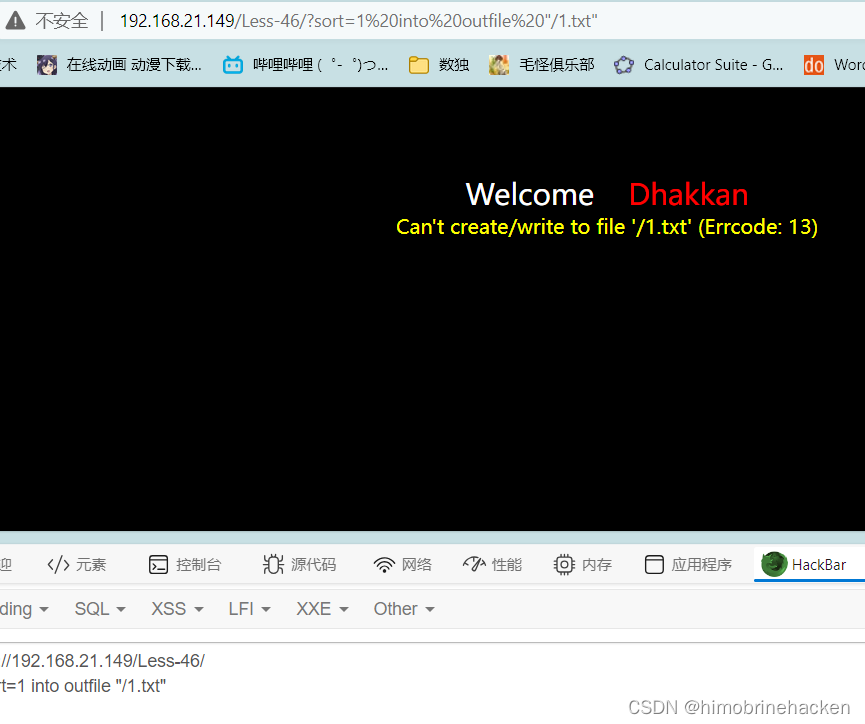
order by之后的injection(sqllabs第四十六关)
order by相关注入知识 这一关的sql语句是利用的order by 根据输入的id不同数据排序不一样可以确定就是order by order by后面无法使用ubion注入(靠找不到) 可以利用后面的参数进行攻击 1)数字 没作用考虑布尔类型 rand和select ***都可以 …...

C++ 树与图的广度优先遍历 || 模版题 :图中点的层次
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环。 所有边的长度都是 1 ,点的编号为 1∼n 。 请你求出 1 号点到 n 号点的最短距离,如果从 1 号点无法走到 n 号点,输出 −1 。 输入格式 第一行包含两个整数 n 和 m 。 …...
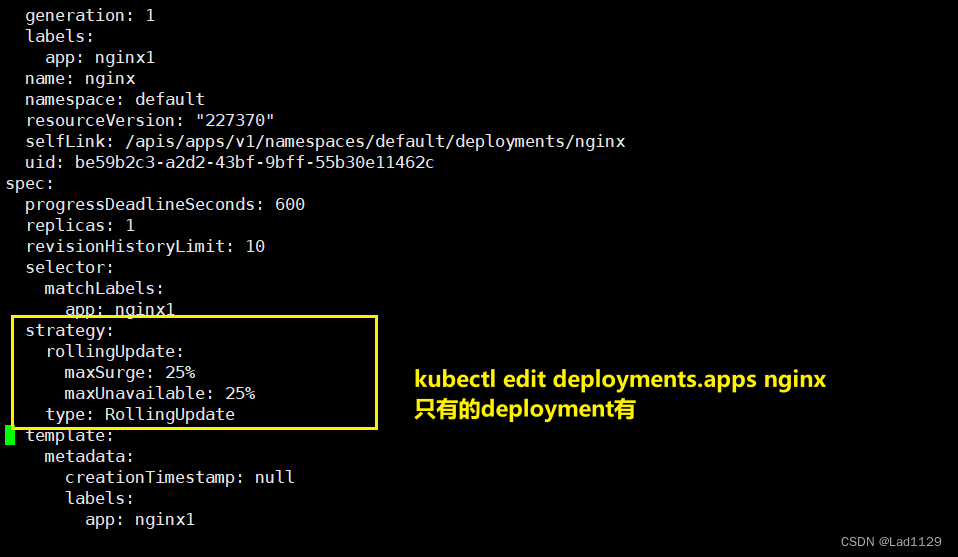
k8s---pod控制器
pod控制器发的概念: 工作负载,workload用于管理pod的中间层,确保pod资源符合预期的状态。 预期状态: 1、副本数 2、容器重启策略 3、镜像拉取策略 pod出故障的出去等等 pod控制器的类型: 1、replicaset…...

2024.1.11力扣每日一题——构造有效字符串的最少插入数
2024.1.11 题目来源我的题解方法一 暴力模拟方法二 动态规划方法三 直接拼接方法四 计算组数 题目来源 力扣每日一题;题序:2645 我的题解 方法一 暴力模拟 直接模拟,根据题意可知 若是abc则不用插入,若是ab,ac,bc这需要 插入一…...

软件测试|如何使用Selenium处理隐藏元素
简介 我们在使用selenium进行web自动化测试时,有时候会遇到元素被隐藏,从而无法对元素进行操作,导致我们的用例报错的情况。当我们遇到元素被隐藏的情况时,需要先对隐藏的元素进行处理,才能继续进行我们的操作&#x…...
第三次面试总结 - 吉云集团 - 全栈开发
🧸欢迎来到dream_ready的博客,📜相信您对专栏 “本人真实面经” 很感兴趣o (ˉ▽ˉ;) 专栏 —— 本人真实面经,更多真实面试经验,中大厂面试总结等您挖掘 目录 总结(非详细) 面试内…...
buuctf-Misc 题目解答分解118-120
118.[INSHack2017]sanity 打开压缩包就是一个md 文件 typora 打开 发现flag INSA{Youre_sane_Good_for_you} 119.粽子的来历 解压压缩包 ,得到文件夹如下 用010 editor 打开 我是A.doc 这个有些可以 都改成FF 保存 然后再次打开 docx 文件就发现了屈原的诗 其他b…...

Hive数据定义(1)
hive数据定义是hive的基础知识,所包含的知识点有:数据仓库的创建、数据仓库的查询、数据仓库的修改、数据仓库的删除、表的创建、表的删除、内部表、外部表、分区表、桶表、表的修改、视图。本篇文章先介绍:数据仓库的创建、数据仓库的查询、…...
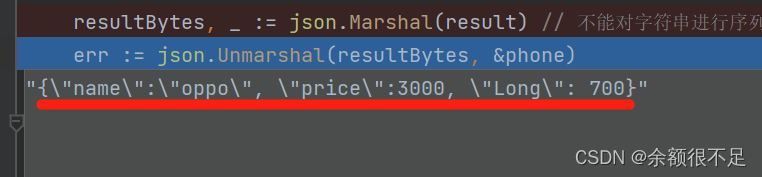
golang 反序列化出现json: cannot unmarshal string into Go value of type model.Phone
项目场景: 今天在项目公关的过程中,需要对interface{}类型进行转换为具体结构体 问题描述 很自然的用到了resultBytes, _ : json.Marshal(result),然后对resultBytes进行反序列化转换为对应的结构体err : json.Unmarshal(resultBytes, &…...
【闯关练习】—— 1400分(构造)
🌏博客主页:PH_modest的博客主页 🚩当前专栏:cf闯关练习 💌其他专栏: 🔴每日一题 🟡 C跬步积累 🟢 C语言跬步积累 🌈座右铭:广积粮,缓…...

Qt QProgressBar进度条控件
文章目录 1 属性和方法1.1 值1.2 方向1.3 外观1.4 信号和槽 2 实例2.1 布局2.2 代码实现 QProgressBar是进度条控件,进度条用来指示任务的完成情况 1 属性和方法 QProgressBar有很多属性,完整的可查看帮助文档。这里以QProgressBar为例,列出…...
【新】Unity Meta Quest MR 开发(一):Passthrough 透视配置
文章目录 📕教程说明📕配置透视的串流调试功能📕第一步:设置 OVRManager📕第二步:添加 OVRPassthroughLayer 脚本📕第三步:在场景中添加虚拟物体📕第四步:设置…...

快速排序【hoare版本】【挖坑法】【双指针法】(数据结构)
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中 的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均…...
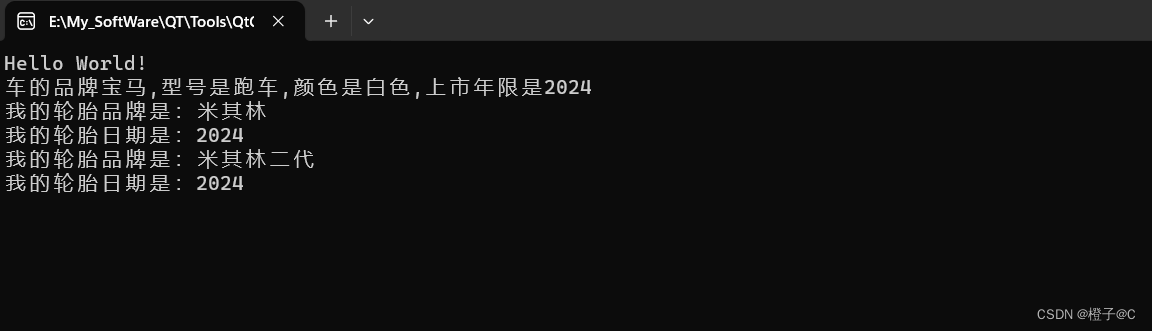
class_5:在c++中一个类包含另一个类的对象叫做组合
#include <iostream> using namespace std;class Wheel{ public://成员数据string brand; //品牌int year; //年限//真正的成员函数void printWheelInfo(); //声明成员函数 };void Wheel::printWheelInfo() {cout<<"我的轮胎品牌是:"<…...

Linux - No space left on device
问题描述 No space left on device 原因分析 说明在服务器设备上的存储空间已经满了,不能再上传或者新建文件夹或者文件等。 解决方案 确认查看服务器系统的磁盘使用情况是否是真的已经没有剩余空间,复制下面命令在服务器上运行,然后发现如果…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
