2024.1.14~1.20 周内刷题总结
2024.1.14~1.20 周内刷题总结
- [ABC158F] Removing Robots 题解
- [ABC145F] Laminate 题解
- [ABC254G] Elevators 题解(坑点总结)
- [ARC160C] Power Up 题解
- [ABC203F] Weed 题解
- Shopping
- 时代的眼泪
[ABC158F] Removing Robots 题解
\qquad 题面
\qquad 本题的连锁反应显然在指引我们建图。但是建出 D A G DAG DAG 后,我们发现转移也是很难搞的。在这里,我们引入一个小技巧:关于这类 D A G DAG DAG 表示连锁关系的 d p dp dp 中, D A G DAG DAG 可以退化成一棵树,随后进行树形 d p dp dp。原先的连锁关系变为树上的祖先关系,而树形 d p dp dp 就会十分好写。
\qquad Code
[ABC145F] Laminate 题解
\qquad 题面
\qquad 首先,我们要明确一点:这 K K K 根被改变的柱子一定不会给总代价带来贡献。所以我们可以视为删去了 K K K 根柱子,留下了 n − K n-K n−K 根柱子。至此,我们便可设计状态: d p i , j dp_{i,j} dpi,j 表示考虑完了前 i i i 根柱子,保留了 j j j 根柱子的最小代价。转移很简单。
\qquad Code
[ABC254G] Elevators 题解(坑点总结)
\qquad 题面
\qquad 本题的主要目标就是让我们从第 x i x_i xi 栋楼的第 y i y_i yi 层跳到第 z i z_i zi 栋楼的第 w i w_i wi 层。在这里,我们假设 y i < w i y_i<w_i yi<wi。若大于,交换即可。
\qquad 首先要确定一点:我们一定只会向上坐电梯,向下坐一定是不优的,因为向下之后早晚要再上去。所以,我们的问题就可以简化为:最少需要换几栋楼才能让我们从 y i y_i yi 层到达 w i w_i wi 层。
\qquad 接着,我们再贪心地想:如果我们现在要坐电梯向上走,那么我们坐到当前楼中能坐到的最高层一定是不亏的。毕竟迟早都要上到这么高,早上去一会肯定没问题。这就启发我们要把一层楼中有重叠部分的电梯合并成一个大电梯来处理。
\qquad 现在,我们思考:如何判断我们能否坐到第 w i w_i wi 层呢?我们想:假设现在我们从第 p p p 层出发,能坐到的最高的层数为 q q q。如果 q ≥ w i q\geq w_i q≥wi,那么是不是就能说明我们一定能坐到第 w i w_i wi 层呢?这启发我们可以记录从第 i i i 层出发,能坐到的最高的层数,记为 f i f_i fi。若 f y i ≥ w i f_{y_i}\geq w_i fyi≥wi,那就说明一定能坐到第 w i w_i wi 层。
\qquad 但是,题目要求我们求出最小的转楼次数。我们如何将转楼次数与最高层数联系起来呢?我们可以大力添加状态的维度。设 f i , j f_{i,j} fi,j 表示从 i i i 出发,转 j j j 次楼能坐到的最高层数。这显然是可搞的。但是时空复杂度是接受不了的。分析这一状态,我们发现,随着转楼次数的升高,能坐到的最高层数一定是不降的,所以我们可以考虑倍增的写法,设 f i , j f_{i,j} fi,j 表示从 i i i 出发,转 2 j 2^j 2j 次楼能坐到的最高层数,用线段树可以先求出 f i , 0 f_{i,0} fi,0,然后用倍增求出剩下的 f i , j f_{i,j} fi,j 即可。
\qquad 坑点:1、区间合并的时候,右端点是不断在更新的!当前已合并区间的右端点是前面所有右端点的 m a x max max!2、倍增查询时,要先将初始的 y , w y,w y,w 跳到所在电梯的最高层、最低层。因为倍增记录的是跨楼次数,但是这一初始化的进行是不需要跨楼的。
\qquad Code
[ARC160C] Power Up 题解
\qquad 题面
\qquad 本题如果直接硬对着序列设计状态(例如设计 f i f_i fi 表示考虑到第 i i i 个数可构成的集合的方案数)是不好转的,因为相等的数可能有很多,合并之后的情况很复杂。再者,我们观察到本题的值域较小,而且合并的过程也主要和值与其个数有关,所以我们大力设状态: d p i , j dp_{i,j} dpi,j 表示在合并数字 i i i 之前还剩 j j j 个 i i i 的方案数。那么转移也是好转的: d p i , a i + j = ∑ k = j × 2 N U M m a x i − 1 d p i − 1 , k dp_{i,a_i+j}=\sum_{k=j\times 2}^{NUMmax_{i-1}}dp_{i-1,k} dpi,ai+j=∑k=j×2NUMmaxi−1dpi−1,k。 N U M m a x i − 1 NUMmax_{i-1} NUMmaxi−1 表示 i − 1 i-1 i−1 最多有多少个。乍一看,这是一个二维的转移式。但是,通过计算可得,它的总状态数是相当的少的,大概只有 2 N 2N 2N 范围,所以我们直接大力转移即可。转移时需要用到后缀和、滚动数组优化,不过都很简单。
\qquad Code
[ABC203F] Weed 题解
\qquad 题面
\qquad 首先,本题的贪心策略显然是错误的,想 H a c k Hack Hack 也很简单。所以我们考虑设计 d p dp dp 状态。本题要求两个值:1、最小的操作次数;2、满足操作次数最小的基础上,预先拔掉草的数量最小。我们可以设 d p i , j dp_{i,j} dpi,j 表示操作了 j j j 次,解决了前 i i i 株草,所需要预先拔掉的最少的草的数量。设计这个状态主要的一点好处就是同时包含了题目要求的两个值,通过判断 d p i , j ≤ K dp_{i,j}\leq K dpi,j≤K 来判断 j j j 次操作是否可行。转移很显然,每株草有被预先处理和不被预先处理两种选择。式子很好写。由于每次操作相当于折半操作,所以最多进行 l o g log log 次操作,状态数为 n l o g nlog nlog 级别的,直接跑可过。
\qquad Code
Shopping
\qquad 题面
\qquad 本题对树背包的限制是:选取的物品在树上一定要连成一个连通块。这一点可以启发我们用点分治来解决。不过正常去跑树上多重背包显然是会 T T T 的。在这里引入一个树形 d p dp dp 的优化方法:求出树的 d f s dfs dfs 序后在 d f s dfs dfs 序上 d p dp dp。再加上一个单调队列优化多重背包,便可做到 O ( T n m log d ) O(Tnm\log d) O(Tnmlogd) 的时间复杂度。
\qquad Code
时代的眼泪


\qquad 网络流妙题。
\qquad 前面几档状压的分就不说了,考虑 K = 1 K=1 K=1 怎么搞。通过前面的状压我们得到了两条性质:1、可以将 A A A 类事件删减成一个 x x x 递增, y y y 递减的形状;2、 B B B 类事件覆盖一整个区间一定是优的。在这两条性质的基础上,我们便可以列一个 d p dp dp 式子: f i f_i fi 表示前 i i i 个 A A A 类事件被覆盖的最小代价。转移很好写: f i = min ( f j − 1 + max ( x i − x k , 0 ) + max ( y j , y k , 0 ) ) f_i=\min(f_{j-1}+\max(x_i-x_k, 0)+\max(y_j,y_k,0)) fi=min(fj−1+max(xi−xk,0)+max(yj,yk,0)), k k k 是我们枚举的使用哪个 B B B 类点。这个 d p dp dp 是很难优化的,我们考虑用更巧妙的方法来完成它。我们把所有事件的 x , y x,y x,y 坐标都存起来,并分别从小到大排序。然后我们考虑建图: x i x_i xi 向 x i + 1 x_{i+1} xi+1 建一条边权为 x i + 1 − x i x_{i+1}-x_i xi+1−xi 的边,同时连一条边权为 0 0 0 的反向边。 y i + 1 y_{i+1} yi+1 向 y i y_i yi 连一条边权为 y i + 1 − y i y_{i+1}-y_i yi+1−yi 的边,同时连一条边权为 0 0 0 的反向边。对于每个B类事件,我们从其 y y y 向 x x x 连一条边权为 0 0 0 的边。这样,上面转移式中的 max + max \max + \max max+max 就可以表示为从 y j y_j yj 到 x i x_i xi 的最短路。原因如下图:
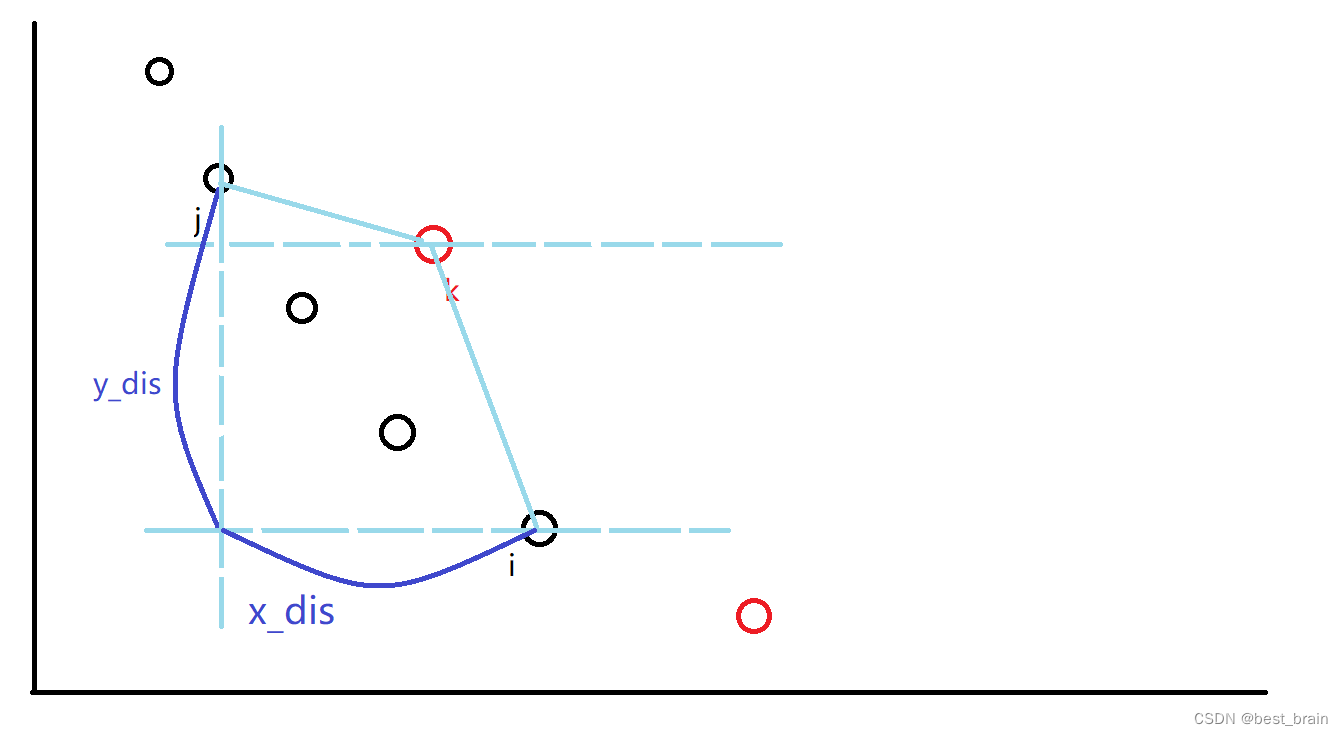
\qquad 我们想从 j j j 转移到 i i i, y y y 是从大指向小的, x x x 是从小指向大的,所以上述建图方法跑出来的最短路就是 B B B 类事件需要移动的最短距离。但是这样转移还是 O ( n 2 ) O(n^2) O(n2) 的,怎么优化呢?上面的性质 2 2 2 已经解决了这一问题。性质 2 2 2 旨在表明一个 A A A 类事件最多被覆盖一次,所以我们跑完 y j y_j yj 到 x i x_i xi 的最短路后,下一次一定是从 y i + 1 y_{i+1} yi+1 开始往后跑。所以我们对于每个A类事件,从 x i x_i xi 向 y i + 1 y_{i+1} yi+1 连一条边权为 0 0 0 的边,最后跑一个 y 1 y_1 y1 到 x n x_n xn 的最短路就是答案。
\qquad 那么对于 K K K 为任意值怎么搞呢?那就相当于在图上找 K K K 条路径并让他们总权值最小。这里边 B B B 类事件连出来的边只能被经过一次,因为一个 B B B 类事件最多被移动到一个位置。这个模型就非常像费用流。我们把上图中的边权变为费用流中的费用,让 B B B 类事件连的边的容量为 1 1 1,其余边容量为 I N F INF INF,跑一个流量为 K K K 的最小费用最大流即可。但是本题直接按照正常的基于 s p f a spfa spfa 寻找增广路的费用流去跑是会 T T T 的。而 D i j k s t r a Dijkstra Dijkstra 跑不了带负边权的流网络。怎么办呢?我们可以采用 J o h n s o n Johnson Johnson 算法的思想,给每个点赋一个势能,在增广的过程中动态更新势能即可。这样就可以用 D i j Dij Dij 来增广。总时间复杂度为 O ( K n log n ) O(Kn\log n) O(Knlogn),常数较大。
\qquad Code
相关文章:

2024.1.14~1.20 周内刷题总结
2024.1.14~1.20 周内刷题总结 [ABC158F] Removing Robots 题解[ABC145F] Laminate 题解[ABC254G] Elevators 题解(坑点总结)[ARC160C] Power Up 题解[ABC203F] Weed 题解Shopping时代的眼泪 [ABC158F] Removing Robots 题解 \qquad 题面 \qquad 本题的连…...

徐州数字孪生元宇宙赋能工业智能制造,助力传统制造业数字化转型
徐州数字孪生元宇宙赋能工业智能制造,助力传统制造业数字化转型。在徐州市制造业企业数字化转型的过程中,数字孪生技术的应用已经取得了显著成效。一方面,企业的生产效率得到了显著提高,产品质量也得到了有效保障。另一方面&#…...

智云谷再获资本市场青睐,完成数千万元A+轮融资
近日,深圳前海智云谷科技有限公司(以下简称“智云谷”)完成数千万元A轮融资,本轮融资由青松基金独家投资,多维资本担任独家融资财务顾问。本轮融资资金将用于扩大新技术研发投入、智能工厂扩产、加速产品交付ÿ…...
| 文章顶部信息(Top matter))Part 1)
ACM论文LaTeX模板解析(三)| 文章顶部信息(Top matter))Part 1
本文收录于专栏:ACM 论文 LaTeX模板解析,本专栏将会围绕ACM 论文 LaTeX模板解析持续更新。欢迎点赞收藏关注! 文章目录 有许多命令可以设置文章的顶部信息或(计算机科学术语)元数据。它们建立了出版物名称、文章标题、…...

[GDOUCTF 2023]受不了一点
[GDOUCTF 2023]受不了一点 wp 题目代码: <?php error_reporting(0); header("Content-type:text/html;charsetutf-8"); if(isset($_POST[gdou])&&isset($_POST[ctf])){$b$_POST[ctf];$a$_POST[gdou];if($_POST[gdou]!$_POST[ctf] &&…...

精心挑选免费好用的api,推荐给大家
企业基本信息:通过公司名称/公司ID/注册号或社会统一信用代码获取企业基本信息,企业基本信息包括公司名称或ID、类型、成立日期、经营状态、注册资本、法人、工商注册号、统一社会信用代码、组织机构代码、纳税人识别号等字段信息。 AI绘画-Stable Diff…...

(001)window 使用 OpenObserve
文章目录 安装上传数据报错附录 安装 1.下载安装包: 2. window 设置环境变量: ZO_ETCD_COMMAND_TIMEOUT 600 ZO_ETCD_CONNECT_TIMEOUT 600 ZO_ETCD_LOCK_WAIT_TIMEOUT 600 ZO_INGEST_ALLOWED_UPTO 10000 ZO_ROOT_USER_EMAIL 422615924qq.com ZO_…...

linux发送http请求命令
一、http get请求 1、curl命令不带参 curl “http://www.baidu.com” 如果这里的URL指向的是一个文件或者一幅图都可以直接下载到本地 curl -i “http://www.baidu.com” 显示全部信息 curl -l “http://www.baidu.com” 只显示头部信息 curl -v “http://www.baidu.com”…...
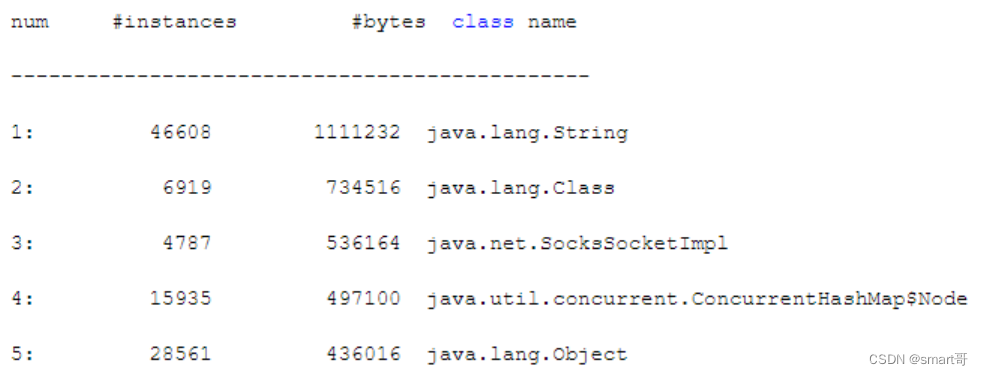
JVM实战(19)——JVM调优工具概述
作者简介:大家好,我是smart哥,前中兴通讯、美团架构师,现某互联网公司CTO 联系qq:184480602,加我进群,大家一起学习,一起进步,一起对抗互联网寒冬 学习必须往深处挖&…...

Windows10无法访问github
亲测有效 1、修改hosts文件 如果电脑是Windows系统:打开 C:\Windows\System32\drivers\etc 找到hosts文件,将对应的Host地址修改为: #github 140.82.112.4 github.com 199.232.69.194 github.global.ssl.fastly.net 如果在保存hosts时遇到…...
)
GIT 分支管理办法(二)
GIT 分支管理办法(二) 一. 大型项目分支管理中存在的痛点 大型项目中需求的上线存在很大的不确定性,而且往往存在多版本、多团队、多开发并行的情况。尤其是大型企业对上线分支中编号的管理十分严苛,严禁夹带上线。这时对于开发…...

Vue面试之Mixins
Vue面试之Mixins 定义Mixins使用Mixins全局MixinsMixins合并策略注意事项命名冲突:过度使用 最近在整理一些前端面试中经常被问到的问题,分为vue相关、react相关、js相关、react相关等等专题,可持续关注后续内容,会不断进行整理~ …...

YOLOv8改进 | 主干篇 | EfficientViT高效的特征提取网络完爆MobileNet系列(轻量化网络结构)
一、本文介绍 本文给大家带来的改进机制是主干网络,一个名字EfficientViT的特征提取网络(和之前发布的只是同名但不是同一个),其基本原理是提升视觉变换器在高效处理高分辨率视觉任务的能力。它采用了创新的建筑模块设计,包括三明治布局和级联…...
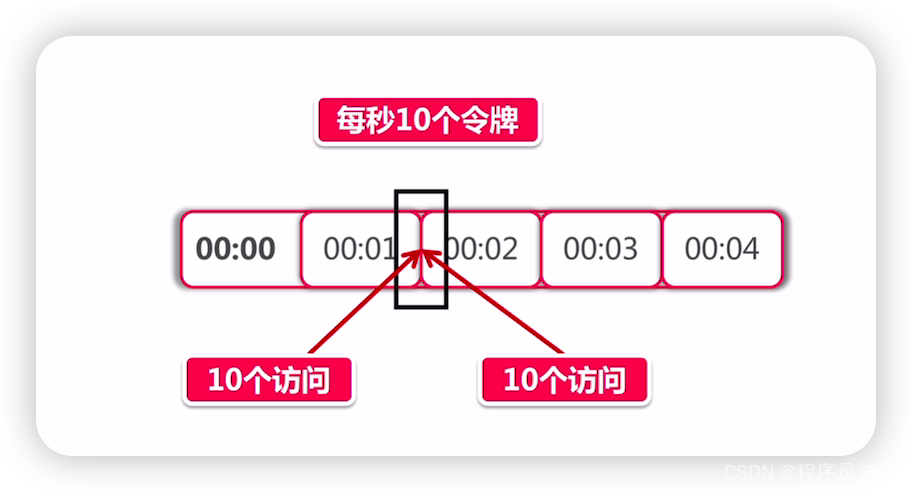
分布式限流要注意的问题
本文已收录至我的个人网站:程序员波特,主要记录Java相关技术系列教程,共享电子书、Java学习路线、视频教程、简历模板和面试题等学习资源,让想要学习的你,不再迷茫。 为什么需要匀速限流 同学们回想一下在Guava小节里…...

git将一个远程分支的部分修改提交到另一个远程分支
将一个远程分支的部分修改提交到另一个远程分支 将一个远程分支的部分修改提交到另一个远程分支,可以使用 git cherry-pick 命令。这个命令可以选择特定的提交(commit)从一个分支应用到另一个分支。 切换到目标本地分支: 首先&am…...

promise是什么怎么使用
Promise 是一种 JavaScript 中的对象,用于处理异步操作。它表示一个最终可能完成(解析)或失败(拒绝)的操作,以及其结果值。 Promise 有三种状态: Pending(待定)&#x…...
国际版WPS Office 18.6.1
【应用名称】:WPS Office 【适用平台】:#Android 【软件标签】:#WPS 【应用版本】:18.6.1 【应用大小】:160MB 【软件说明】:软件日常更新。WPS Office是使用人数最多的移动办公软件。独有手机阅读模式…...

记录一次数据中包含转义字符\引发的bug
后端返回给前端的数据是: { "bizObj": { "current": 1, "orders": [ ], "pages": 2, "records": [ { "from": "1d85b8a4bd33aaf99adc2e71ef02960e", …...
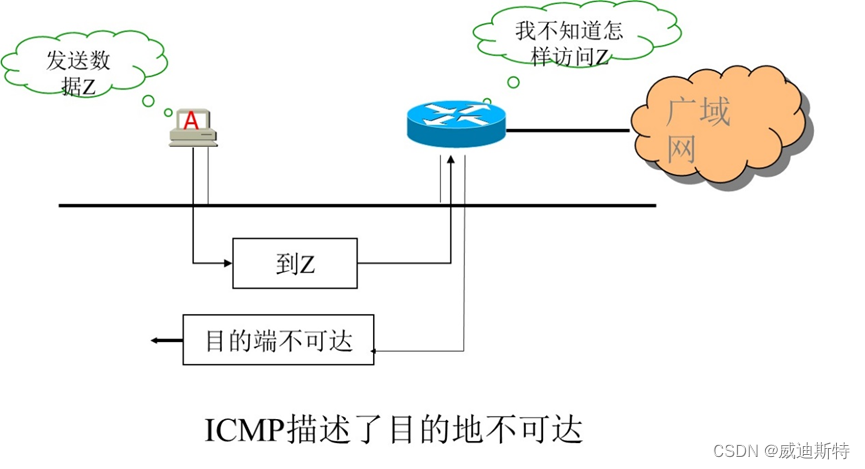
网络协议:ICMP协议及实用工具介绍
目 录 一、ICMP介绍 1、概述 2、功能 3、特点 二、ICMP的数据报文 三、ICMP相关工具 四、主要ICMP工具应用 1、Ping 2、Traceroute (1) 方法1: (2)方法2: 3、Nmap 一、ICMP介绍 1、概述 …...
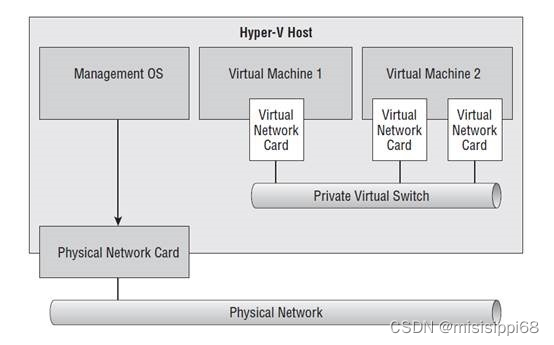
Hyper-V如何设置网络-虚拟交换机设置
Hyper-V如何设置网络-虚拟交换机设置 缘起虚拟交换机类型1. 外部交换机;2. 内部交换机;3. 专用交换机;4.default switch; 虚拟机上openwrt多种网络连接方式 缘起 发现win10还有个虚拟机Hyper-V的功能,不太占资源&…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...
