Codeforces Round 919 (Div. 2)
Problem - A - Codeforces
n个约束条件
a x
求出满足n个约束条件的整数的个数
大于等于x,取最大的
小于等于x,取最小的
然后不等于x的,记录在区间范围内的个数,减去这些
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
int n;
void solve() {cin>>n;vector<int>ans;int l=0,r=2e9;for(int i=0;i<n;i++){int a,x;cin>>a>>x;if(a==1) l=max(l,x);else if(a==2) r=min(r,x);else ans.push_back(x);}int sum=r-l+1;if(sum<0){cout<<0<<endl;return;}int cnt=0;for(auto v:ans){if(v>=l&&v<=r) cnt++;}cout<<sum-cnt<<endl;
}
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--) {solve();}return 0;
}Problem - B - Codeforces
长度为n的数组a
操作:Alice删除最多k个元素,然后Bob最多将x个元素乘以-1
Alice想要全部数之和最大,Bob想要全部数之和最小
Bob肯定是尽可能的从大到小尽可能多的乘以-1,暴力枚举Alice删除的个数(从大的开始删)
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=2e5+10;
int a[N];
int pre[N];
int n,k,x;
void solve() {cin>>n>>k>>x;int sum=0;memset(pre,0,sizeof pre);for(int i=1;i<=n;i++) cin>>a[i],sum+=a[i];sort(a+1,a+1+n);for(int i=1;i<=n;i++) pre[i]=pre[i-1]+a[i];int ans=-2e9;for(int i=0;i<=k;i++){//枚举删除i个int r=n-i;//[r+1,n]删除int l=max((int)1,r-x+1);//[l,r]全变成-1ans=max(ans,sum-2*(pre[r]-pre[l-1])-(pre[n]-pre[r]));}cout<<ans<<endl;
}
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--) {solve();}return 0;
}Problem - C - Codeforces

对于x,y,x=y(mod m)等价于(x-y)mod m=0,即如果m是|x-y|的因子,那么x,y在模m的意义下同余
所以对于某个k值(k是n的因子,一个一个枚举即可),如果存在m大于等于2,满足a1,a1+k,a1+2 * k...在模m的意义下同余,a2,a2+k,a2+2 * k...在模m的意义下同余...那么k就是一个合法解,答案就加1,也就是说每隔k个的在模m的意义下同余,所以直接从头遍历,看其和其后第k个即可,然后都是模m等于0,所以m需要是它们所有的公因数,故求一个最大公因数,如果大于等于2的话就可以
还一种情况,就是每隔k个数都相等,那么最大公因数就是0,也是可行的
trick:
1.对于x,y,x=y(mod m)等价于(x-y)mod m=0,即如果m是|x-y|的因子,那么x,y在模m的意义下同余
2.a1,a1+k,a1+2 * k...在模m的意义下同余,a2,a2+k,a2+2 * k...在模m的意义下同余...也就是说每隔k个的在模m的意义下同余,所以直接从头遍历,看其和其后第k个是否同余即可,由于都是模m为0,所以m是每差k个的两数之差的绝对值的公因数
3.gcd(a,b),令a等于0,那么结果就是b,所以求很多数的最大公因数时,可以初始化为0,这样比较好
4.当所有数都等于x时,如果初始化为0的话,对它们求gcd为0,如果初始化为其中一个数时,那么对它们求gcd则为
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=2e5+10;
int a[N];
int n;
int gcd(int a,int b){if(b==0) return a;return gcd(b,a%b);
}
void solve() {cin>>n;for(int i=1;i<=n;i++) cin>>a[i];int ans=0;for(int k=1;k<=n;k++){//枚举kif(n%k==0){int tmp=0;for(int i=1;i+k<=n;i++){tmp=gcd(tmp,abs(a[i+k]-a[i]));}if(tmp>=2||tmp==0) ans++;}}cout<<ans<<endl;
}
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--) {solve();}return 0;
}相关文章:

Codeforces Round 919 (Div. 2)
Problem - A - Codeforces n个约束条件 a x 求出满足n个约束条件的整数的个数 大于等于x,取最大的 小于等于x,取最小的 然后不等于x的,记录在区间范围内的个数,减去这些 #include<bits/stdc.h> #define endl \n #define …...

面向经验丰富的开发人员的最佳 Linux 发行版
在深入研究最佳 Linux 发行版之前,让我们回顾一下历史。到 2021 年,Linux 操作系统已经有 30 年的历史了,从作为开发者 Linus Torvalds 的个人项目开始,它已经走过了很长一段路。最初发布时,其源代码被分发给用户&…...

Rust-借用检查
Rust语言的核心特点是:在没有放弃对内存的直接控制力的情况下,实现了内存安全。 所谓对内存的直接控制能力,前文已经有所展示:可以自行决定内存布局,包括在栈上分配内存,还是在堆上分配内存;支…...
xcode安装及运行源码
抖音教学视频 目录 1、xcode 介绍 2、xcode 下载 3、xocde 运行ios源码 4、快捷键 1、xcode 介绍 Xcode 是运行在操作系统Mac OS X上的集成开发工具(IDE),由Apple Inc开发。Xcode是开发 macOS 和 iOS 应用程序的最快捷的方式。Xcode 具有…...

x-cmd pkg | czg - git commit 智能生成工具
目录 简介首次用户功能特点竞品和相关作品进一步探索 简介 czg 源于 commitizen/cz-cli 交互插件中 cz-git 的延伸项目,重新使用 TypeScript 编写的零依赖独立的 Node.js 命令行工具。旨在使用交互友好的方式,辅助用户生成规范的 git commit message 约…...

Go的并发练习题目
经典并发题目 现在有4个协程,分别对应编号为1,2,3,4,每秒钟就有一个协程打印自己的编号,要求编写一个程序,让输出的编号总是按照1,2,3,4,1,2,3,4这样的规律一直打印下去 type Token struct { }func newWorker(id int, ch chan Token, nextC…...
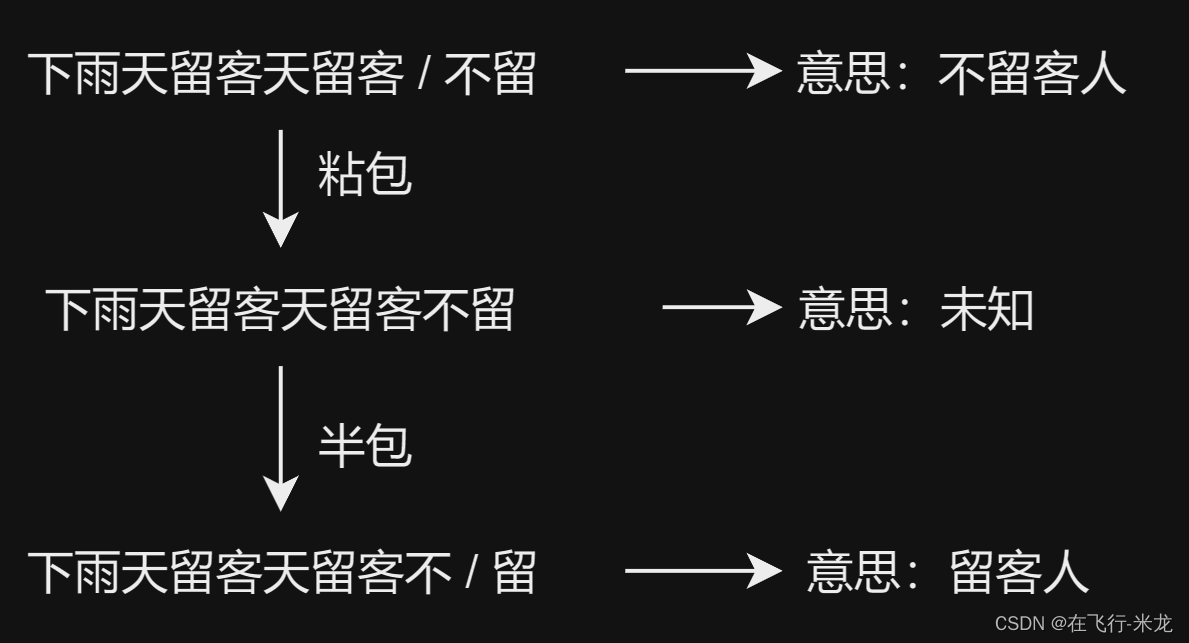
Python 网络编程之粘包问题
【一】粘包问题介绍 【1】粘包和半包 粘包: 定义: 粘包指的是发送方发送的若干个小数据包被接收方一次性接收,形成一个大的数据包。原因: 通常是因为网络底层对数据传输的优化,将多个小数据包组合成一个大的数据块一次…...
旧衣回收小程序搭建:降低企业成本,提高回收效率!
在人们环保意识提升下,旧衣回收行业受到了大众的关注,同时旧衣回收具有门槛低、利润大的优势。在我国,回收行业不仅帮助普通人就业获利,还对环保做出了较大贡献。因此,旧衣回收行业成为了当下的热门商业模式࿰…...
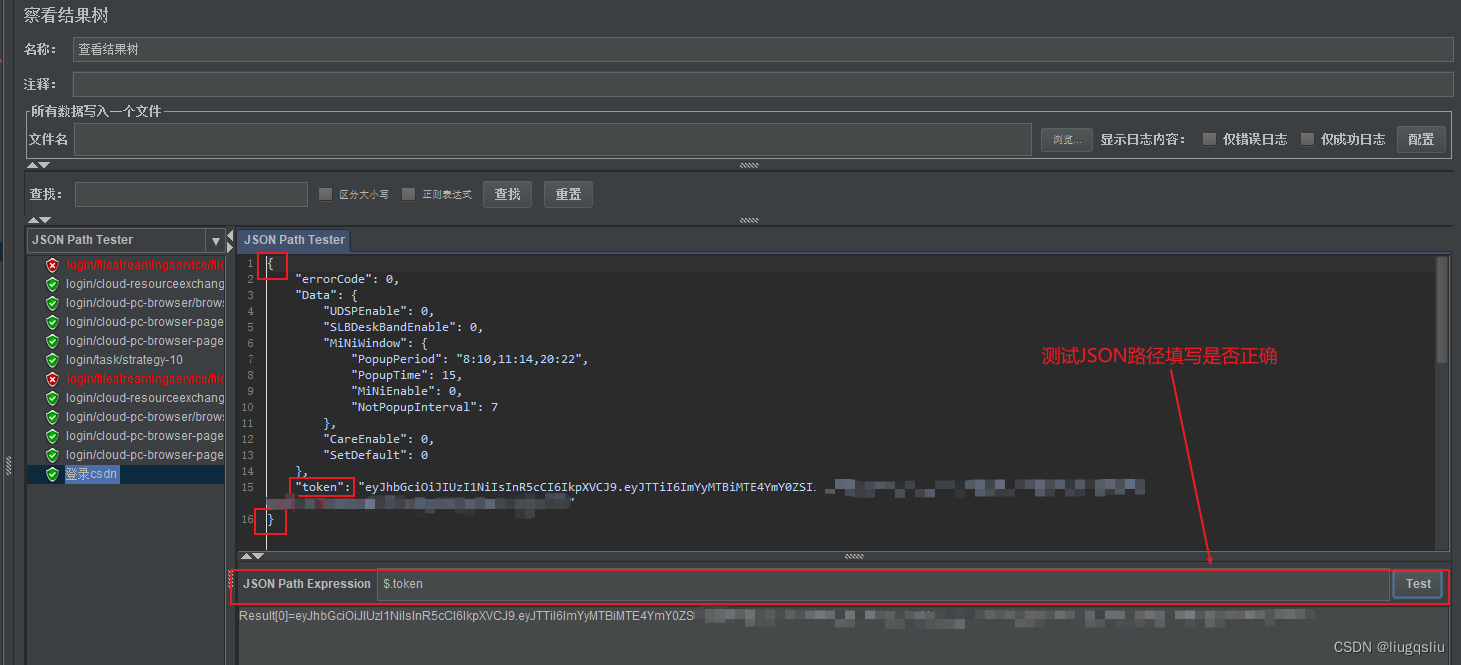
Jmeter后置处理器——JSON提取器
目录 1、简介 2、使用步骤 1)添加线程组 2)添加http请求 3) 添加JSON提取器 1、简介 JSON是一种简单的数据交换格式,允许互联网应用程序快速传输数据。JSON提取器可以从JSON格式响应数据中提取数据、简化从JSON原始数据中提取特定…...

[SWPUCTF 2022 新生赛]奇妙的MD5
[SWPUCTF 2022 新生赛]奇妙的MD5 wp 题目页面: 提示:可曾听过ctf 中一个奇妙的字符串。 奇妙的字符串 奇妙的字符串,又跟 MD5 有关,我只知道两个: 一个是 MD5 加密后弱比较等于自身,这个字符串是 0e215…...

MHFormer 论文解读
目录 Multi-Hypothesis Transformer 结果 Introduction & Related work 多假设 为什么作者提出这个模型? 3.Multi-Hypothesis Transformer 3.1 Preliminary 3.2 MultiHypothesis Generation 3.3 Temporal Embedding 3.4. SelfHypothesi…...
函数使用详解)
Python列表append()函数使用详解
在Python中,列表是一种可变序列类型,可以用来存储多个元素。列表的append()函数是用于在列表末尾添加新元素的内置方法。本文将详细介绍Python列表的append()函数及其使用方法。 一、append()函数的基本语法 append()函数的语法非常简单,只…...
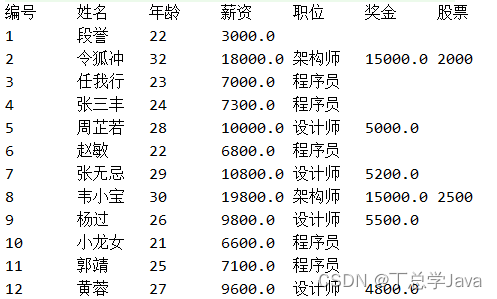
第08章_面向对象编程(高级)拓展练习(关键字:static,代码块,关键字:final,抽象类和抽象方法,接口,内部类,枚举类,注解,包装类)
文章目录 第08章_面向对象编程(高级)拓展练习01-关键字:static1、银行账户类2、图形类3、数组工具类4、二分查找5、二分查找6、素数7、阅读代码,分析运行结果8、阅读代码,分析运行结果 02-代码块9、阅读代码࿰…...

分布式光伏运维平台在提高光伏电站发电效率解决方案
摘要:伴随着能源危机和环境恶化问题的日益加重,科技工作者进一步加大对新能源的开发和利用。太阳能光伏发电作为新型清洁能源的主力军,在实际生产生活中得到了广泛的应用。然而,光伏发电效率偏低,成为制约光伏发电发展…...
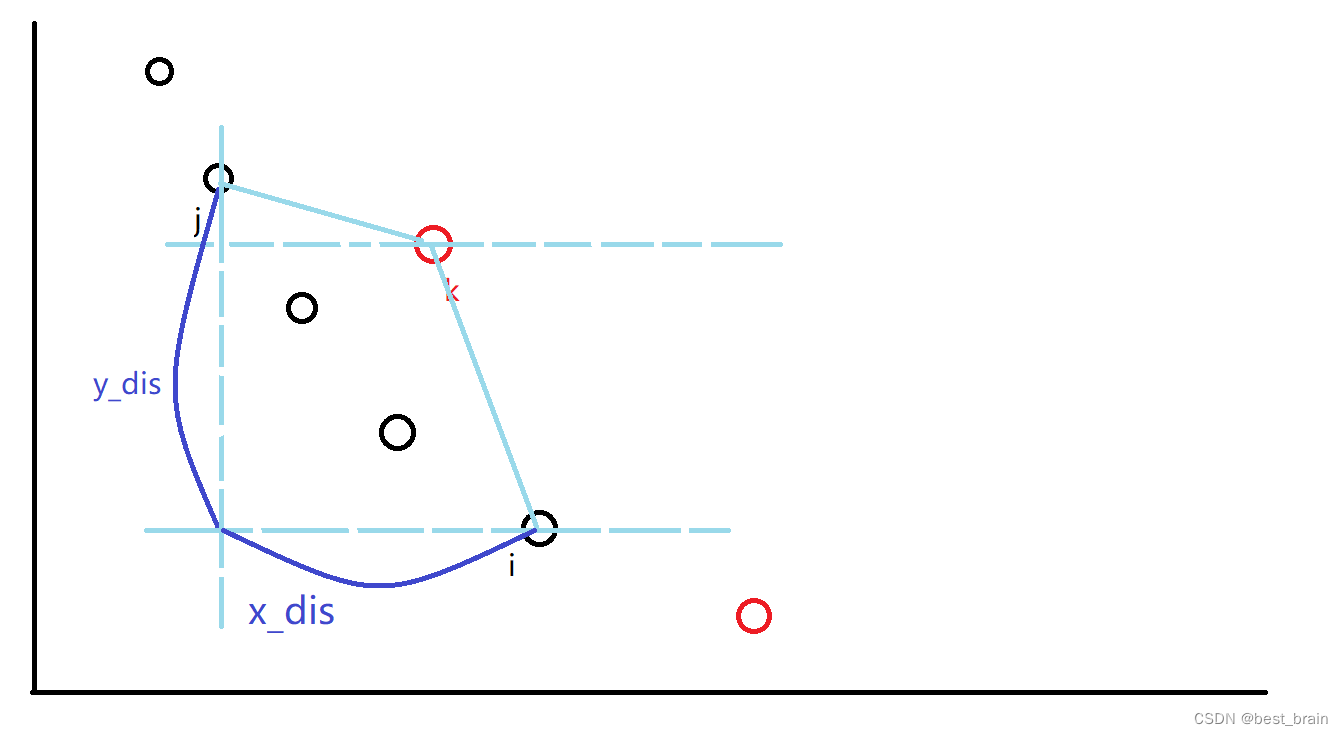
2024.1.14~1.20 周内刷题总结
2024.1.14~1.20 周内刷题总结 [ABC158F] Removing Robots 题解[ABC145F] Laminate 题解[ABC254G] Elevators 题解(坑点总结)[ARC160C] Power Up 题解[ABC203F] Weed 题解Shopping时代的眼泪 [ABC158F] Removing Robots 题解 \qquad 题面 \qquad 本题的连…...

徐州数字孪生元宇宙赋能工业智能制造,助力传统制造业数字化转型
徐州数字孪生元宇宙赋能工业智能制造,助力传统制造业数字化转型。在徐州市制造业企业数字化转型的过程中,数字孪生技术的应用已经取得了显著成效。一方面,企业的生产效率得到了显著提高,产品质量也得到了有效保障。另一方面&#…...

智云谷再获资本市场青睐,完成数千万元A+轮融资
近日,深圳前海智云谷科技有限公司(以下简称“智云谷”)完成数千万元A轮融资,本轮融资由青松基金独家投资,多维资本担任独家融资财务顾问。本轮融资资金将用于扩大新技术研发投入、智能工厂扩产、加速产品交付ÿ…...
| 文章顶部信息(Top matter))Part 1)
ACM论文LaTeX模板解析(三)| 文章顶部信息(Top matter))Part 1
本文收录于专栏:ACM 论文 LaTeX模板解析,本专栏将会围绕ACM 论文 LaTeX模板解析持续更新。欢迎点赞收藏关注! 文章目录 有许多命令可以设置文章的顶部信息或(计算机科学术语)元数据。它们建立了出版物名称、文章标题、…...

[GDOUCTF 2023]受不了一点
[GDOUCTF 2023]受不了一点 wp 题目代码: <?php error_reporting(0); header("Content-type:text/html;charsetutf-8"); if(isset($_POST[gdou])&&isset($_POST[ctf])){$b$_POST[ctf];$a$_POST[gdou];if($_POST[gdou]!$_POST[ctf] &&…...

精心挑选免费好用的api,推荐给大家
企业基本信息:通过公司名称/公司ID/注册号或社会统一信用代码获取企业基本信息,企业基本信息包括公司名称或ID、类型、成立日期、经营状态、注册资本、法人、工商注册号、统一社会信用代码、组织机构代码、纳税人识别号等字段信息。 AI绘画-Stable Diff…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
