红黑树(RBTree)
目录
一、红黑树简介
二、红黑树的来源
三、什么是红黑树
四、红黑树的性质
五、红黑树的节点定义
六、红黑树的操作
6.1、红黑树的查找
6.2、红黑树的插入
七、红黑树的验证
八、红黑树和AVL树的比较
一、红黑树简介
红黑树是一种自平衡的二叉查找树,是一种高效的查找树。它是由 Rudolf Bayer 于1978年发明,在当时被称为平衡二叉 B 树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的红黑树。红黑树具有良好的效率,它可在 O(logN) 时间内完成查找、增加、删除等操作。
二、红黑树的来源
对于二叉搜索树,如果插入的数据是随机的,那么它就是接近平衡的二叉树,平衡的二叉树,它的操作效率(查询,插入,删除)效率较高,时间复杂度是O(logN)。但是可能会出现一种极端的情况,那就是插入的数据是有序的(递增或者递减),那么所有的节点都会在根节点的右侧或左侧,此时,二叉搜索树就变为了一个链表,它的操作效率就降低了,时间复杂度为O(N),所以可以认为二叉搜索树的时间复杂度介于O(logN)和O(N)之间,视情况而定。那么为了应对这种极端情况,红黑树就出现了,它是具备了某些特性的二叉搜索树,能解决非平衡树问题,红黑树是一种接近平衡的二叉树(说它是接近平衡因为它并没有像AVL树的平衡因子的概念,它只是靠着满足红黑节点的5条性质来维持一种接近平衡的结构,进而提升整体的性能,并没有严格的卡定某个平衡因子来维持绝对平衡)。
三、什么是红黑树
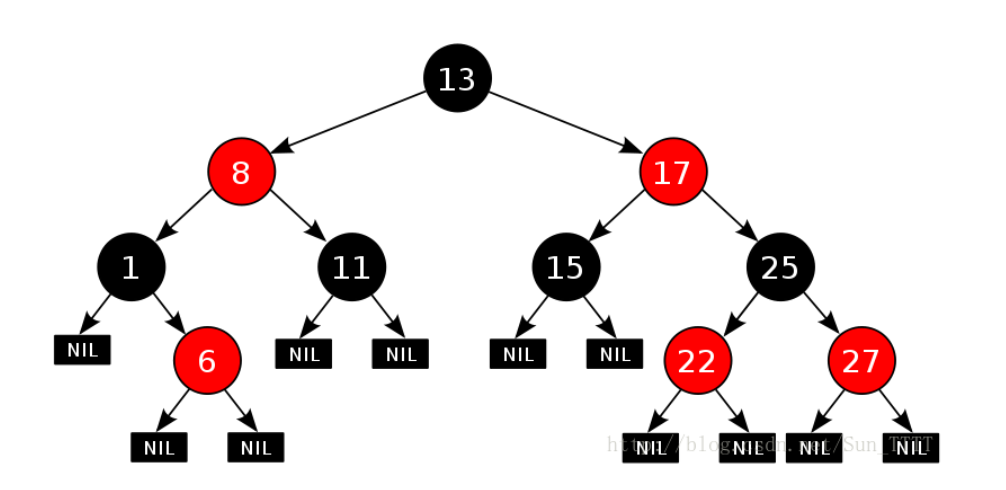
四、红黑树的性质
五、红黑树的节点定义
enum Colour
{RED,BLACK,
};template<class T>
struct RBTreeNode
{RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;T _data;Colour _col;RBTreeNode(const T& data):_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _col(RED){}
};这里我们默认节点的颜色是红色:
新插入的节点默认为红色,有利于保持红黑树的平衡性质。当插入一个新节点时,由于新节点默认为红色,可以避免破坏红黑树的规则,从而简化了插入操作后的平衡调整。同时,将新节点默认为红色也有助于降低平衡调整的复杂度,使得红黑树的插入和删除操作更加高效。
六、红黑树的操作
红黑树的基本操作和其他树形结构一样,一般都包括查找、插入、删除等操作。前面说到,红黑树是一种自平衡的二叉查找树,既然是二叉查找树的一种,那么查找过程和二叉查找树一样,比较简单,这里不再赘述。相对于查找操作,红黑树的插入和删除操作就要复杂的多。尤其是删除操作,要处理的情况比较多,下面就来分情况讲解。
6.1、红黑树的查找
Node* Find(const K& key){Node* cur = _root;KeyOfT kot;while (cur){if (kot(cur->_data) < key){cur = cur->_right;}else if (kot(cur->_data) > key){cur = cur->_left;}else{return cur;}}return nullptr;}6.2、红黑树的插入
- parent:父节点
- sibling:兄弟节点
- uncle:叔父节点( parent 的兄弟节点)
- grand:祖父节点( parent 的父节点)
红黑树的插入过程和二叉查找树插入过程基本类似,不同的地方在于,红黑树插入新节点后,需要进行调整,以满足红黑树的性质。
红黑树节点的颜色要么是红色要么是黑色,那么在插入新节点时,这个节点应该是红色,原因也不难理解。如果插入的节点是黑色,那么这个节点所在路径比其他路径多出一个黑色节点,这个调整起来会比较麻烦(参考红黑树的删除操作,就知道为啥多一个或少一个黑色节点时,调整起来这么麻烦了)。如果插入的节点是红色,此时所有路径上的黑色节点数量不变,仅可能会出现两个连续的红色节点的情况。这种情况下,通过变色和旋转进行调整即可,比之前的简单多了。所以插入的时候将节点设置为红色,可以保证满足性质 1、2、4、5 ,只有性质3不一定满足,需要进行相关调整。如果是添加根节点,则将节点设定为黑色。
情况一、 cur为红,p为红,g为黑,u存在且为红
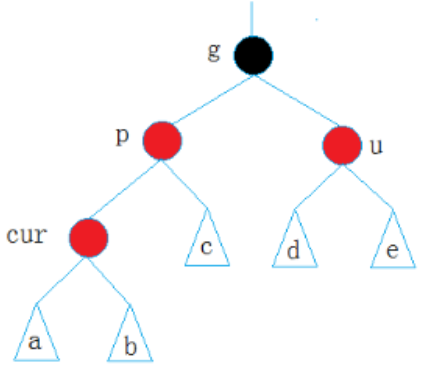
解决方法:将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。
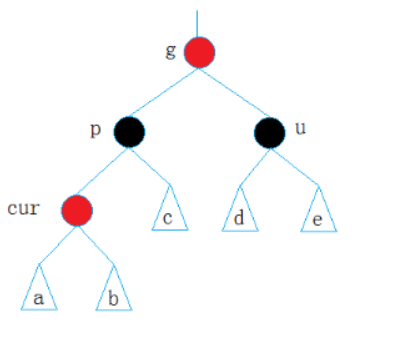
如果g是根节点,调整完成后,需要将g改成黑色;
如果g是子树,g一定有双亲,且g的双亲如果是红色,需要继续向上调整,否则不用。
情况二、cur为红,p为红,g为黑,u不存在 / u存在且为黑
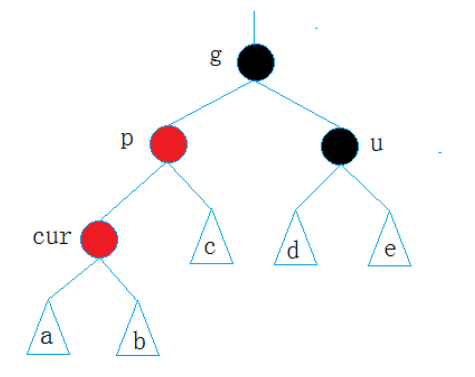

解决方法:
-
如果p为g的左孩子,cur为p的左孩子,则进行右单旋转,p变黑,g变红
-
如果p为g的右孩子,cur为p的右孩子,则进行左单旋转,p变黑,g变红
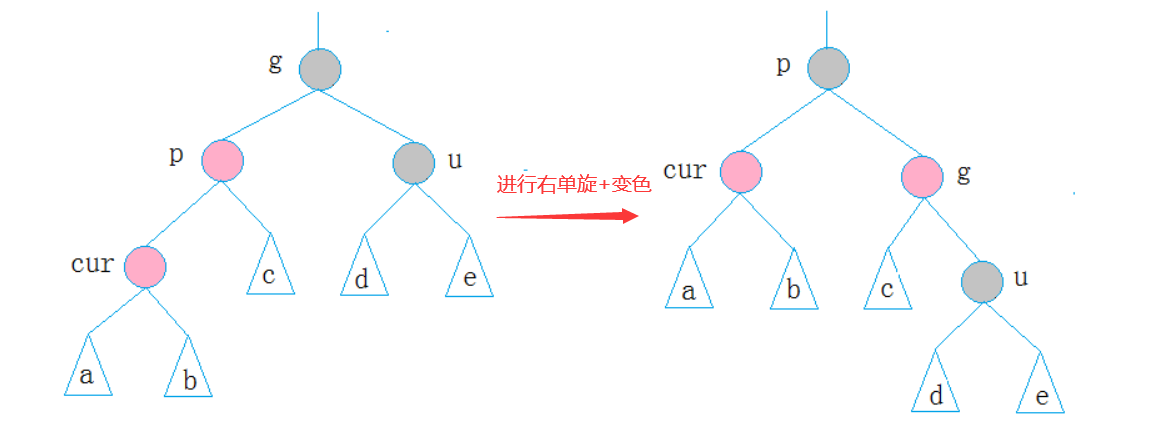
情况三: cur为红,p为红,g为黑,u不存在/u存在且为黑

和情况而类似,只不过情况而是单旋,情况三单旋解决不了问题,所以要双旋。
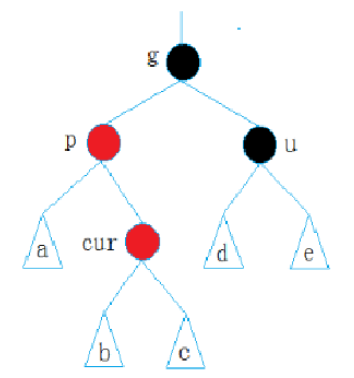
解决方法:
-
如果p为g的左孩子,cur为p的右孩子,则针对p做左单旋转,p旋转后再对g进行右单旋,旋转后将cur变黑,g变红
-
如果p为g的右孩子,cur为p的左孩子,则针对p做右单旋转,p旋转后再对g进行左单旋,旋转后将cur变黑,g变红
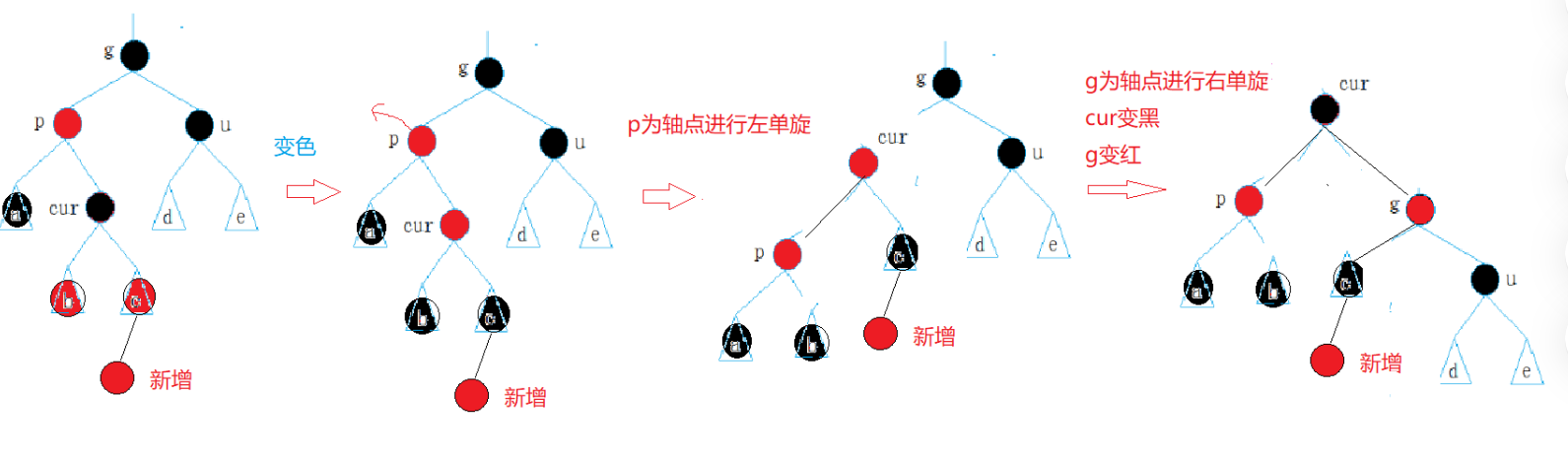
插入函数的实现:
bool Insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return true;}KeyOfT kot;Node* parent = nullptr;Node* cur = _root;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(data);if (kot(parent->_data) > kot(data)){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (grandfather->_left == parent){Node* uncle = grandfather->_right;// 情况1:u存在且为红,变色处理,并继续往上处理if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 继续往上调整cur = grandfather;parent = cur->_parent;}else // 情况2+3:u不存在/u存在且为黑,旋转+变色{// g// p u// c if (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p u// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;//parent->_col = RED;grandfather->_col = RED;}break;}}else // (grandfather->_right == parent){// g// u p// cNode* uncle = grandfather->_left;// 情况1:u存在且为红,变色处理,并继续往上处理if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 继续往上调整cur = grandfather;parent = cur->_parent;}else // 情况2+3:u不存在/u存在且为黑,旋转+变色{// g// u p// cif (cur == parent->_right){RotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{// g// u p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}旋转代码实现:
void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppnode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppnode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppnode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}}
七、红黑树的验证
bool IsRBTree()
{//空树if (_root == nullptr){return true;}//根节点为黑色if (_root->_col == RED){cout << "根节点为红色" << endl;return false;}//黑色结点数量各路径上相同//先走一条得到基准值int Blacknum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)Blacknum++;cur = cur->_left;}//检查子树int i = 0;return _IsRBTree(_root, Blacknum, i);
}bool _IsRBTree(Node* root, int blacknum, int count)
{//递归到空节点if (root == nullptr){if (blacknum == count)return true;cout << "各路径上黑色节点个数不同" << endl;return false;}//子节点为红则检查父节点是否为红(通过父节点检查子节点会遇到空节点)if (root->_col == RED && root->_parent->_col == RED){cout << "存在连续红色节点" << endl;return false;}//计数黑结点if (root->_col == BLACK)count++;//递归左右子树return _IsRBTree(root->_left, blacknum, count) && _IsRBTree(root->_right, blacknum, count);
}
八、红黑树和AVL树的比较
- AVL树的时间复杂度虽然优于红黑树,但是对于现在的计算机,cpu太快,可以忽略性能差异
- 红黑树的插入删除比AVL树更便于控制操作
- 红黑树整体性能略优于AVL树(红黑树旋转情况少于AVL树)
相关文章:

红黑树(RBTree)
目录 一、红黑树简介 二、红黑树的来源 三、什么是红黑树 四、红黑树的性质 五、红黑树的节点定义 六、红黑树的操作 6.1、红黑树的查找 6.2、红黑树的插入 七、红黑树的验证 八、红黑树和AVL树的比较 一、红黑树简介 红黑树是一种自平衡的二叉查找树…...
训练YOLOS-S
文章目录 1 数据处理2 配置训练参数3 可能会遇到的报错 1 数据处理 修改类别数:在models/detector.py中定位到def build(args):,将num_classes进行修改,改为最大的类别id1。我有4个类别,类别id是从0~3,因此max_id3&am…...

集成SpringCloudAlibaba短信服务 短信验证码
1.1 SpringCloudAlibaba短信服务简介 短信服务(Short Message Service)是阿里云为用户提供的一种通信服务的能力。 产品优势:覆盖全面、高并发处理、消息堆积处理、开发管理简单、智能监控调度 产品功能:短信通知、短信验证码、…...

存储卷(数据卷)—主要是nfs方式挂载
1、定义 容器内的目录和宿主机的目录进行挂载 容器在系统上的生命周期是短暂的,一旦容器被删除,数据会丢失。k8s基于控制器创建的pod,delete相当于重启,容器的状态会恢复到原始状态。一旦回到原始状态,后天编辑的文件…...
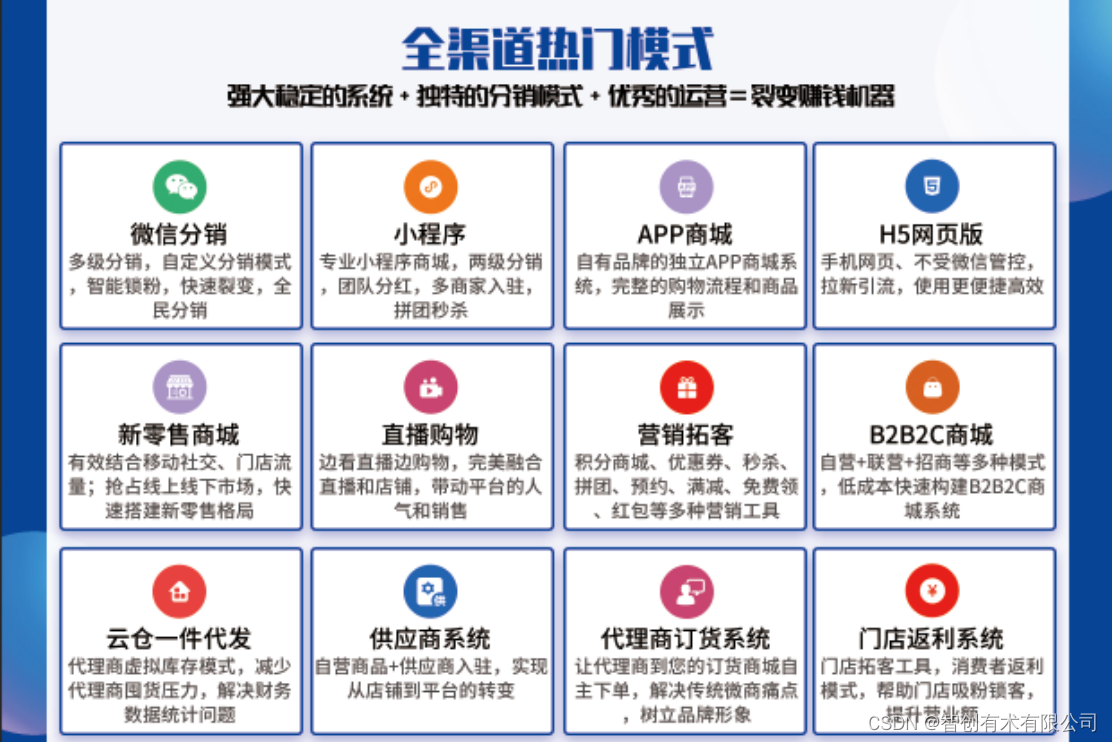
城市酷选模式开发(门店免单排队返利系统)
城市酷选模式开发(门店免单排队返利系统)【阿巴】城市酷选商城开发免单排队返利小程序搭建、城市酷选模式开发、城市酷选系统商城开发、城市酷选APP系统开发、城市酷选 每经AI快讯,有投资者在投资者互动平台提问:“以塑代钢”已成…...
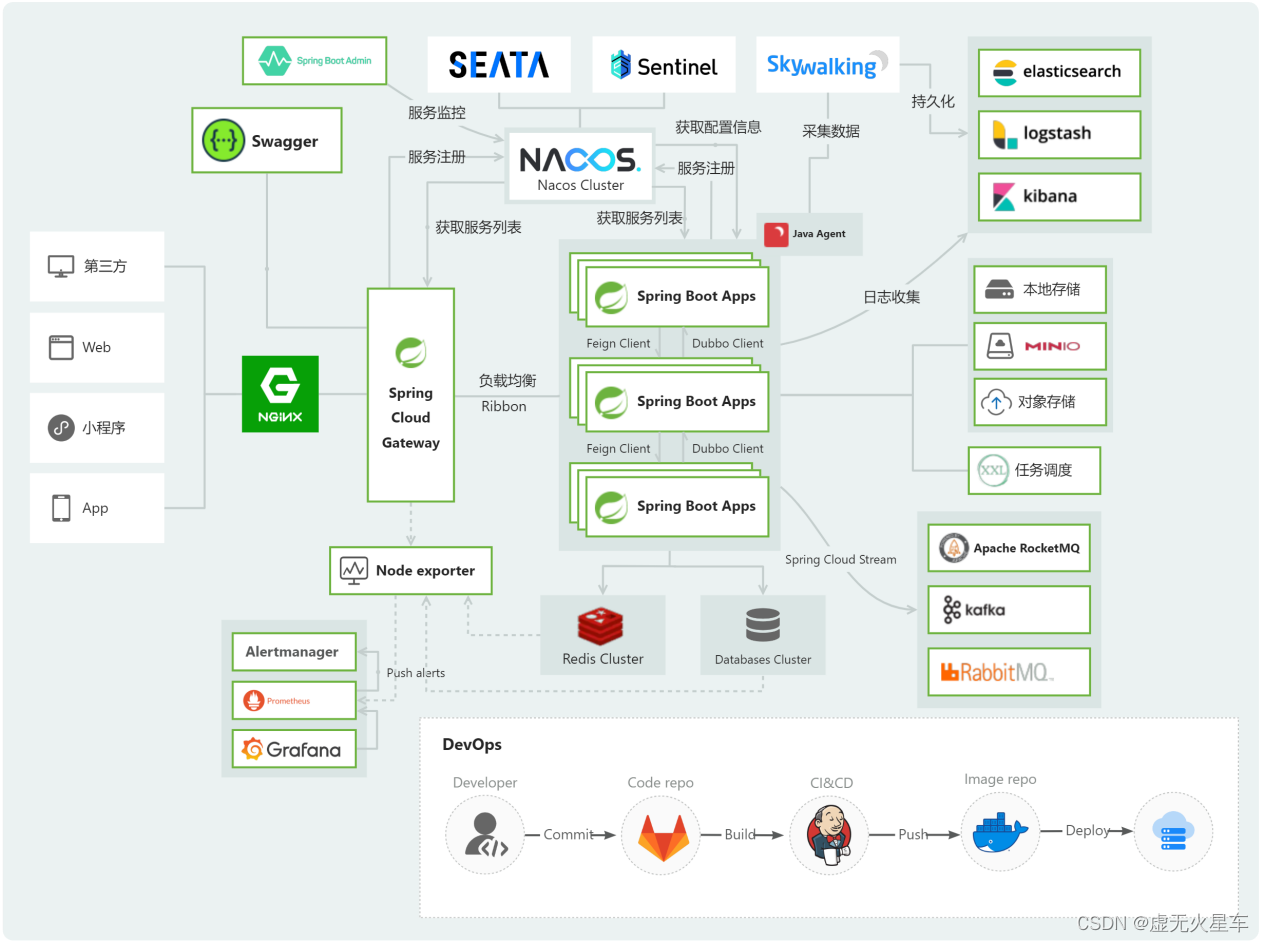
JNPF低代码引擎到底是什么?
最近听说一款可以免费部署本地进行试用的低代码引擎,源码上支持100%源码,提供的功能和技术支持比较完善。借助这篇篇幅我们了解下JNPF到底是什么? JNPF开发平台是一款PaaS服务为核心的零代码开发平台,平台提供了多租户账号管理、主…...

#基础#使用Jupyter进行Notebook的转换 .ipynb文件导出为.md文件
我们在使用jupyter 写代码后,经常遇到一些写完想把文件转成markdown格式的场景,这里就教你怎么处理相关的问题 使用Jupyter进行Notebook的转换 .ipynb文件导出为.md文件 pip install nbconvert pip install pandoc jupyter nbconvert --to markdown 文…...

工信部颁发的人工智能证书《自然语言与语音处理设计开发工程师》证书到手啦!
工信部颁发的人工智能证书《自然语言与语音处理设计开发工程师》证书拿到手啦! 近期正在报考的工信部颁发的人工智能证书还有: 《计算机视觉处理设计开发工程师》中级 2024年1月24日至28日-北京 《自然语言与语音处理设计开发工程师》中级 第二期 20…...

canvasdrawer 微信原生小程序生成海报图片
在小程序中生成海报是一种非常有效的推广方式 用户可以使用小程序的过程中生成小程序海报并分享给他人 通过海报的形式,用户可以直观地了解产品或服务的特点和优势 常见绘制海报方式 目前,小程序海报有两种常见的实现方式: canvas 绘制…...

linux基础学习(3):挂载
挂载可以理解为给磁盘空间一个可访问的入口,那个入口称为挂载点,相当于windows中的盘符。 1.挂载命令mount 1.1直接输入mount 查看系统已挂载的设备 1.2挂载与卸载命令 mount -t 文件系统名 设备文件名 挂载点 | umount 挂载点 或 umount 设…...

[每周一更]-(第82期):认识自然处理语言(NLP)
GPT的大火,带起了行业内大模型的爆发;国内外都开始拥有或者研发自己的大模型,下边我们从NLP来进一步深入了解大模型、AI。 一、什么是NLP? 自然语言处理(英语:Natural Language Processing,缩…...

Win11如何设置时间显示秒
1、打开注册表 计算机\HKEY_CURRENT_USER\Software\Microsoft\Windows\CurrentVersion\Explorer\Advanced 2、进入以上路径 Advanced新建dword32位,新建一个文件,设置一个名称 3、修改之前创建的文件 4、重启电脑...

世界人口数据分析与探索
文章目录 世界人口数据集介绍数据集 1:世界国家统计数据:数据集 2:世界人口详细信息(2023 年):数据集 3:按年份划分的世界人口(1950-2023): 数据分析导入必要…...

自动驾驶的未来:BEV与Occupancy网络全景解析与实战揭秘!
自动驾驶领域中,什么是BEV?什么是Occupancy? 作者:小柠檬 | 来源:公众号「3DCV」 BEV是Bird’s Eye View 的缩写,意为鸟瞰视图。在自动驾驶领域,BEV 是指从车辆上方俯瞰的场景视图。BEV 图像可以…...

大众点评评论采集软件使用教程
导出字段: 店铺ID 评论ID 发布时间 人均消费 评分 详情链接 点赞数 浏览数 评论数 最后更新时间 发布平台 推荐 评论详情 原始评论 图片数 图片链接 用户等级 用户名称 用户头像 VIP 私...

2024年前端面试中JavaScript的30个高频面试题之中级知识
基础知识 高级知识 13. 什么是闭包?闭包的用例有哪些? 闭包是一个功能,它允许函数捕获定义该函数的环境(或保留对作用域中变量的访问)即使在该作用域已经关闭后。 我们可以说闭包是函数和词法环境的组合,其中定义了该函数。 换句话说,闭包为函数提供了访问自己的作用域、…...
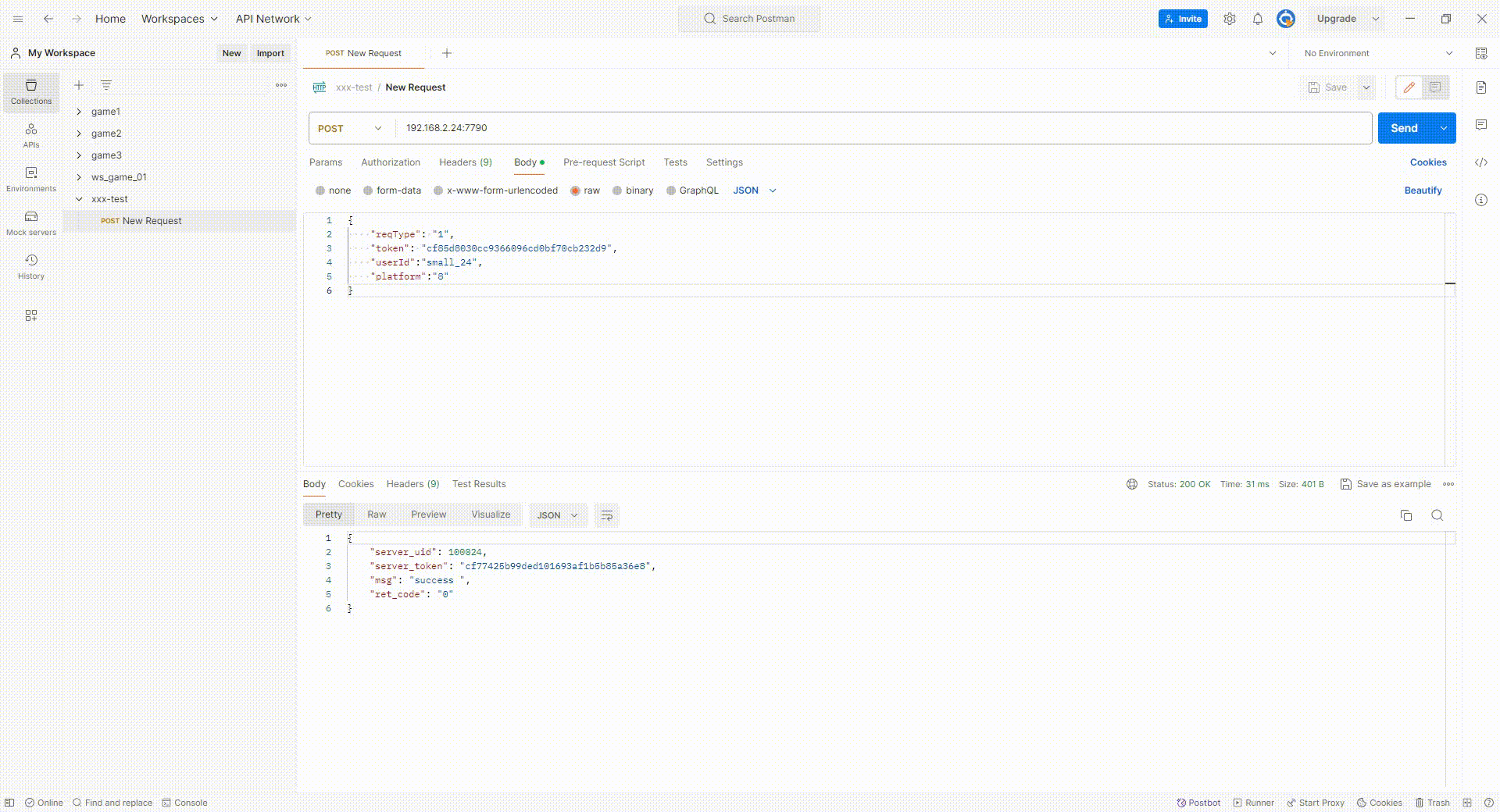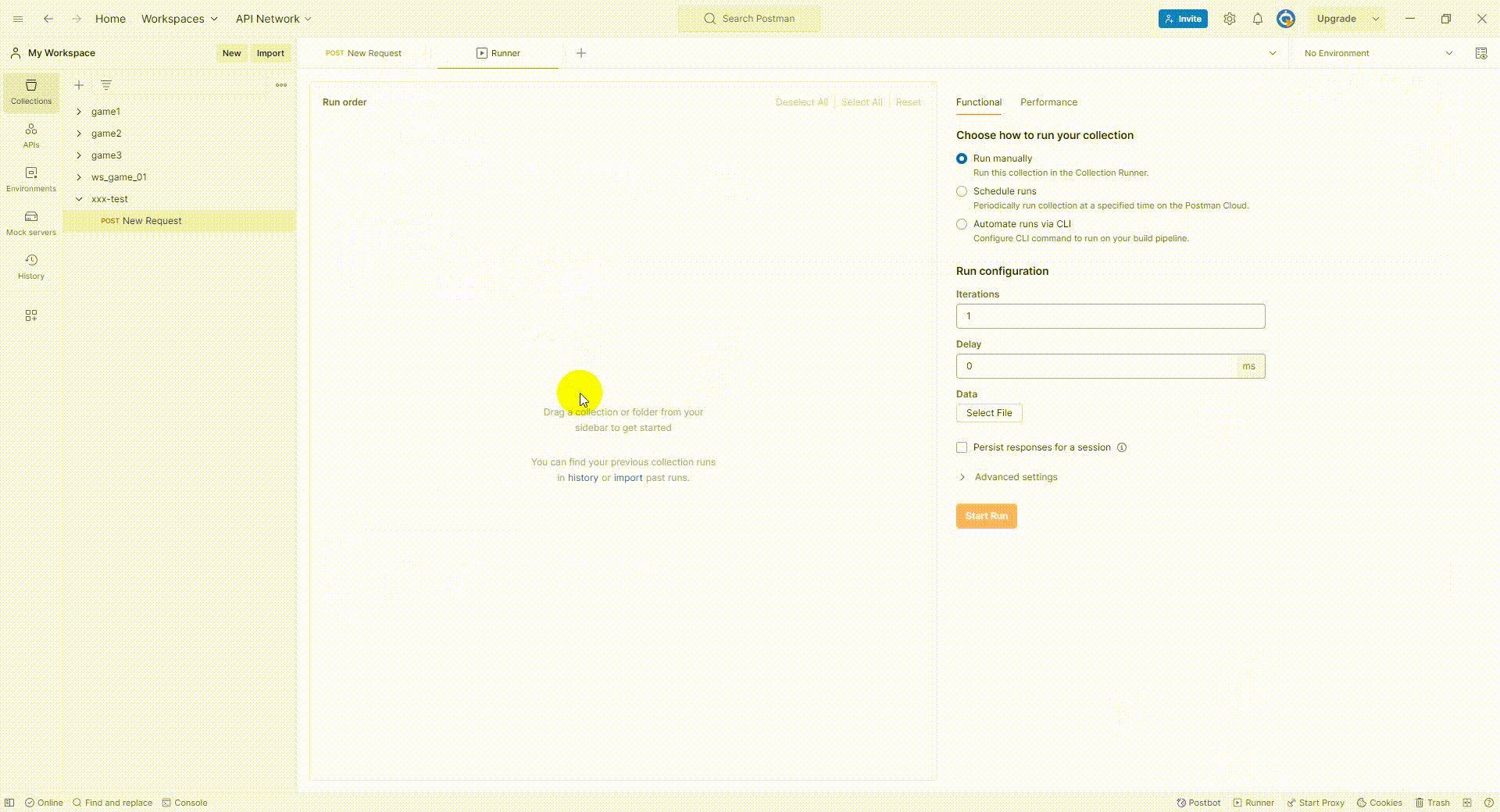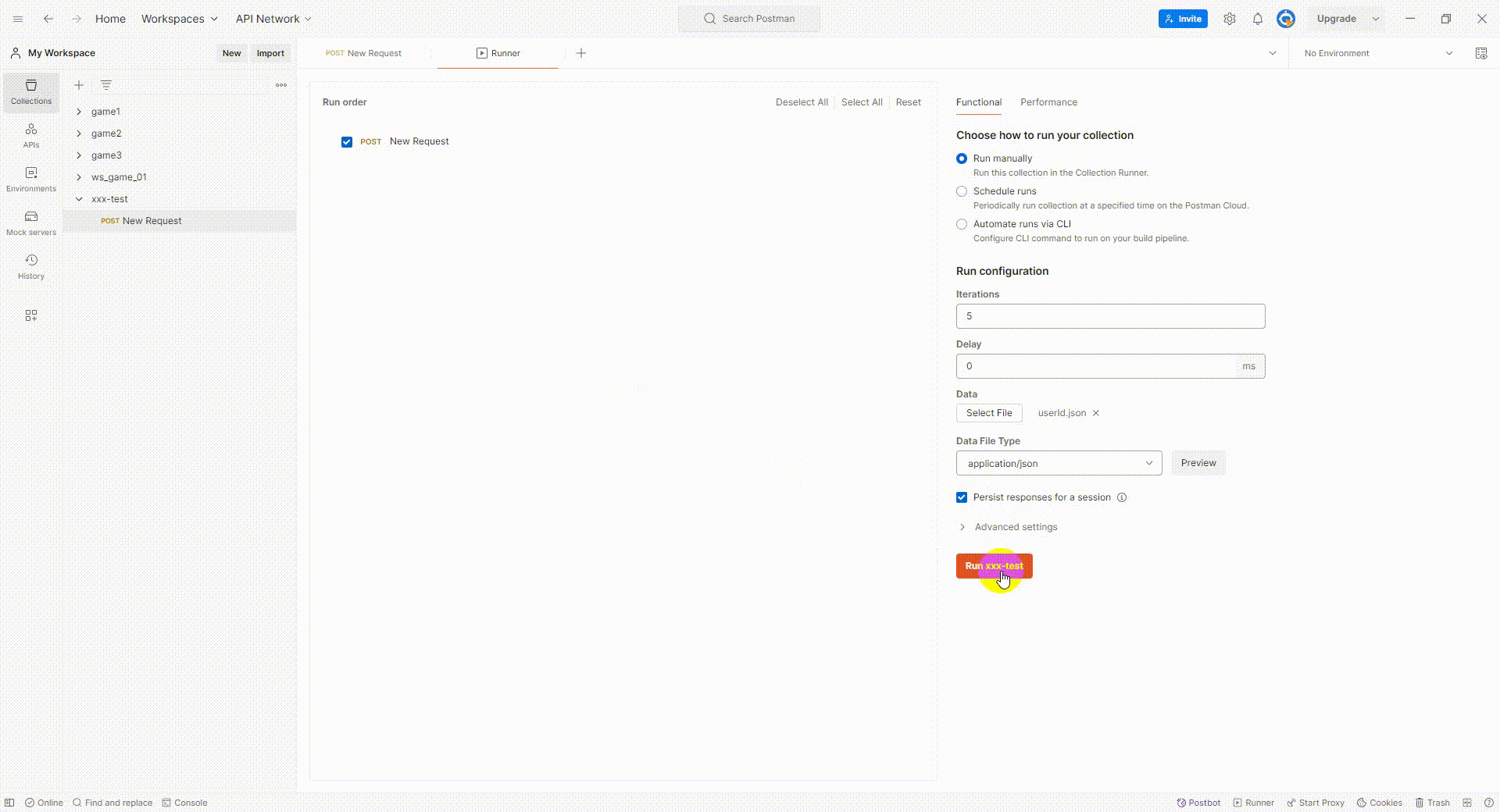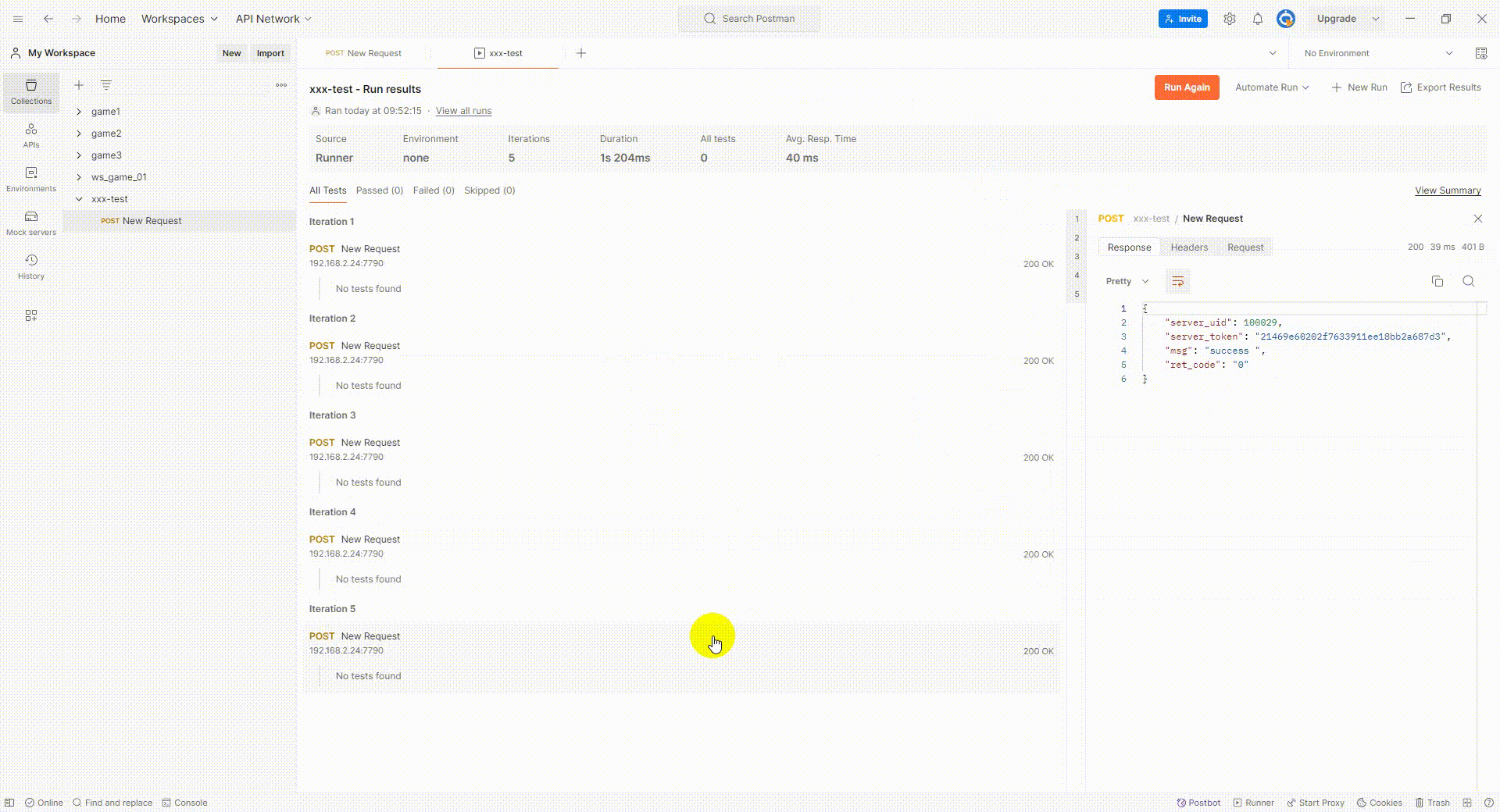
postman 简单测试(一)
1.postman官网 Postman API Platform 2.研究了一下postman 一些简单的功能,自己做个记录,同时希望能节约点测试时间。 2.1新建一个 collections 长期测的话,最好注册一个账号,开放更多功能。 2.2新建一个请求 后端要先搭建起来…...

12.1、2、3-同步状态机的结构以及Mealy和Moore状态机的区别
同步状态机的结构以及Mealy和Moore状态机的区别 1,介绍Mealy型状态机和Moore型状态机的两种结构2,设计高速电路的方法 由于寄存器传输级(RTL)描述的是以时序逻辑抽象所得到的有限状态机为依据,因此,把一个时…...
前端框架前置课Node.js学习(1) fs,path,模块化,CommonJS标准,ECMAScript标准,包
目录 什么是Node.js 定义 作用: 什么是前端工程化 Node.js为何能执行Js fs模块-读写文件 模块 语法: 1.加载fs模块对象 2.写入文件内容 3.读取文件内容 Path模块-路径处理 为什么要使用path模块 语法 URL中的端口号 http模块-创建Web服务 需求 步骤: 案例:浏…...
)
SpringBoot源码启动流程(待完善)
SpringBoot源码启动流程 1. 构造SpringApplication对象 1.1 推测web应用类型 判断关键类是否存在来区分类型 REACTIVENONESERVLET static WebApplicationType deduceFromClasspath() {if (ClassUtils.isPresent(WEBFLUX_INDICATOR_CLASS, null) && !ClassUtils.isP…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
