微信小程序 - 视图与逻辑 介绍
文章目录
- 视图与逻辑
- 一、页面导航
- 1、页面导航 - 声明式导航
- 1.1 导航到tabBar页面
- 1.2 导航到非tabBar页面
- 1.3 后退导航
- 2、页面导航 - 编程式导航
- 2.1 导航到tabBar页面
- 2.2 导航到非tabBar页面
- 2.3 后退导航
- 3、页面导航 - 导航传参
- 3.1 声明式导航传参
- 3.2 编程式导航传参
- 3.3 在 onLoad 中接收导航参数
- 二、页面事件
- 1、页面事件 - 下拉刷新事件
- 1.1 什么是下拉刷新
- 1.2 启用下拉刷新
- 1.3 配置下拉刷新窗口的样式
- 1.4 监听页面的下拉刷新事件
- 1.5 停止下拉刷新的效果
- 2、页面事件 - 上拉触底事件
- 2.1 什么是上拉触底
- 2.2 监听页面的上拉触底事件
- 2.3 配置上拉触底距离
- 三、生命周期
- 1、什么是生命周期
- 2、生命周期的分类
- 3、什么是生命周期函数
- 4、生命周期函数的分类
- 4.1 应用生命周期函数
- 4.2 页面生命周期函数
- 5、应用的生命周期函数
- 6、页面的生命周期函数
- 四、WXS脚本
- 1、WXS 脚本 - 概述
- 1.1 什么是 wxs
- 1.2 wxs 的应用场景
- 1.3 wxs 和 JavaScript 的关系*
- 2、WXS 脚本 - 基础语法
- 2.1 内嵌 wxs 脚本
- 2.2 定义外联的 wxs 脚本
- 2.3 使用外联的 wxs 脚本
- 3、WXS 脚本 - WXS 的特点
- 3.1 与 JavaScript 不同
- 3.2 不能作为组件的事件回调
- 3.3 隔离性
- 3.4 性能好
视图与逻辑
一、页面导航
- 什么是页面导航
在小程序开发中,页面导航是指在不同页面之间进行切换的过程。通过页面导航,用户可以在小程序中流畅地浏览不同的内容和功能模块。
- 小程序中实现页面导航的两种方式
在小程序中,实现页面导航有两种主要方式:声明式导航和编程式导航。
1、页面导航 - 声明式导航
声明式导航是通过在页面的配置中声明导航信息来实现的,开发者只需在页面的配置文件中定义导航相关的信息,小程序框架会自动处理导航逻辑。
1.1 导航到tabBar页面
在声明式导航中,可以通过使用 <navigator> 组件来实现导航到tabBar页面,使用 open-type='switchTab' 来切换到底部导航栏的页面。
<!-- pageA.wxml -->
<navigator url='/pages/tab1/index' open-type='switchTab'>导航到Tab 1页面</navigator>
1.2 导航到非tabBar页面
同样,在声明式导航中,可以使用 <navigator> 组件来导航到非tabBar页面。
<!-- pageB.wxml -->
<navigator url='/pages/otherPage/index'>导航到其他页面</navigator>
1.3 后退导航
声明式导航也支持后退导航,用户可以通过系统的返回按钮或手势返回上一页面。
<!-- pageC.wxml -->
<navigator open-type='navigateBack'>后退导航</navigator>
2、页面导航 - 编程式导航
编程式导航是通过调用小程序框架提供的API来实现页面导航,开发者可以在代码中灵活控制导航逻辑。
2.1 导航到tabBar页面
与声明式导航类似,编程式导航也允许开发者通过调用API导航到tabBar页面。
// pageA.js
wx.switchTab({url: '/pages/tab1/index'
});
2.2 导航到非tabBar页面
编程式导航同样支持导航到非tabBar页面,开发者可以在代码中指定跳转的页面路径。
// pageB.js
wx.navigateTo({url: '/pages/otherPage/index'
});
2.3 后退导航
通过编程式导航,开发者可以实现更精细的后退导航控制,例如在特定条件下执行后退操作。
// pageC.js
wx.navigateBack({delta: 1
});
3、页面导航 - 导航传参
在开发过程中,有时候需要在不同页面之间传递参数。页面导航支持导航传参,分为声明式导航和编程式导航两种方式。
3.1 声明式导航传参
通过在页面路径中配置参数,实现声明式导航时可以传递参数给目标页面。
<!-- pageD.wxml -->
<navigator url='/pages/paramPage/index?param1=value1¶m2=value2'>带参数导航</navigator>
3.2 编程式导航传参
在编程式导航中,开发者可以通过API调用传递参数给目标页面。
// pageE.js
wx.navigateTo({url: '/pages/paramPage/index?param1=value1¶m2=value2'
});
3.3 在 onLoad 中接收导航参数
在目标页面的 onLoad 生命周期中,可以通过获取参数对象来获取传递过来的导航参数。
// paramPage.js
Page({onLoad: function(options) {console.log(options.param1); // 输出: value1console.log(options.param2); // 输出: value2}
});
以上是关于小程序中页面导航的基本介绍,下一节将深入讨论页面事件的处理方式。
二、页面事件
1、页面事件 - 下拉刷新事件
1.1 什么是下拉刷新
下拉刷新是一种用户在页面顶部向下滑动时触发的事件,通常用于实现页面的数据更新或重新加载。
1.2 启用下拉刷新
要启用下拉刷新功能,需要在页面配置文件中设置 enablePullDownRefresh 为 true。
// pageA.json
{"navigationBarTitleText": "Page A","enablePullDownRefresh": true
}
除了在页面配置中开启全局下拉刷新,还可以在页面中使用 <scroll-view> 组件实现局部的下拉刷新。在 <scroll-view> 组件中设置 bindscrolltoupper 事件监听滚动到顶部时触发的下拉刷新。
<!-- pageB.wxml -->
<scroll-view bindscrolltoupper="onPullDownRefresh" style="height: 100vh;"><!-- 页面内容 -->
</scroll-view>
1.3 配置下拉刷新窗口的样式
可以通过在页面配置中设置 backgroundTextStyle 和 backgroundColor 来配置下拉刷新窗口的样式。
// pageA.json
{"navigationBarTitleText": "Page A","enablePullDownRefresh": true,"backgroundTextStyle": "dark","backgroundColor": "#f8f8f8"
}
1.4 监听页面的下拉刷新事件
在页面的逻辑文件中,通过监听页面的 onPullDownRefresh 事件来监听下拉刷新的操作。
// pageA.js
Page({onPullDownRefresh: function() {// 执行下拉刷新的逻辑console.log("下拉刷新事件触发");}
});
1.5 停止下拉刷新的效果
在下拉刷新的逻辑执行完毕后,需要调用 wx.stopPullDownRefresh() 来停止下拉刷新的效果。
// pageA.js
Page({onPullDownRefresh: function() {// 执行下拉刷新的逻辑console.log("下拉刷新事件触发");// 停止下拉刷新的效果wx.stopPullDownRefresh();}
});
2、页面事件 - 上拉触底事件
2.1 什么是上拉触底
上拉触底是一种用户在页面底部向上滑动时触发的事件,通常用于实现分页加载更多数据。
2.2 监听页面的上拉触底事件
在页面的逻辑文件中,通过监听页面的 onReachBottom 事件来监听上拉触底的操作。
// pageA.js
Page({onReachBottom: function() {// 执行上拉触底的逻辑console.log("上拉触底事件触发");}
});
2.3 配置上拉触底距离
可以通过在页面配置中设置 onReachBottomDistance 来配置上拉触底的距离,即当距离底部指定距离时触发上拉触底事件。
// pageA.json
{"navigationBarTitleText": "Page A","onReachBottomDistance": 50
}
以上是关于小程序中页面事件的详细介绍,全局和局部下拉刷新的使用方式,以及上拉触底事件的监听和配置。下一节将讨论页面的生命周期。
三、生命周期
1、什么是生命周期
生命周期是指一个小程序从被创建到被销毁的整个过程。在这个过程中,小程序会经历不同的阶段和事件,开发者可以通过生命周期函数来执行相应的逻辑操作。
2、生命周期的分类
小程序的生命周期可以分为两类:应用生命周期和页面生命周期。
-
应用生命周期: 小程序整体的生命周期,包括小程序的启动、前台运行、后台运行和销毁。
-
页面生命周期: 单个页面的生命周期,包括页面的加载、显示、初次渲染、再次渲染、隐藏和卸载。
3、什么是生命周期函数
生命周期函数是在特定时机会被自动触发的函数,开发者可以在这些函数中编写相应的逻辑代码。在小程序中,生命周期函数包括应用生命周期函数和页面生命周期函数。
4、生命周期函数的分类
4.1 应用生命周期函数
-
onLaunch(options): 当小程序启动时触发,全局只触发一次。
-
onShow(options): 当小程序进入前台显示状态时触发。
-
onHide(): 当小程序进入后台状态时触发。
4.2 页面生命周期函数
-
onLoad(options): 当页面加载时触发,一次生命周期中只会触发一次。
-
onShow(): 当页面显示时触发。
-
onReady(): 当页面初次渲染完成时触发。
-
onHide(): 当页面隐藏时触发。
-
onUnload(): 当页面卸载时触发。
5、应用的生命周期函数
应用的生命周期函数是指在整个小程序运行过程中会被触发的函数,可以在 app.js 文件中定义。
// app.js
App({onLaunch: function(options) {// 小程序启动时触发},onShow: function(options) {// 小程序进入前台时触发},onHide: function() {// 小程序进入后台时触发}
});
6、页面的生命周期函数
页面的生命周期函数是指在页面加载、显示、渲染和卸载等不同阶段会被触发的函数,可以在每个页面的 pageX.js 文件中定义。
// pageA.js
Page({onLoad: function(options) {// 页面加载时触发},onShow: function() {// 页面显示时触发},onReady: function() {// 页面初次渲染完成时触发},onHide: function() {// 页面隐藏时触发},onUnload: function() {// 页面卸载时触发}
});
以上是关于小程序生命周期的基本介绍,开发者可以根据实际需求在不同的生命周期函数中编写相应的业务逻辑。
四、WXS脚本
1、WXS 脚本 - 概述
1.1 什么是 wxs
WXS(WeiXin Script)是小程序的一种脚本语言,用于在 WXML 中对数据进行逻辑处理。它类似于 JavaScript,但有一些特定的语法和限制。
1.2 wxs 的应用场景
WXS 主要用于处理小程序页面中的逻辑,例如数据的计算、处理字符串等。它可以被用在 WXML 中进行数据绑定和逻辑运算。
1.3 wxs 和 JavaScript 的关系*
WXS 与 JavaScript 有相似之处,但并不完全相同。WXS 主要用于小程序,它的语法和能力受到一些限制,使其更适合于小程序环境下的使用。
2、WXS 脚本 - 基础语法
2.1 内嵌 wxs 脚本
在 WXML 文件中,可以使用 <wxs> 标签来嵌入 wxs 脚本。内嵌的 wxs 脚本可以直接在 WXML 中进行调用。
<!-- pageA.wxml -->
<wxs module="m1">var add = function(a, b) {return a + b;}module.exports.add = add;
</wxs><view>{{ m1.add(1, 2) }}</view>
2.2 定义外联的 wxs 脚本
也可以将 wxs 脚本定义在外部文件,使用 <wxs> 标签的 src 属性引入外联的 wxs 脚本。
<!-- util.wxs -->
var multiply = function(a, b) {return a * b;
}
module.exports.multiply = multiply;<!-- pageB.wxml -->
<wxs src="./util.wxs" module="m2"></wxs><view>{{ m2.multiply(3, 4) }}</view>
2.3 使用外联的 wxs 脚本
外联的 wxs 脚本可以在 WXML 中通过模块的方式调用。
<!-- pageC.wxml -->
<wxs src="/utils/util.wxs" module="m3"></wxs><view>{{ m3.multiply(5, 6) }}</view>
3、WXS 脚本 - WXS 的特点
3.1 与 JavaScript 不同
WXS 在语法和功能上有一些差异,不同于 JavaScript。开发者在使用 WXS 时需注意其特殊的语法和限制。
3.2 不能作为组件的事件回调
WXS 不能作为组件的事件回调函数,不能直接绑定在组件的事件属性上。
3.3 隔离性
WXS 具有独立的作用域,不受页面的其他脚本影响。它的变量和函数不会与页面的 JavaScript 全局作用域发生冲突。
3.4 性能好
由于 WXS 是小程序专用的脚本语言,它在小程序环境下运行更高效,具有较好的性能。
以上是关于 WXS 脚本的基本介绍,开发者可以根据实际需求使用 WXS 在小程序中进行数据处理和逻辑运算。
相关文章:

微信小程序 - 视图与逻辑 介绍
文章目录 视图与逻辑一、页面导航1、页面导航 - 声明式导航1.1 导航到tabBar页面1.2 导航到非tabBar页面1.3 后退导航 2、页面导航 - 编程式导航2.1 导航到tabBar页面2.2 导航到非tabBar页面2.3 后退导航 3、页面导航 - 导航传参3.1 声明式导航传参3.2 编程式导航传参3.3 在 on…...
大创项目推荐 深度学习疫情社交安全距离检测算法 - python opencv cnn
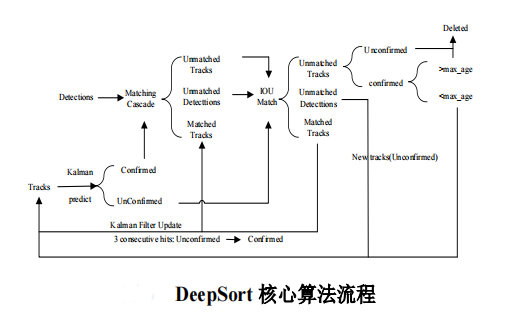
文章目录 0 前言1 课题背景2 实现效果3 相关技术3.1 YOLOV43.2 基于 DeepSort 算法的行人跟踪 4 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **基于深度学习疫情社交安全距离检测算法 ** 该项目较为新颖,适合作为竞赛…...

c语言-库函数strstr()、strtok()、strerror()介绍
文章目录 前言一、库函数strstr()1.1 strstr()介绍1.2 strstr()模拟实现 二、库函数strtok()2.1 strtok()介绍 三、库函数strerror()3.1 strerror()介绍 总结 前言 本篇文章介绍c语言库函数strstr()、strtok()、strerror()的使用。 一、库函数strstr() 1.1 strstr()介绍 str…...
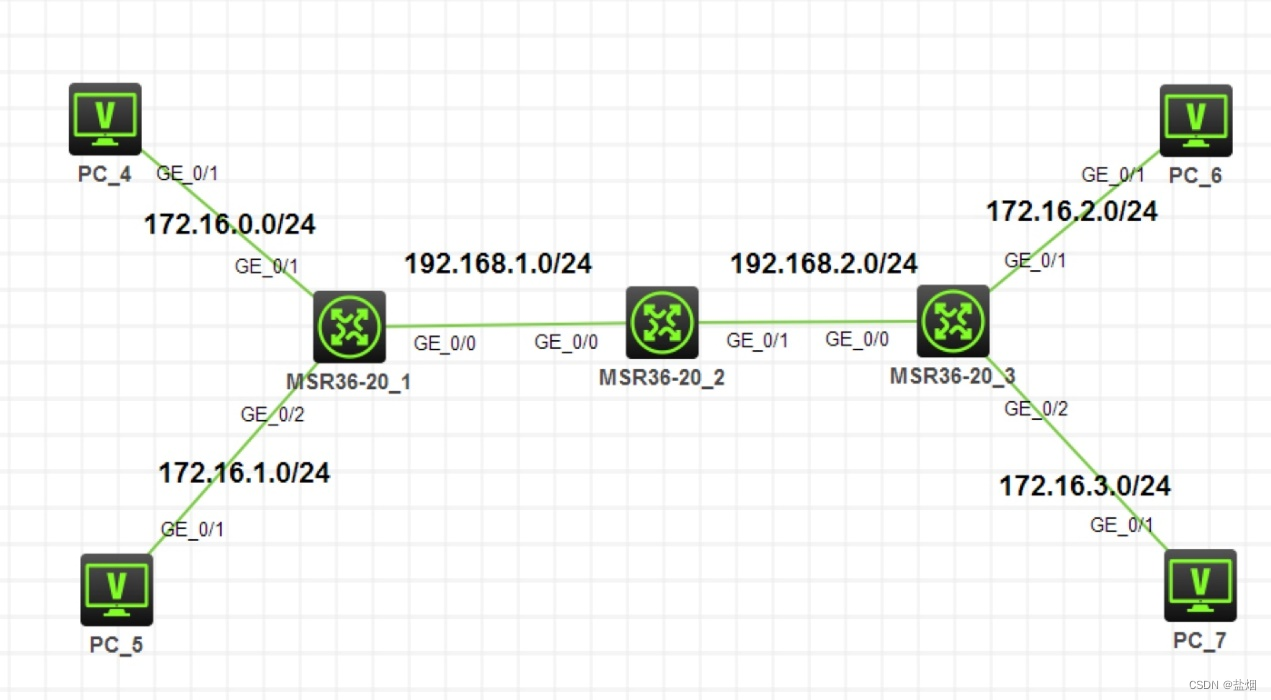
RIP【新华三与华为区别】
【介绍】 rip分为rip 1 与 rip 2 ,rip 2 是对 rip 1 的一种升级,rip 2 可以进行认证等功能 【命令】 新华三: [HC3-R1] rip #启用rip [HC3-R1-rip] version 2 #告知rip 版本号 [HC3-R1-rip] network 192.168.1.0 #宣告其网段 [HC3-R1-rip] …...

Python从入门到精通秘籍四
Python速成,知识点超详细,跟着这个系列边输入边学习体会吧! 一、Python的判断语句的综合案例 下面是一个使用代码示例来详细说明Python判断语句的综合案例,通过用户输入来实现简单的登录验证: # 提示用户输入用户名和密码 username = input("请输入用户名:")…...

rk3568下SoftBusDumpDeviceInfo执行错误—鸿蒙开发已解决
文章目录 项目场景:问题描述原因分析:解决方案:此Bug解决方案总结寄语项目场景: 最近也是遇到了这个问题,看到网上也有人在询问这个问题,本文总结了自己和其他人的解决经验,解决了rk3568下SoftBusDumpDeviceInfo执行错误的问题。 命令行运行 SoftBusDumpDeviceInfo,测…...

Vue 3 Composition API 详解
一、引言 在Vue 3中,引入了一个新的Composition API,旨在提供一种更灵活和可重用的方式来组织组件代码。Composition API基于函数式编程思想,允许开发者将逻辑和状态管理逻辑分离,使代码更加清晰和可维护。 二、Composition API…...
API设计:从基础到最佳实践
1*vWvkkgG6uvgmJT8GkId98A.png 在这次深入探讨中,我们将深入了解API设计,从基础知识开始,逐步进阶到定义出色API的最佳实践。 作为开发者,你可能对许多这些概念很熟悉,但我将提供详细的解释,以加深你的理解…...

每日汇评:由于中东危机削弱了风险偏好,欧元将在1.0900附近波动
随着中东危机的加深,欧元兑美元面临大幅抛售; 由于高通胀,欧洲央行决策者推迟了市场对早期降息的预期; 市场将受到周三公布的美国零售销售数据的影响; 持续的中东紧张局势增强了对避险资产的吸引力,而风险感…...

算法每日一题:删除子串后的字符串最小长度 | 栈 | 字符串
大家好,我是星恒 今天给大家带来的是一道另类的栈的应用 话不多说,我们直接来体验 题目:leetcode 2696 给你一个仅由 大写 英文字符组成的字符串 s 。你可以对此字符串执行一些操作,在每一步操作中,你可以从 s 中删除 …...
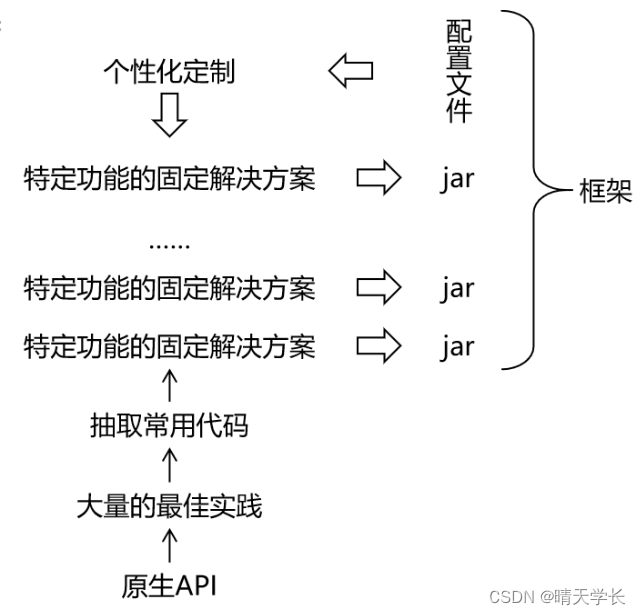
SpringFramework实战指南(一)
SpringFramework实战指南(一) 一、技术体系结构1.1 总体技术体系1.2 框架概念和理解 一、技术体系结构 1.1 总体技术体系 单一架构 一个项目,一个工程,导出为一个war包,在一个Tomcat上运行。也叫all in one。 单一架…...

AtCoder ABC198
本期F为群论题,很有难度。 C - Compass Walking 为了避免精度问题,采用二分推算。但是要小心结果为1的地方。 R 2 ∗ k 2 ≥ x 2 y 2 R^2*k^2\geq x^2y^2 R2∗k2≥x2y2 # -*- coding: utf-8 -*- # time : 2023/6/2 13:30 # file : atcoder.…...

phpinfo和php -m 加载的php.ini不一致
目的: 将phpinfo在web中展示的php.ini和在命令行中展示的php.ini加载路径设置一致。 原本的php.ini加载路劲是: /usr/local/lib/php.ini 解决思路: (1)which php 查看服务器加载的php的位置,这里原来是&a…...

121.买卖股票的最佳时机 122.买卖股票的最佳时机II
121.买卖股票的最佳时机 122.买卖股票的最佳时机II 121.买卖股票的最佳时机 力扣题目链接(opens new window) 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一…...

Spring Boot整理-Spring Boot是什么?
Spring Boot 是一个开源的 Java 基础框架,它旨在简化基于 Spring 的应用开发。其核心特点在于“约定优于配置”的设计哲学,意味着它提供了一系列默认配置,从而帮助开发者更快地启动和运行新的 Spring 应用。Spring Boot 的主要特点包括: 自动配置:Spring Boot 可以根据项目…...

【pytorch】Pytorch 中的 grid 与 各种变换
Pytorch 中的 grid 与 各种变换 数学原理 **单应性(Homography) : 也就是透视变换。**单应性最初用来研究欧几里得几何中的透视和投影,而单应性一词,从词源学上来说,大致意思是“相似的绘图”。单应性的概念被引入来…...
【Linux】线程池实现
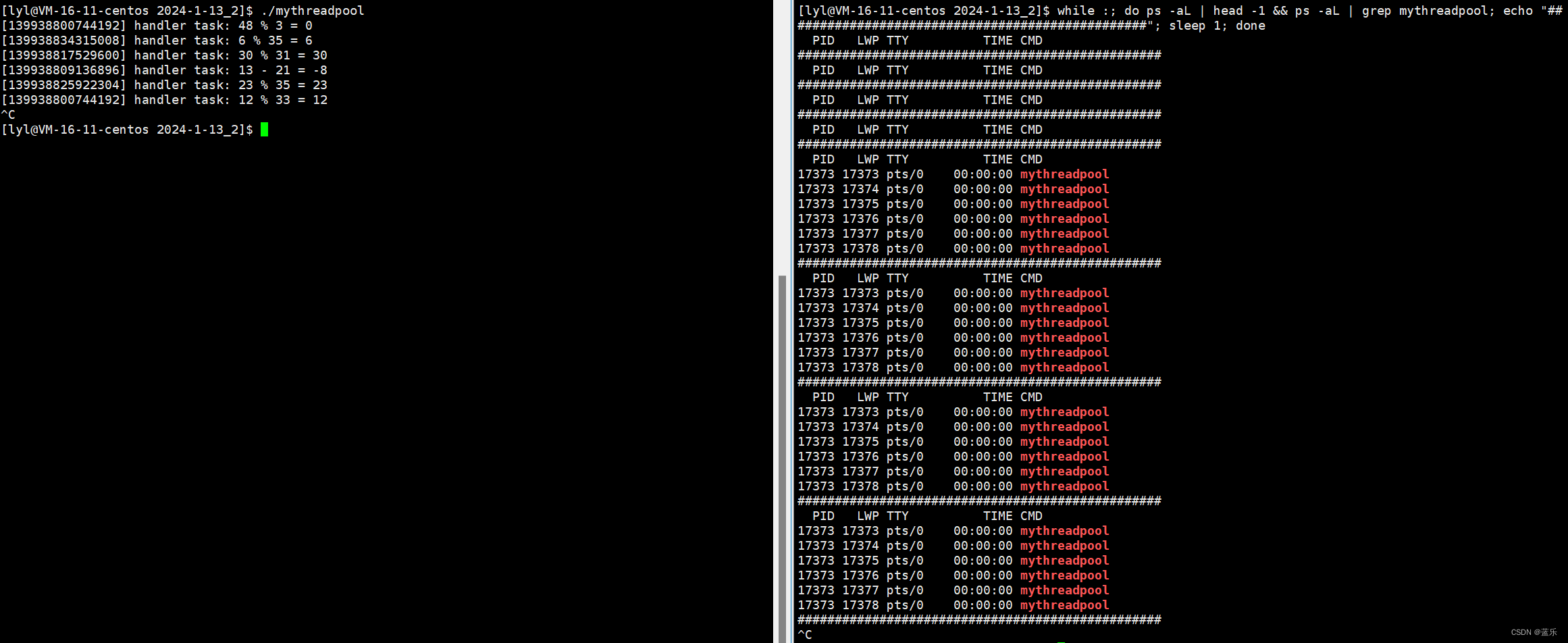
📗线程池实现(单例模式) 1️⃣线程池概念2️⃣线程池代码样例3️⃣部分问题与细节🔸类成员函数参数列表中隐含的this指针🔸单例模式🔸一个失误导致的bug 4️⃣调用线程池完成任务 1️⃣线程池概念 线程池是…...

使用Python批量上传本地maven库到nexus
背景:外包类项目开发时是调用的公司maven仓库进行开发,交付后需要将maven仓库转移到客户环境。 原理:1、打开idea运行源代码,将maven包下载到本地仓库, 2、下载包所在目录中执行脚本将本地仓库的maven包上传到客户nex…...
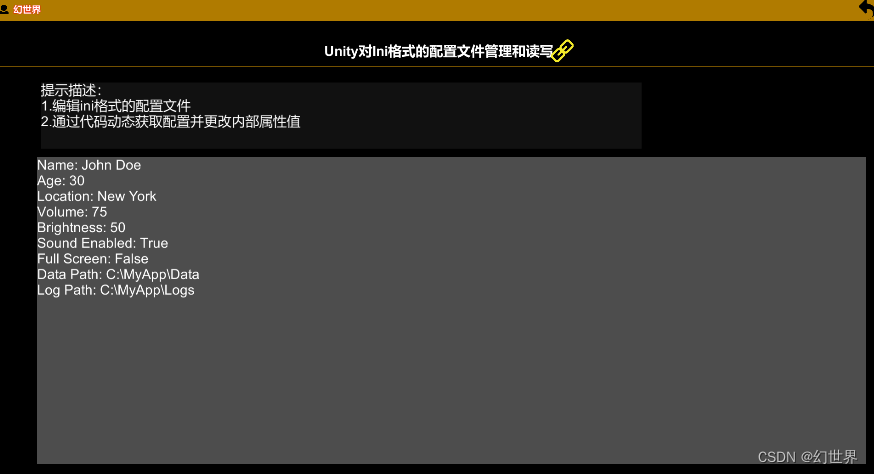
【Unity实战100例】Unity对Ini格式的配置文件管理和读写
目录 一.编写ini格式配置文件 二.读取解析ini文件 三.调用属性 INI 文件以文本形式存储,易于阅读和编辑。这种人可读的格式使得调整配置参数变得更加直观,不需要专门的工具。 INI 文件是一种轻量级的配置文件格式,不需要复杂的解析器或库。它的结构相对简单,适用于小到...

k8s存储卷和数据卷下
静态pv和pvc 运维负责pv:创建号持久化存储卷,申明好读写和挂载类型,以及可以提供的存储空间 Pvc开发做,要和开发沟通好,你期望的读写和挂载类型,以及存储空间 当我发布vc之后可以生成pv,还可以在…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...
