121.买卖股票的最佳时机 122.买卖股票的最佳时机II
121.买卖股票的最佳时机 122.买卖股票的最佳时机II
121.买卖股票的最佳时机
力扣题目链接(opens new window)
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
- 示例 1:
- 输入:[7,1,5,3,6,4]
- 输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。 - 示例 2:
- 输入:prices = [7,6,4,3,1]
- 输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
思路:贪心
这道题目用贪心可以解决,回顾下贪心算法
需要定义局部最优解和整体最优解
题目只要求买卖一次股票,并获取最大利润
要找到股票左侧最低点,并在右侧最高点卖出
找最低点和最高点的流程可以用一个For循环来解决
遍历数组prices,假设遍历的元素就是右侧最高点,在遍历过的元素中找到最低点,即为左侧最低点
计算利润差值即可
局部最优解:找到当前左侧的最低点,计算当前利润最大值
整体最优解:这笔交易中获取的最大利润
时间复杂度o(n)
空间复杂度o(1)
代码如下
public int maxProfit(int[] prices) {if (prices == null || prices.length == 0)return 0;int low = Integer.MAX_VALUE;int maxProfit = 0;for (int i = 0; i < prices.length; i++) {low = Math.min(low, prices[i]);maxProfit = Math.max(maxProfit, prices[i] - low);}return maxProfit;
}
思路:动态规划
思路:动态规划 股票类问题,动态规划解法是通用解法 动态规划五部曲 1.dp数组以及下标代表含义 之前做惯了背包类题目,习惯定义一维数组解决问题。不是背包类题目,要根据题意具体分析 定义一维数组dp[i],表示第i天从这笔交易中获取的最大利润。但买和卖这两种状态无法表示 因此定义二维数组dp[i][j]。j = 0 表示第i天不持有股票利润 j = 1表示第i天持有股票的利润 要用持有和不持有股票作为状态,不用出售和不出售作为状态(因为还要定义【保持卖出状态】和【保持买入状态】) 2.确定递推公式 第i天不持有股票。 1.第i-1天不持有股票 dp[i][0] = dp[i-1][0] 2.第i-1天持有股票 dp[i][0] = prices[i] + dp[i-1][1] dp[i][0] = Math.max(dp[i-1][0],prices[i] + dp[i-1][1]) 第i天持有股票 1.第i-1天不持有股票dp[i][1] = -price[i] 2.第i-1天持有股票dp[i][1] = dp[i-1][1]dp[i][1] = Math.max( -prices[i],dp[i-1][1]) 3.dp数组初始化 dp[0][0] = 0 dp[0][1] = -prices[0] 4.遍历顺序,dp[i]由dp[i-1]推导,故正序 5.举例推导dp数组时间复杂度o(n) 空间复杂度o(n)
代码如下
public static void main(String[] args) {int[] prices = new int[]{7, 1, 5, 3, 6, 4};maxProfit(prices);
}public static int maxProfit(int[] prices) {if (prices == null || prices.length == 0)return 0;int[][] dp = new int[prices.length][2];dp[0][0] = 0;dp[0][1] = -prices[0];for (int i = 1; i < prices.length; i++) {dp[i][0] = Math.max(dp[i - 1][0], prices[i] + dp[i - 1][1]);dp[i][1] = Math.max(-prices[i], dp[i - 1][1]);}return dp[prices.length - 1][0];// 最后一天肯定不持有
}
122.买卖股票的最佳时机II
力扣题目链接(opens new window)
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
- 示例 1:
- 输入: [7,1,5,3,6,4]
- 输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。 - 示例 2:
- 输入: [1,2,3,4,5]
- 输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。 - 示例 3:
- 输入: [7,6,4,3,1]
- 输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
- 1 <= prices.length <= 3 * 10 ^ 4
- 0 <= prices[i] <= 10 ^ 4
思路
思路:动态规划 思路和买卖股票的最佳时机类似,区别在于递推公式 dp[i][0] j = 0表示未持有,此部分逻辑不变 i- 1 持有股票:dp[i][0] = prices[i] + dp[i-1][1] i- 1 未持有股票:dp[i][0] = dp[i-1][0] dp[i][1] j = 1表示持有。i-1未持有股票逻辑变化 i- 1 持有股票:dp[i][1] = dp[i-1][1] i- 1 未持有股票:dp[i][1] = dp[i-1][0] - prices[i] 变化在此处 因为股票可以买卖多次。当前未持有股票的利润,可能包含之前买卖股票的利润 所以需要用之前买卖股票的利润 - 当前持有股票的利润
代码如下
// 时间复杂度o(n)
// 空间复杂度o(n)
public int maxProfitII(int[] prices) {if (prices == null || prices.length == 0)return 0;int[][] dp = new int[prices.length][2];dp[0][0] = 0;dp[0][1] = -prices[0];for (int i = 1; i < prices.length; i++) {dp[i][0] = Math.max(dp[i - 1][0], prices[i] + dp[i - 1][1]);dp[i][1] = Math.max(dp[i - 1][0] - prices[i], dp[i - 1][1]);}return dp[prices.length - 1][0];// 最后一天肯定不持有
}
相关文章:

121.买卖股票的最佳时机 122.买卖股票的最佳时机II
121.买卖股票的最佳时机 122.买卖股票的最佳时机II 121.买卖股票的最佳时机 力扣题目链接(opens new window) 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一…...

Spring Boot整理-Spring Boot是什么?
Spring Boot 是一个开源的 Java 基础框架,它旨在简化基于 Spring 的应用开发。其核心特点在于“约定优于配置”的设计哲学,意味着它提供了一系列默认配置,从而帮助开发者更快地启动和运行新的 Spring 应用。Spring Boot 的主要特点包括: 自动配置:Spring Boot 可以根据项目…...

【pytorch】Pytorch 中的 grid 与 各种变换
Pytorch 中的 grid 与 各种变换 数学原理 **单应性(Homography) : 也就是透视变换。**单应性最初用来研究欧几里得几何中的透视和投影,而单应性一词,从词源学上来说,大致意思是“相似的绘图”。单应性的概念被引入来…...
【Linux】线程池实现
📗线程池实现(单例模式) 1️⃣线程池概念2️⃣线程池代码样例3️⃣部分问题与细节🔸类成员函数参数列表中隐含的this指针🔸单例模式🔸一个失误导致的bug 4️⃣调用线程池完成任务 1️⃣线程池概念 线程池是…...

使用Python批量上传本地maven库到nexus
背景:外包类项目开发时是调用的公司maven仓库进行开发,交付后需要将maven仓库转移到客户环境。 原理:1、打开idea运行源代码,将maven包下载到本地仓库, 2、下载包所在目录中执行脚本将本地仓库的maven包上传到客户nex…...
【Unity实战100例】Unity对Ini格式的配置文件管理和读写
目录 一.编写ini格式配置文件 二.读取解析ini文件 三.调用属性 INI 文件以文本形式存储,易于阅读和编辑。这种人可读的格式使得调整配置参数变得更加直观,不需要专门的工具。 INI 文件是一种轻量级的配置文件格式,不需要复杂的解析器或库。它的结构相对简单,适用于小到...

k8s存储卷和数据卷下
静态pv和pvc 运维负责pv:创建号持久化存储卷,申明好读写和挂载类型,以及可以提供的存储空间 Pvc开发做,要和开发沟通好,你期望的读写和挂载类型,以及存储空间 当我发布vc之后可以生成pv,还可以在…...
SQL Server 配置远程连接
Windows 安装好 SQL Server 的 SSMS,打开SSMS配置远程连接 找到 配置管理器 启用 TCP/IP 打开防火墙设置 新建入站规则 端口TCP - 特定本地端口 (1433)允许连接下一步名称完成 重启 SQL Server 服务...
vscode(visual studio code) 免密登陆服务器
1.生成密钥 首先,在本地,打开命令输入框: WinR–>弹出输入框,输入cmd,打开命令框。 然后,在命令框,输入 ssh-keygen -t rsa -C "love"按两次回车键,问你是否重写,选择…...
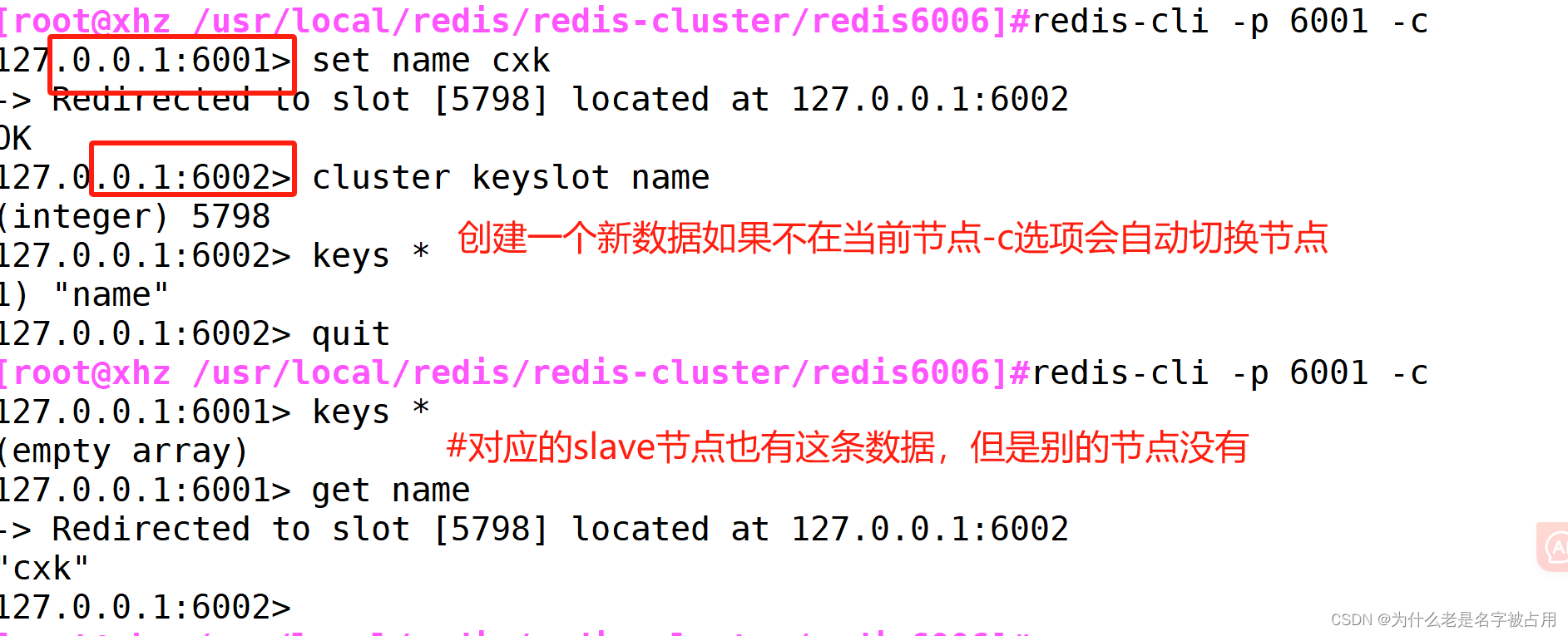
[redis] redis主从复制,哨兵模式和集群
一、redis的高可用 1.1 redis高可用的概念 在web服务器中,高可用是指服务器可以正常访问的时间,衡量的标准是在多长时间内可以提供正常服务(99.9%、99.99%、99.999%等等)。 高可用的计算公式是1-(宕机时间)/(宕机时…...
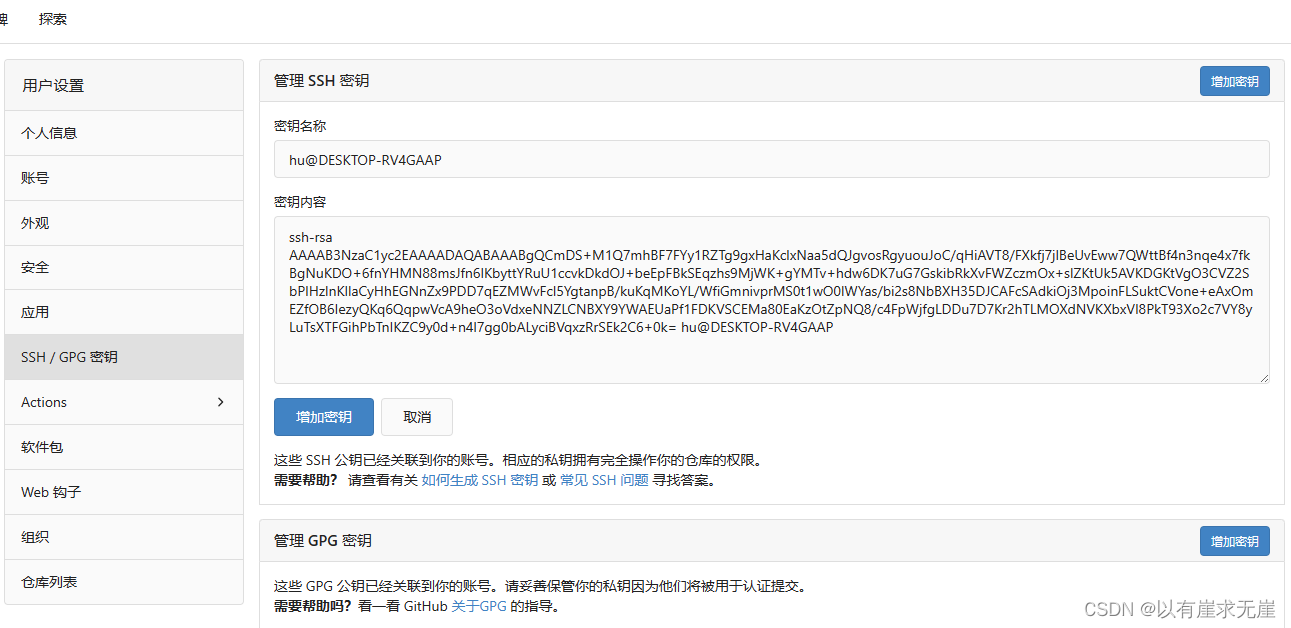
debian12部署Gitea服务
首先安装git、wget、sqlite,然后进行用户和组的相关设置 sudo apt install -y git wget sqlite3 新增一个git用户与一个git组 sudo adduser --system --group --disabled-password --shell /bin/bash --home /home/git --gecos Git Version Control git 给git用户设…...
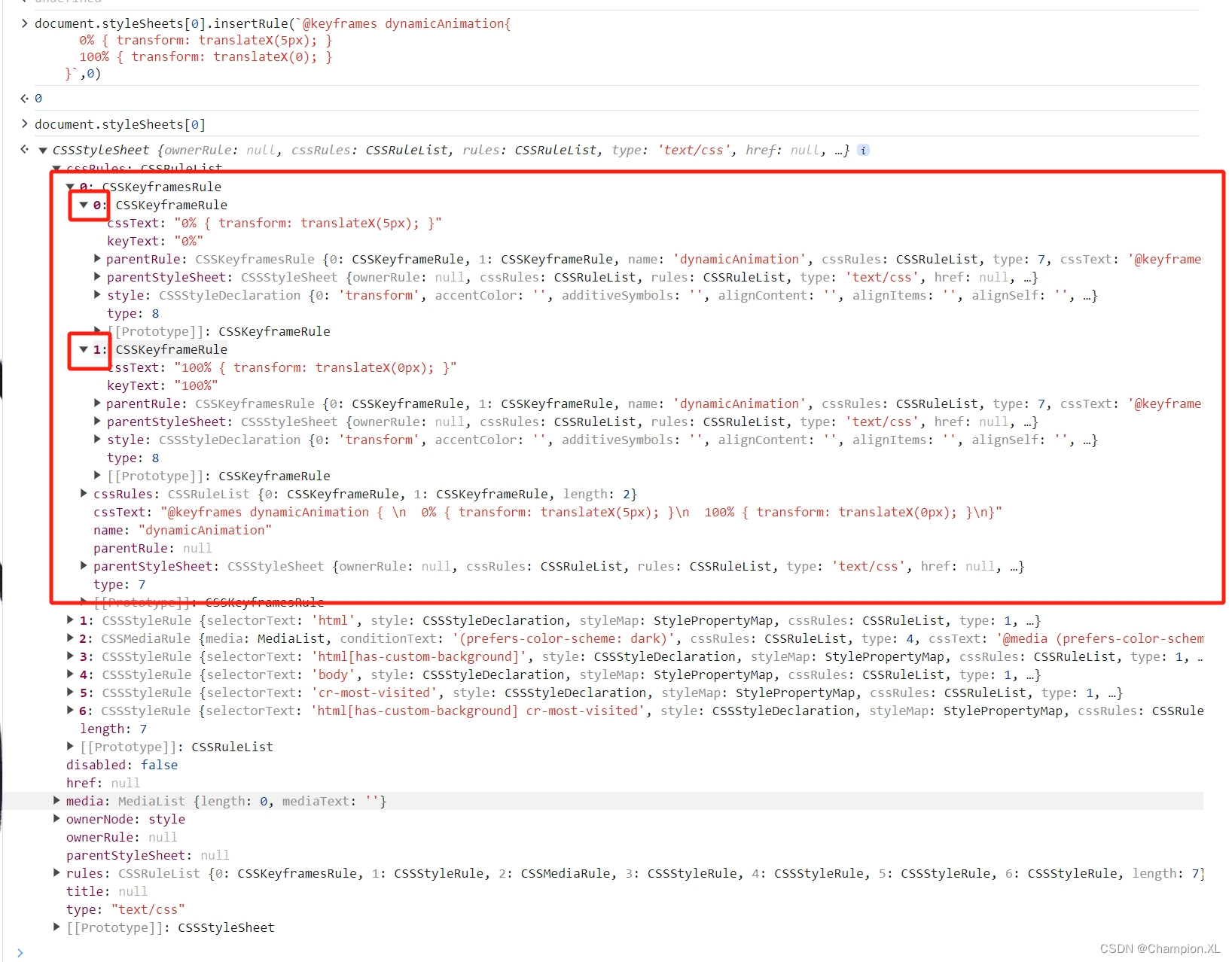
js动态设置关键侦@keyframes
js动态设置关键侦keyframes 1.前置知识 关键侦keyframes规则通过在动画序列中定义关键侦的样式来控制CSS动画序列的中间步骤 keyframes slidein {from {transform: translateX(0%);}to {transform: translateX(100%);} } // from 等价于 0%;to 等价与 100% // 或…...

【WPF.NET开发】流文档
本文内容 什么是流文档?流文档类型创建流内容与流相关的类内容架构自定义文本 流文档旨在优化查看和可读性。 流文档根据运行时变量(例如,窗口大小、设备分辨率和可选的用户首选项)来动态调整和重新排列内容,而不是设…...

golang学习-结构体
1、定义 使用type 和struct 关键字来定义结构体,是值类型 格式如下: type 类型名 struct { 字段名 类型 字段名 类型 ... } 2、实例化 1、var 结构体实例 结构体类型 var p1 Person 2、使用new关键字 var p2 new(Person) 3、使用&对结构体…...
 函数)
Python:enumerate() 函数
enumerate() 函数用于同时遍历索引和元素,常用于循环中。这个函数返回一个包含索引和元素的元组,可以通过解包的方式获取它们。 使用方法: enumerate(iterable, start0). iterable: 要遍历的可迭代对象。start: 索引起始值,默认…...

FPGA 移位运算与乘法
题目: 已知d为一个8位数,请在每个时钟周期分别输出该数乘1/3/7/8,并输出一个信号通知此时刻输入的d有效(d给出的信号的上升沿表示写入有效) 由题意可知: 复位信号高有效,低复位;在inpu_grant上升…...
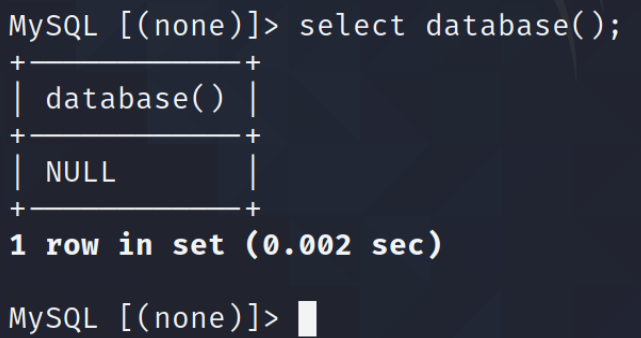
网络安全B模块(笔记详解)- MYSQL信息收集
MYSQL信息收集 1.通过渗透机场景Kali中的渗透测试工具对服务器场景MySQL03进行服务信息扫描渗透测试(使用工具Nmap,使用必须要使用的参数),并将该操作显示结果中数据库版本信息作为Flag提交; Flag:MySQL 5.5.12 2.通过渗透机场景Kali中的渗透测试工具对服务器场景MySQL0…...

从JavaScript的角度上讲解一下xml
- XML(可扩展标记语言) XML(可扩展标记语言)是一种被设计用于存储和传输结构化数据的标记语言。它与HTML相似,但XML并没有预定义的标签,可以自定义标签及其属性。从JavaScript的角度来看,XML可以…...

Pandas实战100例 | 案例 13: 数据分类 - 使用 `cut` 对数值进行分箱
案例 13: 数据分类 - 使用 cut 对数值进行分箱 知识点讲解 在数据分析中,将连续的数值数据分类成不同的区间(或“分箱”)是一种常见的做法。Pandas 提供了 cut 函数,它可以根据你指定的分箱边界将数值数据分配到不同的类别中。 …...
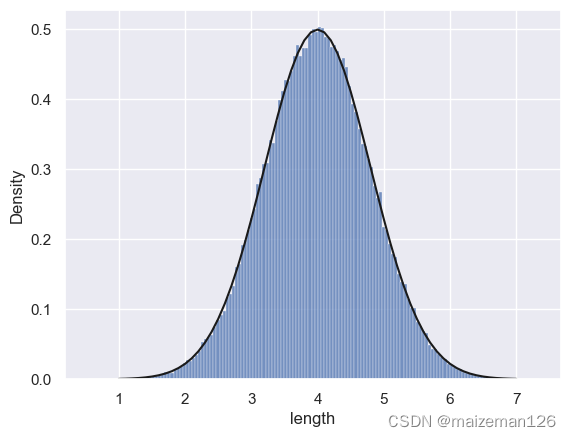
python统计分析——操作案例(模拟抽样)
参考资料:用python动手学统计学 import numpy as np import pandas as pd from matplotlib import pyplot as plt import seaborn as snsdata_setpd.read_csv(r"C:\python统计学\3-4-1-fish_length_100000.csv")[length] #此处将文件路径改为自己的路…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
