python统计分析——操作案例(模拟抽样)
参考资料:用python动手学统计学
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import seaborn as snsdata_set=pd.read_csv(r"C:\python统计学\3-4-1-fish_length_100000.csv")['length'] #此处将文件路径改为自己的路径即可1、抽样
为了保证数据分析的可复现性,使用了随机种子。
np.random.choice()的用法参考:https://blog.csdn.net/maizeman126/article/details/135572042

2、计算样本均值

3、计算总体统计量
相关函数用法参照:python统计分析——单变量描述统计-CSDN博客
mean_t=np.mean(data_set)
std_t=np.std(data_set,ddof=0)
var_t=np.var(data_set,ddof=0)
max_t=np.max(data_set)
min_t=np.min(data_set)print('总体均值:',mean_t)
print('总体标准差:',std_t)
print('总体方差:',var_t)
print('最大值:',max_t)
print('最小值:',min_t)
4、绘制总体的直方图:
直方图的绘制参照:
python统计分析——直方图(plt.hist)_python统计直方图-CSDN博客
python统计分析——直方图(sns.histplot)-CSDN博客
python统计分析——直方图(df.hist)_python df.hist()-CSDN博客
sns.set()
sns.histplot(data_set,kde=False,color='black')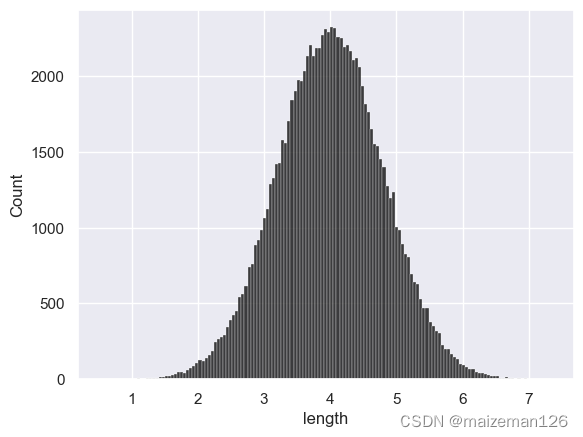
根据总体统计量计算和直方图直观查看,目前可以暂时认为:总体的概率分布服从均值为4,方差为0.64的正态分布,数值的分布范围基本在1-7之间。
5、绘制均值为4,方差为0.64,数据范围为1-7的正态分布的概率密度曲线
5.1 准备1-7上以0.1为公差的等差数列。(注意np.arange函数应用中仍然遵循包左不包右的原则)
x=np.arange(start=1,stop=7.1,step=0.1)
5.2 用stats.norm.pdf计算概率密度。
stats.norm.pdf()函数中,x为分位数,loc表示均值,scale表示标准差(注意不是方差),结果表示取值x时对应的概率密度。
from scipy import stats
pro_d=stats.norm.pdf(x=x,loc=4,scale=0.8)
pro_d
5.3 绘制概率密度曲线
plt.plot(x,pro_d,color='k') #k表示颜色black的简写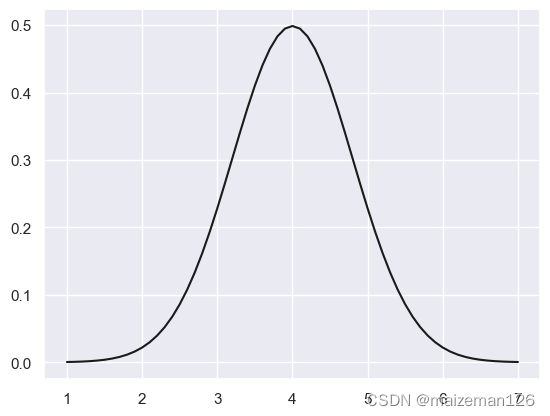
5.4 将总体直方图和正态分布概率密度函数放到一个中显示:
sns.histplot(data_set,stat='density',kde=False)
plt.plot(x,pro_d,color='k')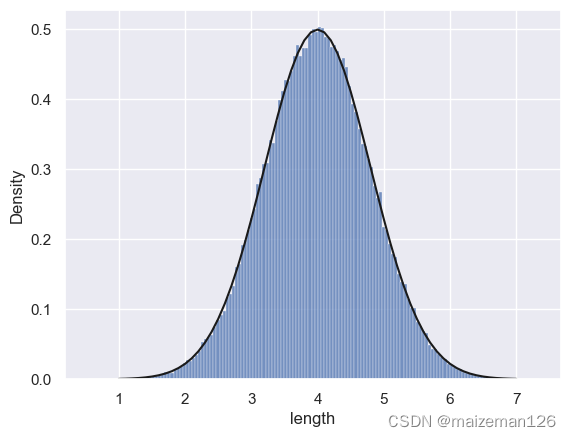
根据上图可以看出:正态分布的概率密度和总体分布的概率密度几乎吻合,因此可以认为总体服从正态分布。
相关文章:

python统计分析——操作案例(模拟抽样)
参考资料:用python动手学统计学 import numpy as np import pandas as pd from matplotlib import pyplot as plt import seaborn as snsdata_setpd.read_csv(r"C:\python统计学\3-4-1-fish_length_100000.csv")[length] #此处将文件路径改为自己的路…...

部署Tomcat及其负载均衡
Tomcat服务器是一个免费的开放源代码的Web应用服务器,属于轻量级应用服务器,在中小型系统和并发访问用户不是很多的场合下被普遍使用,是开发和调试JSP程序的首选。一般来说,Tomcat虽然和Apache或者Nginx这些Web服务器一样…...

C++ 类、结构体
C 类、结构体 类可以将变量、数组和函数完美地打包在一起。 类与结构体 类的定义: class Person {private:int age,height;double money;string books[100];public:string name;void say(){cout<<"Im"<<name<<endl;}int get_age(){…...
数据结构(三)堆和哈希表
目录 哈希表和堆什么是哈希表 ?什么是堆 ?什么是图 ?案例一:使用python实现最小堆案例二 : 如何用Python通过哈希表的方式完成商品库存管理闯关题 (包含案例三:python实现哈希表) 本…...

李宏毅LLM——ChatGPT原理剖析
文章目录 Chat-GPT引言关键技术——预训练研究问题玩文字冒险游戏 ChatGPT原理剖析 Chat-GPT引言 直观感受:结果有模有样、每次输出结果都不同、可以追问、幻想出的答案误解:罐头回答、答案是网络搜索的结果真正做的事:文字接龙,…...

让Windows上vscode的C语言scanf函数可以读取中文字符
windows的默认字符集保存为GBK不要修改 区域设置–时钟和区域–区域–管理–更系统区域设置–(不要勾选)使用UTF-8。 查看验证当前字符集: cmdchcp 活动代码页: 936936就是简体中文GBK vscode的setting.json文件添加如下代码 点击左下角…...

Linux命令(3)
一. tr 对字符进行处理: tr 命令用于字符转换、替换和删除,主要用于删除文件中的控制符或进行字符串转换等。 将a转换成1 将小写字母转换成大写 压缩: tr -s 将a压缩成一个a 将空格压缩成一个 删除: tr -d 补集: 用字符串中的字符集的补…...
音频采集编码写入详细源码分析)
安卓MediaRecorder(3)音频采集编码写入详细源码分析
文章目录 前言音频采集音频初始化AudioRecord 分析AudioSource 采集到音频 音频编码音频编码后数据处理MPEG4Writer写入音频编码后数据到文件MPEG4Writer::Track 取编码后的音频编数据结语 本文首发地址 https://blog.csdn.net/CSqingchen/article/details/134896808 最新更新地…...
)
2024年网络安全竞赛—网络安全事件分析应急响应解析(包含FLAG)
网络安全事件分析应急响应 目录 网络安全事件分析应急响应 解析如下:...
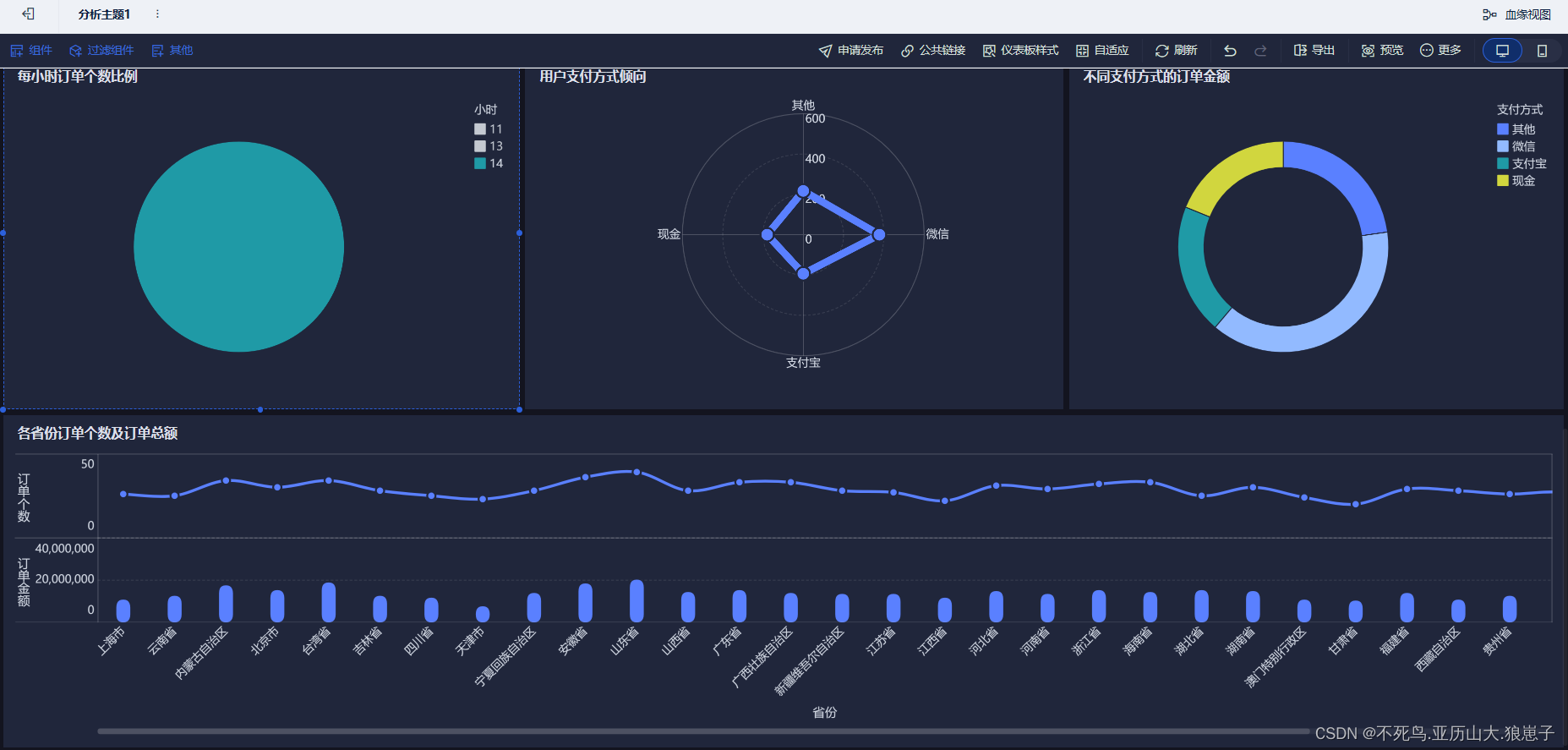
FineBI实战项目一(22):各省份订单个数及订单总额分析开发
点击新建组件,创建各省份订单个数及订单总额组件。 选择自定义图表,将province拖拽到横轴,将cnt和total拖拽到纵轴。 调节纵轴的为指标并列。 修改横轴和纵轴的标题。 修改柱状图样式: 将组件拖拽到仪表板。 结果如下:…...

2024.1.16 调用tinyspline样条曲线拟合库时报 stack smashing detected,CMakeLists.txt中屏蔽该异常
在函数中调用第三方库api拟合样条曲线,函数中一切正常,可以打印所有数组变量,重复执行该函数,某一次函数return时报 stack smashing deteced (unknown) ,原因可能是第三方库内部的函数有栈溢出风…...

Leetcode202快乐数(java实现)
今天分享的题目是快乐数: 快乐数的定义如下: 快乐数(Happy Number)是指一个正整数,将其替换为各个位上数字的平方和,重复这个过程直到最后得到的结果为1,或者无限循环但不包含1。如果最终结果为…...
)
50天精通Golang(第13天)
反射reflect 一、引入 先看官方Doc中Rob Pike给出的关于反射的定义: Reflection in computing is the ability of a program to examine its own structure, particularly through types; it’s a form of metaprogramming. It’s also a great source of confus…...
大数据 - Doris系列《三》- 数据表设计之表的基本概念
目录 🐶3.1 字段类型 🐶3.2 表的基本概念 3.2.1 Row & Column 3.2.2 分区与分桶 🥙3.2.2.1 Partition 1. Range 分区 2. List 分区 进阶:复合分区与单分区的选择 3.2.3 PROPERTIES 🥙3.2.3.1 分片副本数 …...

数据库mysql no.3
1.排序查询 order by 排序列表 【asc/desc】 排序列表:可以是单个字段、多个字段、表达式、函数、别名。 asc 升序 desc 降序 如果没有写那就是默认升序 2.常见函数 select 函数名(); 定义:函…...
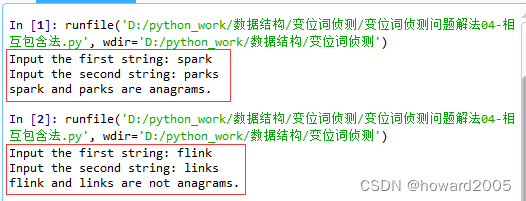
数据结构实战:变位词侦测
文章目录 一、实战概述二、实战步骤(一)逐个比较法1、编写源程序2、代码解释说明(1)函数逻辑解释(2)主程序部分 3、运行程序,查看结果4、计算时间复杂度 (二)排序比较法1…...
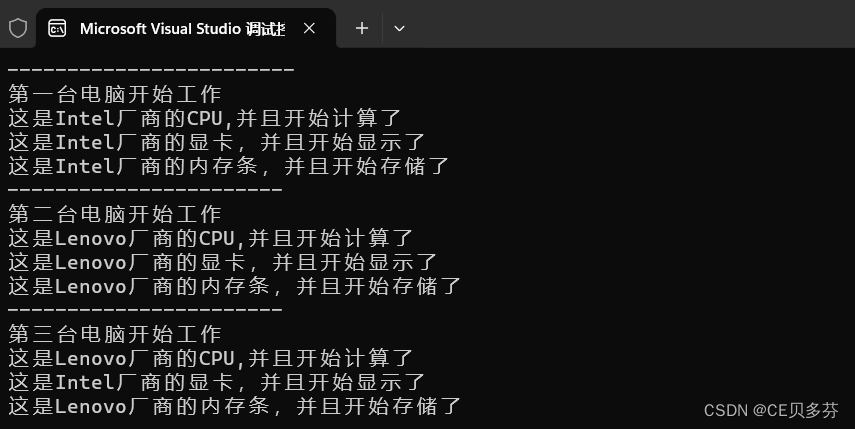
C++核心编程之类和对象---C++面向对象的三大特性--多态
目录 一、多态 1. 多态的概念 2.多态的分类: 1. 静态多态: 2. 动态多态: 3.静态多态和动态多态的区别: 4.动态多态需要满足的条件: 4.1重写的概念: 4.2动态多态的调用: 二、多态 三、多…...
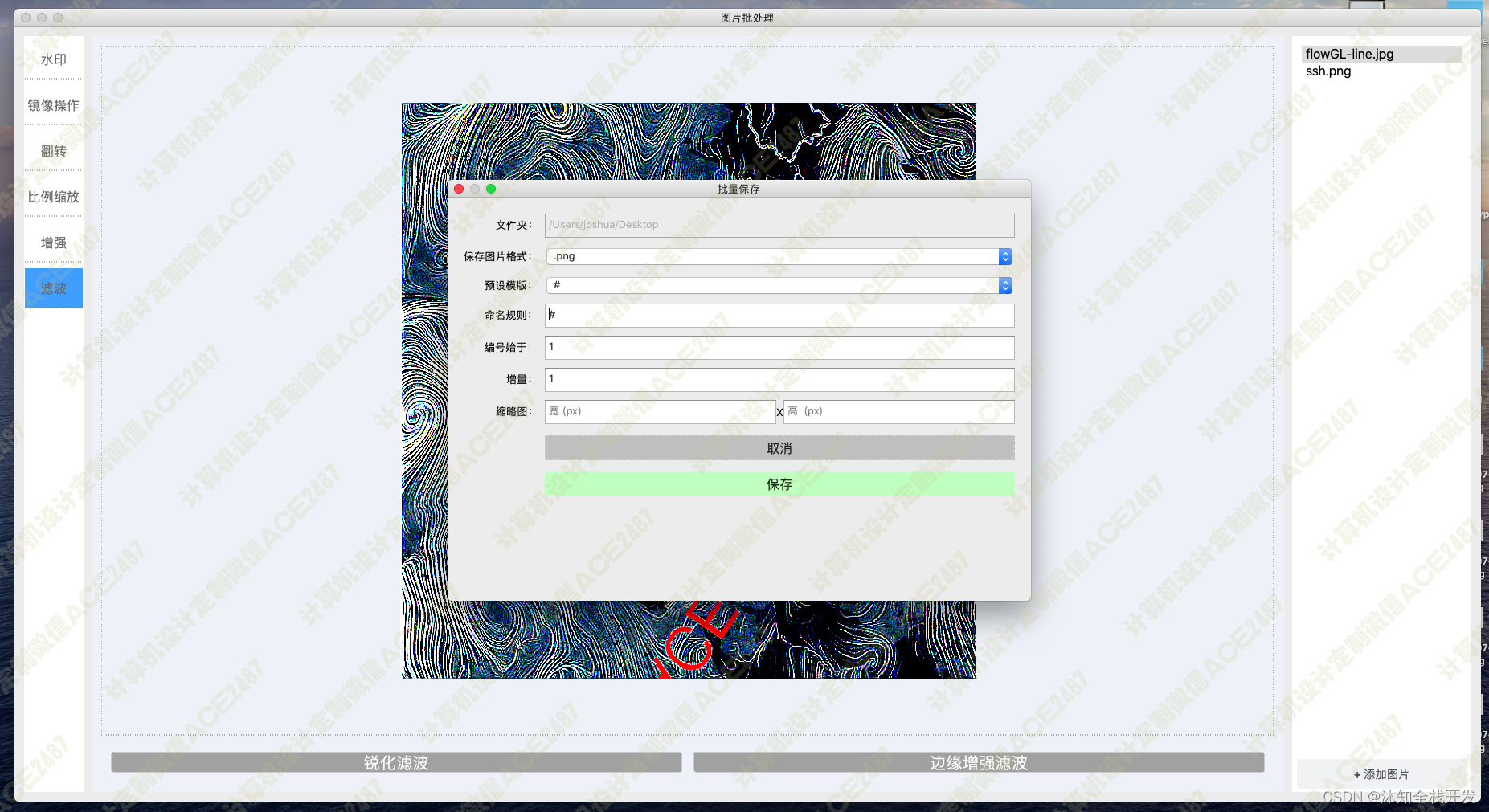
基于PyQT的图片批处理系统
项目背景: 随着数字摄影技术的普及,人们拍摄和处理大量图片的需求也越来越高。为了提高效率,开发一个基于 PyQt 的图片批处理系统是很有意义的。该系统可以提供一系列图像增强、滤波、水印、翻转、放大缩小、旋转等功能,使用户能够…...

vscode文件配置
lanuch.json {"version": "0.2.0","configurations": [{"name": "(gdb) 启动","type": "cppdbg","request": "launch",// "program": "输入程序名称,例…...

C++学习笔记——SLT六大组件及头文件
目录 一、C中STL(Standard Template Library) 二、 Gun源代码开发精神 三、 实现版本 四、GNU C库的头文件分布 bits目录 ext目录 backward目录 iostream目录 stdexcept目录 string目录 上一篇文章: C标准模板库(STL&am…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...
