微服务治理:微服务安全详解
微服务安全旨在保护微服务架构中每一个独立的服务。与传统单体应用程序不同,它们在单点应用安全措施,微服务由于其独立性,需要分布式安全方法。
为何关注微服务安全?
- 攻击面扩大: 更多服务暴露在外,意味着攻击者拥有更多潜在的入口。
- 数据碎片化: 数据分散在各个服务中,增加了安全和隐私维护难度。
- 通信复杂性: 服务间的通信面临独特安全挑战,需要安全通道和授权机制。
微服务安全关键方面:
1. API 安全: 安全的 API 是微服务的入口,包括:
- 身份验证和授权: 验证用户和服务身份,并强制执行访问控制规则。
- 输入验证: 清理用户输入以防止注入攻击。
- 数据加密: 加密静止和传输中的数据以保护敏感信息。
2. 服务间安全: 服务间安全通信至关重要,包括:
- 安全通信协议: 使用 HTTPS 和其他安全协议进行加密通信。
- 相互认证: 验证参与通信的每个服务的身份。
- 服务调用授权: 只有授权的服务才能相互交互。
3. 基础设施安全: 保护承载微服务的基础设施,包括:
- 容器和虚拟机安全: 保护运行服务的容器或虚拟机。
- 网络安全: 部署防火墙和其他网络安全措施。
- 日志记录和监控: 监控日志和指标,发现可疑活动。
微服务安全最佳实践:
- 安全设计: 从一开始就将安全融入微服务,而非事后添加。
- 使用标准协议和库: 利用成熟的安全协议和库,避免漏洞。
- 最小化暴露面: 只将必要的 API 和功能暴露给外部世界。
- 最小权限原则: 仅授予服务其运行所需的最低权限。
- 自动化安全流程: 自动化安全任务,例如漏洞扫描和修补。
- 持续监控和测试: 定期监控系统安全威胁,并进行渗透测试以识别漏洞。
通过实施这些最佳实践并关注微服务安全的关键方面,您可以构建安全、弹性的微服务,保护您的数据、用户和应用程序。
相关文章:

微服务治理:微服务安全详解
微服务安全旨在保护微服务架构中每一个独立的服务。与传统单体应用程序不同,它们在单点应用安全措施,微服务由于其独立性,需要分布式安全方法。 为何关注微服务安全? 攻击面扩大: 更多服务暴露在外,意味着攻击者拥有…...
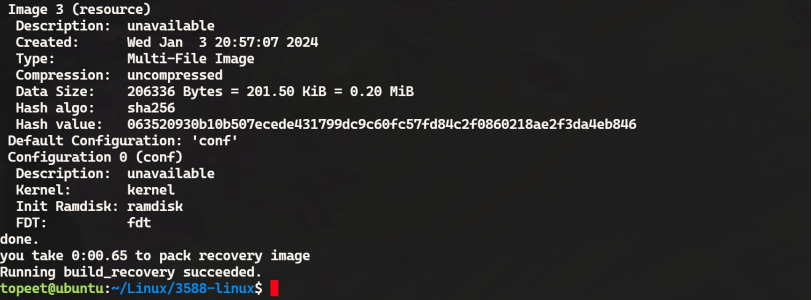
迅为RK3588开发板编译 Buildroot单独编译图形化界面三
第三步:编译 Recovery 首先在 linux 源码目录下输入以下命令进入编译的 UI 界面,进入之后如下所示: ./build.sh 然后将光标移动到第四个 recovery,点击回车即可开始 recovery 的编译,编译过程如下所示: 编…...

yum仓库及NFS共享
目录 一.yum仓库的基本原理 1.Yum概述: 2.Yum实现过程: 二. yum配置文件及命令: 1. 主配置文件: 2. 仓库设置文件: 3 .日志文件: 编辑4.yum命令详解: 三. 搭建仓库的方式: …...
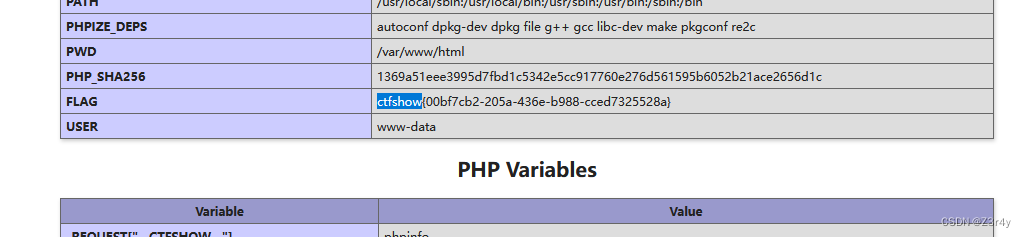
【Web】CTFSHOW PHP特性刷题记录(全)
知其然知其所以然,尽量把每种特性都详细讲明白。 目录 web89 web90 web91 web92 web93 web94 web95 web96 web97 web98 web99 web100 web101 web102 web103 web104 web105 web106 web107 web108 web109 web110 web111 web112 web113 web…...
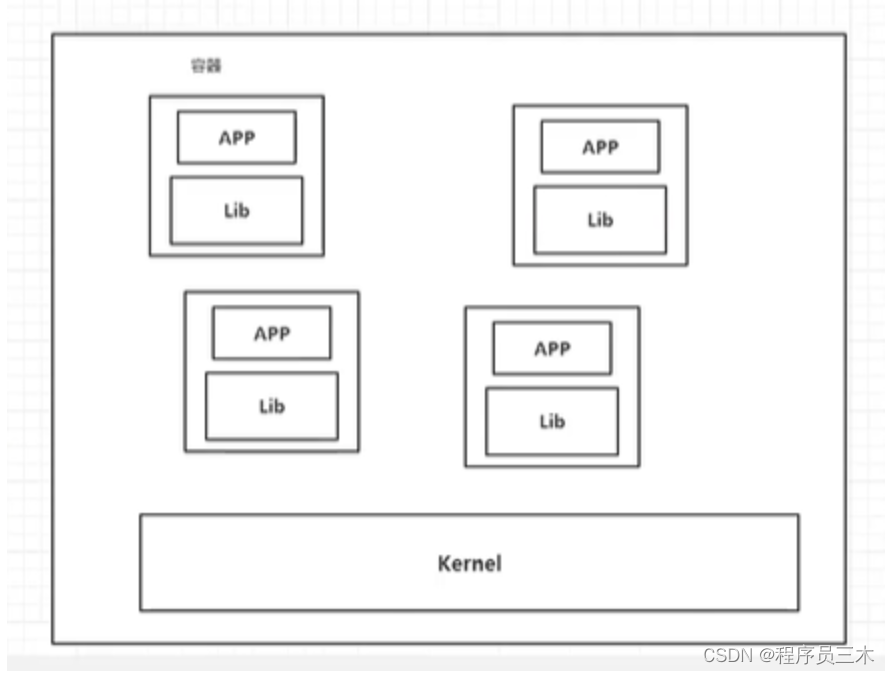
[Docker] Docker为什么出现
Docker为什么出现 一款产品: 开发–上线 -->两套环境 | 应用配置 开发即运维! 环境配置十分麻烦,每一个机器都要部署环境(Redis, ES, Hadoop) 费时费力 项目带上配置环境安装打包。 传统: 开发jar&…...

小程序基础学习(页面跳转传参)
目录 正向传参 原理:直接在url里面拼接参数即可 接受参数 编辑 已经跳转到的页面用onLoad函数来接受即可然后写回页面展示即可 逆向传参 原理:通过使用 getCurrentPages()这个方法来获取返回页面列表,然后再用页面.setDataÿ…...
)
面试经典150题(85-87)
leetcode 150道题 计划花两个月时候刷完,今天(第四十三天)完成了3道(85-87)150: 85.(77. 组合)题目描述: 给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。 你可…...

【C++】“Hello World!“
🦄个人主页:修修修也 🎏所属专栏:C ⚙️操作环境:Visual Studio 2022 2024.1.14 纪念一下自己编写的第一个C程序 #include<iostream>int main() {/*我的第一个C程序*/std::cout << "Hello world!:>" <<std::endl;ret…...

系统性学习vue-vue中的ajax
vue中的ajax 配置代理常用发送Ajax请求方式跨域方式一方式二 vue-resource插槽默认插槽具名插槽作用域插槽 配置代理 常用发送Ajax请求方式 xhr new XMLHttpRequest() 在真正开发中不常用,比较麻烦jQuery 封装了xhraxios 封装了xhr 与jQuery相比优势是:…...

【PGSQL】date_trunc 函数
date_trunc 函数用于在 PostgreSQL 中将日期或时间戳值截断(向下取整)到指定的精度级别。当您想要忽略较小的时间单位(例如,小时、分钟、秒),专注于较大的单位(例如,天、月、年&…...

使用composer生成的DMG和PKG格式软件包有何区别
在使用Composer从包源构建软件包时候,有两种不同类型的包:PKG和DMG。你知道两者之间的区别吗? 以及如何选取吗? 每种格式都有各自的优势具体取决于软件包的预期用途以及用于部署软件包的工具。下面我们来了解一下PKG和DMG格式的区别和用途。…...

Linux 压缩解压
.tar (注:tar是打包,不是压缩!) 解包:tar xvf FileName.tar -C DirName打包:tar cvf FileName.tar DirName .gz 解压1:gunzip FileName.gz解压2:gzip -d FileName.gz压…...

YUM仓库和NFS共享
目录 一、yum仓库 1. yum仓库介绍 1.1 简介 1.2 实现过程 1.3 实现安装服务 2. yum配置文件及命令 2.1 yum配置文件 2.1.1 yum主配置文件 2.1.2 仓库设置文件 2.1.3 日志文件 2.2 yum命令详解 2.2.1 查询 2.2.2 yum安装升级 2.2.3 软件卸载 3. 搭建仓库的方式 …...

Springboot中时间格式化
时间格式化方式 JsonFromat方式全局配置方式格式化工具方式 JsonFromat方式 前端传参或后端响应 yyyy-MM-dd HH:mm:ss 格式,直接属性字段上加注解 JsonFromat JsonFromat(pattern "yyyy-MM-dd HH:mm:ss", timezone "GMT8") private Date fi…...
蓝桥杯基础知识3 memset()
蓝桥杯基础知识3 memset() #include <bits/stdc.h> using namespace std;int main(){int a[5]; //随机数for(int i 0;i < 5; i)cout << a[i] << \n;cout << \n;memset(a, 0, sizeof a); //0for(int i 0;i < 5; i)cout << a[i] << …...
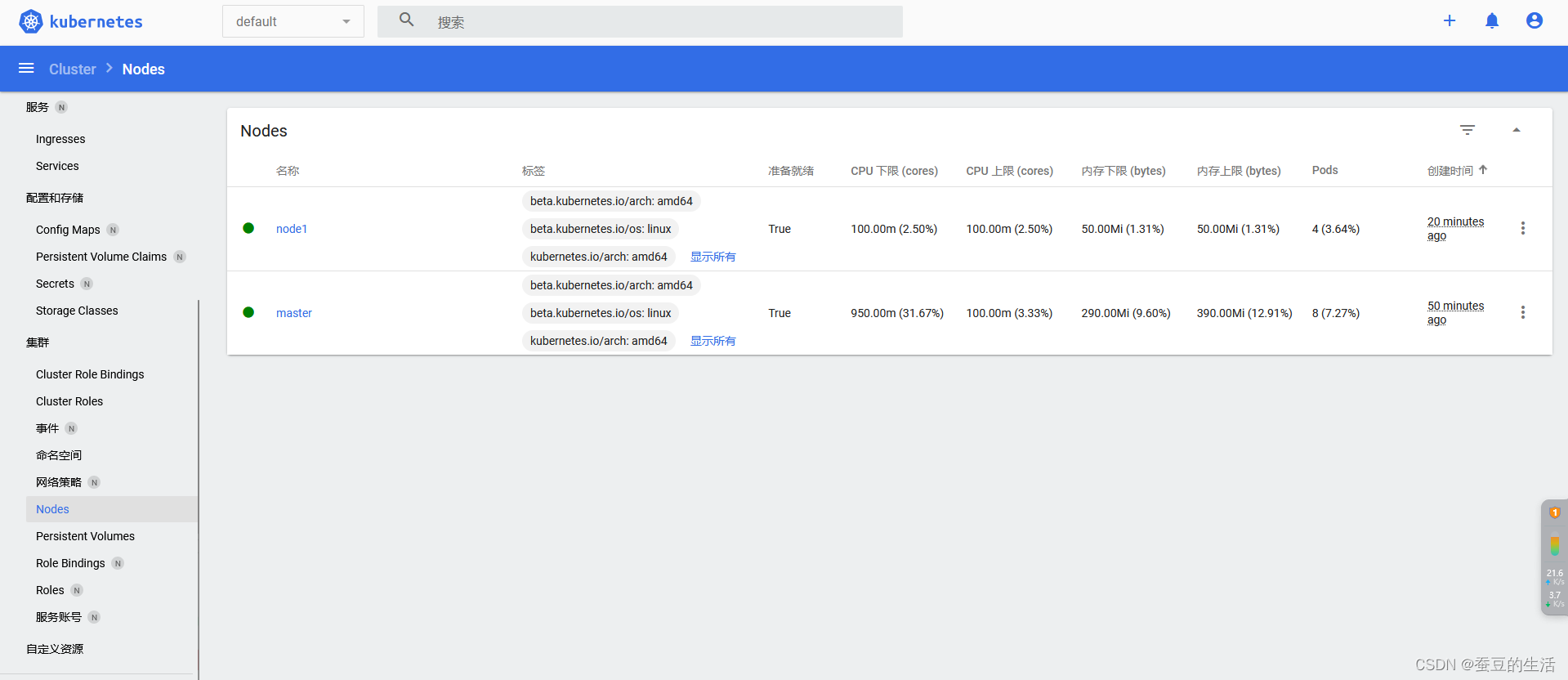
CentOS安装k8s单机/集群及一些命令
目录 前言 1. 安装docker 2. 安装要求 3.准备网络(如果只装单机版可跳过此部) 4. 准备工作 5. 安装 5.1. 配置阿里云yum k8s源 5.2 安装kubeadm、kubectl和kubelet 5.3 初始化,只在master执行,子节点不要执行 5.3.1 一些…...

iOS和安卓端个人踩坑史
本公司不提供测试机,借手机是开发测试中最麻烦的事 iOS可行组 1、iOS可以播放视频无声音,Andorid有声音 当时做了个远程视频连接项目,使用了jitsi第三方视频服务,iOS没有加dom.play()导致无法接收声音 2、iOS可以长按保存图片…...
)
前端面试Vue部分补充(详细)
1、vue的基本原理 Vue的基本原理是基于MVVM(Model-View-ViewModel)模式的前端框架。它通过数据绑定和响应式系统来实现数据和视图的自动同步更新。 Vue的基本原理可以概括为以下几个步骤: 1). 解析模板:Vue通过解析模板来生成虚…...

计算机网络重点简答题
文章目录(持续更新) 计算机网络重点简答题📣一、什么是TCP/IP的五层参考模型?✨1.是什么✨2.主要功能✨3.数据包的封装和解封装 📣二、TCP与UDP的区别? 计算机网络重点简答题 📣一、什么是TCP/…...
自定义字典及分词器)
【迅搜17】SCWS分词(二)自定义字典及分词器
SCWS分词(二)自定义字典及分词器 经过上篇文章的学习,相信大家对分词的概念已经有了更深入的了解了吧。我们也知道了,SCWS 是 XS 中的一个重要组成部分,但它也是可以单独拿出来使用的。而对于分词器来说,不…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...
