Linux 压缩解压
.tar
(注:tar是打包,不是压缩!)
- 解包:tar xvf FileName.tar -C DirName
- 打包:tar cvf FileName.tar DirName
.gz
- 解压1:gunzip FileName.gz
- 解压2:gzip -d FileName.gz
- 压缩:gzip FileName
.tar.gz
- 解压:tar zxvf FileName.tar.gz -C DirName
- 压缩:tar zcvf FileName.tar.gz DirName
.bz2
- 解压1:bzip2 -d FileName.bz2
- 解压2:bunzip2 FileName.bz2
- 压缩: bzip2 -z FileName
.tar.bz2
- 解压:tar jxvf FileName.tar.bz2
- 压缩:tar jcvf FileName.tar.bz2 DirName
.tar.Z
- 解压:tar Zxvf FileName.tar.Z
- 压缩:tar Zcvf FileName.tar.Z DirName
.tgz
- 解压:tar zxvf FileName.tgz
- 压缩:tar zcvf FileName.tgz FileName
.tar.tgz
- 解压:tar zxvf FileName.tar.tgz
- 压缩:tar zcvf FileName.tar.tgz FileName
.zip
- 解压:unzip FileName.zip
- 压缩:zip FileName.zip DirName
-
zip -j demo.zip /root/delete.sh /home/stop.py # j: 只压缩文件 不创建层级目录
.rar
- 解压:rar a FileName.rar
- 压缩:rar e FileName.rar
压缩参数
- --no-same-owner:目录权限会使用当前操作用户的权限作为文件的所属
相关文章:

Linux 压缩解压
.tar (注:tar是打包,不是压缩!) 解包:tar xvf FileName.tar -C DirName打包:tar cvf FileName.tar DirName .gz 解压1:gunzip FileName.gz解压2:gzip -d FileName.gz压…...

YUM仓库和NFS共享
目录 一、yum仓库 1. yum仓库介绍 1.1 简介 1.2 实现过程 1.3 实现安装服务 2. yum配置文件及命令 2.1 yum配置文件 2.1.1 yum主配置文件 2.1.2 仓库设置文件 2.1.3 日志文件 2.2 yum命令详解 2.2.1 查询 2.2.2 yum安装升级 2.2.3 软件卸载 3. 搭建仓库的方式 …...

Springboot中时间格式化
时间格式化方式 JsonFromat方式全局配置方式格式化工具方式 JsonFromat方式 前端传参或后端响应 yyyy-MM-dd HH:mm:ss 格式,直接属性字段上加注解 JsonFromat JsonFromat(pattern "yyyy-MM-dd HH:mm:ss", timezone "GMT8") private Date fi…...
蓝桥杯基础知识3 memset()
蓝桥杯基础知识3 memset() #include <bits/stdc.h> using namespace std;int main(){int a[5]; //随机数for(int i 0;i < 5; i)cout << a[i] << \n;cout << \n;memset(a, 0, sizeof a); //0for(int i 0;i < 5; i)cout << a[i] << …...
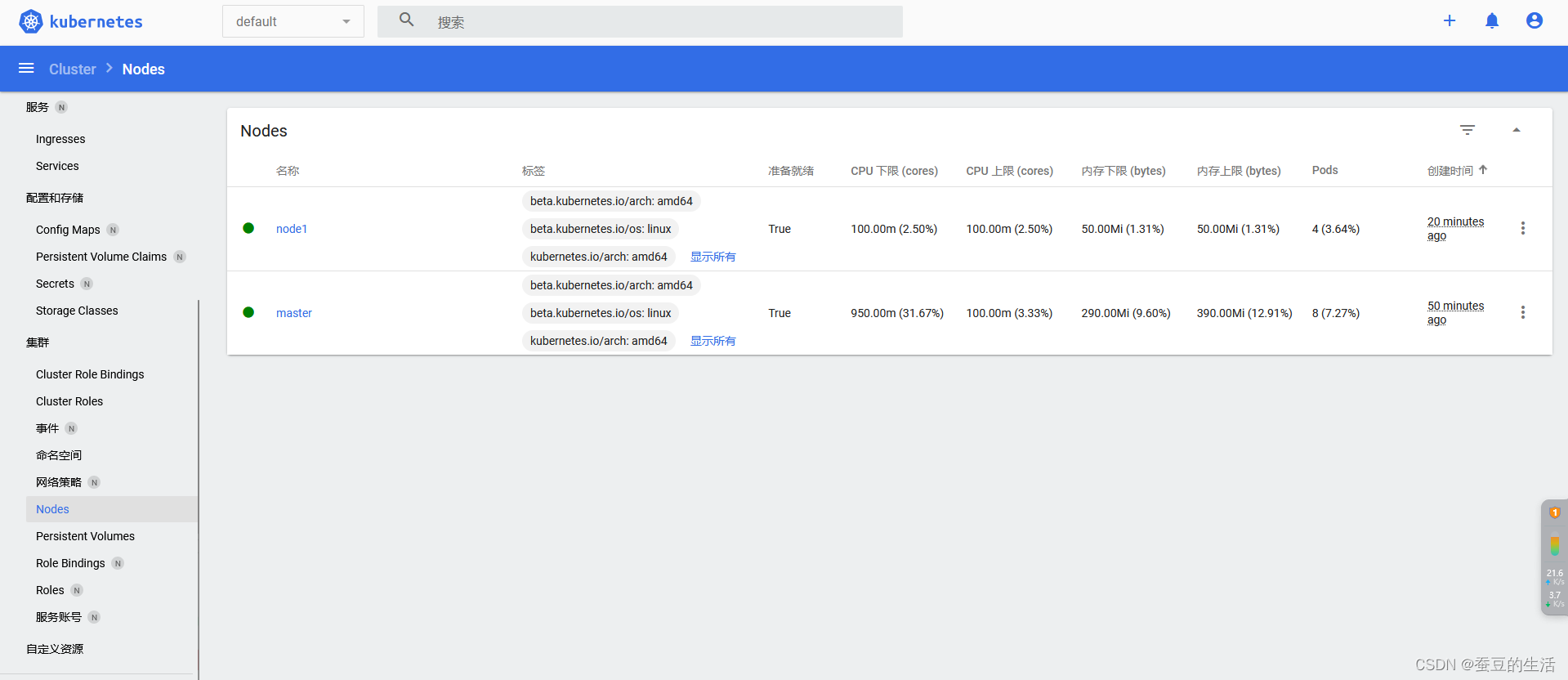
CentOS安装k8s单机/集群及一些命令
目录 前言 1. 安装docker 2. 安装要求 3.准备网络(如果只装单机版可跳过此部) 4. 准备工作 5. 安装 5.1. 配置阿里云yum k8s源 5.2 安装kubeadm、kubectl和kubelet 5.3 初始化,只在master执行,子节点不要执行 5.3.1 一些…...

iOS和安卓端个人踩坑史
本公司不提供测试机,借手机是开发测试中最麻烦的事 iOS可行组 1、iOS可以播放视频无声音,Andorid有声音 当时做了个远程视频连接项目,使用了jitsi第三方视频服务,iOS没有加dom.play()导致无法接收声音 2、iOS可以长按保存图片…...
)
前端面试Vue部分补充(详细)
1、vue的基本原理 Vue的基本原理是基于MVVM(Model-View-ViewModel)模式的前端框架。它通过数据绑定和响应式系统来实现数据和视图的自动同步更新。 Vue的基本原理可以概括为以下几个步骤: 1). 解析模板:Vue通过解析模板来生成虚…...

计算机网络重点简答题
文章目录(持续更新) 计算机网络重点简答题📣一、什么是TCP/IP的五层参考模型?✨1.是什么✨2.主要功能✨3.数据包的封装和解封装 📣二、TCP与UDP的区别? 计算机网络重点简答题 📣一、什么是TCP/…...
自定义字典及分词器)
【迅搜17】SCWS分词(二)自定义字典及分词器
SCWS分词(二)自定义字典及分词器 经过上篇文章的学习,相信大家对分词的概念已经有了更深入的了解了吧。我们也知道了,SCWS 是 XS 中的一个重要组成部分,但它也是可以单独拿出来使用的。而对于分词器来说,不…...

深度学习记录--偏差/方差(bias/variance)
误差问题 拟合神经网络函数过程中会出现两种误差:偏差(bias)和方差(variance) 偏差和误差的区别 欠拟合(underfitting) 当偏差(bias)过大时,如左图,拟合图像存在部分不符合值,称为欠拟合(underfitting) 过拟合(overfitting) …...
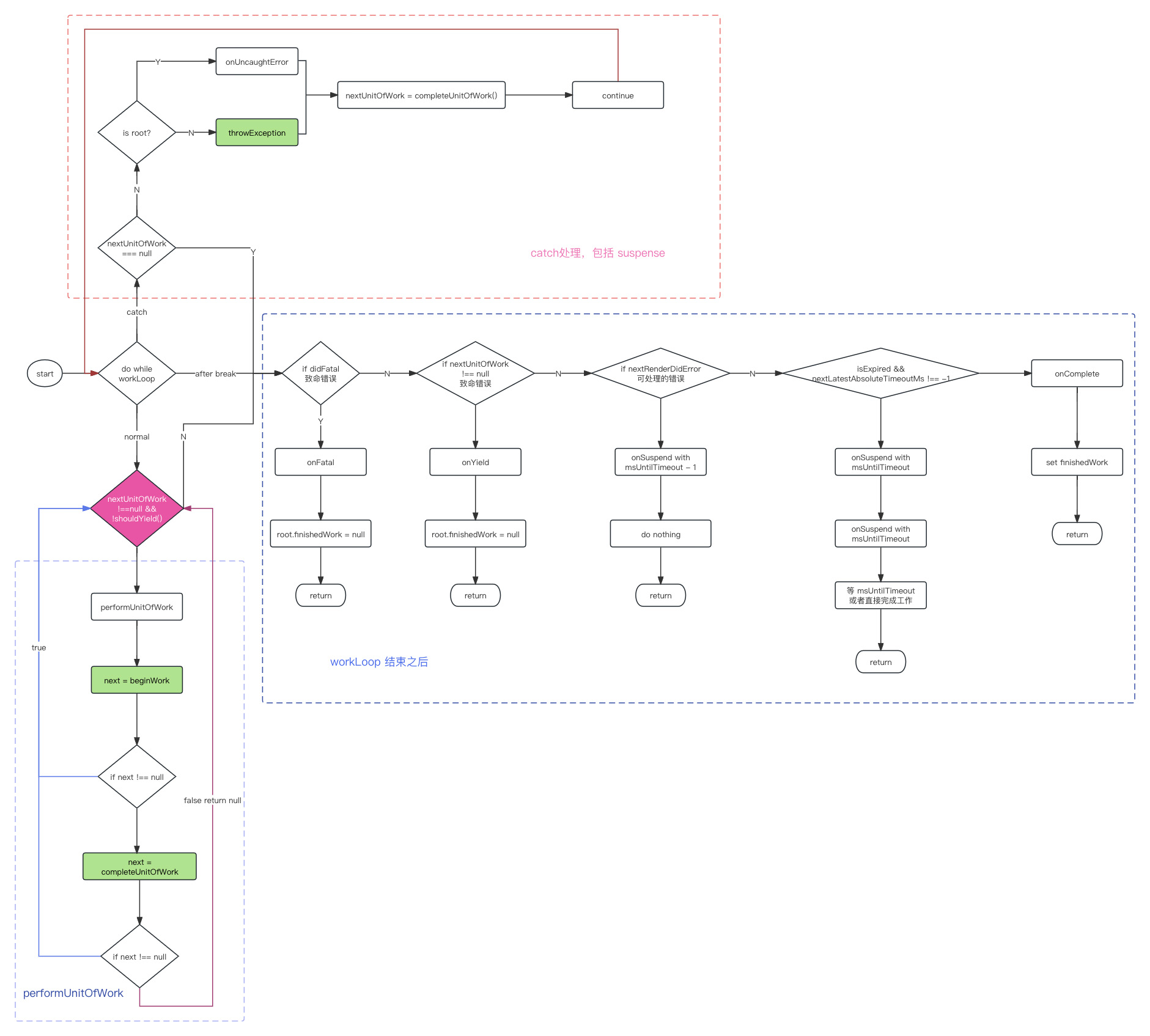
React16源码: React中的renderRoot的源码实现
renderRoot 1 )概述 renderRoot 是一个非常复杂的方法这个方法里处理很多各种各样的逻辑, 它主要的工作内容是什么?A. 它调用 workLoop 进行循环单元更新 遍历整个 Fiber Tree,把每一个组件或者 dom 节点对应的Fiber 节点拿出来单一的进行更…...
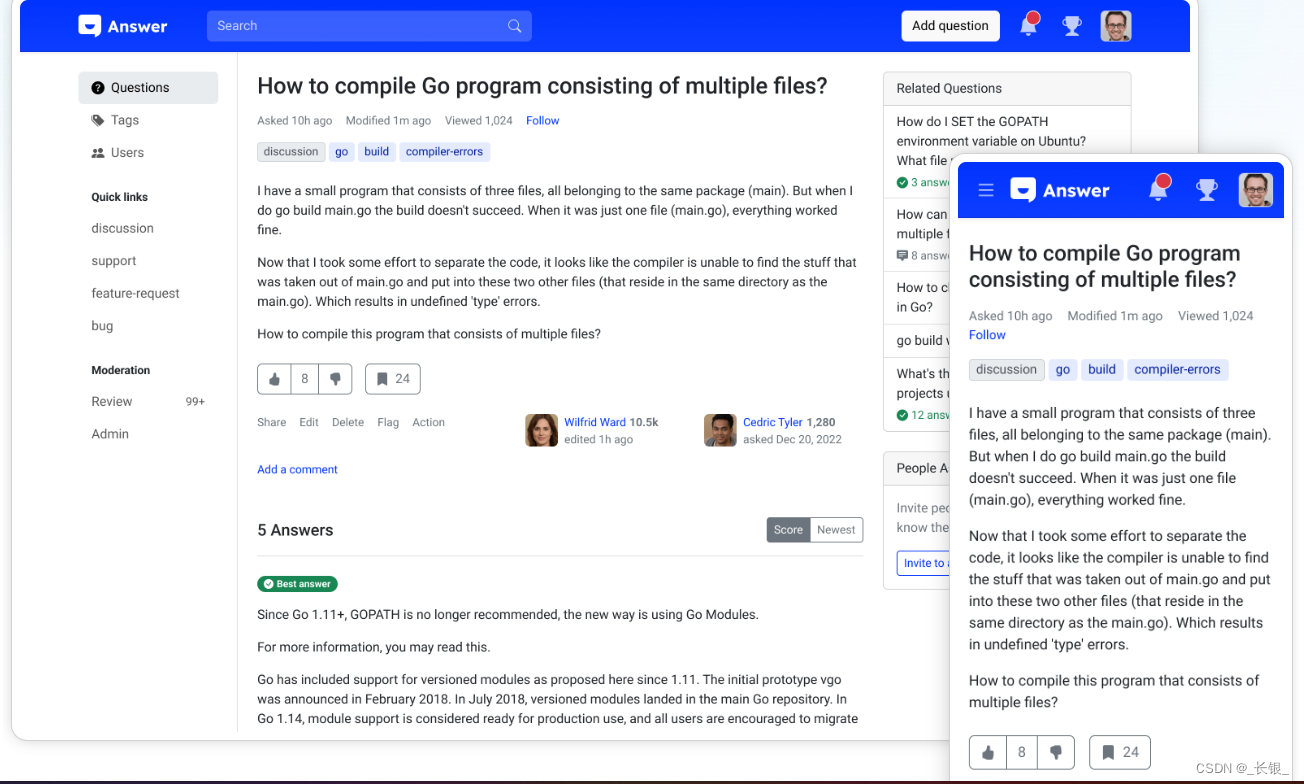
GitHub项目推荐-incubator
项目地址 Github地址:GitHub - apache/incubator-anser 官网:Apache Answer | Free Open-source Q&A Platform 项目简述 这是Apache的一个开源在线论坛,也可以部署成为一个自有的QA知识库。项目主要使用了Go和Typescript来开发&#…...

如何使用ActiveMQ
ActiveMQ是Apache的一款开源消息总线,主要用来做消息的分发。使用ActiveMQ,通常需要以下步骤: 一、启动ActiveMQ 首先需要下载ActiveMQ,然后进行启动。启动后,可以在控制台创建队列,初始用户名和密码通常…...

《Python 3 基础》- numpy的array,python的list、tuple的区别与联系再辨析
这里写自定义目录标题 一、基本认识二、list与传统数组(以C为例)的联系与区别三、1维list切片规则四、2维list类似于2维数组,但表达方式需适应五、list与元组的联系与区别1. tuple的创建方法类似于list,tuple用(&#…...

写点东西《最佳 Web 框架不存在 》
写点东西《🥇最佳 Web 框架不存在 🚫》 TLDR;您选择的 Web 应用程序框架并不重要。嗯,它很重要,但并不像其他人希望您相信的那样重要。 2024 年存在如此多的库和框架,而且最好的库和框架仍然备受争议&…...
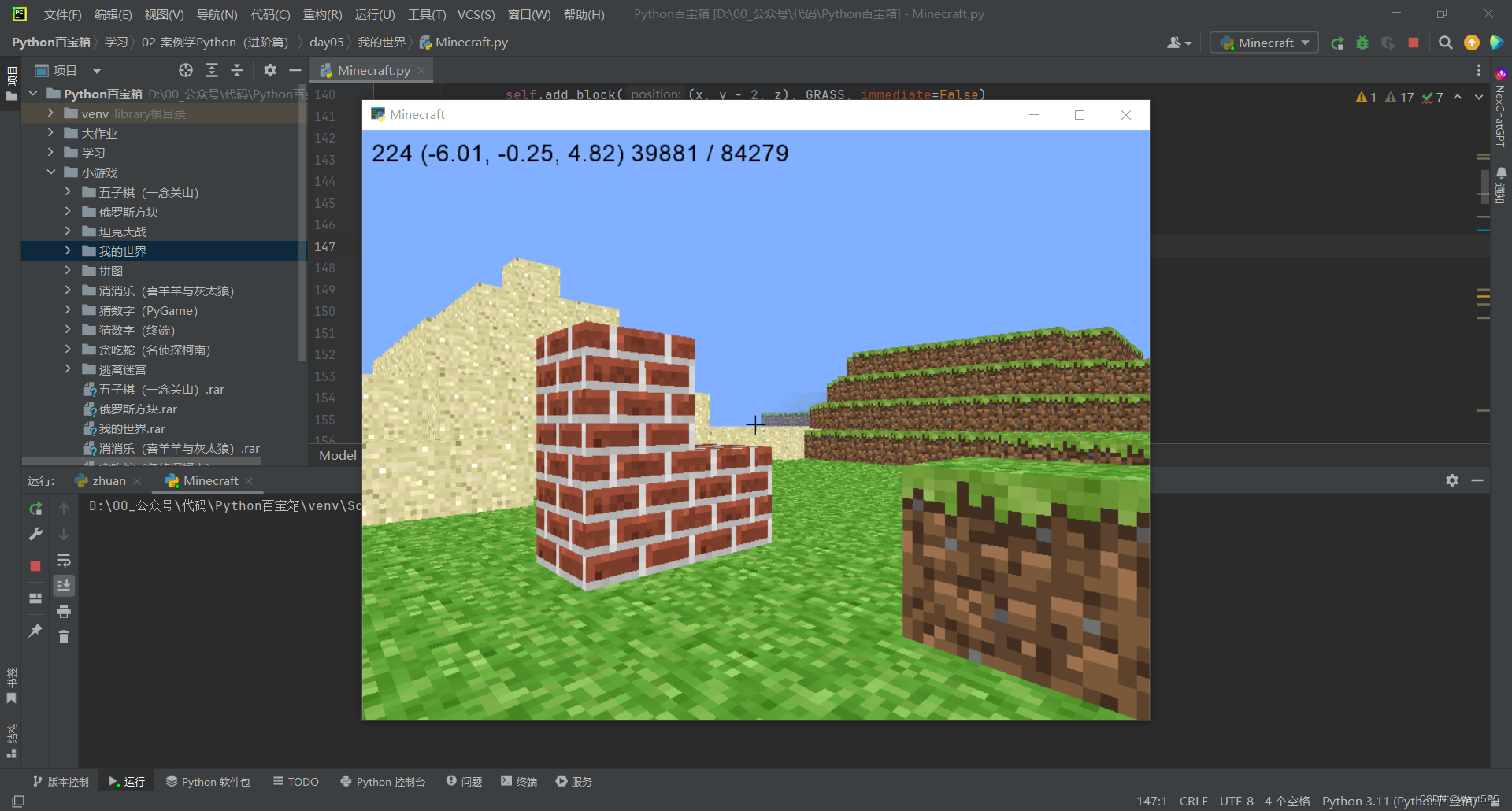
游戏开发丨基于PyGlet的简易版Minecraft我的世界游戏
文章目录 写在前面我的世界PyGlet简介实验内容游戏按键程序设计引入文件 运行结果写在后面 写在前面 本期内容:基于PyGlet的简易版Minecraft我的世界游戏 实验环境: pycharmpyglet 项目下载地址:https://download.csdn.net/download/m0_6…...

在线的货币兑换平台源码下载
在线的货币兑换平台,可帮助全球各地的个人和企业将货币从一种货币兑换为另一种货币。该货币兑换平台是 Codecanyon 中最先进的脚本。 源码下载:https://download.csdn.net/download/m0_66047725/88728084...
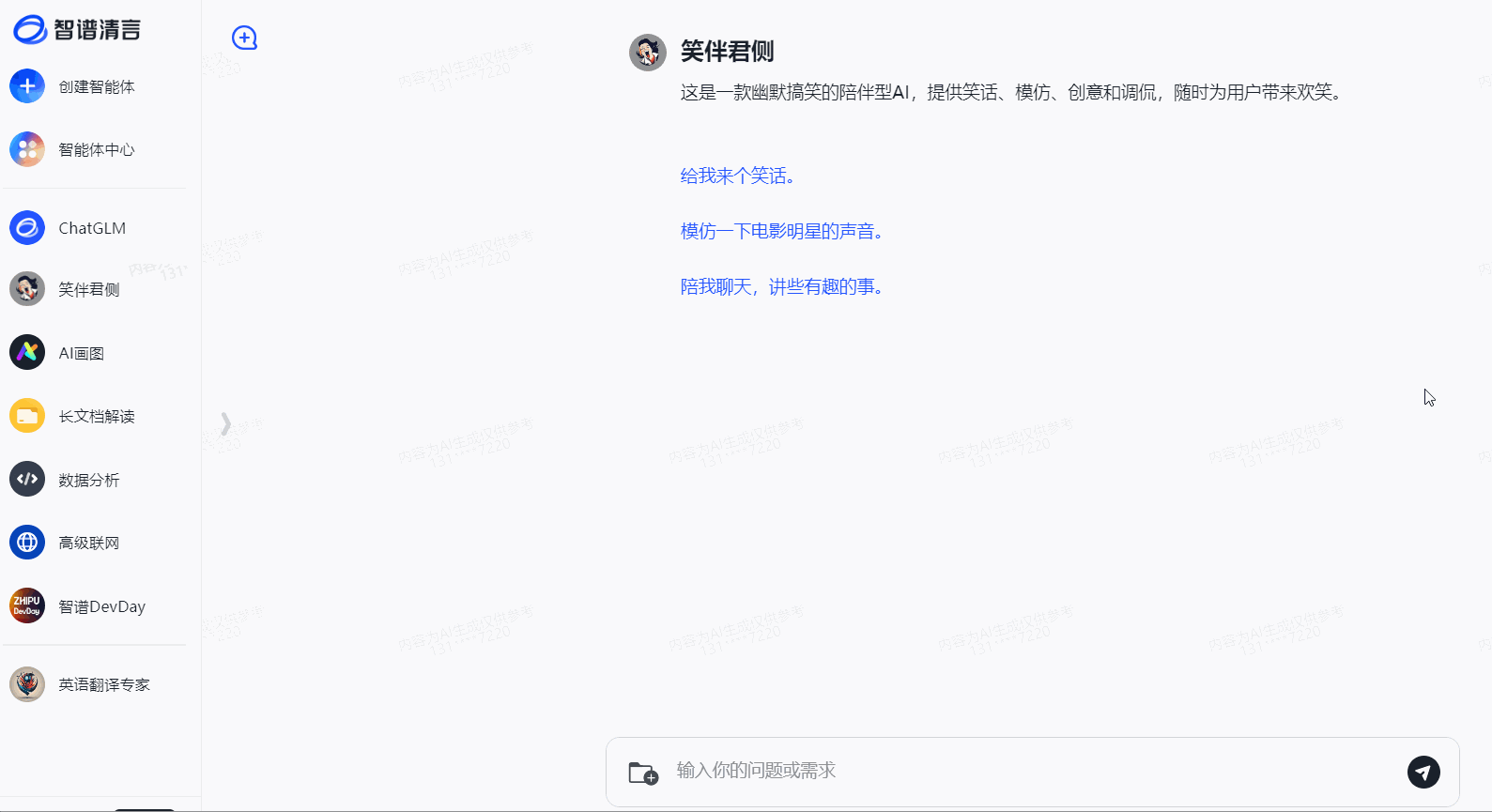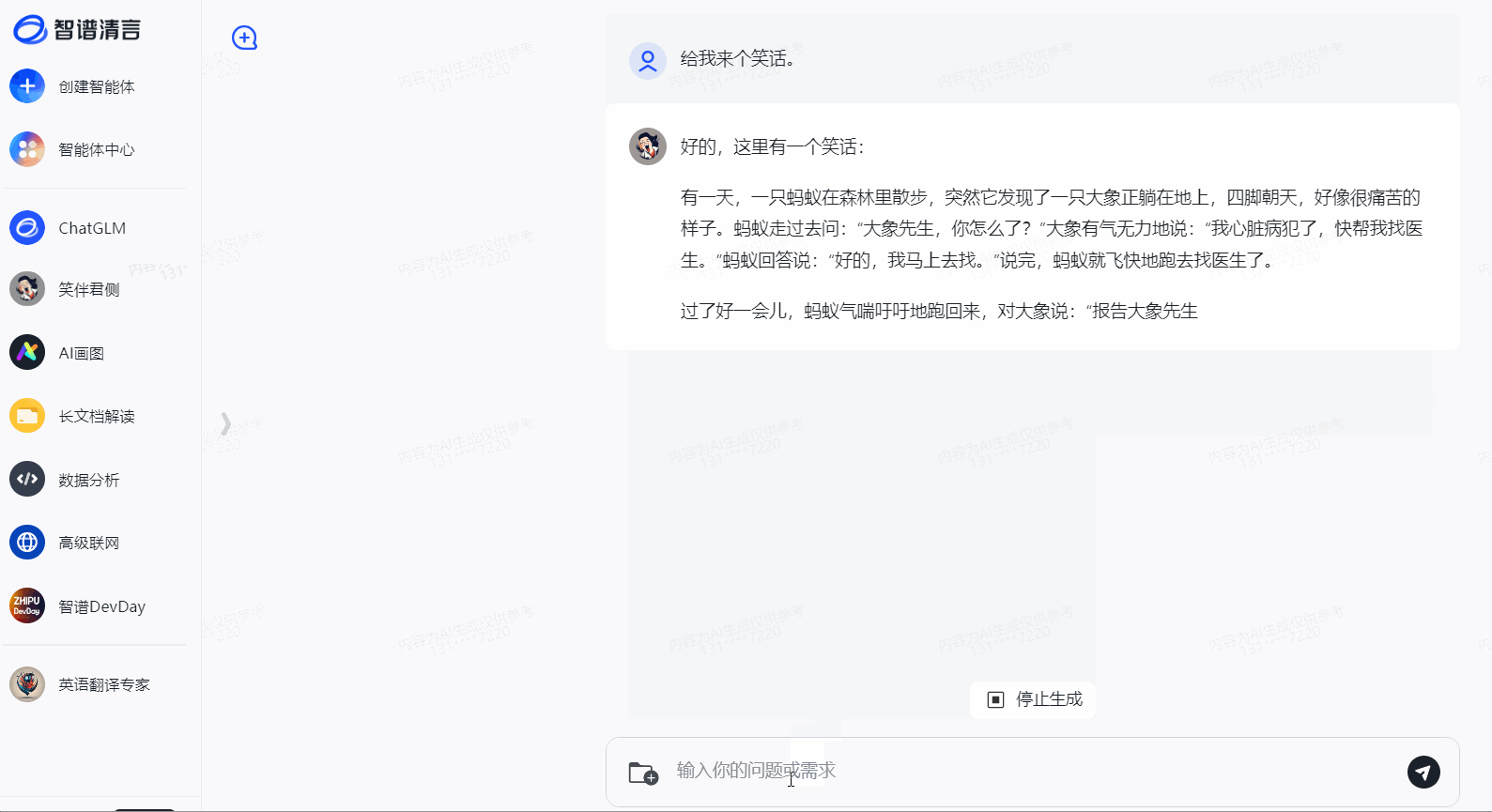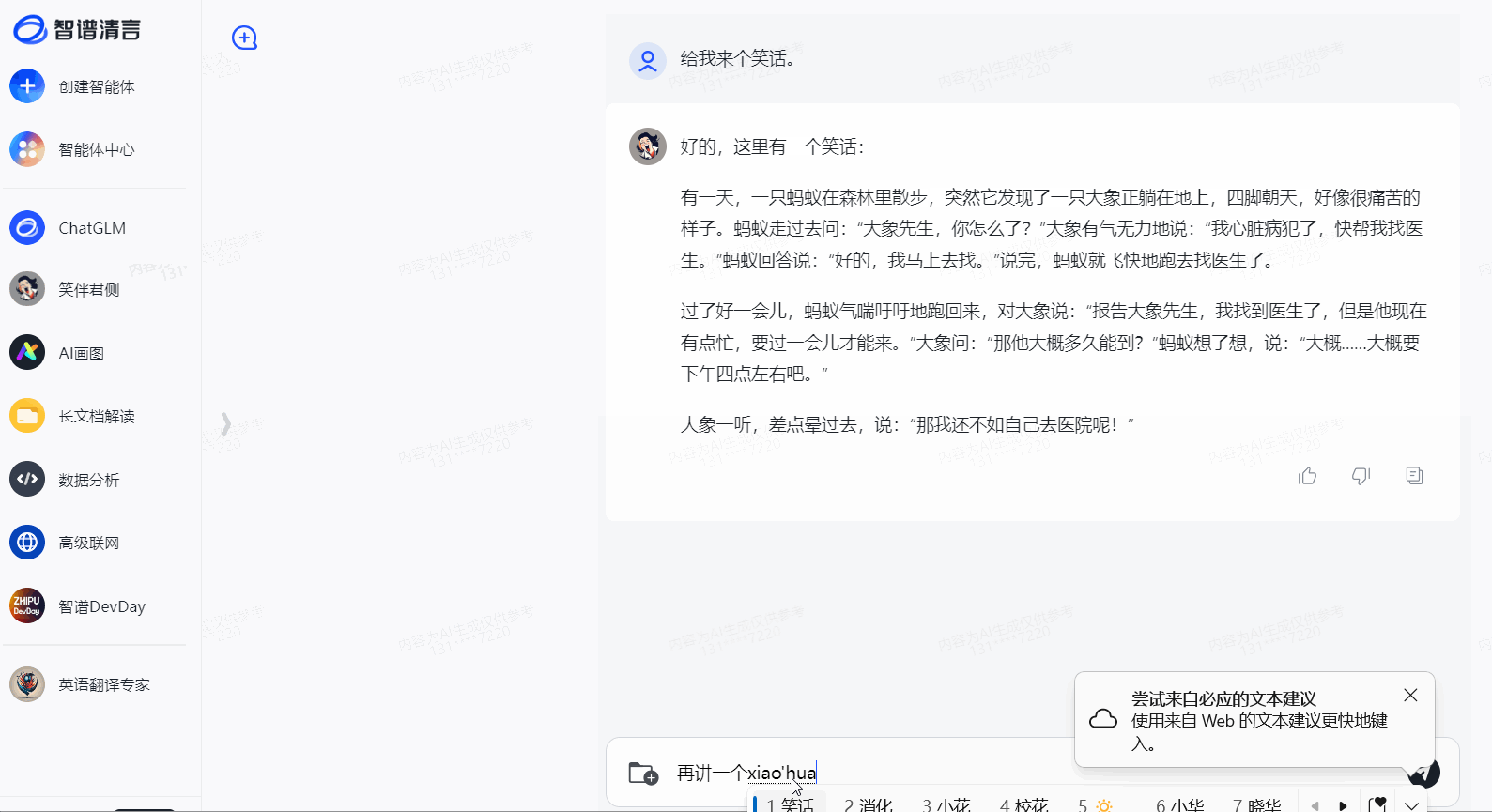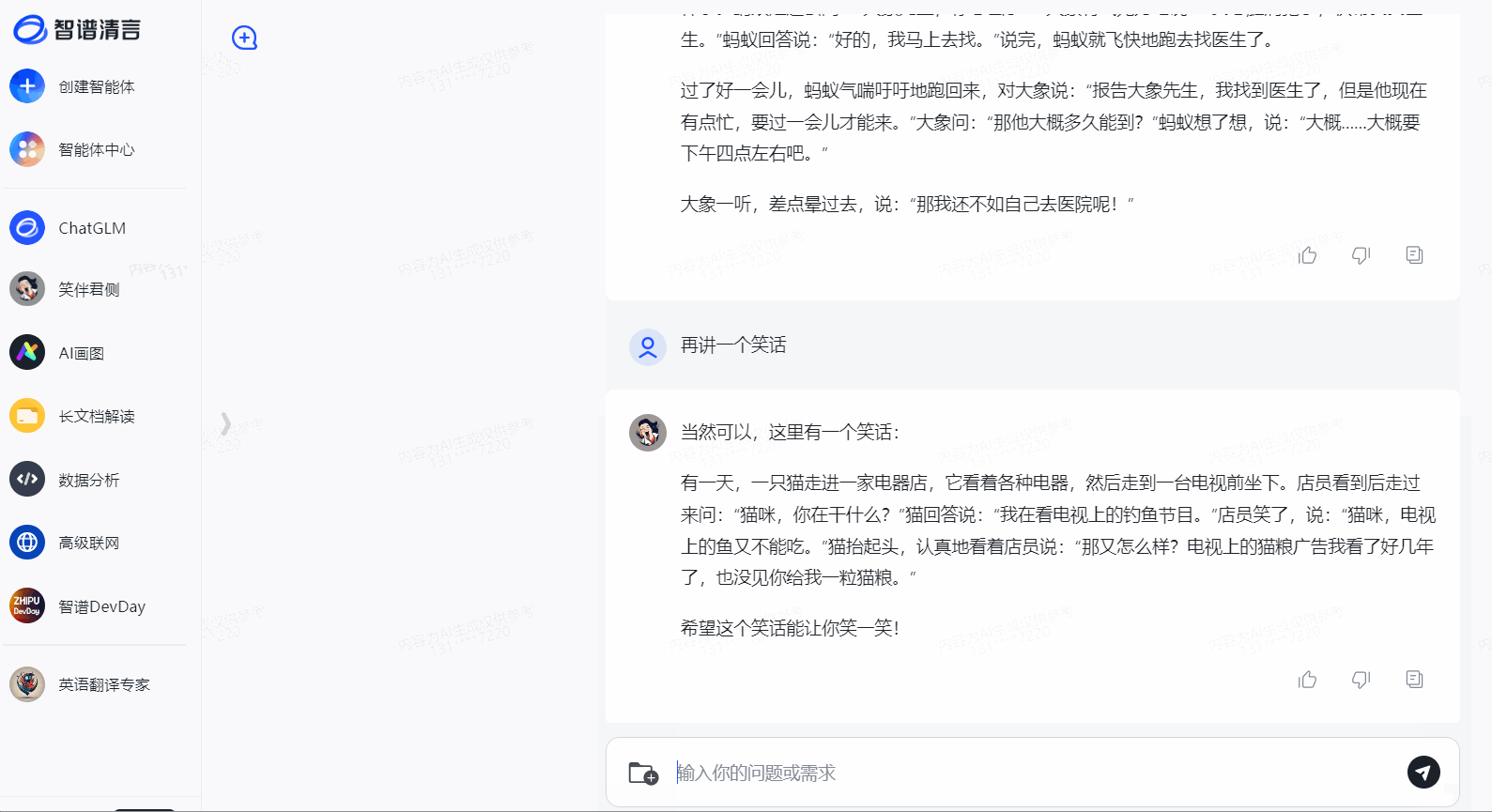
LLMs之GLM-4:GLM-4的简介、安装和使用方法、案例应用之详细攻略
LLMs之GLM-4:GLM-4的简介、安装和使用方法、案例应用之详细攻略 导读:2024年01月16日,智谱AI在「智谱AI技术开放日(Zhipu DevDay)」推出新一代基座大模型GLM-4。GLM-4 的主要亮点和能力如下:>> 性能与GPT-4相近:多模态、长文…...
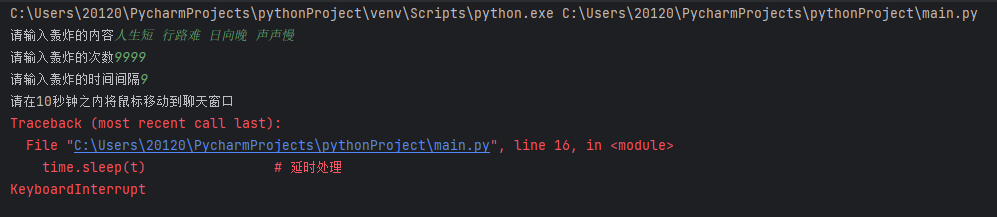
用Python“自动连发消息”
自动连发消息,基本上C和Python的思路都是不停的模拟“击键”操作,还有一种VB的脚本写法,反成每种语言都能写,更厉害的可以用java做出个GUI界面,先上代码。 一 代码 import pyautogui # 鼠标 import p…...

CSS3中多列布局详解
多列布局 概念:在CSS3之前,想要设计类似报纸那样的多列布局,有两种方式可以实现:一种是"浮动布局",另一种是“定位布局”。 这两种方式都有缺点:浮动布局比较灵活,但不容易控制&…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...
Element-Plus:popconfirm与tooltip一起使用不生效?
你们好,我是金金金。 场景 我正在使用Element-plus组件库当中的el-popconfirm和el-tooltip,产品要求是两个需要结合一起使用,也就是鼠标悬浮上去有提示文字,并且点击之后需要出现气泡确认框 代码 <el-popconfirm title"是…...
