动态规划思想案例刨析
动态规划的思想
动态规划解决问题的核心思想是“重叠子问题”和“最优子结构”。
重叠子问题:在复杂问题中,往往存在许多重复的子问题。动态规划通过避免重复计算,将子问题的解保存起来,以便在需要时直接引用,从而提高效率。通过记忆化存储或者使用动态规划表来实现。
最优子结构:如果一个问题的最优解包含了其子问题的最优解,那么我们称这个问题具有最优子结构。动态规划利用最优子结构的性质,将问题划分为一系列规模较小的子问题,通过求解子问题的最优解来得到原问题的最优解。
动态规划的应用步骤
使用动态规划解决问题一般包括以下步骤:
-
定义状态:明确问题的状态,即问题的子问题是什么,以及如何表示子问题的状态。状态的选择通常与问题的特性相关。
-
确定状态转移方程:根据问题的最优子结构,确定子问题之间的关系,即如何通过子问题的最优解来求解原问题的最优解。这个关系可以用状态转移方程来表示。
-
确定初始条件和边界情况:确定初始状态和边界情况,即最简单的子问题的解。
-
计算顺序:确定计算子问题的顺序,通常是自底向上或者自顶向下的方式。
-
计算最优解:根据状态转移方程和初始条件,计算子问题的最优解,并逐步计算得到原问题的最优解。
动态规划的应用案例
动态规划可以应用于各种问题领域,如:
- 背包问题:0-1背包问题、完全背包问题等。
- 最短路径问题:迪杰斯特拉算法、弗洛伊德算法等。
- 编辑距离问题:计算两个字符串之间的最小编辑操作次数。
- 斐波那契数列:通过动态规划的方式计算斐波那契数列的第n项。
- 矩阵链乘法:计算矩阵相乘的最优顺序。
具体代码分析
1. 背包问题(Knapsack Problem):
背包问题是一个经典的优化问题,可以分为01背包问题和完全背包问题。这里以01背包问题为例,即每个物品只能选择放入背包一次或不放入。
1,动态规划解决01背包问题的代码示例:
public class KnapsackProblem {public static int knapsack(int[] weights, int[] values, int capacity) {int n = weights.length;int[][] dp = new int[n + 1][capacity + 1];// 初始化第一行和第一列为0,表示没有物品或容量为0时的最大价值为0for (int i = 0; i <= n; i++) {dp[i][0] = 0;}for (int j = 0; j <= capacity; j++) {dp[0][j] = 0;}// 动态规划求解for (int i = 1; i <= n; i++) {for (int j = 1; j <= capacity; j++) {if (weights[i - 1] <= j) {// 当前物品的重量小于等于背包容量,可以选择放入或不放入背包dp[i][j] = Math.max(values[i - 1] + dp[i - 1][j - weights[i - 1]], dp[i - 1][j]);} else {// 当前物品的重量大于背包容量,不能放入背包dp[i][j] = dp[i - 1][j];}}}return dp[n][capacity];}public static void main(String[] args) {int[] weights = {2, 3, 4, 5};int[] values = {3, 4, 5, 6};int capacity = 8;int maxVal = knapsack(weights, values, capacity);System.out.println("背包能够装下的最大价值为:" + maxVal);}
}
代码解释:
weights数组存储物品的重量,values数组存储物品的价值,capacity表示背包的容量。dp是一个二维数组,dp[i][j]表示前i个物品在背包容量为j时的最大价值。- 动态规划的核心思想是通过填充
dp数组来逐步计算最优解。 - 外部两层循环用于遍历每个物品和每个背包容量。
- 内部的条件判断根据当前物品的重量,决定是否放入背包以获得最大价值。
- 最终返回
dp[n][capacity],即前n个物品在背包容量为capacity时的最大价值。
完全背包问题是一个经典的动态规划问题,它可以描述为在给定背包容量和一组物品的情况下,选择物品放入背包,使得背包中物品的总价值最大化。与0-1背包问题不同的是,完全背包问题中每个物品可以选择无限次放入背包。
2,完全背包问题的动态规划求解方法:
假设有N个物品,它们的重量分别为w[1], w[2], …, w[N],价值分别为v[1], v[2], …, v[N],背包的容量为C。我们定义一个二维数组dp[N+1][C+1],其中dp[i][j]表示在前i个物品中选择,且背包容量为j时的最大总价值。
初始化dp数组中的所有元素为0。然后我们从前往后遍历物品,对于每个物品i,从容量0到C依次计算dp[i][j]的值。
对于dp[i][j]的计算,有两种情况:
- 不选择当前物品i:dp[i][j] = dp[i-1][j],即背包容量为j时,前i个物品的最大总价值与前i-1个物品的最大总价值相同。
- 选择当前物品i:dp[i][j] = dp[i][j-w[i]] + v[i],即背包容量为j时,考虑物品i放入背包,此时总价值为dp[i][j-w[i]](在当前物品i的基础上减去物品i的重量w[i],背包容量减少),再加上物品i的价值v[i]。
综合以上两种情况,dp[i][j]的最大值即为dp[i-1][j]和dp[i][j-w[i]] + v[i]的较大值。
最终,dp[N][C]即为问题的解,表示在前N个物品中选择,且背包容量为C时的最大总价值。
以下是完全背包问题的代码示例(使用Java语言):
public class Knapsack {public static int knapsack(int[] weights, int[] values, int capacity) {int n = weights.length;int[][] dp = new int[n + 1][capacity + 1];for (int i = 1; i <= n; i++) {for (int j = 1; j <= capacity; j++) {if (weights[i - 1] <= j) {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - weights[i - 1]] + values[i - 1]);} else {dp[i][j] = dp[i - 1][j];}}}return dp[n][capacity];}public static void main(String[] args) {int[] weights = {2, 3, 4, 5};int[] values = {3, 4, 5, 6};int capacity = 8;int maxTotalValue = knapsack(weights, values, capacity);System.out.println("背包中物品的最大总价值为:" + maxTotalValue);}
}
这个示例代码中,weights数组和values数组分别表示物品的重量和价值,capacity表示背包的容量。最后输出的maxTotalValue即为背包中物品的最大总价值。
2. 打家劫舍问题(House Robber Problem):
打家劫舍问题是一个经典的动态规划问题,可以形象地描述为在一条街上的房屋中选择一些房屋进行盗窃,但不能同时盗窃相邻的房屋。目标是盗窃到的金额最大。
以下是用动态规划解决打家劫舍问题的代码示例:
public class HouseRobber {public static int rob(int[] nums) {int n = nums.length;if (n == 0) {return 0;}if (n == 1) {return nums[0];}int[] dp = new int[n];dp[0] = nums[0];dp[1] = Math.max(nums[0], nums[1]);for(int i = 2; i < n; i++) {dp[i] = Math.max(nums[i] + dp[i - 2], dp[i - 1]);}return dp[n - 1];}public static void main(String[] args) {int[] nums = {1, 2, 3, 1};int maxAmount = rob(nums);System.out.println("能够盗窃到的最大金额为:" + maxAmount);}
}
代码解释:
nums数组存储每个房屋中的金额。dp数组存储从第一个房屋到当前房屋的最大金额。- 初始化
dp[0]为第一个房屋的金额,dp[1]为第一个和第二个房屋中金额较大的一个。 - 从第三个房屋开始,每次选择盗窃当前房屋和前两个房屋中金额较大的一个,将结果存入
dp[i]。 - 最终返回
dp[n - 1],即最后一个房屋的最大金额。
3. 最长递增子序列(Longest Increasing Subsequence):
最长递增子序列问题是要找到给定序列中的最长递增子序列的长度。以下是用动态规划解决最长递增子序列问题的代码示例:
public class LongestIncreasingSubsequence {public static int lengthOfLIS(int[] nums) {int n = nums.length;int[] dp = new int[n];Arrays.fill(dp, 1);for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) {dp[i] = Math.max(dp[i], dp[j] + 1);}}}int maxLength = 0;for (int len : dp) {maxLength = Math.max(maxLength, len);}return maxLength;}public static void main(String[] args) {int[] nums = {10, 9, 2, 5, 3, 7, 101, 18};int maxLength = lengthOfLIS(nums);System.out.println("最长递增子序列的长度为:" + maxLength);}
}
代码解释:
nums数组存储给定的序列。dp数组用于记录每个位置上的最长递增子序列长度,初始值都为1。- 外部两层循环用于遍历每个位置,并比较当前位置与之前位置的大小关系。
- 如果当前位置的值大于之前位置的值,则更新当前位置上的最长递增子序列长度为之前位置中最大长度加1。
- 最终返回
dp数组中的最大值,即为最长递增子序列的长度。
4. 矩阵连乘积问题(Matrix Chain Multiplication):
矩阵连乘积问题是一个经典的动态规划问题,要求找到一种最优的矩阵相乘顺序,使得整个连乘的计算量最小。以下是用动态规划解决矩阵连乘积问题的代码示例:
public class MatrixChainMultiplication {public static int matrixChainOrder(int[] dimensions) {int n = dimensions.length - 1;int[][] dp = new int[n][n];for (int len = 2; len <= n; len++) {for (int i = 0; i < n - len + 1; i++) {int j = i + len - 1;dp[i][j] = Integer.MAX_VALUE;for (int k = i; k < j; k++) {int cost = dp[i][k] + dp[k + 1][j] + dimensions[i] * dimensions[k + 1] * dimensions[j + 1];if (cost < dp[i][j]) {dp[i][j] = cost;}}}}return dp[0][n - 1];}public static void main(String[] args) {int[] dimensions = {10, 30, 5, 60};int minCost = matrixChainOrder(dimensions);System.out.println("最小的矩阵连乘积计算量为:" + minCost);}
}
代码解释:
dimensions数组存储矩阵的维度信息,如[10, 30, 5, 60]表示有三个矩阵,维度分别为10x30、30x5和5x60。dp数组用于记录每个子问题的最小计算量。- 外部两层循环用于遍历子问题的长度,从2开始逐步增加。
- 内部的循环用于遍历每个子问题的起始位置和结束位置,并计算当前情况的最小计算量。
- 在内部循环中,通过尝试不同的划分点,计算出将两个子问题相乘的计算量,并选择最小的计算量作为当前子问题的最优解。
- 最终返回
dp[0][n - 1],即整个矩阵连乘的最小计算量。
总结
动态规划是一种将复杂问题化繁为简的求解方法。通过将问题划分为一系列子问题,并通过求解子问题的最优解来得到原问题的最优解。动态规划的核心思想是重叠子问题和最优子结构。通过定义状态、确定状态转移方程、确定初始条件和边界情况、计算顺序以及计算最优解这几个步骤,我们可以有效地应用动态规划解决各种问题。
相关文章:

动态规划思想案例刨析
动态规划的思想 动态规划解决问题的核心思想是“重叠子问题”和“最优子结构”。 重叠子问题:在复杂问题中,往往存在许多重复的子问题。动态规划通过避免重复计算,将子问题的解保存起来,以便在需要时直接引用,从而提…...
vtk9.3 配置 visual studio 2019 运行环境 和运行实例详解
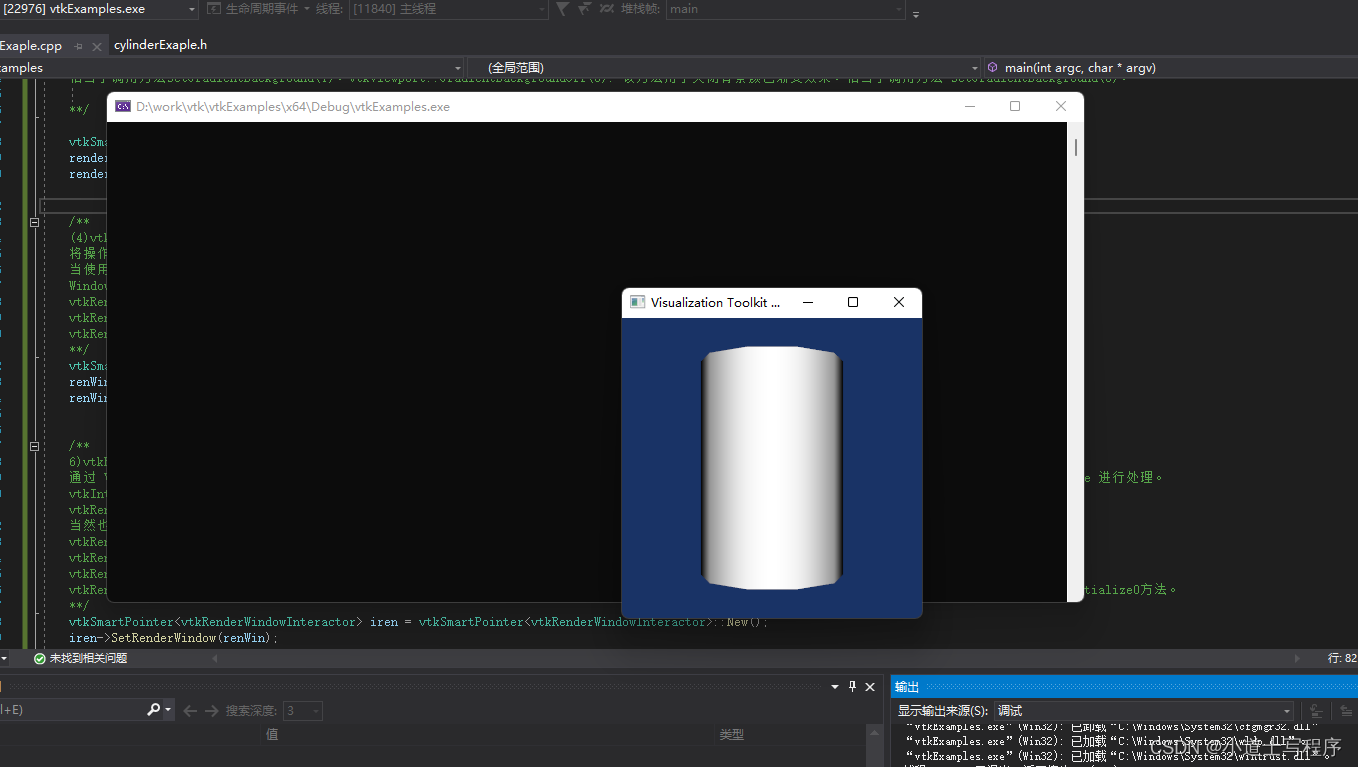
(1)包含文件配置: 项目--属性--VC目录,在包含目录中把include文件夹的地址加进去,一直要到下一级 vtk-9.3目录下, 小知识: 在Visual Studio 2019中运行项目时,如果项目中使用了第三…...
腾讯云添加SSL证书
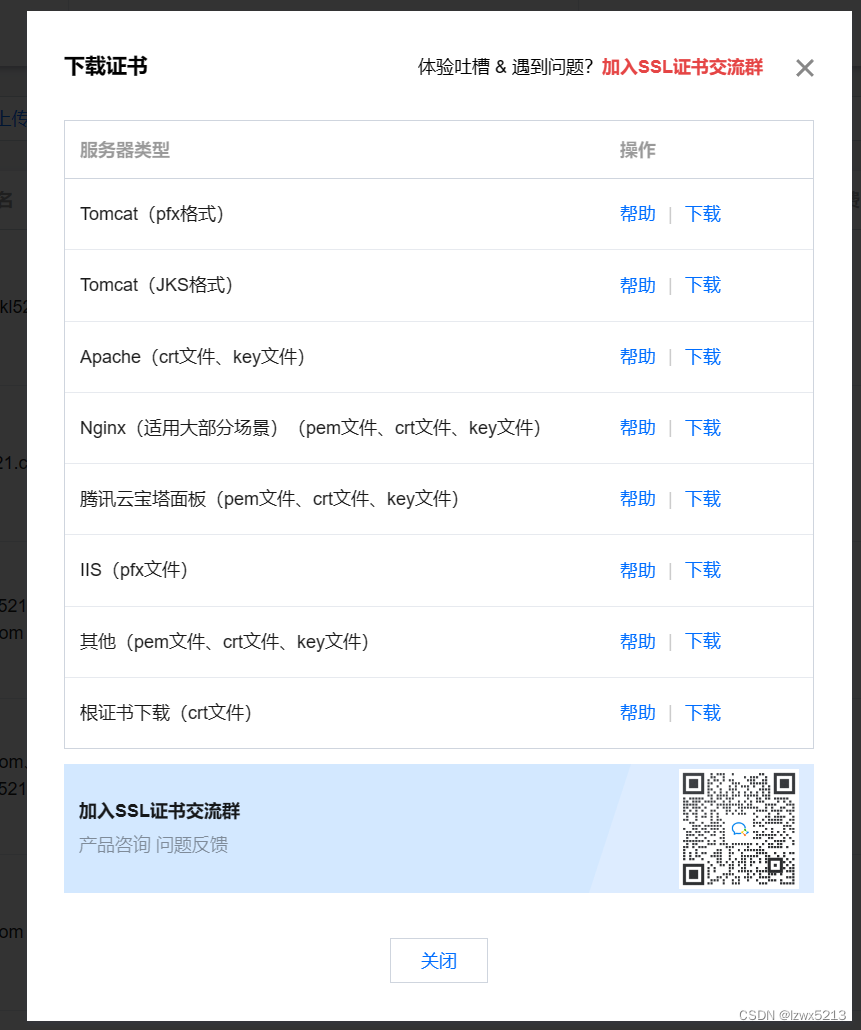
一、进入腾讯云SSL证书: ssl证书控制台地址 选择“我的证书”,点击"申请免费证书" 2、填写域名和邮箱,点击“提交申请” 在此页面中会出现主机记录和记录值。 2、进入云解析 DNS:云解析DNS地址 进入我的解析-记录…...

CentOS下用rpm安装软件时报错error: Failed dependencies
在CentOS下用rpm安装软件时会报如下错误: 1、安装时提示: [rootdb software]# rpm -ivh ksh-20120801-254.el8.x86_64.rpm warning: ksh-20120801-254.el8.x86_64.rpm: Header V3 RSA/SHA256 Signature, key ID 8483c65d: NOKEY error: Failed depende…...
Vue3+Vite连接高德地图JS API——地图显示、输入搜索
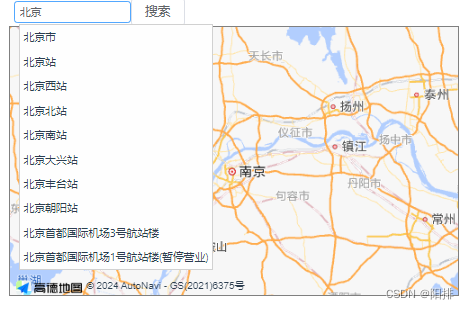
1 开通高德地图Web端JS API服务 1、进入高德地图API官网(https://lbs.amap.com/): 2、注册登录。 3、进入控制台。 4、点击“应用管理”,点击“我的应用”,创建新应用。 5、添加Key,服务平台选择“Web端&…...
一台java服务器可以跑多少个线程?
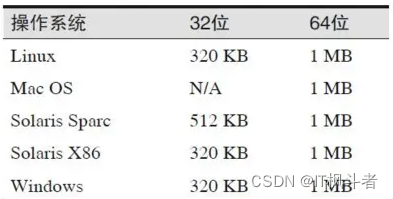
一台java服务器可以跑多少个线程? 一台java服务器能跑多少个线程?这个问题来自一次线上报警如下图,超过了我们的配置阈值。 打出jstack文件,通过IBM Thread and Monitor Dump Analyzer for Java工具查看如下: 共计166…...

【Python 千题 —— 基础篇】猜数字小游戏
题目描述 题目描述 猜数字。利用 random 函数随机生成一个1~100之间的数并存储在变量中,然后使用条件判断以及循环方式编写一个猜数字的环节: 如果输入的数字大于随机生成的数字,则输出“猜大了”如果输入的数字小于随机生成的数字&#x…...

Android Media3 ExoPlayer 如何正确设置缓存大小
在播放音视频时,如何开启 Android Media3 ExoPlayer 缓存,请参考笔者另外一篇文章: Android Media3 Exoplayer 开启缓存功能 笔者在设置 ExoPlayer 的缓存大小时,遇到一个非常奇怪的问题,例如,设置最大缓存…...

WPF实现右键选定TreeViewItem
在WPF中,TreeView默认情况是不支持右键选定的,也就是说,当右键点击某节点时,是无法选中该节点的。当我们想在TreeViewItem中实现右键菜单时,往往希望在弹出菜单的同时选中该节点,以使得菜单针对选中的节点生…...

蓝桥杯 java 重复字符串
题目描述 * 如果一个字符串S恰好可以由某个字符串重复K次得到,我们就称S是K次重复字符串。 * 例如 abcabcabc 可以看作是 abc重复3次得到,所以 abcabcabc 是3次重复字符串。 * 同理 aaaaaa 既是2次重复字符串、又是3次重复字符串和6次重复字符串。 * 现在…...

Vue实战:两种方式创建Vue项目
文章目录 一、实战概述二、实战步骤(一)安装Vue CLI脚手架1、从Node.js官网下载LTS版本2、安装Node.js到指定目录3、配置Node.js环境变量4、查看node版本5、查看npm版本6、安装Vue Cli脚手架7、查看Vue Cli版本 (二)命令行方式构建…...

不同打包工具下的环境变量配置方式对比
本文作者为 360 奇舞团前端开发工程师 天明 前言 在现代的JavaScript应用程序开发中,环境变量的配置是至关重要的。不同的应用场景和部署环境可能需要不同的配置,例如开发、测试和生产环境。最常见的需求是根据不同的环境,配置如是否开启sour…...
5个99%的人可能不知道的实用程序库!
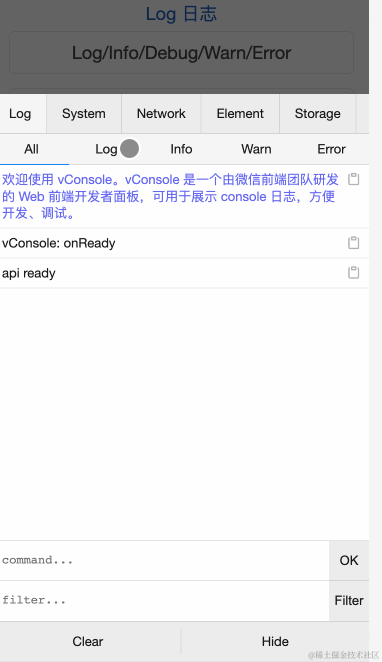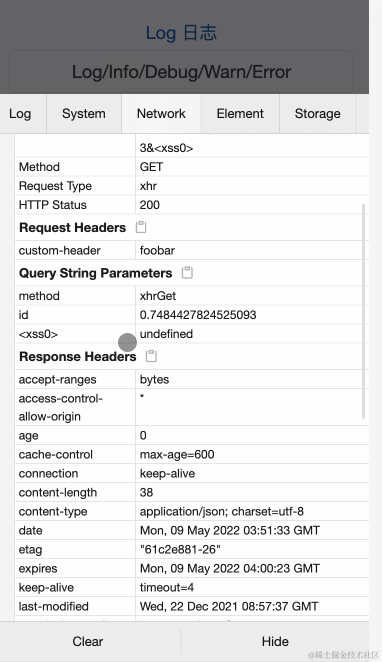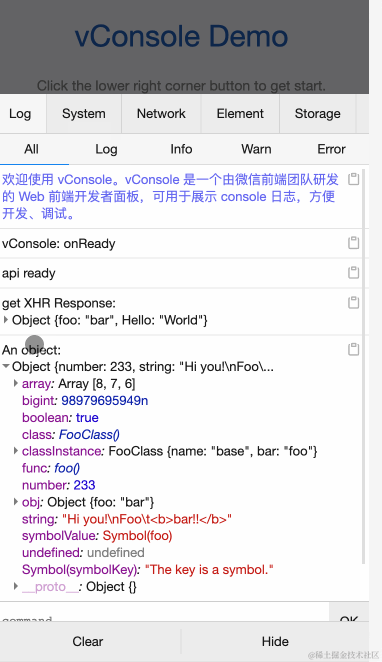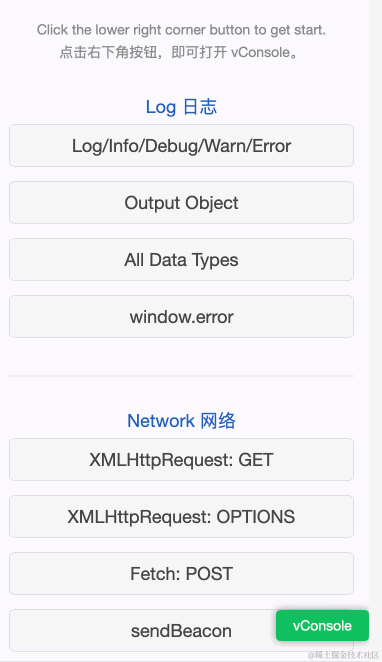
前言 作为一名前端开发者,这些 JavaScript 库极大地提高了我的工作效率,如格式化日期、处理 URL 参数和调试移动网页。朋友们,我想和你们分享这些库。 1. 使用 “Day.js” 来格式化日期和时间 链接 作为开发者,我已经厌倦了在 JavaScript 中操作日期和时间,因为它太麻烦了。…...

shell脚本,ADB
Linux命令行命令是系统内置的命令或用户自定义的脚本(shell 脚本,.sh扩展名结尾),可以通过终端输入命令来执行。这些命令通常存储在Linux系统的/bin、/usr/bin、/sbin、/usr/sbin等目录下,也可以在$PATH环境变量中指定…...

微服务治理:微服务安全详解
微服务安全旨在保护微服务架构中每一个独立的服务。与传统单体应用程序不同,它们在单点应用安全措施,微服务由于其独立性,需要分布式安全方法。 为何关注微服务安全? 攻击面扩大: 更多服务暴露在外,意味着攻击者拥有…...
迅为RK3588开发板编译 Buildroot单独编译图形化界面三
第三步:编译 Recovery 首先在 linux 源码目录下输入以下命令进入编译的 UI 界面,进入之后如下所示: ./build.sh 然后将光标移动到第四个 recovery,点击回车即可开始 recovery 的编译,编译过程如下所示: 编…...

yum仓库及NFS共享
目录 一.yum仓库的基本原理 1.Yum概述: 2.Yum实现过程: 二. yum配置文件及命令: 1. 主配置文件: 2. 仓库设置文件: 3 .日志文件: 编辑4.yum命令详解: 三. 搭建仓库的方式: …...
【Web】CTFSHOW PHP特性刷题记录(全)
知其然知其所以然,尽量把每种特性都详细讲明白。 目录 web89 web90 web91 web92 web93 web94 web95 web96 web97 web98 web99 web100 web101 web102 web103 web104 web105 web106 web107 web108 web109 web110 web111 web112 web113 web…...
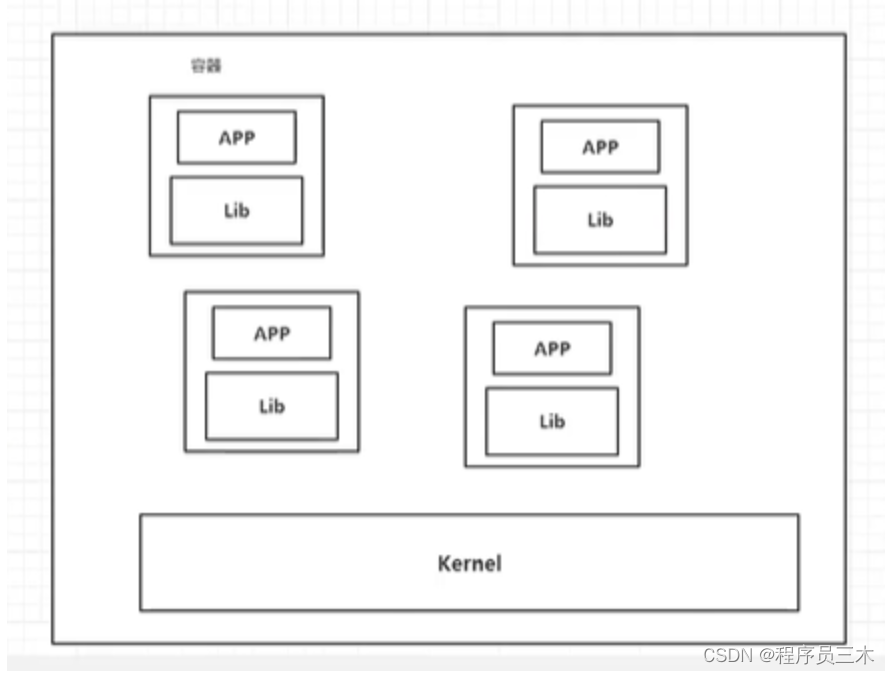
[Docker] Docker为什么出现
Docker为什么出现 一款产品: 开发–上线 -->两套环境 | 应用配置 开发即运维! 环境配置十分麻烦,每一个机器都要部署环境(Redis, ES, Hadoop) 费时费力 项目带上配置环境安装打包。 传统: 开发jar&…...

小程序基础学习(页面跳转传参)
目录 正向传参 原理:直接在url里面拼接参数即可 接受参数 编辑 已经跳转到的页面用onLoad函数来接受即可然后写回页面展示即可 逆向传参 原理:通过使用 getCurrentPages()这个方法来获取返回页面列表,然后再用页面.setDataÿ…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...
