itextpdf 之 html 转 pdf 问题处理
相关文章：
itextpdf 之 html 转 pdf 问题处理
1. Font Provider contains zero fonts. At least one font shall be present 此问题出现的原因是 字体设置不成功，解决方法就是排查设置字体的代码。 需要特别注意的是项目打包后项目中所有文件层次会出现变动，使用何种方式获取字体文件会直接影响到字…...
关于tex中的表格设置
文章目录 控制表格列宽和行高控制表格列宽的同时实现居中tex中多表格排列单元格的合并与分割对单个单元格进行操作 控制表格列宽和行高 将下面的代码放在table环境内，放在tabular环境外 调整表格宽度和高度： \resizebox{\textwidth}{2cm}{%第一个{}是表…...
huggingface学习 | 云服务器使用git-lfs下载huggingface上的模型文件
文章目录 一、找到需要下载的huggingface文件二、准备工作（一）安装git-lfs（二） 配置git ssh 三、检查ssh连接huggingface是否成功 一、找到需要下载的huggingface文件 huggingface官网链接：https://huggingface.co/ 以…...
使用C++读取SQL Server数据库中的数据并转换为UNICODE类型
要使用C读取SQL Server数据库中的数据并转换为UNICODE类型，可以使用ODBC库和UNICODE编码函数。 首先，确保已安装SQL Server的ODBC驱动程序，并在项目中包含ODBC头文件<sql.h>和<sqlext.h>。 接下来，可以按照以下步骤进…...
WPF应用程序生存期以及相关事件
WPF 应用程序的生存期会通过 Application 引发的几个事件来加以标记，相关事件对应着应用程序何时启动、激活、停用和关闭。 应用程序生存期事件 • 独立应用程序(传统风格的 Windows 应用程序，这些应用程序作为要安装到客户端计算机并从客户端计算机运…...
【Git】任何位置查看git日志
需求 现需要查看指定项目中的某个文件的 Git 日志。如有 项目代码 jflowable ，需要查看其下文件 D:\z_workspace\jflowable\src\main\java\com\xzbd\jflowable\controller\TestController.java 的日志。 分析 一般的思路是，进入 jflowable 项目&#…...
Socket通讯使用的坑-消息合并发送-解决方法
关联文章 Socket通讯使用的坑-消息合并发送-CSDN博客 解决方法 /// <summary> /// 公共方法 /// </summary> public static class CommonMethods {/// <summary>/// 多个JSON对象字符串转成JSON字符串列表/// </summary>/// <param name"j…...
【Linux】基本指令
Hello everbody!这次咱们紧接着上一篇文章，继续介绍Linux操作系统的一些基本指令。这些指令是入门级别的，比较基础的。相当于windows中文件的复制，重命名，创建文件，创建目录之类的，还有如何在Linux中写c语言…...
JS中数组的相关方法介绍
push() 将一个或多个元素添加到数组的末尾，并返回新的长度。 let arr [1, 2, 3]; arr.push(4); // arr 现在是 [1, 2, 3, 4] pop() 删除并返回数组的最后一个元素 let arr [1, 2, 3, 4]; let last arr.pop(); // last 现在是 4，arr 现在是 [1, …...
mybtis动态SQL注解 脚本动态SQL\方法中构建SQL\SQL语句构造器
mybtis动态SQL注解 动态SQL注解脚本动态SQL方法中构建SQLSQL语句构造器 动态SQL注解 分类： 脚本动态SQL：XML配置方式的动态SQL，是用<script>的方式把它照搬过来，用注解来实现。适用于xml配置转换到注解配置方法中构建SQL&…...
TikTok电商加快闭环，独享IP为运营带来哪些好处?
近日有消息称TikTok电商在加快闭环，以后商家可能无法继续在TikTok上为其他电商平台或独立站引流了。如今“TikTok Shop Shopping Center”平台正在构建，将各种购物渠道整合为一体，这可能是一种趋势，意味着TikTok逐渐从社交应用转型…...
LaTeX系列4——列表
无序列表 \documentclass[UTF-8]{ctexart}\begin{document} \begin{itemize}\item{列表项1}\item{列表项2}\item{列表项3} \end{itemize} \end{document} 有序列表 \documentclass[UTF-8]{ctexart}\begin{document} \begin{enumerate}\item{列表项1}\item{列表项2}\item{列表…...
JNI笔记
JNI笔记 背景Demo代码JNI.javaMainActivity.javaAndroid.mkApplication.mkcom_stone_javacallc_JNI.hjavacallc.cbuild.gradle 背景 Demo代码 代码结构 JNI.java package com.stone.javacallc;/*** Created by stoneWang* Created on 2024/1/16* java调用C*/ public class …...
使用nginx的proxy_cache实现静态资源的缓存
nginx的版本 ./nginx -v nginx version: nginx/1.9.15需求 要求nginx缓存静态资源，如js、css、图片等，避免对静态资源的访问直接穿透到后端的j2ee应用侧，提高后端j2ee应用的运行效率。 配置方法 针对js、css、图片文件 分别增加缓存路径的…...
【Golang】Perl 正则表达式语法的支持示例
背景 在 Golang 中，标准库的正则表达式包 regexp 是基于 RE2 语法的，并不直接支持 Perl 正则表达式的全部功能。虽然 Golang 的标准库并不直接提供对 Perl 正则表达式的支持，但是您可以使用第三方库来实现与 Perl 兼容的正则表达式功能。 一…...
手写一个std::function
前言 在《std::function从实践到原理》中我们分析了std::function的实现原理，但这只是纸上谈兵。要想理解为什么这么实现，最好的办法还是想想要是自己手写一个要怎么实现。本文不想直接呈现最终版本，因为那样读者看不到某段代码是为了什么才…...
04--MySQL函数的使用
1、SQL函数的使用 当我们学习编程语言的时候，经常会遇到函数。函数的好处是，它可以把我们经常使用的代码封装起来，需要的时候直接调用即可。这样既提高了编写代码的效率，又提高了可维护性。在SQL中函数主要要对数据进行处理&…...
imgaug库指南（28）：从入门到精通的【图像增强】之旅（万字长文）
引言 在深度学习和计算机视觉的世界里，数据是模型训练的基石，其质量与数量直接影响着模型的性能。然而，获取大量高质量的标注数据往往需要耗费大量的时间和资源。正因如此，数据增强技术应运而生，成为了解决这一问题的…...
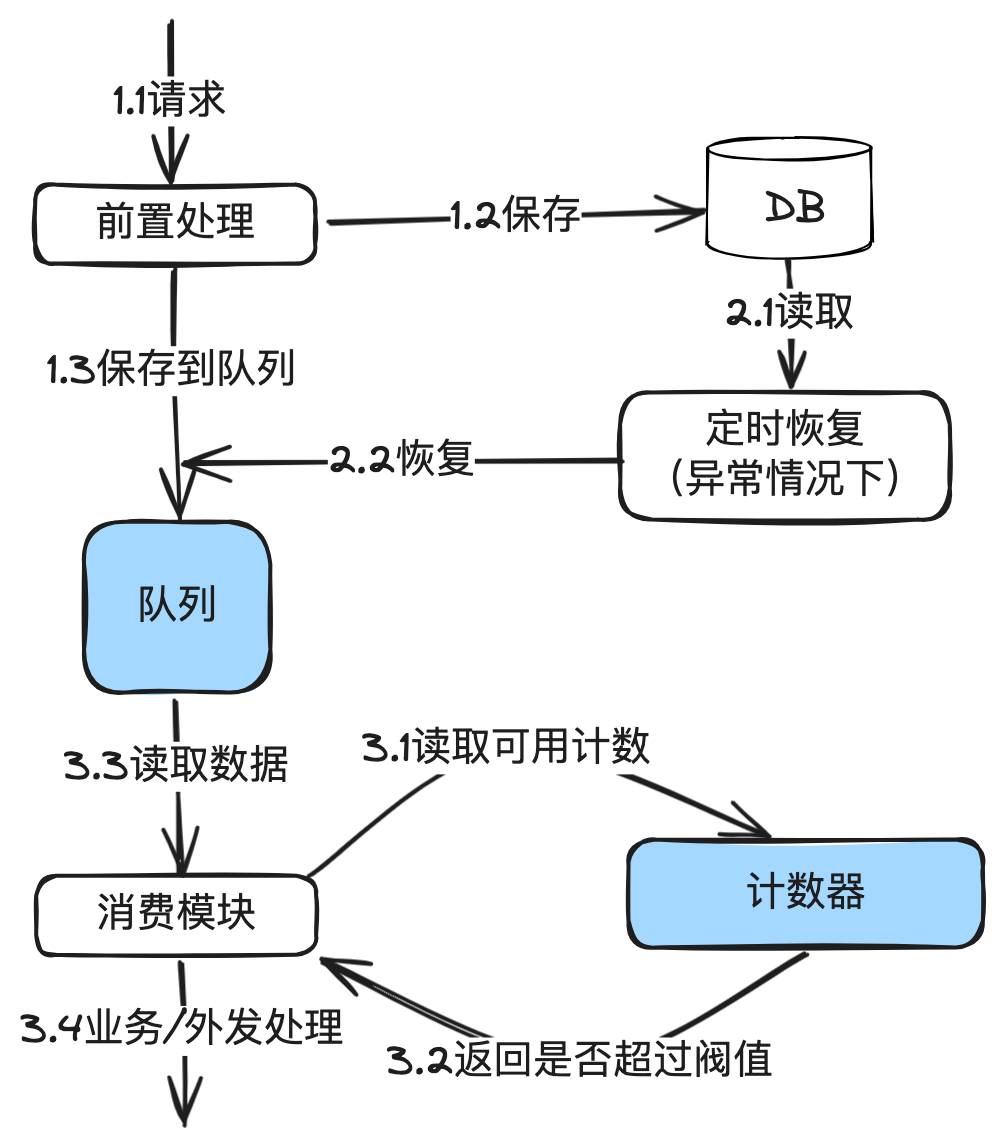
精确掌控并发：漏桶算法在分布式环境下并发流量控制的设计与实现
这是《百图解码支付系统设计与实现》专栏系列文章中的第（16）篇，也是流量控制系列的第（3）篇。点击上方关注，深入了解支付系统的方方面面。 本篇重点讲清楚漏桶原理，在支付系统的应用场景&#x…...
【Redis】Redis面试热点
Redis 集群有哪些方案？ 主从复制：解决了高并发问题 哨兵模式：解决了高并发，高可用问题 分片集群：解决了海量数据存储，高并发写的问题 主从复制 图示： 主从复制：单节点 Redis 并发…...
TDengine 快速体验（Docker 镜像方式）
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能，本节首先介绍如何通过 Docker 快速体验 TDengine，然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker，请使用 安装包的方式快…...
调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候，遇到了一些问题，记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中，选择 环境 -> 常规 ，将其中的颜色主题改成深色 点击确定，更改完成...
【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统，可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析：自动解析Markdown文档结构PPT模板分析：分析PPT模板的布局和风格智能布局决策：匹配内容与合适的PPT布局自动…...
Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面（Target 选项卡）1. IROM1（用于配置 Flash）2. IRAM1（用于配置 RAM）二、链接器设置界面（Linker 选项卡）1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数（如果没有勾选上面…...
微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
从零实现STL哈希容器：unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说，直接开始吧！ 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
零基础设计模式——行为型模式 - 责任链模式
第四部分：行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习！行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想：使多个对象都有机会处…...
C++使用 new 来创建动态数组
问题： 不能使用变量定义数组大小 原因： 这是因为数组在内存中是连续存储的，编译器需要在编译阶段就确定数组的大小，以便正确地分配内存空间。如果允许使用变量来定义数组的大小，那么编译器就无法在编译时确定数组的大…...
面向无人机海岸带生态系统监测的语义分割基准数据集
描述：海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而，目前该领域仍面临一个挑战，即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...