2024华数杯国际数学建模A题思路模型详解
2024华数杯国际数学建模A题思路论文:1.17上午第一时间持续更新,详细内容见文末名片
建立一个模型来描述放射性废水在海水中的扩散速率和方向,考虑到涉及的物理过程和环境因素的复杂性,我们通常会使用一个简化的扩散模型作为起点。在这种情况下,我们可以使用一个被广泛应用于环境工程和物理海洋学的模型:阿德韦克斯-扩散方程。这个方程考虑了物质由于流体运动(阿德韦克斯项)和由于浓度梯度引起的分子扩散(扩散项)的传输。
阿德韦克斯-扩散方程
阿德韦克斯-扩散方程的一维形式如下: ∂C∂t+u∂C∂x=D∂2C∂x2 \frac{\partial C}{\partial t} + u \frac{\partial C}{\partial x} = D \frac{\partial^2 C}{\partial x^2} 其中: - C(x,t)C(x, t) 是时间 tt 和位置 xx 处的污染物浓度。 - uu 是流体(在这种情况下是海水)的速度。 - DD 是扩散系数。
模型参数
- 初始条件:在 t=0t = 0 时,1095吨放射性废水被排放到一个特定的位置。这可以被建模为一个浓度峰值。
- 流体速度 uu:这需要来自海洋流动数据。
- 扩散系数 DD:这依赖于海水的物理性质和放射性物质的特性。
实施和预测
使用这个方程,我们可以通过数值方法(如有限差分法)来模拟污染物随时间的扩散。我们将设置初始条件和边界条件,然后模拟从2023年8月27日到9月27日的扩散过程。最终的模拟结果将给出在不同时间和位置的浓度分布,从而可以预测污染范围和程
在上述模型中,我们假设了一定的流体速度和扩散系数,并将放射性废水的初始释放量设为1095吨,集中在一个特定点上。根据模型的结果,我们可以看到从排放点开始,放射性废水的浓度随着距离的增加而逐渐减少。
考虑大气环流和日本的地理位置对放射性废水扩散的影响,我们需要将大气-海洋相互作用和区域海洋流动模式纳入考虑。
- 大气环流对海洋表面流动的影响:风力可以显著影响海洋表层的流动方向和速率,特别是在近海区域。
- 日本周边的海洋流动特征:北太平洋流动模式,如黑潮(Kuroshio Current)等强劲的海洋流,对污染物的扩散路径和速率有显著影响。
- 季节性变化:季节变化会影响海洋和大气的温度、风向和海流强度,进而影响扩散过程。
- 垂直混合和深层流动:海洋深层水体的流动对于长期和深层扩散也很重要。
建模方法
- 耦合大气-海洋模型:这类模型能够同时模拟大气和海洋之间的能量、质量和动量交换。这对于理解风力如何影响海面流动特别重要。
- 区域海洋流动模型:这些模型专注于特定区域(如北太平洋),考虑局部海流、温度和盐度分布等因素。对于日本附近的海域,模型需要特别考虑黑潮等主要海流的影响。
- 垂直混合模型:这些模型考虑海水垂直方向的混合和流动,对于理解污染物如何从表面层扩散到深海非常重要。
- 数值模拟方法:这通常包括有限差分法、有限元法或谱方法,用于求解复杂的流体动力学方程。
预测扩散速率和方向
在这种建模框架下,预测放射性废水的扩散速率和方向将涉及以下步骤:
- 初始条件设置:根据放射性废水的实际排放量和位置设置模型的初始条件。
- 运行模拟:利用上述模型和数值方法来模拟从排放开始到特定时间点的扩散过程。
- 结果分析:分析模拟结果,确定放射性废水在不同时间点的分布,从而预测其在日本周边海域的扩散速率和方向。
为了预测2023年9月27日日本附近海域的放射性废水污染范围和程度,我们可以使用前面提到的二维阿德韦克斯-扩散方程。我们使用一个简化的网格来演示基本的数值方法。
import numpy as np
import matplotlib.pyplot as plt# 参数设置
D_x = 0.1 # x方向的扩散系数
D_y = 0.1 # y方向的扩散系数
u = 0.05 # x方向的流速
v = 0.02 # y方向的流速Lx = 500 # x方向的长度(km)
Ly = 500 # y方向的长度(km)
dx = 5 # x方向的空间步长(km)
dy = 5 # y方向的空间步长(km)
dt = 0.1 # 时间步长(天)nx = int(Lx/dx) + 1 # x方向的网格点数
ny = int(Ly/dy) + 1 # y方向的网格点数
nt = int(30/dt) + 1 # 时间步数# 初始条件
C = np.zeros((nx, ny))
C[0, 0] = 1095 # 初始时刻在(0,0)处放置1095吨放射性废水# 二维阿德韦克斯-扩散方程的数值解
for t in range(1, nt):C[1:-1, 1:-1] = (C[1:-1, 1:-1] -u * dt / dx * (C[1:-1, 1:-1] - C[0:-2, 1:-1]) -v * dt / dy * (C[1:-1, 1:-1] - C[1:-1, 0:-2]) +D_x * dt / dx**2 * (C[2:, 1:-1]上面的图表展示了30天后(即2023年9月27日)放射性废水在海水中的预测扩散情况。在这个模拟中,我们使用了假设的流速和扩散系数,以及简化的二维网格。
在这个模型中,放射性废水从初始排放点(图中左下角)开始扩散。扩散是由水流的流动(由参数 u 和 v 控制)和分子扩散过程(由扩散系数 D_x 和 D_y 控制)共同作用的结果。图中的颜色深浅表示不同区域的放射性废水浓度。
问题二:
2023年,日本政府已三次倾倒放射性废水。如果未来不再进行倾倒,请建立一个数学模型来研究三次倾倒后放射性废水的扩散路径。考虑海洋环流模式、水动力、海底地形、水深变化、潮汐影响和季节波动等因素。预测污染中国领海所需的时间。请对这一问题进行数学建模
为了研究日本三次倾倒放射性废水后的扩散路径,并预测污染到达中国领海所需的时间,我们选择数学模型来描述放射性物质在海水中的运动。最常用的是多维阿德韦克斯-扩散方程,它可以表达物质在流体中因流动和扩散造成的运输过程。
2. 模型方程
在三维空间中,阿德韦克斯-扩散方程可以写为: ∂C∂t+u∂C∂x+v∂C∂y+w∂C∂z=Dx∂2C∂x2+Dy∂2C∂y2+Dz∂2C∂z2 \frac{\partial C}{\partial t} + u \frac{\partial C}{\partial x} + v \frac{\partial C}{\partial y} + w \frac{\partial C}{\partial z} = D_x \frac{\partial^2 C}{\partial x^2} + D_y \frac{\partial^2 C}{\partial y^2} + D_z \frac{\partial^2 C}{\partial z^2} 其中,C(x,y,z,t)C(x, y, z, t) 是放射性物质的浓度,u,v,wu, v, w 是流速分量,Dx,Dy,DzD_x, D_y, D_z 是相应方向的扩散系数。
为了更深入地理解放射性废水扩散模型,考虑一些额外的方程和数学概念。
1. 海洋流体动力学的基本方程
纳维-斯托克斯方程
用于描述流体运动的速度场,对于海水流动,该方程的一般形式是: ρ(∂u∂t+u⋅∇u)=−∇p+μ∇2u+ρg \rho \left( \frac{\partial \mathbf{u}}{\partial t} + \mathbf{u} \cdot \nabla \mathbf{u} \right) = -\nabla p + \mu \nabla^2 \mathbf{u} + \rho \mathbf{g} 其中,u\mathbf{u} 是流速向量,ρ\rho 是密度,pp 是压力,μ\mu 是动力粘度,g\mathbf{g} 是重力加速度。
连续性方程
描述质量守恒,对于不可压缩流体(如水),方程简化为: ∇⋅u=0 \nabla \cdot \mathbf{u} = 0
2. 扩散方程
考虑水体中放射性物质的扩散,使用扩散方程: ∂C∂t=D∇2C \frac{\partial C}{\partial t} = D \nabla^2 C 这里,CC 是放射性物质的浓度,DD 是扩散系数。
3. 潮汐和季节变化模型
潮汐模型
潮汐对海流的影响可以通过添加一个随时间变化的速度场来模拟,例如: utide(x,y,t)=Utide(x,y)cos(ωt+ϕ) \mathbf{u}_{tide}(x, y, t) = \mathbf{U}_{tide}(x, y) \cos(\omega t + \phi) 其中,Utide(x,y)\mathbf{U}_{tide}(x, y) 表示潮汐引起的最大流速分布,ω\omega 是潮汐频率,ϕ\phi 是相位常数。
季节性变化
季节性变化对海洋环流和温度的影响可以通过引入时间依赖的参数来模拟,例如海水温度 T(x,y,z,t)T(x, y, z, t) 和盐度 S(x,y,z,t)S(x, y, z, t) 的变化。
4. 综合模型
将上述方程综合起来,我们得到一个更完整的模型,用以描述放射性废水的扩散: ∂C∂t+u⋅∇C=D∇2C+Ssource \frac{\partial C}{\partial t} + \mathbf{u} \cdot \nabla C = D \nabla^2 C + S_{source} 其中,SsourceS_{source} 是源项,代表放射性废水的排放。
为了分析放射性废水倾倒事件对中国未来渔业经济的长期影响,我们可以使用统计方法来处理调查数据,并结合经济模型来预测可能的经济影响。首先,我们来分析调查数据。 1. 调查数据分析 根据提供的调查数据,我们可以计算出在放射性废水事件前后改变饮食习惯的人数比例。我们将使用卡方检验来确定改变。 卡方检验的结果显示,卡方统计量为 277.63,P 值为 2.46×10−622.46×10−62。这个极低的 P 值表明,放射性废水事件前后人们对于购买和食用海鲜的态度有显著的变化。 2. 经济影响预测 接下来,我们可以使用这些数据来预测对渔业经济的长期影响。 假设和简化 需求下降:假设不再食用海鲜的人群将不再购买海产品。 价格弹性:需求量的减少将导致价格下降,进而可能影响供给。 市场调整:长期来看,市场可能会逐渐适应新的需求水平。
要对放射性废水倾倒对中国未来渔业经济的长期影响进行数学建模,可以使用条件概率和基本的概率理论。首先,我们可以定义一些符号:
- P(E)P(E) 表示一个人在放射性废水倾倒前吃海鲜的概率。
- P(F)P(F) 表示一个人在放射性废水倾倒后吃海鲜的概率。
- P(E|F)P(E|F) 表示一个人在放射性废水倾倒后仍然吃海鲜的条件概率。
- P(F|E)P(F|E) 表示一个人在放射性废水倾倒前吃海鲜的条件概率。
我们可以使用这些概率来估计未来渔业经济的长期影响。首先,我们可以计算放射性废水倾倒前后吃海鲜的人数:
- 放射性废水倾倒前吃海鲜的人数:P(E)×10000P(E) \times 10000
- 放射性废水倾倒后吃海鲜的人数:P(F)×10000P(F) \times 10000
然后,我们可以计算放射性废水倾倒前后不吃海鲜的人数:
- 放射性废水倾倒前不吃海鲜的人数:10000−P(E)×1000010000 - P(E) \times 10000
- 放射性废水倾倒后不吃海鲜的人数:10000−P(F)×1000010000 - P(F) \times 10000
接下来,我们可以考虑吃海鲜和不吃海鲜的人对渔业经济的影响。假设吃海鲜的人平均每年在渔业上花费X1X_1元,不吃海鲜的人平均每年在渔业上花费X2X_2元。
放射性废水倾倒前吃海鲜的人对渔业经济的年度贡献:
P(E)×10000×X1P(E) \times 10000 \times X_1
放射性废水倾倒前不吃海鲜的人对渔业经济的年度贡献:
(1−P(E))×10000×X2(1 - P(E)) \times 10000 \times X_2
放射性废水倾倒后吃海鲜的人对渔业经济的年度贡献:
P(F)×10000×X1P(F) \times 10000 \times X_1
放射性废水倾倒后不吃海鲜的人对渔业经济的年度贡献:
(1−P(F))×10000×X2(1 - P(F)) \times 10000 \times X_2
最后,我们可以比较放射性废水倾倒前后的渔业经济总贡献,以评估长期影响。
以下是LaTeX数学公式,用于表示上述计算:
吃海鲜的人数: 放射性废水倾倒前:放射性废水倾倒前:P(E)×10000 \text{放射性废水倾倒前:} P(E) \times 10000 放射性废水倾倒后:放射性废水倾倒后:P(F)×10000 \text{放射性废水倾倒后:} P(F) \times 10000
不吃海鲜的人数: 放射性废水倾倒前:放射性废水倾倒前:10000−P(E)×10000 \text{放射性废水倾倒前:} 10000 - P(E) \times 10000 放射性废水倾倒后:放射性废水倾倒后:10000−P(F)×10000 \text{放射性废水倾倒后:} 10000 - P(F) \times 10000
渔业经济年度贡献: 放射性废水倾倒前吃海鲜的人:放射性废水倾倒前吃海鲜的人:P(E)×10000×X1 \text{放射性废水倾倒前吃海鲜的人:} P(E) \times 10000 \times X_1 放射性废水倾倒前不吃海鲜的人:放射性废水倾倒前不吃海鲜的人:(1−P(E))×10000×X2 \text{放射性废水倾倒前不吃海鲜的人:} (1 - P(E)) \times 10000 \times X_2 放射性废水倾倒后吃海鲜的人:放射性废水倾倒后吃海鲜的人:P(F)×10000×X1 \text{放射性废水倾倒后吃海鲜的人:} P(F) \times 10000 \times X_1 放射性废水倾倒后不吃海鲜的人:放射性废水倾倒后不吃海鲜的人:(1−P(F))×10000×X2 \text{放射性废水倾倒后不吃海鲜的人:} (1 - P(F)) \times 10000 \times X_2
使用数学建模来分析日本排放放射性废水30年后的情况,需要建立一个更加详细和复杂的模型,该模型将考虑放射性物质的传输、稀释、衰变以及海洋环境中的生物地球化学过程。这样的模型通常需要使用流体动力学和放射性物质传输的偏微分方程来描述。
- 放射性物质传输方程: ∂C∂t=D∇2C−λC+Q \frac{\partial C}{\partial t} = D \nabla^2 C - \lambda C + Q 其中,C(x,t)C(\mathbf{x}, t) 是放射性物质的浓度,DD 是扩散系数,λ\lambda 是衰变常数,Q(x,t)Q(\mathbf{x}, t) 是源项,表示放射性废水的排放。
- 海洋水流模型: ∂u∂t+(u⋅∇)u=−1ρ∇p+ν∇2u+g \frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u} \cdot \nabla) \mathbf{u} = -\frac{1}{\rho} \nabla p + \nu \nabla^2 \mathbf{u} + \mathbf{g} 其中,u(x,t)\mathbf{u}(\mathbf{x}, t) 是流速向量,p(x,t)p(\mathbf{x}, t) 是压力,ν\nu 是动粘性系数,g\mathbf{g} 是重力加速度。
- 放射性衰变: λ=ln2T1/2 \lambda = \frac{\ln 2}{T_{1/2}} 其中,T1/2T_{1/2} 是放射性物质的半衰期。
from fenics import *
from mshr import *# 创建一个矩形域,代表研究区域
domain = Rectangle(Point(0, 0), Point(100, 50))# 创建一个代表排放点的圆
radius = 1.0
circle = Circle(Point(20, 25), radius)# 从矩形域中减去圆,得到研究区域的几何形状
mesh = generate_mesh(domain - circle, 64)# 定义函数空间
V = FunctionSpace(mesh, 'P', 1)# 定义边界条件
def boundary(x, on_boundary):return on_boundarybc = DirichletBC(V, Constant(0), boundary)# 定义放射性衰变常数和扩散系数
lambda_ = Constant(0.1)
D = Constant(0.01)# 定义时间步长和总时间
dt = 0.1
T = 30 # 30 years# 定义放射性物质传输方程
C = Function(V)
C_n = interpolate(Constant(0), V)# 定义试验函数
v = TestFunction(V)# 定义时间循环
for t in range(int(T/dt)):# 更新源项Q = Expression('exp(-pow(x[0]-20, 2)/0.1 - pow(x[1]-25, 2)/0.1)', degree=2)# 求解方程F = (C - C_n)/dt*v*dx + D*dot(grad(C), grad(v))*dx - lambda_*C*v*dx - Q*v*dxsolve(F == 0, C, bc)# 更新前一个时间步的解C_n.assign(C)# 输出结果
file = File('radioactive_diffusion.pvd')
file << C相关文章:

2024华数杯国际数学建模A题思路模型详解
2024华数杯国际数学建模A题思路论文:1.17上午第一时间持续更新,详细内容见文末名片 建立一个模型来描述放射性废水在海水中的扩散速率和方向,考虑到涉及的物理过程和环境因素的复杂性,我们通常会使用一个简化的扩散模型作为起点…...

JS-定时器-间歇函数(一)
• 定时器函数介绍 定时器函数在开发中的使用场景 网页中经常会需要一种功能:每隔一段时间需要自动执行一段代码,不需要我们手动去触发例如:网页中的倒计时要实现这种需求,需要定时器函数定时器函数有两种,今天我先讲…...
AttributeError: module ‘openai‘ has no attribute ‘error‘解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...
每日一记:一个windows的bat脚本工具集
最近在工作上遇到要校验文件的问题,例如,下载了一个文件之后,通过查看文件的md5来校验文件是否完整,这个动作在linux上很简单,但在windows上也不难,可以通过 certutil 命令实现,该命令通常可用于…...
Apache Zeppelin学习记录2
Apache Zeppelin学习记录2 文章目录 Apache Zeppelin学习记录2前言一、基础调用二、带参数调用1.代码块要增加一行z.textbox("folder_path", "input")2.读取result 总结 前言 上一章讲了如何使用zeppelin来接入python,本节我们来看看如何使用R…...

[原创][R语言]股票分析实战[11]:读取股票数据文件的细节: 提取目标列数据
[简介] 常用网名: 猪头三 出生日期: 1981.XX.XX QQ联系: 643439947 个人网站: 80x86汇编小站 https://www.x86asm.org 编程生涯: 2001年~至今[共22年] 职业生涯: 20年 开发语言: C/C、80x86ASM、PHP、Perl、Objective-C、Object Pascal、C#、Python 开发工具: Visual Studio、D…...
【kafka】记录用-----------1
主题(topic):消息的第一次分类 根据人为的划分条件将消息分成不同的主题 主题的划分是人为的根据不同的任务情景去划分 比如,我们有两个主题,一个是"订单",另一个是"库存"。每个主题代…...

uniapp 实现tabBar-switchTab之间的传参
一、需求: tabbar之间跳转页面时,需要传递一个参数。 官方文档明确说明: 跳转tabBar栏的页面只能使用 uni.switchTab 并且url 路径后面不能传递参数。 二、解决方法: 方法1:setStorageSync(本地缓存) //index.vue 页 onclick …...
geemap学习笔记049:下载Landsat数据时遇到的一个问题
前言 最近在下载Landsat 8 地面反射率数据(Surface Reflectance)时,遇到了一个问题,无论是使用geemap.ee_export_image_to_drive() 函数还是geemap.download_ee_image() 函数下载的数据,易康都打不开,显示…...
基于pyqt5+scapy 根据ip 具体端口 进行扫描 的程序
先给出代码 import sysfrom PyQt5 import uic from PyQt5.QtWidgets import *from scapy.all import * import argparse import logging from scapy.layers.inet import IP, TCP from scapy.sendrecv import sr1class MyWindow(QWidget):def __init__(self):super().__init__(…...

Redis:原理速成+项目实战——Redis企业级项目实战终结篇(HyperLogLog实现UV统计)
👨🎓作者简介:一位大四、研0学生,正在努力准备大四暑假的实习 🌌上期文章:Redis:原理速成项目实战——Redis实战14(BitMap实现用户签到功能) 📚订阅专栏&am…...

Python的集合set用法介绍与例子
用法简介 Python的集合(set)是一种无序且不重复的元素序列。它类似于列表和元组,但集合中的元素是唯一的,没有重复的值。集合在Python中用于执行一些特定的操作,例如消除重复元素、检查元素是否存在等。 下面是一些关…...
服务器感染了.pings勒索病毒,如何确保数据文件完整恢复?
导言: 随着科技的不断进步,网络犯罪也在不断演变。其中之一的.pings勒索病毒是一种危险的恶意软件,它能够加密用户的数据文件,并要求支付赎金以解密这些文件。在本文中,91数据恢复将介绍.pings勒索病毒,以…...

go语言(二)----常量
1、单个常量用const进行定义。 const a int 100 2、多个常量用const()进行定义。 const ( a 10 b 20 ) 3、iota 与const()来表示枚举类型 const( a iota b c ) package mainimp…...

VSC ctrl+鼠标左键点击后,返回原来位置的方法
windows 在使用VSC编写代码时,我们常常用到Ctrl鼠标左键的方式来查看类或变量名的定义声明,看完之后我们想回到程序原来的位置,此时可以通过Alt ←(方向左键)来返回到原来的位置。...
还在为crontab表达式发愁吗,快使用这个工具
是不是每次要定义cron表达式的时候,都去百度翻找资料,cron表达式难写难记真是苦天下程序员久已。有没有什么不拥记的办法就轻松掌握呢?最近发现这个CrontabGuru神器,强烈推荐,真是广大程序员的福音了。 简介 Crontab…...

61. Spring事务传播行为实现原理
61. Spring事务传播行为实现原理 Spring的事务信息是存在ThreadLocal中的, 所以一个线程永远只能有一个事务 融入:当传播行为是融入外部事务则拿到ThreadLocal中的Connection、共享一个数据库连接共同提交、回滚;创建新事务:当传播行为是创建新事务,会将嵌套新事务存入Th…...
智能合约笔记
前言: 首先了解下为什么会出现智能合约,打个比方现在有两个人A和B打赌明天会不会下雨,每个人赌注100元,如果第二天下雨则A拿走200元,否则B拿走200元,这样就有一个问题,赌注要到第二天才能见效&…...
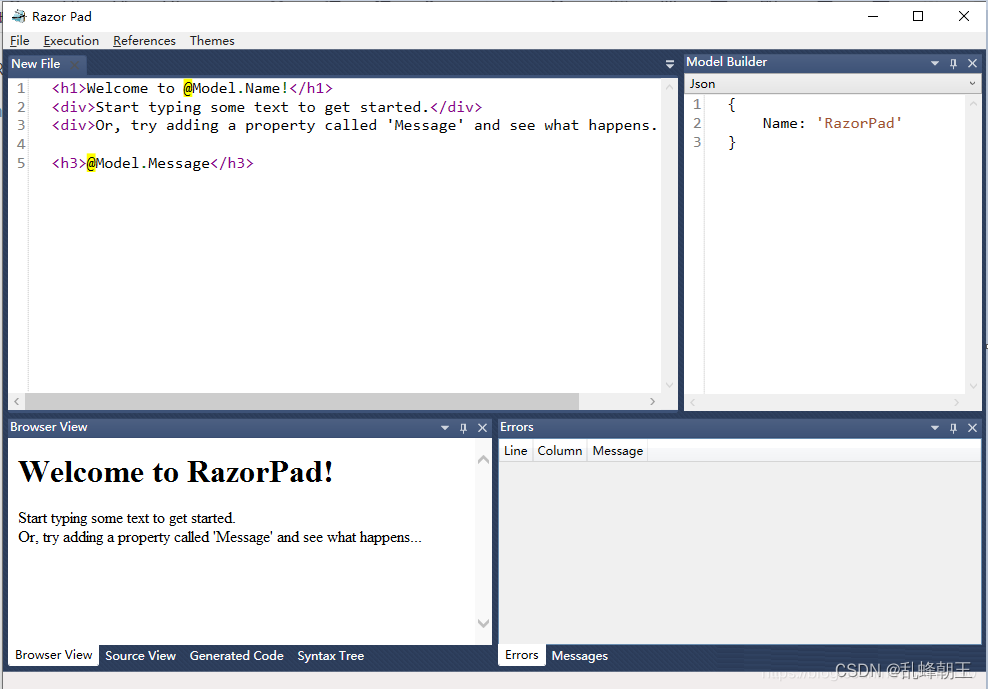
脱离于ASP.NET 和Visual Studio编辑Razor脚本
Razor Pad是一个编辑Razor脚本的工具,脱离于ASP.NET 和Visual Studio。 github地址:GitHub - RazorPad/RazorPad: RazorPad is a quick and simple stand-alone editing environment that allows anyone (even non-developers) to author Razor templat…...
MetaGPT前期准备与快速上手
大家好,MetaGPT 是基于大型语言模型(LLMs)的多智能体协作框架,GitHub star数量已经达到31.3k。 接下来我们聊一下快速上手 这里写目录标题 一、环境搭建1.python 环境2. MetaGpt 下载 二、MetaGPT配置1.调用 ChatGPT API 服务2.简…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
