2024年第二届“华数杯”国际大学生数学建模竞赛 (A题 MCM)| 废水扩散分析 |数学建模完整代码+建模过程全解全析
当大家面临着复杂的数学建模问题时,你是否曾经感到茫然无措?作为2022年美国大学生数学建模比赛的O奖得主,我为大家提供了一套优秀的解题思路,让你轻松应对各种难题。
让我们来看看华数杯的A题!

完整内容可以在文章末尾领取!
建立一个模型来描述放射性废水在海水中的扩散速率和方向,考虑到涉及的物理过程和环境因素的复杂性,我们通常会使用一个简化的扩散模型作为起点。在这种情况下,我们可以使用一个被广泛应用于环境工程和物理海洋学的模型:阿德韦克斯-扩散方程。这个方程考虑了物质由于流体运动(阿德韦克斯项)和由于浓度梯度引起的分子扩散(扩散项)的传输。
阿德韦克斯-扩散方程
阿德韦克斯-扩散方程的一维形式如下:
∂ C ∂ t + u ∂ C ∂ x = D ∂ 2 C ∂ x 2 \frac{\partial C}{\partial t} + u \frac{\partial C}{\partial x} = D \frac{\partial^2 C}{\partial x^2} ∂t∂C+u∂x∂C=D∂x2∂2C
其中:
- C ( x , t ) C(x, t) C(x,t) 是时间 t t t 和位置 x x x 处的污染物浓度。
- u u u 是流体(在这种情况下是海水)的速度。
- D D D 是扩散系数。
模型参数
-
初始条件:在 t = 0 t = 0 t=0 时,1095吨放射性废水被排放到一个特定的位置。这可以被建模为一个浓度峰值。
-
流体速度 u u u:这需要来自海洋流动数据。
-
扩散系数 D D D:这依赖于海水的物理性质和放射性物质的特性。
实施和预测
使用这个方程,我们可以通过数值方法(如有限差分法)来模拟污染物随时间的扩散。我们将设置初始条件和边界条件,然后模拟从2023年8月27日到9月27日的扩散过程。最终的模拟结果将给出在不同时间和位置的浓度分布,从而可以预测污染范围和程
在上述模型中,我们假设了一定的流体速度和扩散系数,并将放射性废水的初始释放量设为1095吨,集中在一个特定点上。根据模型的结果,我们可以看到从排放点开始,放射性废水的浓度随着距离的增加而逐渐减少。
考虑大气环流和日本的地理位置对放射性废水扩散的影响,我们需要将大气-海洋相互作用和区域海洋流动模式纳入考虑。
-
大气环流对海洋表面流动的影响:风力可以显著影响海洋表层的流动方向和速率,特别是在近海区域。
-
日本周边的海洋流动特征:北太平洋流动模式,如黑潮(Kuroshio Current)等强劲的海洋流,对污染物的扩散路径和速率有显著影响。
-
季节性变化:季节变化会影响海洋和大气的温度、风向和海流强度,进而影响扩散过程。
-
垂直混合和深层流动:海洋深层水体的流动对于长期和深层扩散也很重要。
建模方法
-
耦合大气-海洋模型:这类模型能够同时模拟大气和海洋之间的能量、质量和动量交换。这对于理解风力如何影响海面流动特别重要。
-
区域海洋流动模型:这些模型专注于特定区域(如北太平洋),考虑局部海流、温度和盐度分布等因素。对于日本附近的海域,模型需要特别考虑黑潮等主要海流的影响。
-
垂直混合模型:这些模型考虑海水垂直方向的混合和流动,对于理解污染物如何从表面层扩散到深海非常重要。
-
数值模拟方法:这通常包括有限差分法、有限元法或谱方法,用于求解复杂的流体动力学方程。
预测扩散速率和方向
在这种建模框架下,预测放射性废水的扩散速率和方向将涉及以下步骤:
- 初始条件设置:根据放射性废水的实际排放量和位置设置模型的初始条件。
- 运行模拟:利用上述模型和数值方法来模拟从排放开始到特定时间点的扩散过程。
- 结果分析:分析模拟结果,确定放射性废水在不同时间点的分布,从而预测其在日本周边海域的扩散速率和方向。
为了预测2023年9月27日日本附近海域的放射性废水污染范围和程度,我们可以使用前面提到的二维阿德韦克斯-扩散方程。我们使用一个简化的网格来演示基本的数值方法。
import numpy as np
import matplotlib.pyplot as plt# 参数设置
D_x = 0.1 # x方向的扩散系数
D_y = 0.1 # y方向的扩散系数
u = 0.05 # x方向的流速
v = 0.02 # y方向的流速Lx = 500 # x方向的长度(km)
Ly = 500 # y方向的长度(km)
dx = 5 # x方向的空间步长(km)
dy = 5 # y方向的空间步长(km)
dt = 0.1 # 时间步长(天)nx = int(Lx/dx) + 1 # x方向的网格点数
ny = int(Ly/dy) + 1 # y方向的网格点数
nt = int(30/dt) + 1 # 时间步数# 初始条件
C = np.zeros((nx, ny))
C[0, 0] = 1095 # 初始时刻在(0,0)处放置1095吨放射性废水# 二维阿德韦克斯-扩散方程的数值解
for t in range(1, nt):C[1:-1, 1:-1] = (C[1:-1, 1:-1] -u * dt / dx * (C[1:-1, 1:-1] - C[0:-2, 1:-1]) -v * dt / dy * (C[1:-1, 1:-1] - C[1:-1, 0:-2]) +D_x * dt / dx**2 * (C[2:, 1:-1]

上面的图表展示了30天后(即2023年9月27日)放射性废水在海水中的预测扩散情况。在这个模拟中,我们使用了假设的流速和扩散系数,以及简化的二维网格。
在这个模型中,放射性废水从初始排放点(图中左下角)开始扩散。扩散是由水流的流动(由参数 u 和 v 控制)和分子扩散过程(由扩散系数 D_x 和 D_y 控制)共同作用的结果。图中的颜色深浅表示不同区域的放射性废水浓度。
问题二:
2023年,日本已三次倾倒放射性废水。如果未来不再进行倾倒,请建立一个数学模型来研究三次倾倒后放射性废水的扩散路径。考虑海洋环流模式、水动力、海底地形、水深变化、潮汐影响和季节波动等因素。预测污染中国领海所需的时间。请对这一问题进行数学建模
为了研究日本三次倾倒放射性废水后的扩散路径,并预测污染到达中国领海所需的时间,我们选择数学模型来描述放射性物质在海水中的运动。最常用的是多维阿德韦克斯-扩散方程,它可以表达物质在流体中因流动和扩散造成的运输过程。
2. 模型方程
在三维空间中,阿德韦克斯-扩散方程可以写为:
∂ C ∂ t + u ∂ C ∂ x + v ∂ C ∂ y + w ∂ C ∂ z = D x ∂ 2 C ∂ x 2 + D y ∂ 2 C ∂ y 2 + D z ∂ 2 C ∂ z 2 \frac{\partial C}{\partial t} + u \frac{\partial C}{\partial x} + v \frac{\partial C}{\partial y} + w \frac{\partial C}{\partial z} = D_x \frac{\partial^2 C}{\partial x^2} + D_y \frac{\partial^2 C}{\partial y^2} + D_z \frac{\partial^2 C}{\partial z^2} ∂t∂C+u∂x∂C+v∂y∂C+w∂z∂C=Dx∂x2∂2C+Dy∂y2∂2C+Dz∂z2∂2C
其中, C ( x , y , z , t ) C(x, y, z, t) C(x,y,z,t) 是放射性物质的浓度, u , v , w u, v, w u,v,w 是流速分量, D x , D y , D z D_x, D_y, D_z Dx,Dy,Dz 是相应方向的扩散系数。
为了更深入地理解放射性废水扩散模型,考虑一些额外的方程和数学概念。
1. 海洋流体动力学的基本方程
纳维-斯托克斯方程
用于描述流体运动的速度场,对于海水流动,该方程的一般形式是:
ρ ( ∂ u ∂ t + u ⋅ ∇ u ) = − ∇ p + μ ∇ 2 u + ρ g \rho \left( \frac{\partial \mathbf{u}}{\partial t} + \mathbf{u} \cdot \nabla \mathbf{u} \right) = -\nabla p + \mu \nabla^2 \mathbf{u} + \rho \mathbf{g} ρ(∂t∂u+u⋅∇u)=−∇p+μ∇2u+ρg
其中, u \mathbf{u} u 是流速向量, ρ \rho ρ 是密度, p p p 是压力, μ \mu μ 是动力粘度, g \mathbf{g} g 是重力加速度。
连续性方程
描述质量守恒,对于不可压缩流体(如水),方程简化为:
∇ ⋅ u = 0 \nabla \cdot \mathbf{u} = 0 ∇⋅u=0
2. 扩散方程
考虑水体中放射性物质的扩散,使用扩散方程:
∂ C ∂ t = D ∇ 2 C \frac{\partial C}{\partial t} = D \nabla^2 C ∂t∂C=D∇2C
这里, C C C 是放射性物质的浓度, D D D 是扩散系数。
3. 潮汐和季节变化模型
潮汐模型
潮汐对海流的影响可以通过添加一个随时间变化的速度场来模拟,例如:
u t i d e ( x , y , t ) = U t i d e ( x , y ) cos ( ω t + ϕ ) \mathbf{u}_{tide}(x, y, t) = \mathbf{U}_{tide}(x, y) \cos(\omega t + \phi) utide(x,y,t)=Utide(x,y)cos(ωt+ϕ)
其中, U t i d e ( x , y ) \mathbf{U}_{tide}(x, y) Utide(x,y) 表示潮汐引起的最大流速分布, ω \omega ω 是潮汐频率, ϕ \phi ϕ 是相位常数。
季节性变化
季节性变化对海洋环流和温度的影响可以通过引入时间依赖的参数来模拟,例如海水温度 T ( x , y , z , t ) T(x, y, z, t) T(x,y,z,t) 和盐度 S ( x , y , z , t ) S(x, y, z, t) S(x,y,z,t) 的变化。
4. 综合模型
将上述方程综合起来,我们得到一个更完整的模型,用以描述放射性废水的扩散:
∂ C ∂ t + u ⋅ ∇ C = D ∇ 2 C + S s o u r c e \frac{\partial C}{\partial t} + \mathbf{u} \cdot \nabla C = D \nabla^2 C + S_{source} ∂t∂C+u⋅∇C=D∇2C+Ssource
其中, S s o u r c e S_{source} Ssource 是源项,代表放射性废水的排放。
import numpy as np
import matplotlib.pyplot as plt# Parameters
L = 2000 # Total distance in km (e.g., from Japan to China's coast)
dx = 10 # Spatial step in km
D = 0.1 # Diffusion coefficient
u = 5 # Flow velocity in km/day (assumed constant for simplicity)# Simulation parameters
nx = int(L/dx) + 1 # Number of spatial points
C = np.zeros(nx) # Initial concentration
C[0] = 1 # Representing the initial waste dump# Time parameters
dt = 0.1 # Time step in days
total_time = 365 # Total simulation time in days
nt = int(total_time/dt) + 1# Advection-diffusion simulation
for t in range(nt):Cn = C.copy()for i in range(1, nx-1):C[i] = Cn[i] - u * dt / dx * (Cn[i] - Cn[i-1]) + D * dt / dx**2 * (Cn[i+1] - 2*Cn[i] + Cn[i-1])# Checking if the concentration at the far end (China's coast) is above a thresholdif C[-1] > 0.001: # Threshold concentrationprint(f"Pollution reached China's coast after {t * dt} days.")break# Visualizing the result
plt.plot(np.linspace(0, L, nx), C)
plt.xlabel('Distance from source (km)')
plt.ylabel('Concentration')
plt.title('Radioactive Pollution Spread Over Time')
plt.show()
代码将逐步模拟放射性废水在海洋中的扩散过程,并在污染物浓度在中国领海达到一个设定阈值时报告所需时间。

为了分析放射性废水倾倒事件对中国未来渔业经济的长期影响,我们可以使用统计方法来处理调查数据,并结合经济模型来预测可能的经济影响。首先,我们来分析调查数据。
- 调查数据分析
根据提供的调查数据,我们可以计算出在放射性废水事件前后改变饮食习惯的人数比例。我们将使用卡方检验来确定改变。
卡方检验的结果显示,卡方统计量为 277.63,P 值为 2.46×10−622.46×10−62。这个极低的 P 值表明,放射性废水事件前后人们对于购买和食用海鲜的态度有显著的变化。 - 经济影响预测
接下来,我们可以使用这些数据来预测对渔业经济的长期影响。
假设和简化
需求下降:假设不再食用海鲜的人群将不再购买海产品。
价格弹性:需求量的减少将导致价格下降,进而可能影响供给。
市场调整:长期来看,市场可能会逐渐适应新的需求水平。
要对放射性废水倾倒对中国未来渔业经济的长期影响进行数学建模,可以使用条件概率和基本的概率理论。首先,我们可以定义一些符号:
- P ( E ) P(E) P(E) 表示一个人在放射性废水倾倒前吃海鲜的概率。
- P ( F ) P(F) P(F) 表示一个人在放射性废水倾倒后吃海鲜的概率。
- P ( E ∣ F ) P(E|F) P(E∣F) 表示一个人在放射性废水倾倒后仍然吃海鲜的条件概率。
- P ( F ∣ E ) P(F|E) P(F∣E) 表示一个人在放射性废水倾倒前吃海鲜的条件概率。
我们可以使用这些概率来估计未来渔业经济的长期影响。首先,我们可以计算放射性废水倾倒前后吃海鲜的人数:
- 放射性废水倾倒前吃海鲜的人数: P ( E ) × 10000 P(E) \times 10000 P(E)×10000
- 放射性废水倾倒后吃海鲜的人数: P ( F ) × 10000 P(F) \times 10000 P(F)×10000
然后,我们可以计算放射性废水倾倒前后不吃海鲜的人数:
- 放射性废水倾倒前不吃海鲜的人数: 10000 − P ( E ) × 10000 10000 - P(E) \times 10000 10000−P(E)×10000
- 放射性废水倾倒后不吃海鲜的人数: 10000 − P ( F ) × 10000 10000 - P(F) \times 10000 10000−P(F)×10000
接下来,我们可以考虑吃海鲜和不吃海鲜的人对渔业经济的影响。假设吃海鲜的人平均每年在渔业上花费 X 1 X_1 X1元,不吃海鲜的人平均每年在渔业上花费 X 2 X_2 X2元。
放射性废水倾倒前吃海鲜的人对渔业经济的年度贡献:
P ( E ) × 10000 × X 1 P(E) \times 10000 \times X_1 P(E)×10000×X1
放射性废水倾倒前不吃海鲜的人对渔业经济的年度贡献:
( 1 − P ( E ) ) × 10000 × X 2 (1 - P(E)) \times 10000 \times X_2 (1−P(E))×10000×X2
放射性废水倾倒后吃海鲜的人对渔业经济的年度贡献:
P ( F ) × 10000 × X 1 P(F) \times 10000 \times X_1 P(F)×10000×X1
放射性废水倾倒后不吃海鲜的人对渔业经济的年度贡献:
( 1 − P ( F ) ) × 10000 × X 2 (1 - P(F)) \times 10000 \times X_2 (1−P(F))×10000×X2
最后,我们可以比较放射性废水倾倒前后的渔业经济总贡献,以评估长期影响。
以下是LaTeX数学公式,用于表示上述计算:
吃海鲜的人数:
放射性废水倾倒前: P ( E ) × 10000 \text{放射性废水倾倒前:} P(E) \times 10000 放射性废水倾倒前:P(E)×10000
放射性废水倾倒后: P ( F ) × 10000 \text{放射性废水倾倒后:} P(F) \times 10000 放射性废水倾倒后:P(F)×10000
不吃海鲜的人数:
放射性废水倾倒前: 10000 − P ( E ) × 10000 \text{放射性废水倾倒前:} 10000 - P(E) \times 10000 放射性废水倾倒前:10000−P(E)×10000
放射性废水倾倒后: 10000 − P ( F ) × 10000 \text{放射性废水倾倒后:} 10000 - P(F) \times 10000 放射性废水倾倒后:10000−P(F)×10000
渔业经济年度贡献:
放射性废水倾倒前吃海鲜的人: P ( E ) × 10000 × X 1 \text{放射性废水倾倒前吃海鲜的人:} P(E) \times 10000 \times X_1 放射性废水倾倒前吃海鲜的人:P(E)×10000×X1
放射性废水倾倒前不吃海鲜的人: ( 1 − P ( E ) ) × 10000 × X 2 \text{放射性废水倾倒前不吃海鲜的人:} (1 - P(E)) \times 10000 \times X_2 放射性废水倾倒前不吃海鲜的人:(1−P(E))×10000×X2
放射性废水倾倒后吃海鲜的人: P ( F ) × 10000 × X 1 \text{放射性废水倾倒后吃海鲜的人:} P(F) \times 10000 \times X_1 放射性废水倾倒后吃海鲜的人:P(F)×10000×X1
放射性废水倾倒后不吃海鲜的人: ( 1 − P ( F ) ) × 10000 × X 2 \text{放射性废水倾倒后不吃海鲜的人:} (1 - P(F)) \times 10000 \times X_2 放射性废水倾倒后不吃海鲜的人:(1−P(F))×10000×X2
使用数学建模来分析日本排放放射性废水30年后的情况,需要建立一个更加详细和复杂的模型,该模型将考虑放射性物质的传输、稀释、衰变以及海洋环境中的生物地球化学过程。这样的模型通常需要使用流体动力学和放射性物质传输的偏微分方程来描述。
- 放射性物质传输方程:
∂ C ∂ t = D ∇ 2 C − λ C + Q \frac{\partial C}{\partial t} = D \nabla^2 C - \lambda C + Q ∂t∂C=D∇2C−λC+Q
其中, C ( x , t ) C(\mathbf{x}, t) C(x,t) 是放射性物质的浓度, D D D 是扩散系数, λ \lambda λ 是衰变常数, Q ( x , t ) Q(\mathbf{x}, t) Q(x,t) 是源项,表示放射性废水的排放。 - 海洋水流模型:
∂ u ∂ t + ( u ⋅ ∇ ) u = − 1 ρ ∇ p + ν ∇ 2 u + g \frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u} \cdot \nabla) \mathbf{u} = -\frac{1}{\rho} \nabla p + \nu \nabla^2 \mathbf{u} + \mathbf{g} ∂t∂u+(u⋅∇)u=−ρ1∇p+ν∇2u+g
其中, u ( x , t ) \mathbf{u}(\mathbf{x}, t) u(x,t) 是流速向量, p ( x , t ) p(\mathbf{x}, t) p(x,t) 是压力, ν \nu ν 是动粘性系数, g \mathbf{g} g 是重力加速度。 - 放射性衰变:
λ = ln 2 T 1 / 2 \lambda = \frac{\ln 2}{T_{1/2}} λ=T1/2ln2
其中, T 1 / 2 T_{1/2} T1/2 是放射性物质的半衰期。
from fenics import *
from mshr import *# 创建一个矩形域,代表研究区域
domain = Rectangle(Point(0, 0), Point(100, 50))# 创建一个代表排放点的圆
radius = 1.0
circle = Circle(Point(20, 25), radius)# 从矩形域中减去圆,得到研究区域的几何形状
mesh = generate_mesh(domain - circle, 64)# 定义函数空间
V = FunctionSpace(mesh, 'P', 1)# 定义边界条件
def boundary(x, on_boundary):return on_boundarybc = DirichletBC(V, Constant(0), boundary)# 定义放射性衰变常数和扩散系数
lambda_ = Constant(0.1)
D = Constant(0.01)# 定义时间步长和总时间
dt = 0.1
T = 30 # 30 years# 定义放射性物质传输方程
C = Function(V)
C_n = interpolate(Constant(0), V)# 定义试验函数
v = TestFunction(V)# 定义时间循环
for t in range(int(T/dt)):# 更新源项Q = Expression('exp(-pow(x[0]-20, 2)/0.1 - pow(x[1]-25, 2)/0.1)', degree=2)# 求解方程F = (C - C_n)/dt*v*dx + D*dot(grad(C), grad(v))*dx - lambda_*C*v*dx - Q*v*dxsolve(F == 0, C, bc)# 更新前一个时间步的解C_n.assign(C)# 输出结果
file = File('radioactive_diffusion.pvd')
file << C
问题五
基于你的研究,写一封给联合国环境规划署的建议信,长度为1页。
[您的姓名] [您的地址] [城市,州,邮编] [电子邮件地址] [电话号码] [日期] 联合国环境规划署(UNEP) [收件人姓名]
[收件人职称] [地址] [城市,州,邮编] 尊敬的[收件人姓名],
我希望这封信能在您身体健康、精神愉悦的情况下收到。我写信是想表达我对日本最近决定开始将经过处理的福岛第一核电站放射性废水排放到太平洋的深切关切。作为一名[插入您的职业或专长]专家,我一直密切关注与此问题相关的进展及其对海洋生态系统和人类健康的潜在影响。我强烈相信,联合国环境规划署(UNEP)应介入并提供指导,以确保我们共同海洋的保护。
决定将大约125万吨含有氚和其他放射性同位素的经过处理的废水排放到太平洋,引发了重大的环境、健康和社会关切。尽管日本表示,废水将被处理和稀释,以满足国际标准,但对于这些行动对海洋生物、海产品安全和沿海社区福祉的长期影响,仍存在相当大的不确定性。
鉴于这一问题的潜在跨界性质,UNEP在处理这一局势方面发挥积极作用至关重要。我建议UNEP成立一个独立的科学小组,对福岛第一核电站排放处理废水的潜在环境与健康风险进行全面评估。这个小组应由来自海洋生物学、放射性生态学、海洋学、公共卫生等领域的专家组成。
此外,UNEP还应敦促日本在科学小组完成评估并提供关于如何最小化潜在风险的推荐之前,推迟废水的排放。在做出如此重大的决策时,基于最佳可用科学证据,并考虑所有利益相关者,包括当地社区、渔业和环保组织的关切和观点,至关重要。
除了科学评估外,UNEP还应促进受影响国家及利益相关者之间的国际对话,以确保透明度、信息共享和协作决策。这种对话应旨在解决与海洋生态系统潜在污染、海产品安全和沿海社区社会经济影响相关的问题。通过促进国际合作和相互理解,UNEP可以帮助缓解冲突,推动这一复杂问题的和平解决方案。
最后,我敦促UNEP提倡开发和实施严格的监测计划,以追踪太平洋中放射性污染物的扩散,并评估其对海洋生物和人类健康的潜在影响。这些计划应旨在确保我们海洋的长期可持续性,以及沿海人口的良好福祉。
感谢您关注这一紧急问题。我相信UNEP将采取果断行动,保护我们共同的海洋,促进现在和未来世代的福祉。 此致, [您的姓名]
更多内容具体可以看看我的下方名片!里面包含有认证杯一手资料与分析!
另外在赛中,我们也会陪大家一起解析认证杯的一些方向
关注 CS数模 团队,数模不迷路~
相关文章:

2024年第二届“华数杯”国际大学生数学建模竞赛 (A题 MCM)| 废水扩散分析 |数学建模完整代码+建模过程全解全析
当大家面临着复杂的数学建模问题时,你是否曾经感到茫然无措?作为2022年美国大学生数学建模比赛的O奖得主,我为大家提供了一套优秀的解题思路,让你轻松应对各种难题。 让我们来看看华数杯的A题! 完整内容可以在文章末…...

深度学习基础知识整理
自动编码器 Auto-encoders是一种人工神经网络,用于学习未标记数据的有效编码。它由两个部分组成:编码器和解码器。编码器将输入数据转换为一种更紧凑的表示形式,而解码器则将该表示形式转换回原始数据。这种方法可以用于降维,去噪,特征提取和生成模型。 自编码器的训练过…...

go语言GMP模式介绍以及协程案例展示
一. MPG模式 Go语言的调度模型被称为GMP,这是一个高效且复杂的调度系统,用于在可用的物理线程上调度goroutines(Go的轻量级线程)。GMP模型由三个主要组件构成:Goroutine、M(机器)和P࿰…...
码牛课堂首推——鸿蒙南北双向开发学习路线图标准版~
鸿蒙!鸿蒙!鸿蒙! 要说2023-2024年IT圈最火爆的名词,一定是鸿蒙! 2023年9月25日,华为发布会正式宣布2024年第一季度将推出HarmonyOS NEXT版本,这意味着鸿蒙原生应用开发将彻底摆脱Android手机系…...
(亲测可行)关于提高IDEA运行速度的方案
1.作者IDEA软件版本和计算机内存 Ultimate 2022.1.2版IDEA,计算机内存为12GB 2.修改配置以提高IDEA运行速度的误区-调高堆内存 很多文章会教调配置的内存,但大多是让你调高堆内存,比如会让你调高-Xms -Xmx ,这两种对应的是最…...

框架基础-Maven+SpringBoot入门
框架基础 Maven基础 Maven概述 Maven是为Java项目提供项目构建和依赖管理的工具 Maven三大功能 - 项目构建构建:是一个将代码从开发阶段到生产阶段的一个过程:清理,编译,测试,打包,安装,部署…...
uniapp微信小程序投票系统实战 (SpringBoot2+vue3.2+element plus ) -投票帖子排行实现
锋哥原创的uniapp微信小程序投票系统实战: uniapp微信小程序投票系统实战课程 (SpringBoot2vue3.2element plus ) ( 火爆连载更新中... )_哔哩哔哩_bilibiliuniapp微信小程序投票系统实战课程 (SpringBoot2vue3.2element plus ) ( 火爆连载更新中... )共计21条视频…...

用julia演示蝴蝶效应:洛伦兹吸引子
文章目录 Lorentz吸引子julia绘图关闭抗锯齿 蝴蝶效应的名字来源于蝴蝶扇动翅膀的动作,虽然这个动作微小,但可能会在数周后引起飓风等极端天气的发生。这种现象表明,微小的变化可能会被放大并产生非线性的结果。这个概念最早由美国气象学家爱…...

从车联网到智慧城市:智慧交通的革新之路
一、引言 1、智慧城市的概念和发展背景 智慧城市(Smart City)是指以信息技术为基础,运用信息与通信等手段,对城市各个核心系统各项关键数据进行感测、分析、整合和利用,实现对城市生活环境的感知、资源的调控&#x…...

模拟IIC通信
模拟IIC通信 IIC 模拟IIC通信底层接口时间控制(通信速度)功能实现对外接口EEPROM相关 底层接口 device是可以用来增加多个IIC设备管理的 void I2C_SET_SCL(unsigned char device, unsigned char bit_value) {bit_value ? MCU_SCL_H() : MCU_SCL_L(); }void I2C_SET_SDA(uns…...
安卓手机变iOS!
Launcher iOS 16 - 安卓手机秒变iOS Launcher iOS 16 是一款iOS启动器,可以将安卓手机桌面变成iOS样子,还有iOS的开机动画和景深效果! 下载链接:【Launcher iOS 16】 ...
Spring使用注解管理Bean
引入lib包 Spring对Bean管理的常用注解 Component组件(作用在类上) Spring中提供了Component的三个衍生注解:(功能在目前为止是一致的) Controller WEB层 Service 业务层 Repository 持久层 属性注入的注解:(使用注解注入的方式,可以不用提供set方法) Value 用于注入普…...
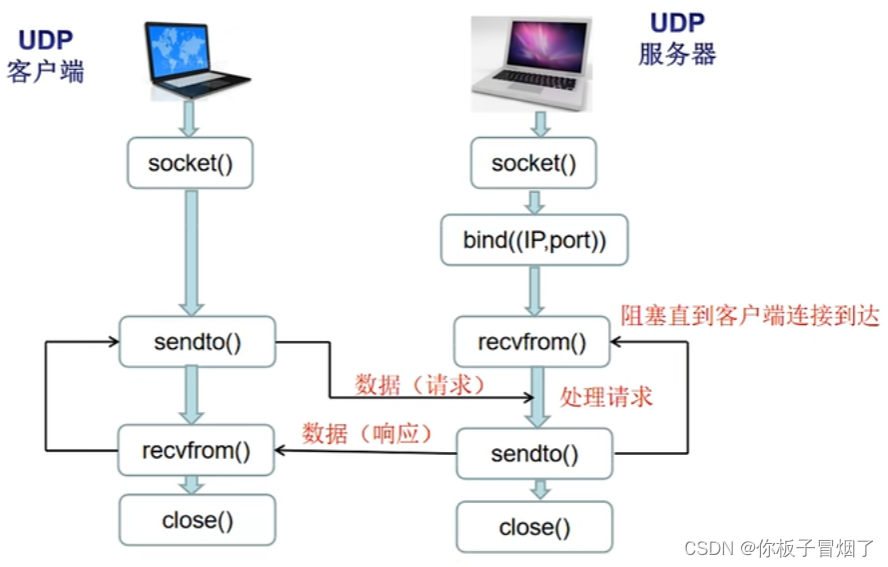
弟12章 网络编程
文章目录 网络协议概述 p164TCP协议与UDP协议的区别 p165TCP服务器端代码的编写 p166TCP服务器端流程 TCP客户端代码的编写 p167TCP客户端流程主机和客户端的通信流程 tcp多次通信服务器端代码 p168TCP多次通信客户端代码 p169UDP的一次双向通信 p170udp通信模型udp接收方代码u…...
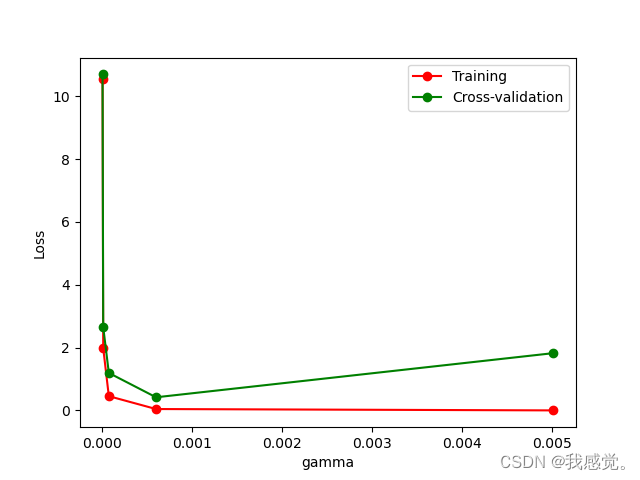
【sklearn练习】模型评估
一、交叉验证 cross_val_score 的使用 1、不用交叉验证的情况: from __future__ import print_function from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn.neighbors import KNeighborsClassifieriris…...
Gazebo的模型下载。
git clone zouxu634866/gazebo_modelshttps://gitee.com/zouxu6348660/gazebo_models.git,并完成路径配置。 (本文提供了gitee下载,国外的Github下载较慢。)...
支持方法重载吗?)
MyBatis - DAO 接口(Mapper.xml)支持方法重载吗?
方法重载(Method Overloading)是指在同一个类中定义多个方法,它们具有相同的方法名但参数列表不同。 Dao 在 MyBatis 的 DAO 层接口中,是允许方法重载的。 在 DAO 层接口中,可以根据不同的需求和条件定义多个方法&am…...
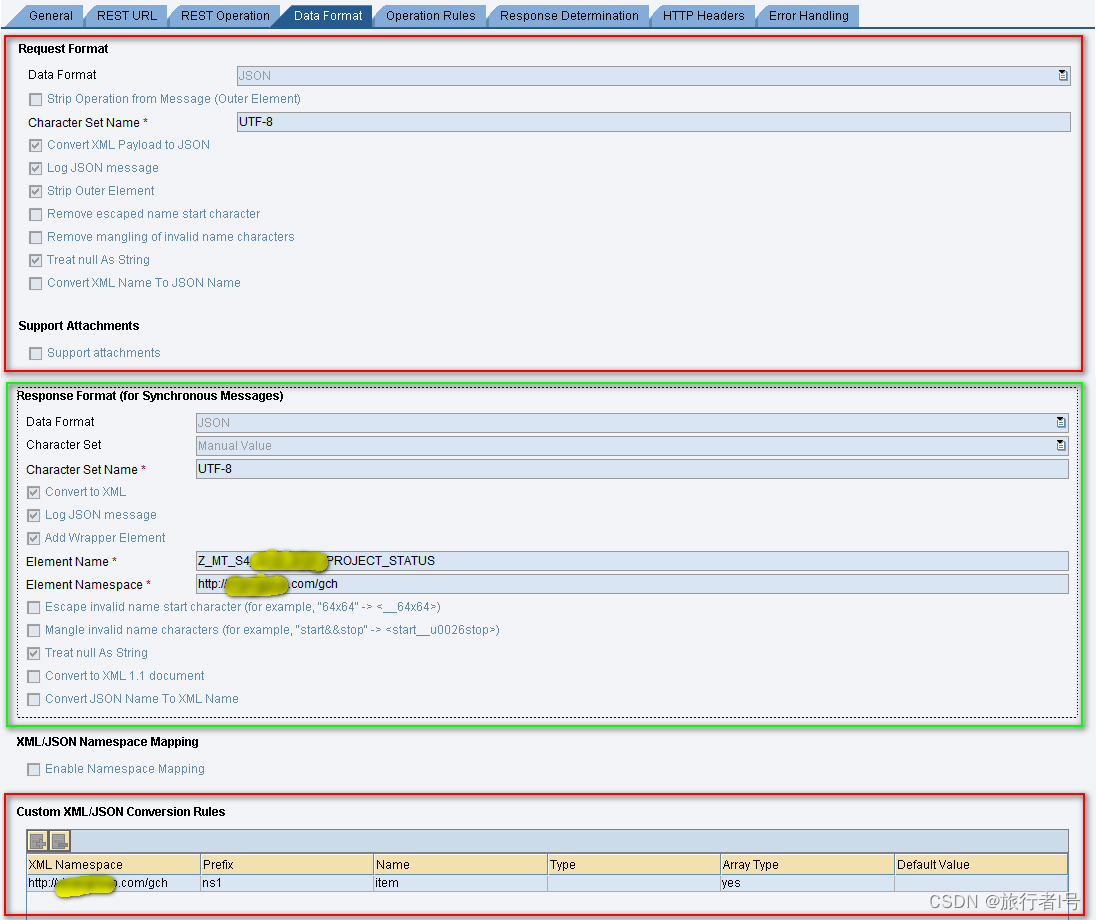
SAP PI之Rest adapter
一,简介 REST风格接口是以http为传输协议,以xml或json或text为有效负载。下图展示了REST到XI再返回的一个过程,一个REST接口包含的信息有:服务URL、URL中带的参数、http方法(post/get/put等)、http头部、body部分的有效载荷。而X…...
推荐几个Github高星GoLang管理系统
在Web开发领域,Go语言(Golang)以其高效、简洁、高并发等特性逐渐成为许多开发者的首选语言。有许多优秀的Go语言Web后台管理系统,这些项目星星众多,提供了丰富的功能和良好的代码质量。本文将介绍一些GitHub高星的GoLa…...

生成式对抗网络GAN
Generative Adversarial Nets由伊恩古德费洛(Ian J.Goodfellow)等人于2014年发表在Conference on Neural Information Processing Systems (NeurIPS)上。NeurIPS是机器学习和计算神经科学领域的顶级国际学术会议之一。 1. GAN在哪些领域大放异彩 图像生…...
Python如何使用Excel文件
使用Python操作Office——EXCEL 首先介绍下office win32 com接口,这个是MS为自动化提供的操作接口,比如我们打开一个EXCEL文档,就可以在里面编辑VB脚本,实现我们自己的效果。对于这种一本万利的买卖,Python怎么能放过…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...
