决战排序之巅(二)
决战排序之巅(二)
- 排序测试函数 void verify(int* arr, int n)
- 归并排序
- 递归方案
- 代码可行性测试
- 非递归方案
- 代码可行性测试
- 特点分析
- 计数排序
- 代码实现
- 代码可行性测试
- 特点分析
- 归并排序 VS 计数排序(Release版本)
- 说明
- 1w rand( ) 数据测试
- 10w rand( ) 数据测试
- 100w rand( ) 数据测试
- 1000w rand( ) 数据测试
- 测试代码
- 结语
欢迎来到决战排序之巅栏目,
本期给大家带来的是归并排序与计数排序的实现与比较。
在上期决战排序之巅(一)中,给大家带来了插入排序(希尔) 与 选择排序(堆排) 的实现与比较,感兴趣的可以看看。

排序测试函数 void verify(int* arr, int n)
主要功能:测试arr数组中的顺序是否全为非升序的顺序。
代码如下:
void verify(int* arr, int n)
{for (int i = 1; i < n; i++){assert(arr[i] >= arr[i - 1]);}
}
如果arr数组中顺序不全为非升序,则assert()直接终止程序;
若全为非升序,则程序可通过该函数。
归并排序
基本思想:采用分治算法,将已有的有序子序列进行合并,得到完全有序的序列;即先使每个子序列有序,再使子序列所合并的序列有序。
归并排序的核心步骤就是:分解与合并。
递归方案
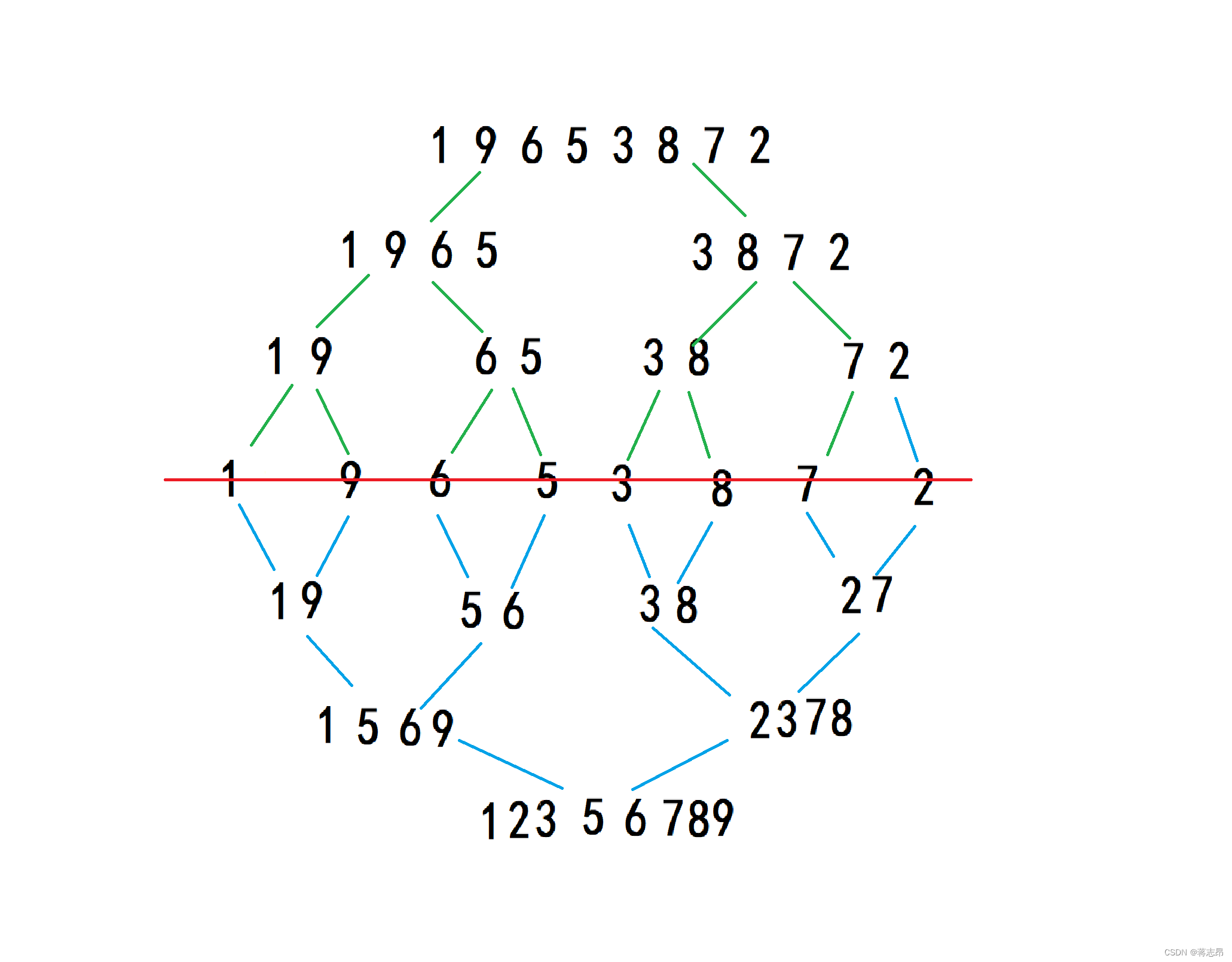
如下图所示:我们可以先将一组数据由大到小逐个分开,再依次合并。
下图绿线为分解,蓝线为合并。我们可以看到,排序数据分解时,当子序列内个数为1 时,不再分解;随后进行依次的合并,"1" "9" 合并为"1 9"的子序列,"5" "6"合并成"5 6"的体序列,同理可得"3 8" "2 7",再让子序列合并,"1 9 6 5"合并成"1 5 6 9"。"3 8"和"2 7"合并成"2 3 7 8"。最后两个字序列合并成"1 2 3 5 6 7 8 9"
至此,归并排序完毕。
具体代码,如下:
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);assert(tmp);_MergeSort(a, 0, n - 1, tmp);free(tmp);
}
void MergeSort(int* a, int n)是我们排序的调用函数,因为他的参数形式不宜用递归实现,所以我们可以写一个子函数void _MergeSort(int* a,int begin,int end ,int* tmp)来实现主要程序的编写,如下:
void _MergeSort(int* a,int begin,int end ,int* tmp)
{if (begin >= end)return;int mid = (begin + end) / 2;_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid+1, end, tmp);int left1 = begin, right1 = mid;int left2 = mid + 1, right2 = end;int i = 0;while (left1 <= right1 && left2 <= right2){if (a[left1] > a[left2])tmp[i++] = a[left2++];elsetmp[i++] = a[left1++];}while (left1 <= right1){tmp[i++] = a[left1++];}while (left2 <= right2){tmp[i++] = a[left2++];}memcpy(a + begin, tmp, i * sizeof(int));
}
我们先通过以下代码进行归并排序“分解”的实现
if (begin >= end)return; int mid = (begin + end) / 2;_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid+1, end, tmp);当子序列内个数为
1时,return 返回;当子序列内个数大于1时,进行以下编写:
有递归可知,此时的小标区间为[begin , mid] 与 [mid + 1 , end]是排好序的子区间,所有此时我们只要将其合并好就可以了。int left1 = begin, right1 = mid;int left2 = mid + 1, right2 = end;int i = 0;while (left1 <= right1 && left2 <= right2){if (a[left1] > a[left2])tmp[i++] = a[left2++];elsetmp[i++] = a[left1++];}while (left1 <= right1){tmp[i++] = a[left1++];}while (left2 <= right2){tmp[i++] = a[left2++];}memcpy(a + begin, tmp, i * sizeof(int));最后将tmp上的数据拷贝到a的[begin , end]区间即可。
代码可行性测试
void _test()
{int n = 100000000;int* arr = (int*)malloc(sizeof(int) * n);for (int i = 0; i < n; i++){arr[i] = rand();}MergeSort(arr, n);verify(arr, n);free(arr);
}
运行结果如下 :
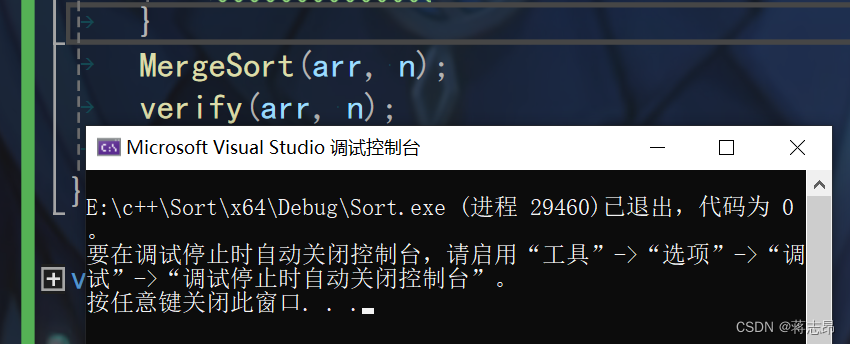
程序通过verify(int* arr int n)函数,且成功运行,代码无误。
非递归方案
在非递归方案中我们可以利用循环来实现,主要实现过程如下视频所示:
归并排序思想
我们可以定义一个gap并且gap的初始置为1,用来表示子序列的最小个数为1,随后在整体排完相邻两个子序列后,gap乘以2,此时数组内小标区间为 [ n ∗ g a p , n ∗ ( g a p ∗ 2 − 1 ) ] ∪ [ 0 , g a p − 1 ] , n ∈ N + [n * gap , n * (gap * 2-1)]\cup[0 , gap-1] ,n\in N^+ [n∗gap,n∗(gap∗2−1)]∪[0,gap−1],n∈N+是有序的,如此循环直到, n ≤ g a p n\leq gap n≤gap时跳出循环,代码如下:
void MergeSortNonR(int* a,int n)
{int* tmp = (int*)malloc(sizeof(int) * n);assert(tmp);int gap = 1;while (n > gap){for (int i = 0; i < n; i += gap * 2){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + gap * 2 - 1;int j = begin1;if (end1 >= n && begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy( a + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}free(tmp);
}
我们先看如何分解,利用gap来确定子序列的元数个数,再利用for循环来实现两个相邻子序列的排序(即下标区间[begin1,end1] , [begin2,end2]的排序)
注意:在分配完区间[begin1,end1] ,和[begin2,end2]后,我们要对区间范围的有效性进行检查,因为非递归的方案通过比较相邻的子序列,gap以2的幂次方所增长,适用的数组长度也为2的幂次方,所以我们要对end1 , begin2 , end2进行检查,如果end1 , begin2大于数组总个数n时,直接break即可,因为此时的[begin1,n-1]已经是有序的了;如果end2大于n则,令end2=n-1,此时我们只要排好[begin1,end2] , [begin2,n-1]即可,具体过程如下:for (int i = 0; i < n; i += gap * 2){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + gap * 2 - 1;int j = begin1;if (end1 >= n && begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}//合并过程}合并过程与递归方案相同,但需要注意的是数组拷贝的时候,
for循环依次拷贝一次。
代码可行性测试
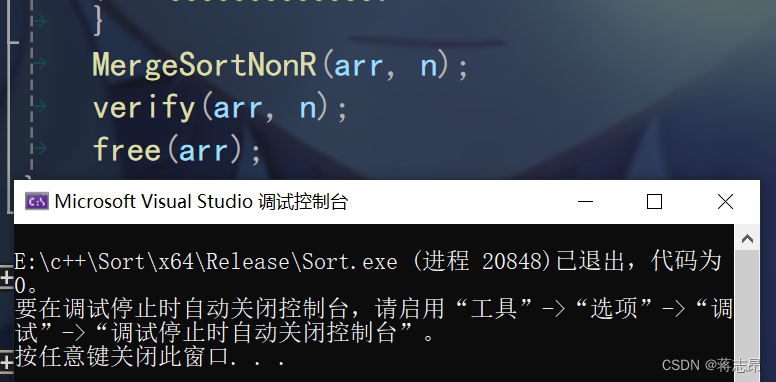
程序通过verify(int* arr int n)函数,且成功运行,代码无误。
特点分析
特性:归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
时间复杂度:O(N*logN)
空间复杂度:O(N)
稳定性:稳定
计数排序
基本思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。
代码实现
实现步骤:
- 选出要排序数组
a中的最值,再相减求出数组的相对范围 n = m a x − m i n + 1 n = max - min + 1 n=max−min+1 - 用calloc开辟
n个空间为tmp - 利用
i遍历a,让数组tmp[ a [ i ] − m i n a[i] - min a[i]−min]++ - 最后,再遍历
tmp, 此时tmp的数组下标 + min就表示数据的大小,tmp[数组下标]表示该数据的个数,所以在此时为a直接赋值即可。
具体代码如下:
void CountSort(int* a, int n)
{int max = a[0], min = a[0];int i = 0;for (i = 0; i < n; i++){if (max < a[i]){max = a[i];}if (min > a[i]){min = a[i];}}int* tmp = (int*)calloc((max - min + 1), sizeof(int));assert(tmp);for (i = 0; i < n; i++){tmp[a[i] - min]++;}int j = 0;for (i = 0; i < max - min + 1; i++){int count = tmp[i];while (count--){a[j++] = i + min;}}free(tmp);
}
代码可行性测试
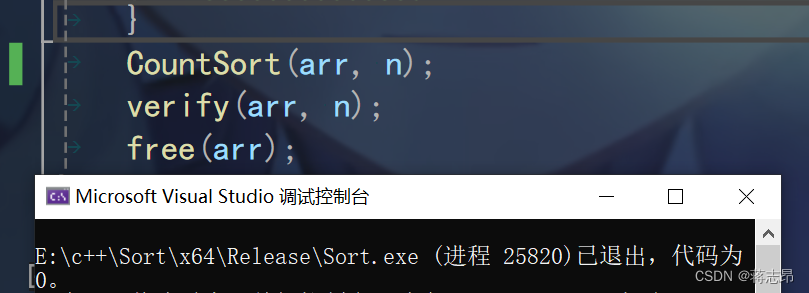
程序通过verify(int* arr int n)函数,且成功运行,代码无误。
特点分析
特点分析:计数排序在数据范围集中时,效率很高,但是适用范围及场景有限(例如:小数,结构体,字符串无法比较)
时间复杂度:O(MAX(N,范围))
空间复杂度:O(范围)
归并排序 VS 计数排序(Release版本)
说明
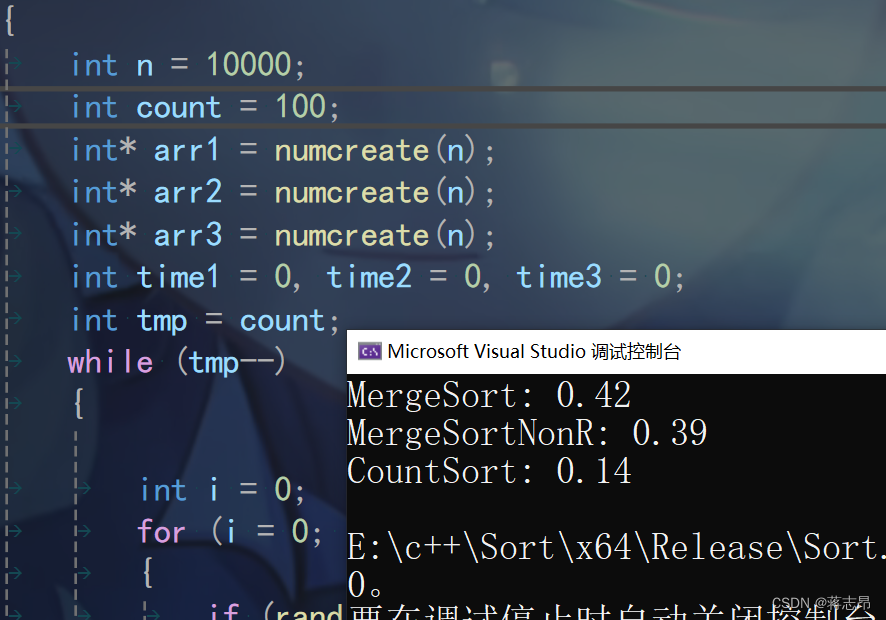
以下会分别对1w,10w,100w,1000w的数据进行100次的排序比较,并计算出排一趟的平均值。
下面是用来生成随机数的代码,可以确保正数与负数的随机分布。
for (i = 0; i < n; i++){if (rand() % 2){arr3[i] = arr2[i] = arr1[i] = -rand() + i;}else{arr3[i] = arr2[i] = arr1[i] = rand() - i;}}
介绍就到这里了,让我们来看看这100次排序中,谁才是你心目中的排序呢?
PS:100次只是一个小小的测试数据,有兴趣的朋友可以在自己电脑上测试更多的来比较哦。
1w rand( ) 数据测试
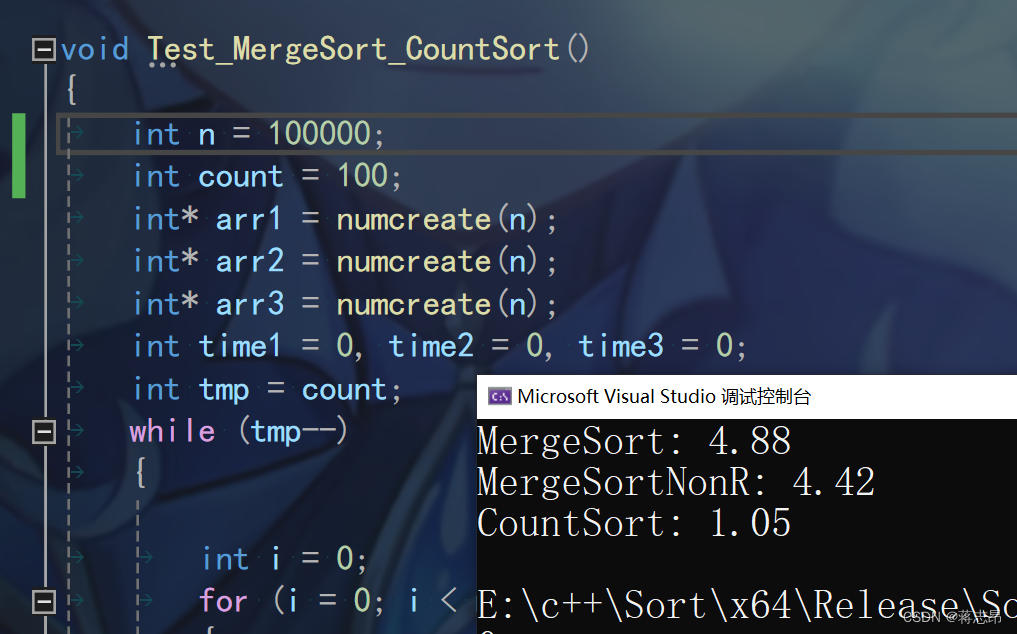
10w rand( ) 数据测试
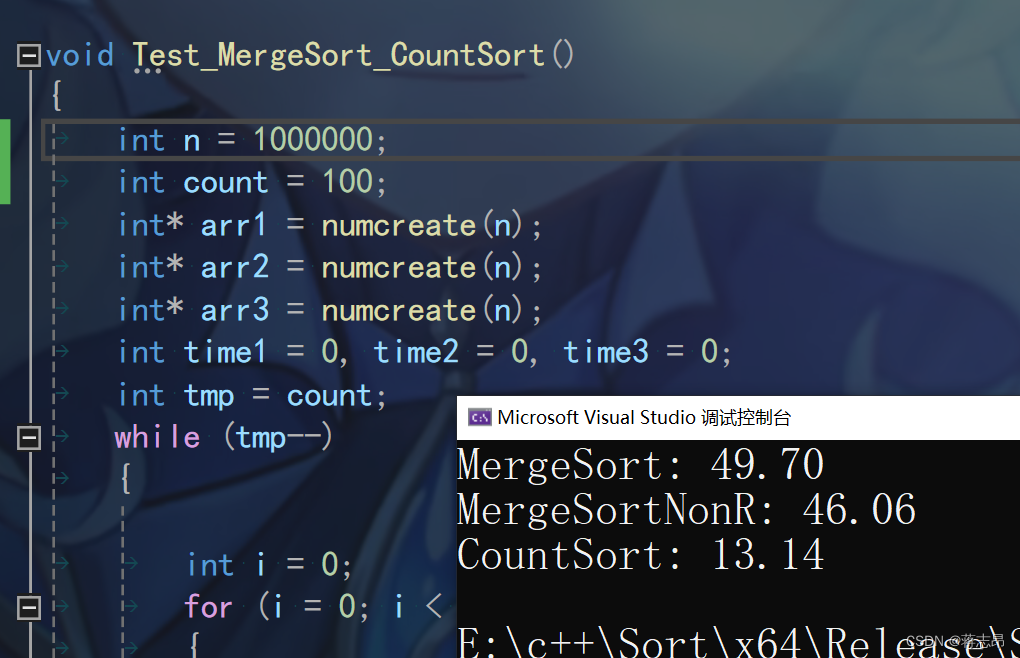
100w rand( ) 数据测试
1000w rand( ) 数据测试

测试代码
void Test_MergeSort_CountSort()
{int n = 10000000;int count = 100;int* arr1 = numcreate(n);int* arr2 = numcreate(n);int* arr3 = numcreate(n);int time1 = 0, time2 = 0, time3 = 0;int tmp = count;while (tmp--){int i = 0;for (i = 0; i < n; i++){if (rand() % 2){arr3[i] = arr2[i] = arr1[i] = -rand() + i;}else{arr3[i] = arr2[i] = arr1[i] = rand() - i;}}int begin1 = clock();MergeSort(arr1, n);int end1 = clock();int begin2 = clock();MergeSortNonR(arr2, n);int end2 = clock();int begin3 = clock();CountSort(arr3, n);int end3 = clock();time1 += end1 - begin1;time2 += end2 - begin2;time3 += end3 - begin3;}printf("MergeSort: %.2f\n", (float)time1/count);printf("MergeSortNonR: %.2f\n", (float)time2 / count);printf("CountSort: %.2f\n", (float)time3 / count);free(arr1);free(arr2);free(arr3);
}
从结果来看,计数排序快于归并排序,但它的局限性无法比较小数,结构体与字符串;
再看归并排序,非递归类的要略胜一筹哦。
结语
看完之后,谁才是你心目中的排序呢?
欢迎留言,让我们一起来期待在下一期 《决战排序之巅(三)》。
以上就是本期的全部内容喜欢请多多关注吧!!!
相关文章:

决战排序之巅(二)
决战排序之巅(二) 排序测试函数 void verify(int* arr, int n) 归并排序递归方案代码可行性测试 非递归方案代码可行性测试 特点分析 计数排序代码实现代码可行性测试 特点分析 归并排序 VS 计数排序(Release版本)说明1w rand( ) …...

自动化网络监控:每分钟自动检测网站可用性
🧙♂️ 诸位好,吾乃诸葛妙计,编程界之翘楚,代码之大师。算法如流水,逻辑如棋局。 📜 吾之笔记,内含诸般技术之秘诀。吾欲以此笔记,传授编程之道,助汝解技术难题。 &…...
Asp .Net Core 系列:集成 Ocelot+Consul实现网关、服务注册、服务发现
什么是Ocelot? Ocelot是一个开源的ASP.NET Core微服务网关,它提供了API网关所需的所有功能,如路由、认证、限流、监控等。 Ocelot是一个简单、灵活且功能强大的API网关,它可以与现有的服务集成,并帮助您保护、监控和扩展您的微…...

MSSQL行转列、列转行
行转列 SELECT * FROM student PIVOT ( SUM(score) FOR subject IN (语文, 数学, 英语) ) AS PivotedData; 列转行 SELECT * FROM student1 UNPIVOT ( score FOR subject IN ("语文","数学","英语") )AS PivotedData;...

【MySQL】创建和管理表
文章目录 前置 标识符命名规则一、MySQL数据类型二、创建和管理数据库2.1 创建数据库2.2 使用数据库2.3 修改数据库2.4 删除数据库 三、创建表3.1 创建方式一3.2 创建方式二3.3 查看数据表结构 四、修改表4.1 增加一个列4.2 修改一个列4.3 重命名一个列4.4 删除一个列 五、重命…...
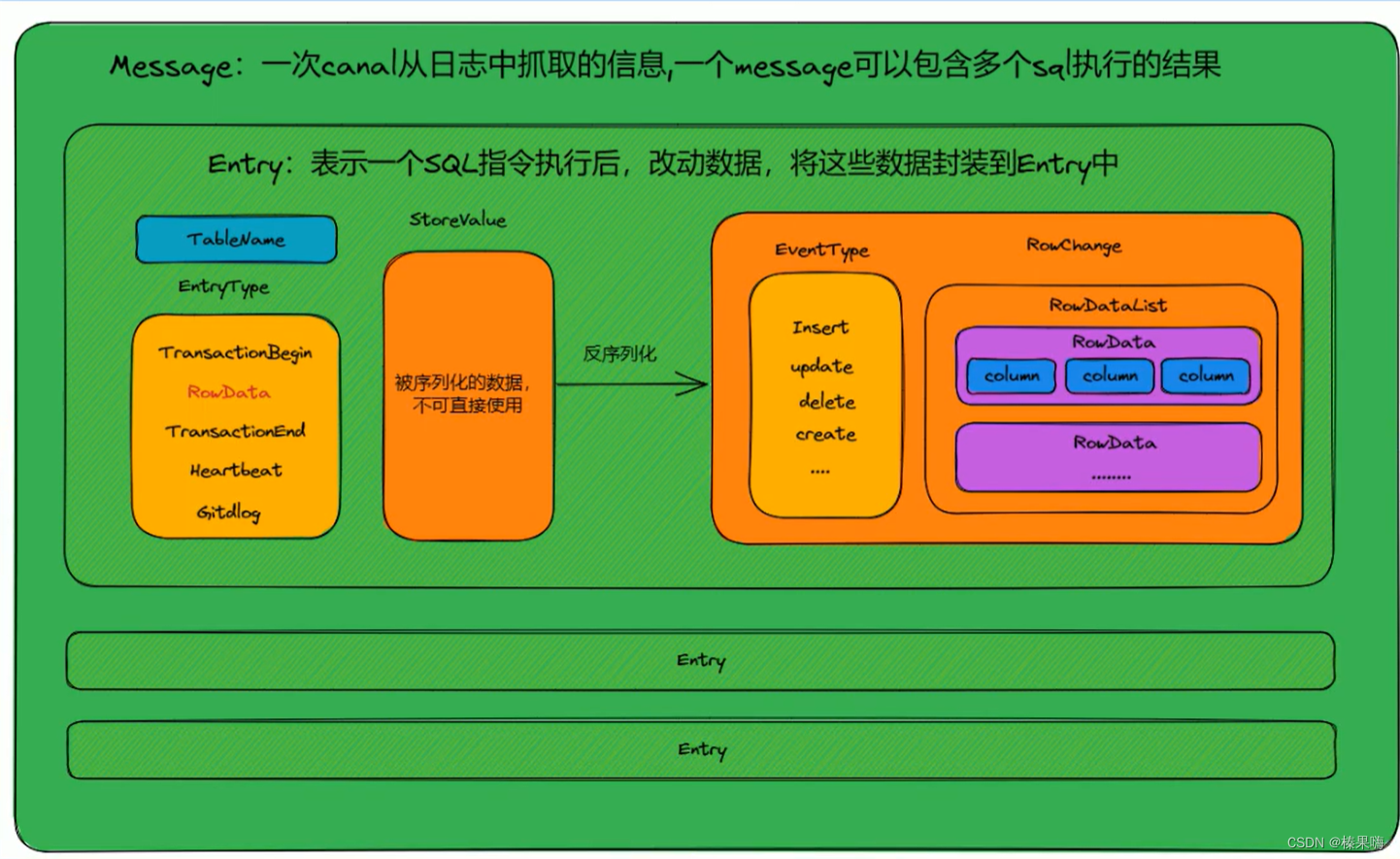
缓存和数据库一致性
前言: 项目的难点是如何保证缓存和数据库的一致性。无论我们是先更新数据库,后更新缓存还是先更新数据库,然后删除缓存,在并发场景之下,仍然会存在数据不一致的情况(也存在删除失败的情况,删除…...
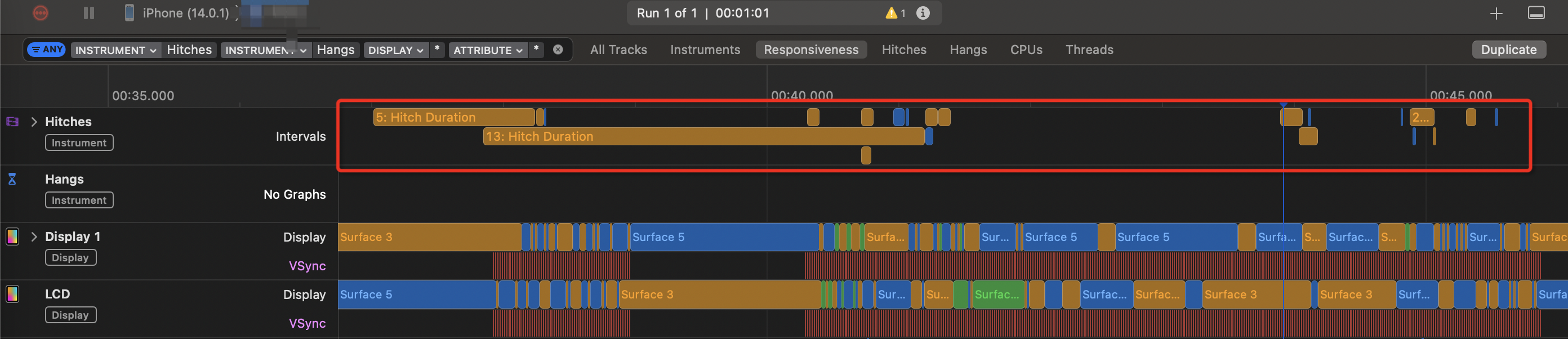
iOS UI掉帧和卡顿优化解决方案记录
UI卡顿原理 在 VSync 信号到来后,系统图形服务会通过 CADisplayLink 等机制通知 App,App 主线程开始在 CPU 中计算显示内容,比如视图的创建、布局计算、图片解码、文本绘制等。随后 CPU 会将计算好的内容提交到 GPU 去,由 GPU 进行…...
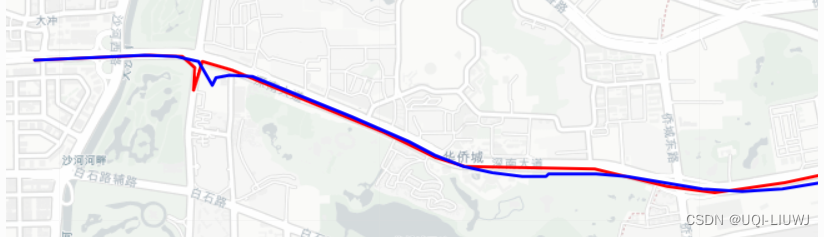
transbigdata 笔记: 轨迹密集化/稀疏化 轨迹平滑
1 密集化 transbigdata.traj_densify(data, col[Vehicleid, Time, Lng, Lat], timegap15) 轨迹致密化,保证至多每隔timegap秒都有一个轨迹点 这边插补使用的是pandas的interpolate,method设置的是index 1.1 举例 transbigdata 笔记: 官方…...

反向代理的本质是什么?
反向代理是一种网络架构模式,通常用于提供静态内容、处理安全、负载均衡和缓存等任务。在这种架构中,客户端发送的请求首先到达反向代理服务器,然后由反向代理服务器将请求转发给后端的实际服务器。反向代理服务器可以处理和修改请求和响应&a…...

Kali Linux保姆级教程|零基础从入门到精通,看完这一篇就够了!(附工具包)
作为一名从事网络安全的技术人员,不懂Kali Linux的话,连脚本小子都算不上。 Kali Linux预装了数百种享誉盛名的渗透工具,使你可以更轻松地测试、破解以及进行与数字取证相关的任何其他工作。 今天给大家分享一套Kali Linux资料合集…...
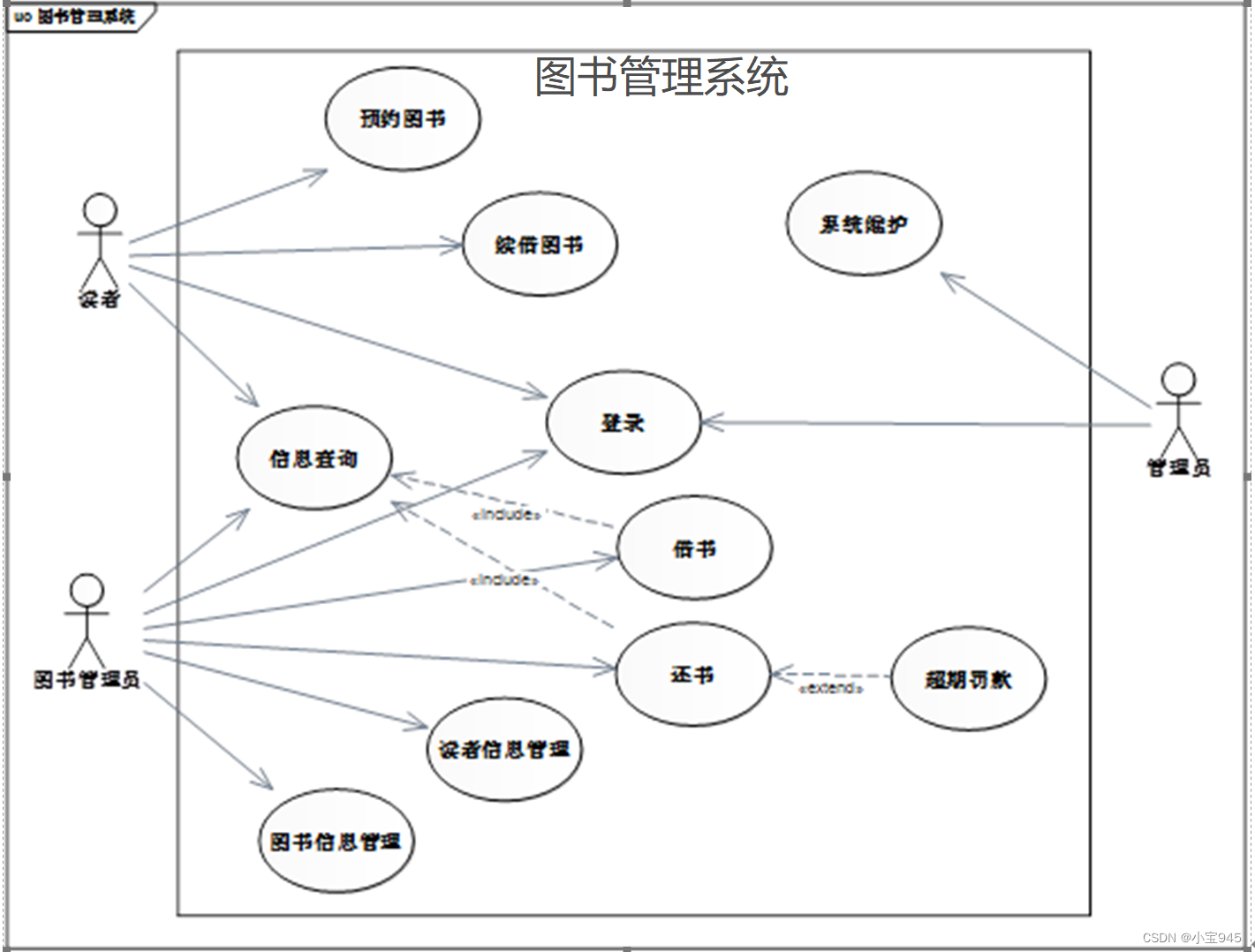
UML-用例图
提示:用例图是软件建模的开始,软件建模中的其他图形都将以用例图为依据。用例图列举了系统所需要实现的所有功能,除了用于软件开发的需求分析阶段,也可用于软件的系统测试阶段。 UML-用例图 一、用例图的基础知识1.用例图的构成元…...
jmeter--8.加密传输
目录 1. Base64加密 2. MD5加密 3. SHA加密(sha1\sha\sha224\sha256\sha384\sha512) 4. RSA加密-公钥加密,私钥解密 1. Base64加密 1.1 在需要加密传输的接口下新增BeanShell 预处理程序,${username}可替换成value值ÿ…...

微信小程序canvas画布转图片转pdf文件
关键步骤介绍 步骤一:将canvas页面保存为图片 for(var a=0;a<this.data.page_canvas.length;++a){ var t_page_img = await this.canvas_to_image(this.data.page_canvas[a]) t_img.push(t_page_img) } this.data.page_canvas是保存的canvas界面,this.c…...
【Linux操作】国产Linux服务管理操作
【Linux操作】国产Linux服务管理操作 前言SAMBA配置服务器端1. 安装相关包2. 配置/etc/samba/smb.conf,在此文件末尾添加如下内容,并保存退出。3. 创建/home/share并更改权限4. 启动samba服务 客户端• Windows客户端• 麒麟客户端 Telnet1、telnet语法2…...

大语言模型系列-word2vec
文章目录 前言一、word2vec的网络结构和流程1.Skip-Gram模型2.CBOW模型 二、word2vec的训练机制1. Hierarchical softmax2. Negative Sampling 总结 前言 在前文大语言模型系列-总述已经提到传统NLP的一般流程: 创建语料库 > 数据预处理 > 分词向量化 > …...

vue项目运行报错this[kHandle] = new _Hash(algorithm, xofLen)
自从昨天分盘重装了最新版本的Node之后,项目是一启一个报错 出现这个报错时,需要在package.json文件中 dev命令行 增加:set NODE_OPTIONS–openssl-legacy-provider 出现该问题的原因: node.js V17开始版本中发布的是OpenSSL3.0,…...

APP兼容性测试,这几个面试硬技能,包教包会
兼容性测试主要通过人工或自动化的方式,在需要覆盖的终端设备上进行功能用例执行,查看软件性能、稳定性等是否正常。 对于需要覆盖的终端设备,大型互联网公司,像 BAT,基本都有自己的测试实验室,拥有大量终…...

【学习iOS高质量开发】——熟悉Objective-C
文章目录 一、Objective-C的起源1.OC和其它面向对象语言2.OC和C语言3.要点 二、在类的头文件中尽量少引用其他头文件1.OC的文件2.向前声明的好处3.如何正确引入头文件4.要点 三、多用字面量语法,少用与之等价的方法1.何为字面量语法2.字面数值3.字面量数组4.字面量字…...
Qt/QML编程之路:Grid、GridLayout、GridView、Repeater(33)
GRID网格用处非常大,不仅在excel中,在GUI中,也是非常重要的一种控件。 Grid 网格是一种以网格形式定位其子项的类型。网格创建一个足够大的单元格网格,以容纳其所有子项,并将这些项从左到右、从上到下放置在单元格中。每个项目都位于其单元格的左上角,位置为(0,0)。…...
mac pro “RESP.app”意外退出 redis desktop manager
文章目录 redis desktop manager下载地址提示程序含有恶意代码“RESP.app”意外退出解决办法:下载python3.10.并安装重新打开RESP如果还是不行,那么需要替换错误路径(我的没用)外传 最近在研究redis的消息,看到了strea…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

Python爬虫(52)Scrapy-Redis分布式爬虫架构实战:IP代理池深度集成与跨地域数据采集
目录 一、引言:当爬虫遭遇"地域封锁"二、背景解析:分布式爬虫的两大技术挑战1. 传统Scrapy架构的局限性2. 地域限制的三种典型表现 三、架构设计:Scrapy-Redis 代理池的协同机制1. 分布式架构拓扑图2. 核心组件协同流程 四、技术实…...
