【学习笔记】[AGC063E] Child to Parent
提供一个多项式做法。
分别设 f u , i , g u , i f_{u,i},g_{u,i} fu,i,gu,i表示以 u u u为根时, a u = i a_u=i au=i和 a u ≥ i a_u\ge i au≥i的方案数,合并子树 v v v时,转移如下:
f u , i = ∑ f u , i − k r × g v . k f_{u,i}=\sum f_{u,i-kr}\times g_{v.k} fu,i=∑fu,i−kr×gv.k
初值为 f u , a u = 1 f_{u,a_u}=1 fu,au=1。
注意到 DP 的值域很大,通常情况下我们可以考虑用拉格朗日插值法来处理,但是实际上只要满足信息封闭也是可以转移的。我们不妨将其转化成多项式的形式,从而来观察需要记录哪些信息。
设:
F u ( x ) = ∑ f u , i x i G u ( x ) = ∑ g u , i x i F_u(x)=\sum f_{u,i}x^i\\G_u(x)=\sum g_{u,i}x^i Fu(x)=∑fu,ixiGu(x)=∑gu,ixi
转移大致分为以下几步:
F u ( x ) ← ∏ G v ( x ) F u ( x ) ← x a i F u ( x r ) G u ( x ) ← F u ( x ) + F u ( 1 ) − F u ( x ) 1 − x F_u(x)\gets \prod G_v(x)\\F_u(x)\gets x^{a_i}F_u(x^r)\\ G_u(x)\gets F_u(x)+\frac{F_u(1)-F_u(x)}{1-x} Fu(x)←∏Gv(x)Fu(x)←xaiFu(xr)Gu(x)←Fu(x)+1−xFu(1)−Fu(x)
其中最后一个式子是在求后缀和,之所以不能写成 1 1 − x − 1 \frac{1}{1-x^{-1}} 1−x−11的原因是生成函数不能有次数 < 0 <0 <0的项。
现在问题在于,要求出 F u ( 1 ) F_u(1) Fu(1)就必须维护各项系数,显然次数太高就寄了。考虑一步非常巧妙的转化:我们设 G u ′ ( x ) = G u ( x + 1 ) , F u ′ ( x ) = F u ( x + 1 ) G'_u(x)=G_u(x+1),F'_u(x)=F_u(x+1) Gu′(x)=Gu(x+1),Fu′(x)=Fu(x+1),则 F u ′ ( 0 ) = F u ( 1 ) F'_u(0)=F_u(1) Fu′(0)=Fu(1),而 F u ′ ( 0 ) F'_u(0) Fu′(0)其实就是常数项,又因为要求的答案也是常数项,这样我们只用算次数较低的项,信息就封闭了。
新的转移大致为:
F u ′ ( x ) ← ∏ G v ′ ( x ) F'_u(x)\gets \prod G'_v(x)\\ Fu′(x)←∏Gv′(x)
这是因为
F u ′ ( x ) = F u ( x + 1 ) = ∏ G v ( x + 1 ) = ∏ G v ′ ( x ) F'_u(x)=F_u(x+1)=\prod G_v(x+1)=\prod G'_v(x) Fu′(x)=Fu(x+1)=∏Gv(x+1)=∏Gv′(x)
F u ′ ( x ) ← ( x + 1 ) a i F u ′ ( ( x + 1 ) r − 1 ) F_u'(x)\gets (x+1)^{a_i}F_u'((x+1)^r-1) Fu′(x)←(x+1)aiFu′((x+1)r−1)
这是因为
F u ′ ( x ) = F u ( x + 1 ) = ( x + 1 ) a i F u ( ( x + 1 ) r ) = ( x + 1 ) a i F u ′ ( ( x + 1 ) r − 1 ) F'_u(x)=F_u(x+1)=(x+1)^{a_i}F_u((x+1)^r)=(x+1)^{a_i}F_u'((x+1)^r-1) Fu′(x)=Fu(x+1)=(x+1)aiFu((x+1)r)=(x+1)aiFu′((x+1)r−1)
G u ′ ( x ) = F u ′ ( x ) + F u ′ ( 0 ) − F u ′ ( x ) − x G'_u(x)=F'_u(x)+\frac{F'_u(0)-F'_u(x)}{-x} Gu′(x)=Fu′(x)+−xFu′(0)−Fu′(x)
如果我们只保留前 k k k项,那么因为要除以 x x x,所以每次转移完后最后一项都会损失掉。但是因为答案是第一项的值,所以我们对于每个节点保留 d e p u dep_u depu项即可。
复杂度 O ( n 3 ) O(n^3) O(n3)。
麻了,好像和官方题解长得一样。
#include<bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define inf 0x3f3f3f3f
#define ll long long
using namespace std;
const int mod=998244353;
int n,fa[305],dep[305];
ll r,fac[305],inv[305],ifac[305],to[305][305],f[305][305],g[305][305],a[305],res;
vector<int>G[305];
ll fpow(ll x,ll y=mod-2){ll z(1);for(;y;y>>=1){if(y&1)z=z*x%mod;x=x*x%mod;}return z;
}
ll binom(int x,int y){if(x<0||y<0||x<y)return 0;return fac[x]*inv[y]%mod*inv[x-y]%mod;
}
void init(int n){fac[0]=1;for(int i=1;i<=n;i++)fac[i]=fac[i-1]*i%mod;inv[n]=fpow(fac[n]);for(int i=n;i>=1;i--)inv[i-1]=inv[i]*i%mod;ifac[1]=1;for(int i=2;i<=n;i++)ifac[i]=mod-ifac[mod%i]*(mod/i)%mod;
}
void dfs(int u){f[u][0]=1;for(auto v:G[u]){dep[v]=dep[u]+1,dfs(v);memset(f[0],0,sizeof f[0]);for(int i=0;i<=dep[v];i++)for(int j=0;i+j<=dep[v];j++)(f[0][i+j]+=f[u][i]*g[v][j])%=mod;memcpy(f[u],f[0],sizeof f[0]);}memset(f[0],0,sizeof f[0]);for(int i=0;i<=dep[u]+1;i++)for(int j=0;j<=dep[u]+1;j++)(f[0][j]+=f[u][i]*to[i][j])%=mod;memset(f[u],0,sizeof f[u]);ll mul=1;for(int i=0;i<=dep[u]+1;i++){for(int j=0;i+j<=dep[u]+1;j++)(f[u][i+j]+=mul*f[0][j])%=mod;mul=mul*(a[u]-i)%mod*ifac[i+1]%mod;}for(int i=0;i<=dep[u];i++)g[u][i]=(f[u][i]+f[u][i+1])%mod;
}
signed main(){//freopen("data.in","r",stdin);ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n;for(int i=2;i<=n;i++)cin>>fa[i],G[fa[i]].pb(i);cin>>r;init(n);to[0][0]=1;for(int i=1;i<=n;i++){for(int j=0;j<=i;j++){ll mul=1;int sgn=(i-j&1)?-1:1;for(int k=0;k<=n;k++){(to[i][k]+=sgn*binom(i,j)*mul)%=mod;mul=mul*((j*r-k)%mod)%mod*ifac[k+1]%mod;}}}for(int i=1;i<=n;i++)cin>>a[i];dfs(1);cout<<(f[1][0]+mod)%mod;
}
相关文章:

【学习笔记】[AGC063E] Child to Parent
提供一个多项式做法。 分别设 f u , i , g u , i f_{u,i},g_{u,i} fu,i,gu,i表示以 u u u为根时, a u i a_ui aui和 a u ≥ i a_u\ge i au≥i的方案数,合并子树 v v v时,转移如下: f u , i ∑ f u , i − k r g v . k…...

sar 运行出错
手机上使用sar 使用sar工具报错 / # sar -I SUM 1 1 Cannot find the data collector (sadc) exec: No such file or directory Inconsistent input data解决方法:需要将 sadc sadf sar 三个bin同时推到/usr/bin/目录下 / # sar -I SUM 1 2 Linux 5.15.104-ab558…...

UE5 C++的TCP服务器与客户端
客户端.h 需要在Build.cs中加入模块:"Networking","Sockets","Json","JsonUtilities" // Fill out your copyright notice in the Description page of Project Settings.#pragma once#include "CoreMinimal.h" #include…...
nginx+lua配置,一个域名配置https,docker集群使用
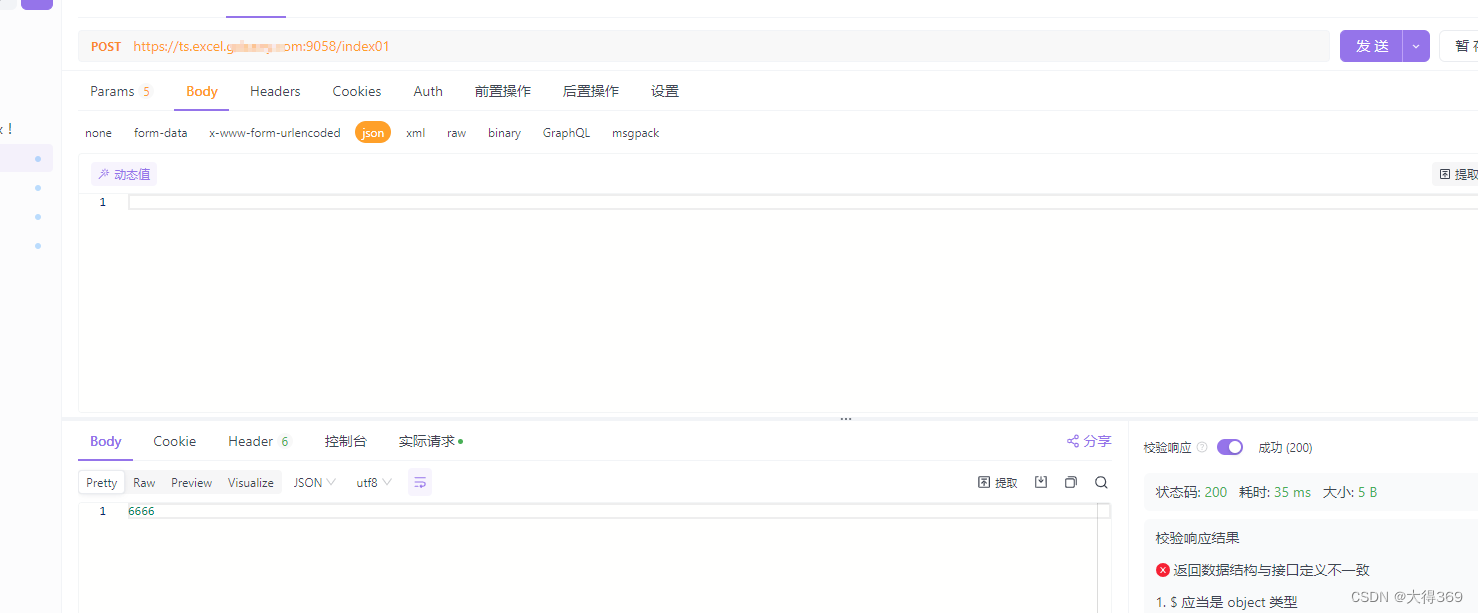
没安装kua的先安装lua 没有resty.http模块的,许配置 nginxlua配置,一个域名配置https,docker集群使用,一个域名配置https管理整个集群 lua做转发(方向代理) 1、ad_load.lua文件 ngx.header.content_typ…...

jQuery 正则表达式 验证表单
文章目录 简介:什么是正则表达式以及作用:●文本框内容的验证:代码演示示例: 简介: jQuery Form插件是一个优秀的Ajax表单插件,可以非常容易地、无侵入地升级HTML表单以支持Ajax。jQuery Form有两个核心方法…...
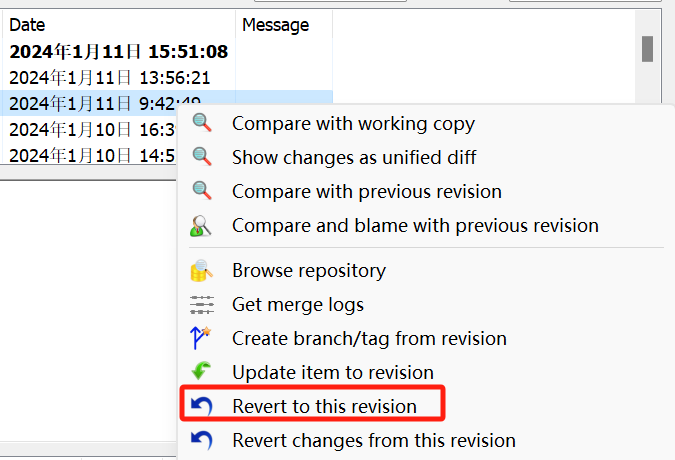
如何使用SVN查看旧版本
和目录 第一步:打开SVN客户端 第二步:浏览历史版本 第三步:还原历史版本 结论 Subversion (缩写为SVN)是一种常用的版本控制系统,它可以帮助团队协作开发软件项目。除了基本的版本控制功能外,SVN还提供了许多其他功…...
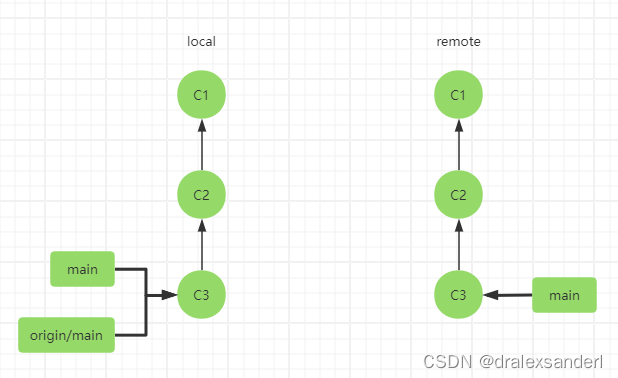
使用 GitHub 远程仓库
使用 GitHub 远程仓库 GitHub 是最大的 Git 版本库托管商,是成千上万的开发者和项目能够合作进行的中心。 大部分 Git 版本库都托管在 GitHub,很多开源项目使用 GitHub 实现 Git 托管、问题追踪、代码审查以及其它事情。本篇文章主要带大家上手 GitHub …...

关键词提取
在自然语言处理领域中,处理海量文本信息的关键在于把用户关心的问题提取出来。而关键词是能够表达文档中心内容的词语,更是表达文档主题的最小单位。因此,文本关键词的提取对于文本信息的理解是至关重要的。 关键词提取是文本挖掘领域下的一个…...
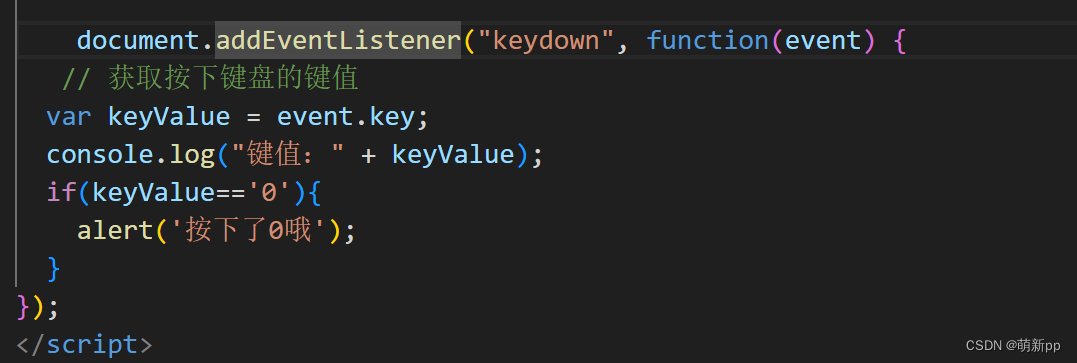
web开发学习笔记(2.js)
1.引入 2.js的两种引入方式 3.输出语句 4.全等运算符 5.定义函数 6.数组 7.数组属性 8.字符串对象的对应方法 9.自定义对象 10.json对象 11.bom属性 12.window属性 13.定时刷新时间 14.跳转网址 15.DOM文档对象模型 16.获取DOM对象,根据DOM对象来操作网页 如下图…...
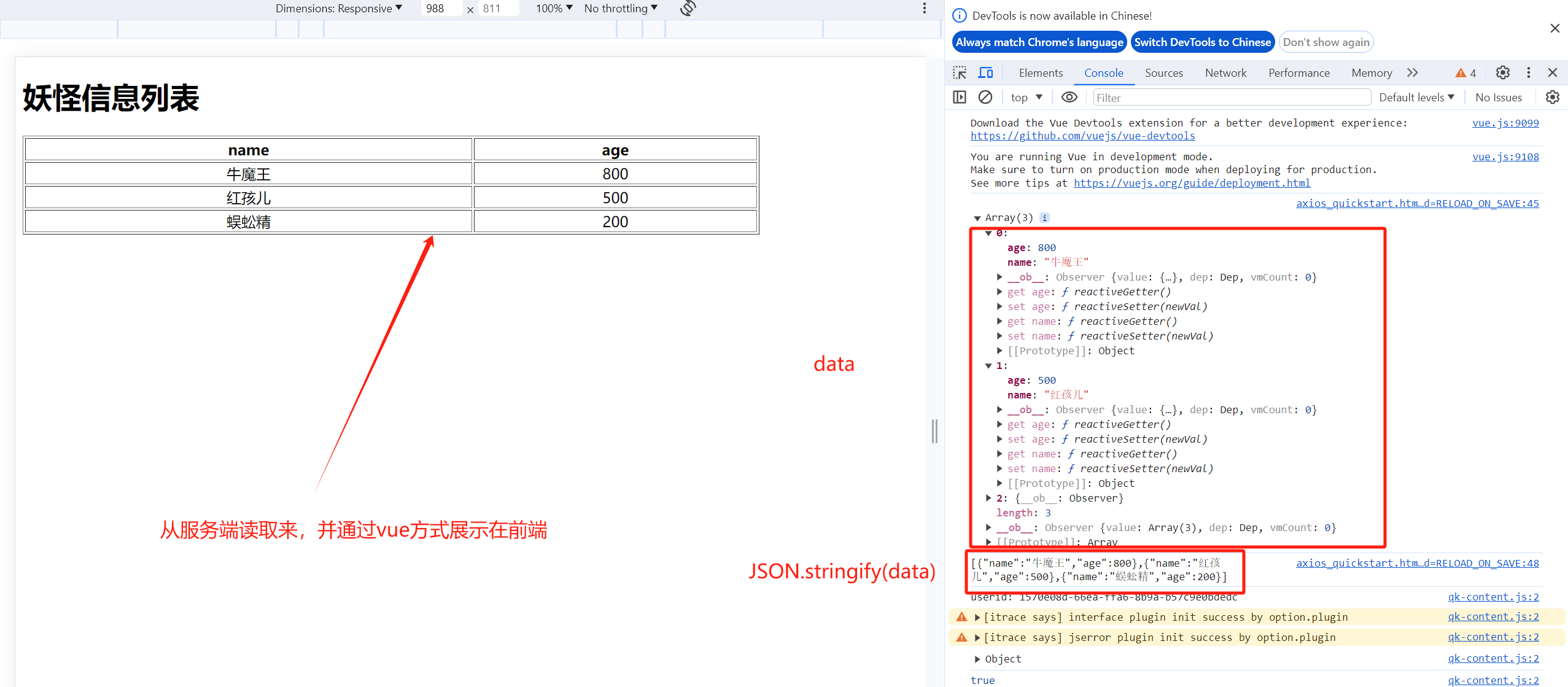
Vue Axios——前端技术栈
文章目录 基本介绍Vue是什么? MVVMVue的使用快速入门注意事项和使用细节 Vue 数据绑定机制分析数据单向渲染注意事项和细节 双向数据绑定事件绑定示例:注意事项和使用细节课后作业1课后作业2 修饰符示例 条件渲染/控制: v-if v-showv-if VS v-show课后作…...
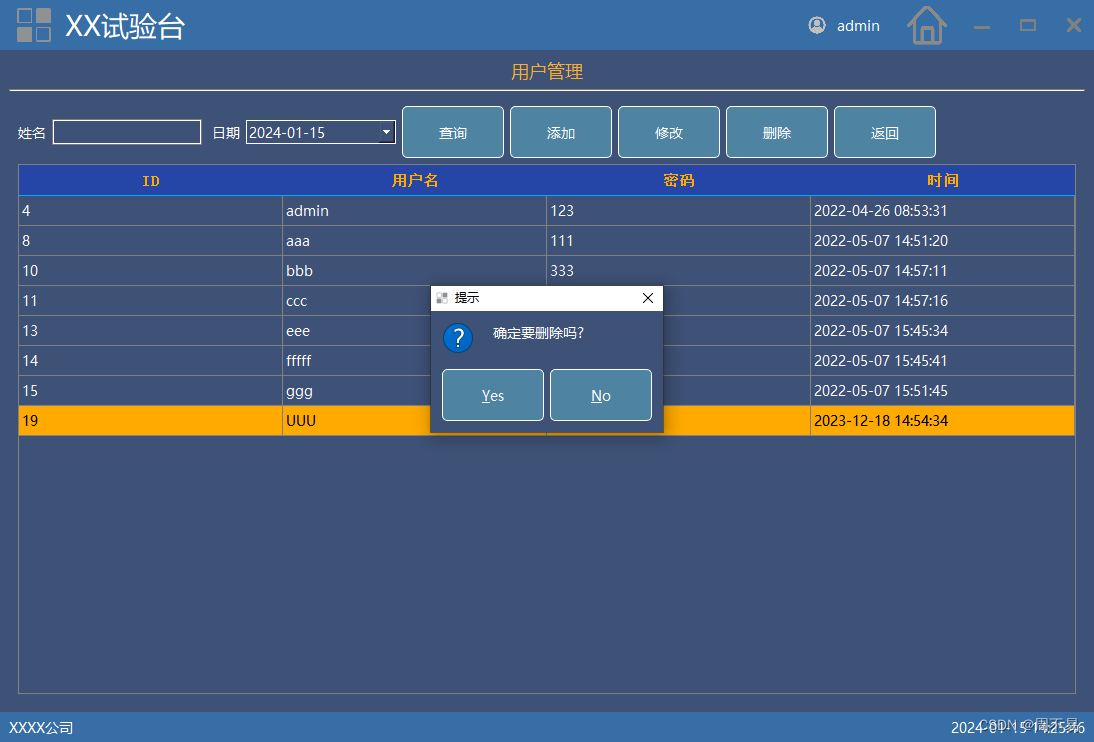
九、Qt C++ 数据库开发
《一、QT的前世今生》 《二、QT下载、安装及问题解决(windows系统)》《三、Qt Creator使用》 《四、Qt 的第一个demo-CSDN博客》 《五、带登录窗体的demo》 《六、新建窗体时,几种窗体的区别》 《七、Qt 信号和槽》 《八、Qt C 毕业设计》 《九、Qt …...

力扣电话号码的组合
文章目录 题目说明做题思路代码实现代码解析 题目链接 题目说明 首先我们先分析一下这个题目题目中说呢先给出一个字符串这个字符串其实就是这个九键数字我们要按照要求将数字所代表的字符进行自由组合形成一个字符串并且这个字符串的长度和输入的数字字符串长度相同࿰…...

ZooKeeper 实战(五) Curator实现分布式锁
文章目录 ZooKeeper 实战(五) Curator实现分布式锁1.简介1.1.分布式锁概念1.2.Curator 分布式锁的实现方式1.3.分布式锁接口 2.准备工作3.分布式可重入锁3.1.锁对象3.2.非重入式抢占锁测试代码输出日志 3.3.重入式抢占锁测试代码输出日志 4.分布式非可重入锁4.1.锁对象4.2.重入…...

基于kubernetes部署MySQL主从环境
部署方式 通过部署mysql主从容器,配置主从pod之间数据同步。 配置数据库访问的密码 创建 Mysql 密码的 Secret [rootk8s-master1 master]# kubectl create secret generic mysql-password --namespaceapp --from-literalmysql_root_passwordroot secret/mysql-pas…...

【JAVA语言-第13话】异常处理 之 try-catch-finally,throws,throw关键字的详细解析
目录 异常处理 1.1 概述 1.2 异常分类 1.3 异常处理 1.3.1 throws 1.3.2 try-catch 1.3.3 finally代码块 1.3.4 throw关键字 1.3.5 throw和throws的区别 1.4 自定义异常 1.4.1 概述 1.4.2 定义 1.4.3 自定义异常练习 异常处理 1.1 概述 在Java中,异常…...

ChatGPT4.0 >ChatGPT 3.5 > 文心一言
文章目录 前言一、ChatGPT4.0与ChatGPT3.5相比具有以下优点:二、ChatGPT和文心一言相比具有以下优点:总结 前言 ChatGPT是一种基于自然语言处理的对话型人工智能模型,由OpenAI开发。它是使用了大规模的语料库进行无监督学习的结果࿰…...

Linux 入门命令大全汇总 + Linux 集锦大全 【20240115】
文章目录 Linux 入门命令大全汇总Linux 集锦大全更多信息 Linux 入门命令大全汇总 别有一番风趣的alias 刚刚好合适的 apropos 命令 迷你计算器 bc 可看黄道吉日的 cal 全文可查看: Linux入门命令大全全文 Linux 集锦大全 linux终端中最漂亮的几款字体介绍及…...

【Web】NSSCTF Round#16 Basic个人wp(全)
出题友好,适合手生复健。 目录 ①RCE但是没有完全RCE ②了解过PHP特性吗 ①RCE但是没有完全RCE 上来就是一段md5八股 (string)就是不让用数组了,然后强比较需要md5碰撞 ?md5_1%4d%c9%68%ff%0e%e3%5c%20%95%72%d4%77%7b%72%15%87%d3%6f%a7%b2%1b%dc…...

【目标跟踪】跨相机如何匹配像素
文章目录 前言一、计算思路二、代码三、结果 前言 本本篇博客介绍一种非常简单粗暴的方法,做到跨相机像素匹配。已知各相机内外参,计算共视区域像素投影(不需要计算图像特征)。废话不多说,直接来,见下图。…...

Python 发微信:实现自动化沟通的利器
引言: 在当今信息爆炸的时代,微信已经成为人们日常生活中不可或缺的沟通工具。然而,手动发送微信消息往往耗时耗力,尤其是在需要频繁发送消息的场景下。为了提高工作效率和便利性,我们可以利用 Python 编程语言来实现自…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...
