2024美赛数学建模思路 - 案例:ID3-决策树分类算法
文章目录
- 0 赛题思路
- 1 算法介绍
- 2 FP树表示法
- 3 构建FP树
- 4 实现代码
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 算法介绍
FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模式树算法,他与Apriori算法一样也是用来挖掘频繁项集的,不过不同的是,FP-Tree算法是Apriori算法的优化处理,他解决了Apriori算法在过程中会产生大量的候选集的问题,而FP-Tree算法则是发现频繁模式而不产生候选集。但是频繁模式挖掘出来后,产生关联规则的步骤还是和Apriori是一样的。
常见的挖掘频繁项集算法有两类,一类是Apriori算法,另一类是FP-growth。Apriori通过不断的构造候选集、筛选候选集挖掘出频繁项集,需要多次扫描原始数据,当原始数据较大时,磁盘I/O次数太多,效率比较低下。FPGrowth不同于Apriori的“试探”策略,算法只需扫描原始数据两遍,通过FP-tree数据结构对原始数据进行压缩,效率较高。
FP代表频繁模式(Frequent Pattern) ,算法主要分为两个步骤:FP-tree构建、挖掘频繁项集。
2 FP树表示法
FP树通过逐个读入事务,并把事务映射到FP树中的一条路径来构造。由于不同的事务可能会有若干个相同的项,因此它们的路径可能部分重叠。路径相互重叠越多,使用FP树结构获得的压缩效果越好;如果FP树足够小,能够存放在内存中,就可以直接从这个内存中的结构提取频繁项集,而不必重复地扫描存放在硬盘上的数据。
一颗FP树如下图所示:
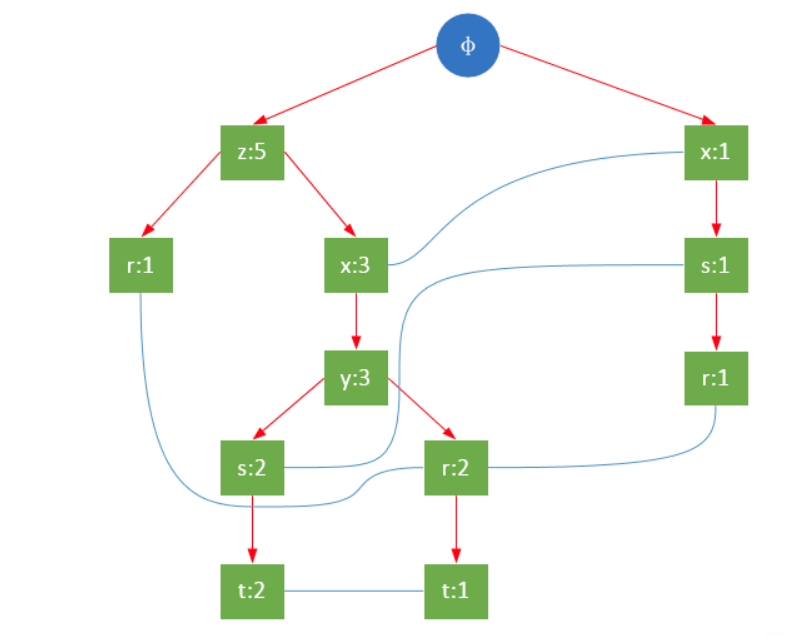
通常,FP树的大小比未压缩的数据小,因为数据的事务常常共享一些共同项,在最好的情况下,所有的事务都具有相同的项集,FP树只包含一条节点路径;当每个事务都具有唯一项集时,导致最坏情况发生,由于事务不包含任何共同项,FP树的大小实际上与原数据的大小一样。
FP树的根节点用φ表示,其余节点包括一个数据项和该数据项在本路径上的支持度;每条路径都是一条训练数据中满足最小支持度的数据项集;FP树还将所有相同项连接成链表,上图中用蓝色连线表示。
为了快速访问树中的相同项,还需要维护一个连接具有相同项的节点的指针列表(headTable),每个列表元素包括:数据项、该项的全局最小支持度、指向FP树中该项链表的表头的指针。
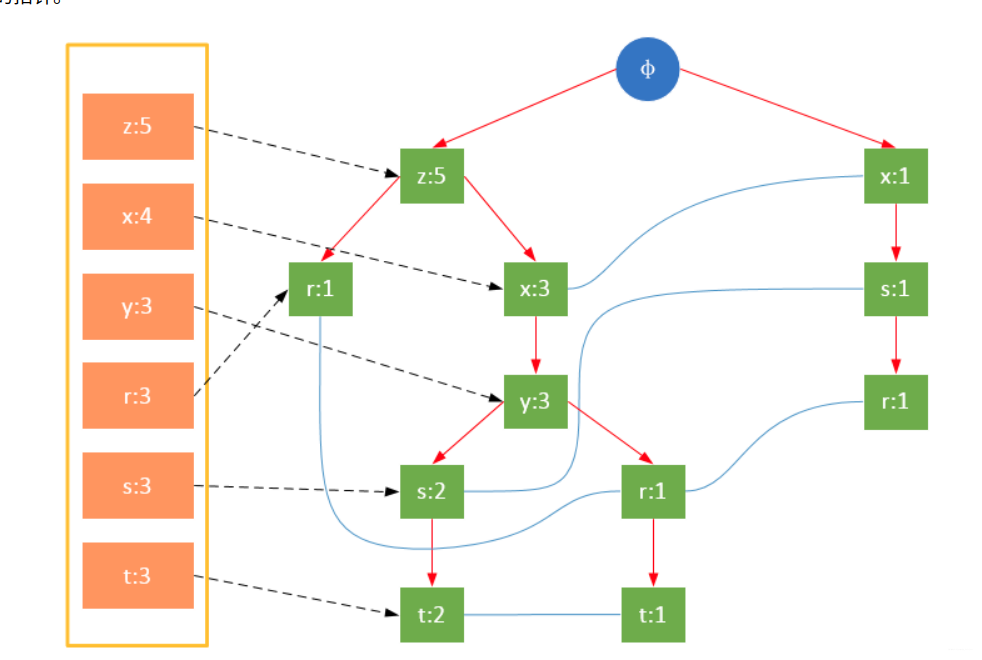
3 构建FP树
现在有如下数据:
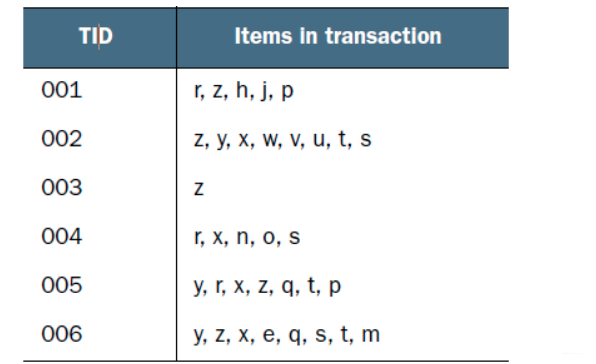
FP-growth算法需要对原始训练集扫描两遍以构建FP树。
第一次扫描,过滤掉所有不满足最小支持度的项;对于满足最小支持度的项,按照全局最小支持度排序,在此基础上,为了处理方便,也可以按照项的关键字再次排序。
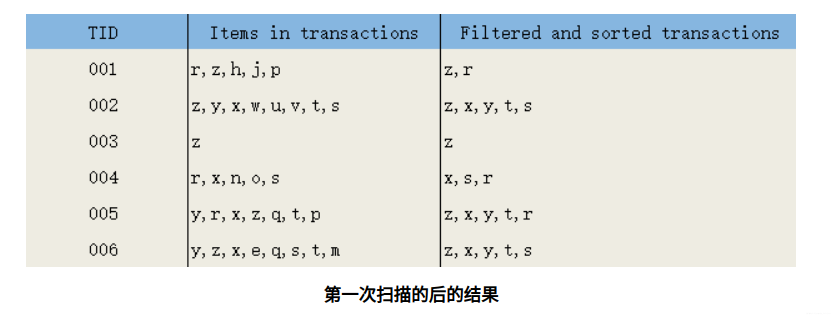
第二次扫描,构造FP树。
参与扫描的是过滤后的数据,如果某个数据项是第一次遇到,则创建该节点,并在headTable中添加一个指向该节点的指针;否则按路径找到该项对应的节点,修改节点信息。具体过程如下所示:
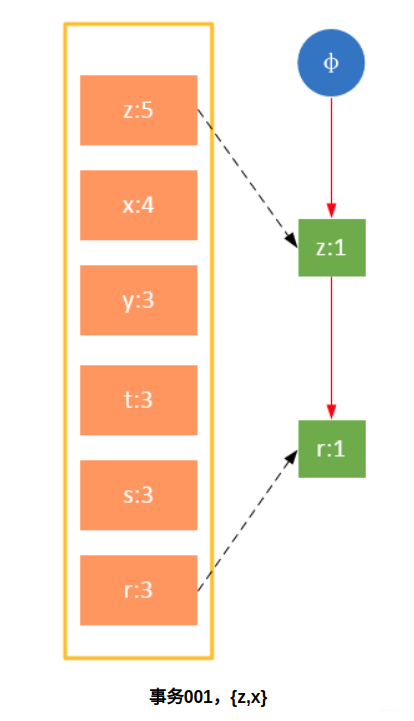
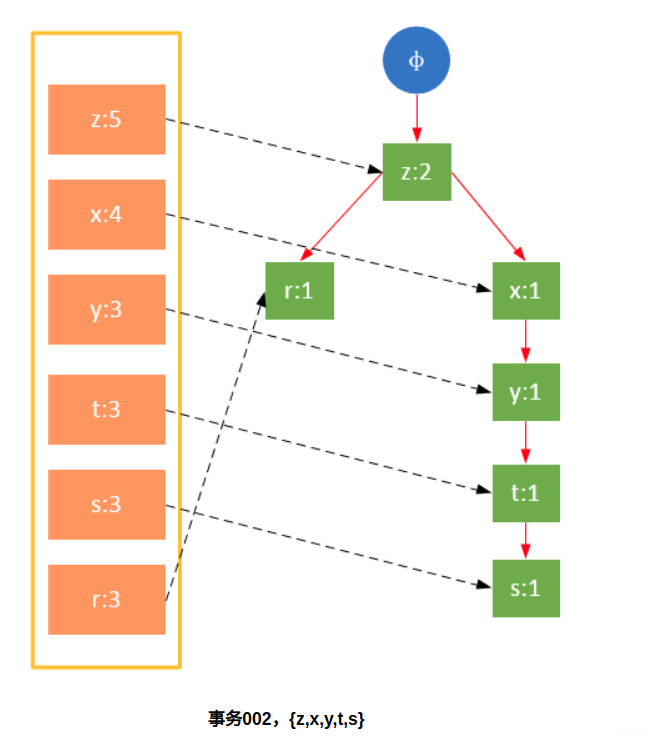
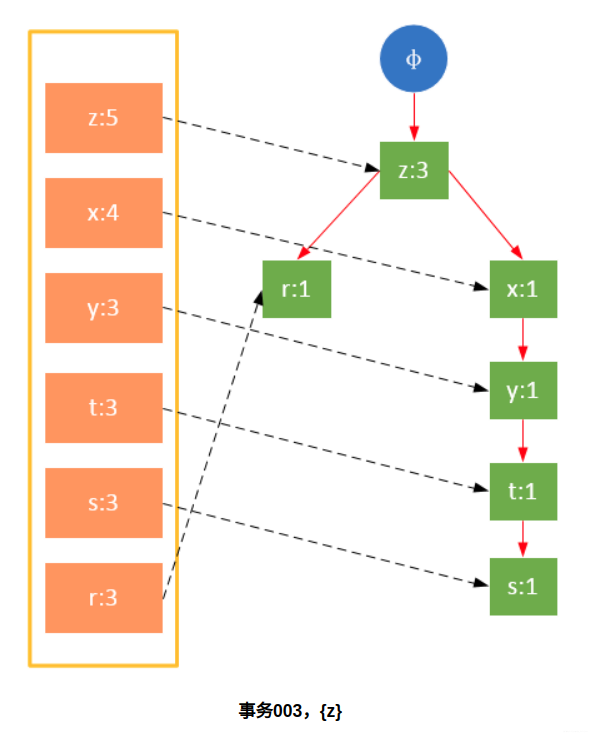
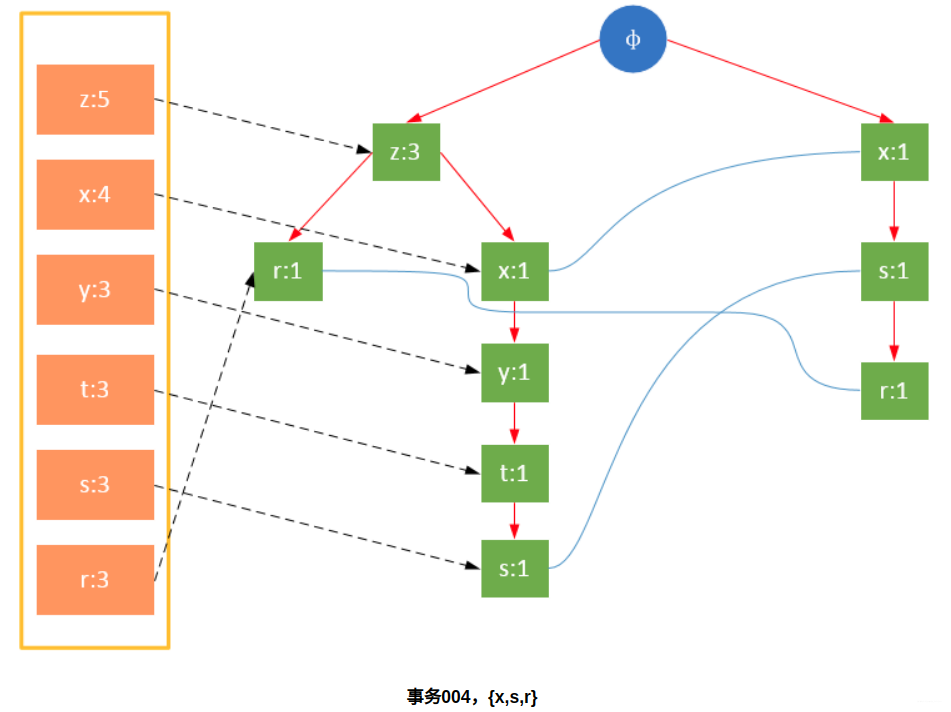
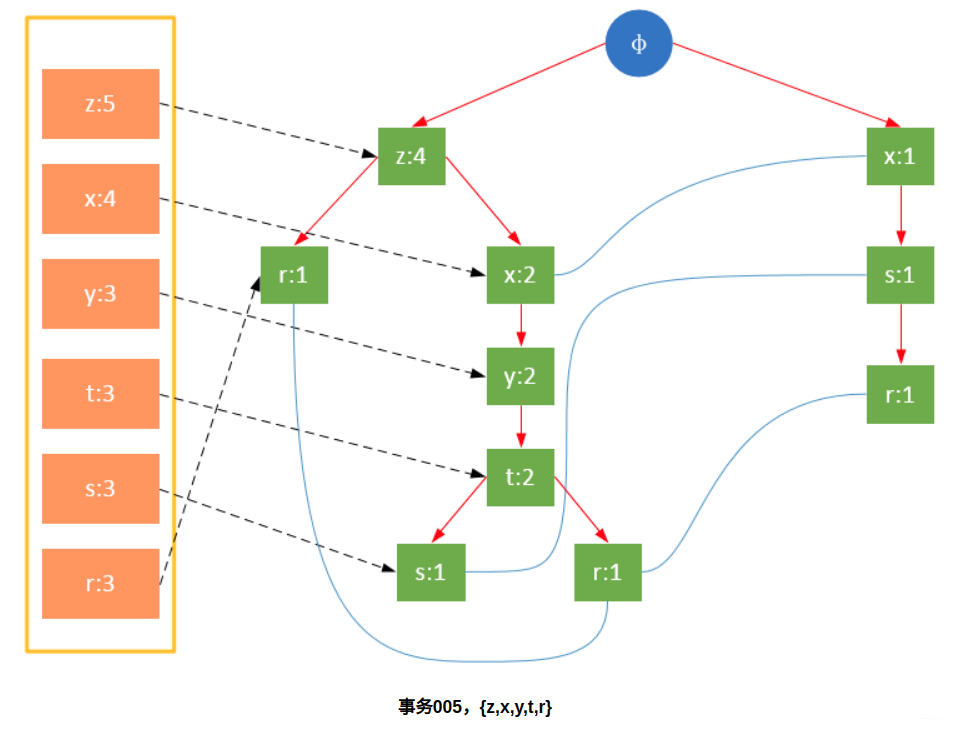
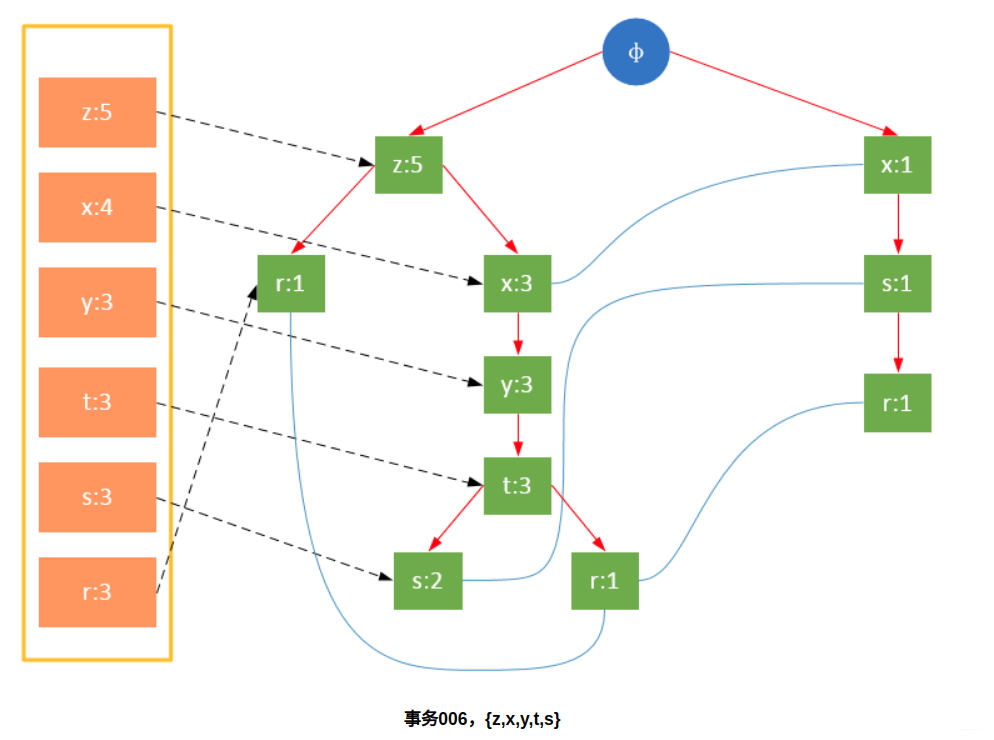
从上面可以看出,headTable并不是随着FPTree一起创建,而是在第一次扫描时就已经创建完毕,在创建FPTree时只需要将指针指向相应节点即可。从事务004开始,需要创建节点间的连接,使不同路径上的相同项连接成链表。
4 实现代码
def loadSimpDat():simpDat = [['r', 'z', 'h', 'j', 'p'],['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],['z'],['r', 'x', 'n', 'o', 's'],['y', 'r', 'x', 'z', 'q', 't', 'p'],['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]return simpDatdef createInitSet(dataSet):retDict = {}for trans in dataSet:fset = frozenset(trans)retDict.setdefault(fset, 0)retDict[fset] += 1return retDictclass treeNode:def __init__(self, nameValue, numOccur, parentNode):self.name = nameValueself.count = numOccurself.nodeLink = Noneself.parent = parentNodeself.children = {}def inc(self, numOccur):self.count += numOccurdef disp(self, ind=1):print(' ' * ind, self.name, ' ', self.count)for child in self.children.values():child.disp(ind + 1)def createTree(dataSet, minSup=1):headerTable = {}#此一次遍历数据集, 记录每个数据项的支持度for trans in dataSet:for item in trans:headerTable[item] = headerTable.get(item, 0) + 1#根据最小支持度过滤lessThanMinsup = list(filter(lambda k:headerTable[k] < minSup, headerTable.keys()))for k in lessThanMinsup: del(headerTable[k])freqItemSet = set(headerTable.keys())#如果所有数据都不满足最小支持度,返回None, Noneif len(freqItemSet) == 0:return None, Nonefor k in headerTable:headerTable[k] = [headerTable[k], None]retTree = treeNode('φ', 1, None)#第二次遍历数据集,构建fp-treefor tranSet, count in dataSet.items():#根据最小支持度处理一条训练样本,key:样本中的一个样例,value:该样例的的全局支持度localD = {}for item in tranSet:if item in freqItemSet:localD[item] = headerTable[item][0]if len(localD) > 0:#根据全局频繁项对每个事务中的数据进行排序,等价于 order by p[1] desc, p[0] descorderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: (p[1],p[0]), reverse=True)]updateTree(orderedItems, retTree, headerTable, count)return retTree, headerTabledef updateTree(items, inTree, headerTable, count):if items[0] in inTree.children: # check if orderedItems[0] in retTree.childreninTree.children[items[0]].inc(count) # incrament countelse: # add items[0] to inTree.childreninTree.children[items[0]] = treeNode(items[0], count, inTree)if headerTable[items[0]][1] == None: # update header tableheaderTable[items[0]][1] = inTree.children[items[0]]else:updateHeader(headerTable[items[0]][1], inTree.children[items[0]])if len(items) > 1: # call updateTree() with remaining ordered itemsupdateTree(items[1:], inTree.children[items[0]], headerTable, count)def updateHeader(nodeToTest, targetNode): # this version does not use recursionwhile (nodeToTest.nodeLink != None): # Do not use recursion to traverse a linked list!nodeToTest = nodeToTest.nodeLinknodeToTest.nodeLink = targetNodesimpDat = loadSimpDat()
dictDat = createInitSet(simpDat)
myFPTree,myheader = createTree(dictDat, 3)
myFPTree.disp()
上面的代码在第一次扫描后并没有将每条训练数据过滤后的项排序,而是将排序放在了第二次扫描时,这可以简化代码的复杂度。
控制台信息:

建模资料
资料分享: 最强建模资料


相关文章:

2024美赛数学建模思路 - 案例:ID3-决策树分类算法
文章目录 0 赛题思路1 算法介绍2 FP树表示法3 构建FP树4 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 算法介绍 FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模…...
GitHub图床搭建
1 准备Github账号 如果没有Github账号需要先在官网注册一个账号 2 创建仓库 在github上创建一个仓库,随便一个普通的仓库就行,选择公共仓库 并且配置github仓库的pages,选择默认访问的分支及默认路径 3 github token获取 github token创…...
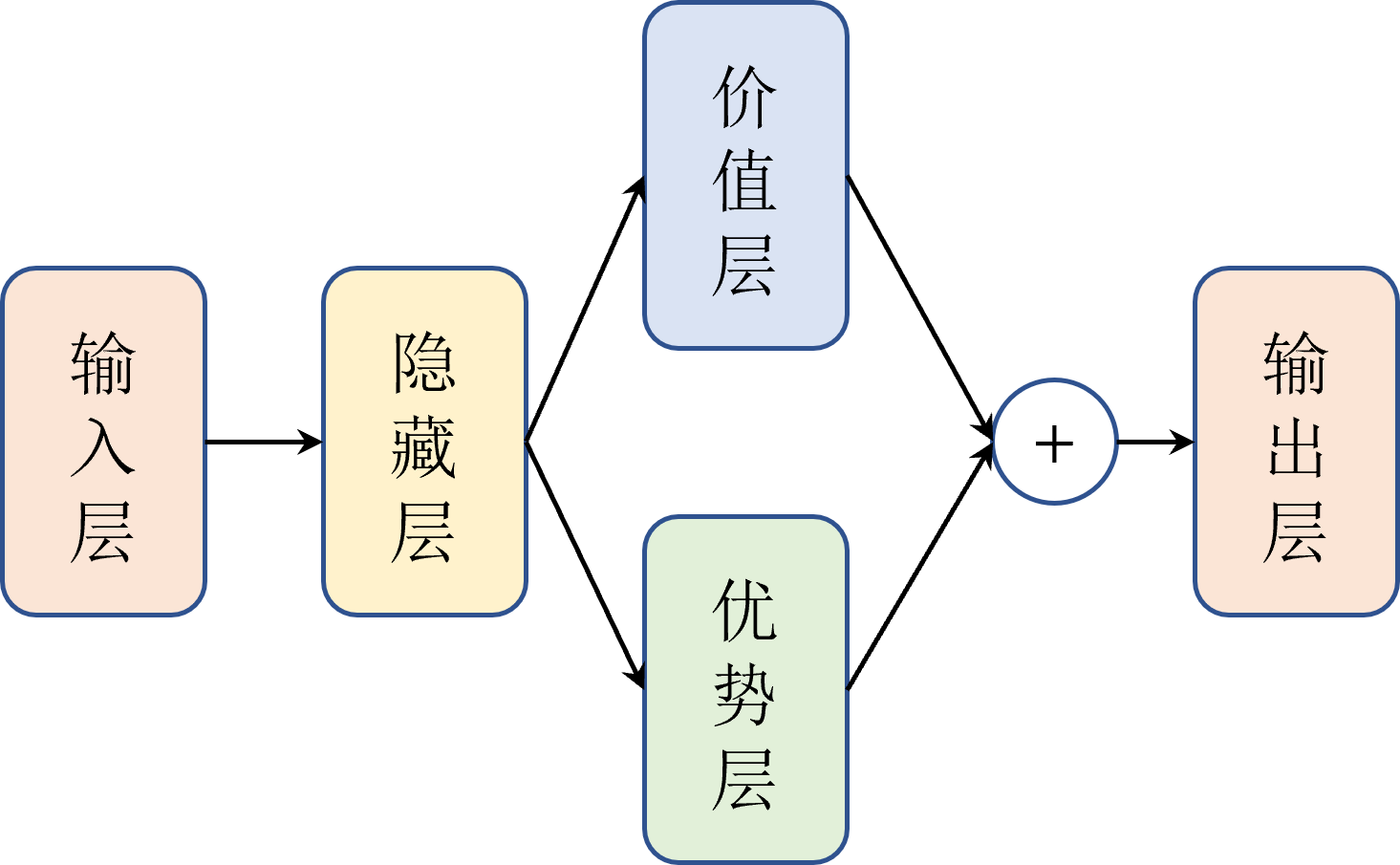
DQN、Double DQN、Dueling DQN、Per DQN、NoisyDQN 学习笔记
文章目录 DQN (Deep Q-Network)说明伪代码应用范围 Double DQN说明伪代码应用范围 Dueling DQN实现原理应用范围伪代码 Per DQN (Prioritized Experience Replay DQN)应用范围伪代码 NoisyDQN伪代码应用范围 部分内容与图片摘自:JoyRL 、 EasyRL DQN (Deep Q-Networ…...
C++ 编程需要什么样的开发环境?
C 编程需要什么样的开发环境? 在开始前我有一些资料,是我根据网友给的问题精心整理了一份「C的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!&#…...
—— 打字机效果)
Unity文字游戏开发日志(1)—— 打字机效果
作者是一名OIer,因为兴趣,想在寒假期间开发一款文字游戏的demo。 本博客仅用作记录,马蜂极度不符合规范。 但是,可以用来避坑。 1.等待功能——使用的是协程函数,且调用与常规调用函数不同。 private IEnumerator Sco(){isScoe…...
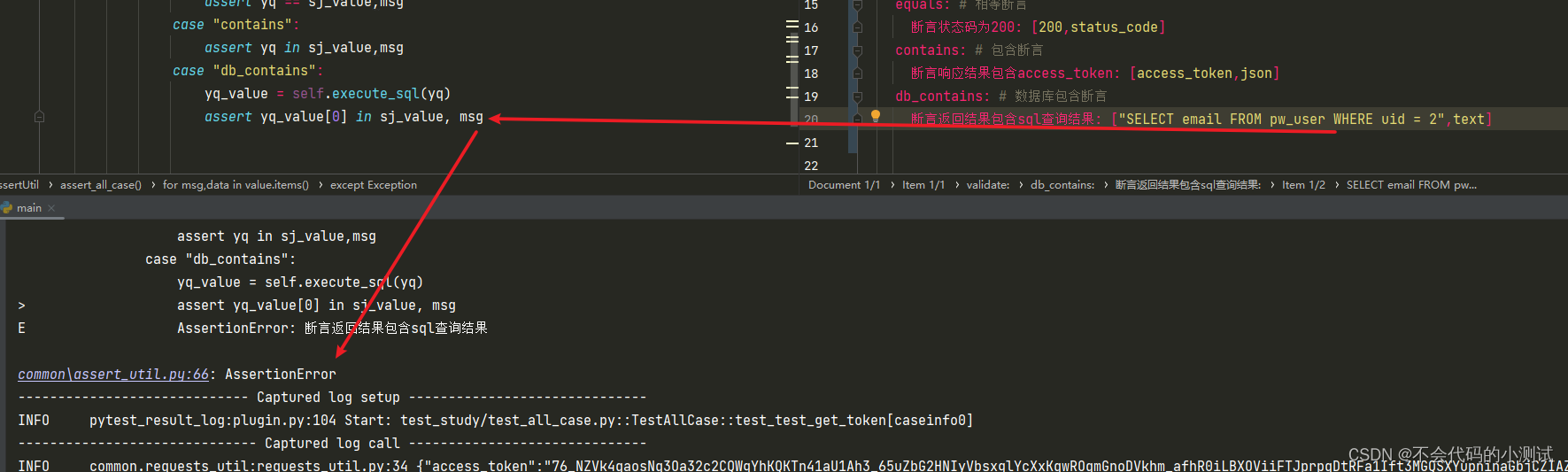
从0开始python学习-48.pytest框架之断言
目录 1. 响应进行断言 1.1 在yaml用例中写入断言内容 1.2 封装断言方法 1.3 在执行流程中加入断言判断内容 2. 数据库数据断言 2.1 在yaml用例中写入断言内容 2.2 连接数据库并封装执行sql的方法 2.3 封装后校验方法是否可执行 2.4 使用之前封装的断言方法,…...

学习JavaEE的日子 day13补 深入类加载机制及底层
深入类加载机制 初识类加载过程 使用某个类时,如果该类的class文件没有加载到内存时,则系统会通过以下三个步骤来对该类进行初始化 1.类的加载(Load) → 2.类的连接(Link) → 3.类的初始化(In…...
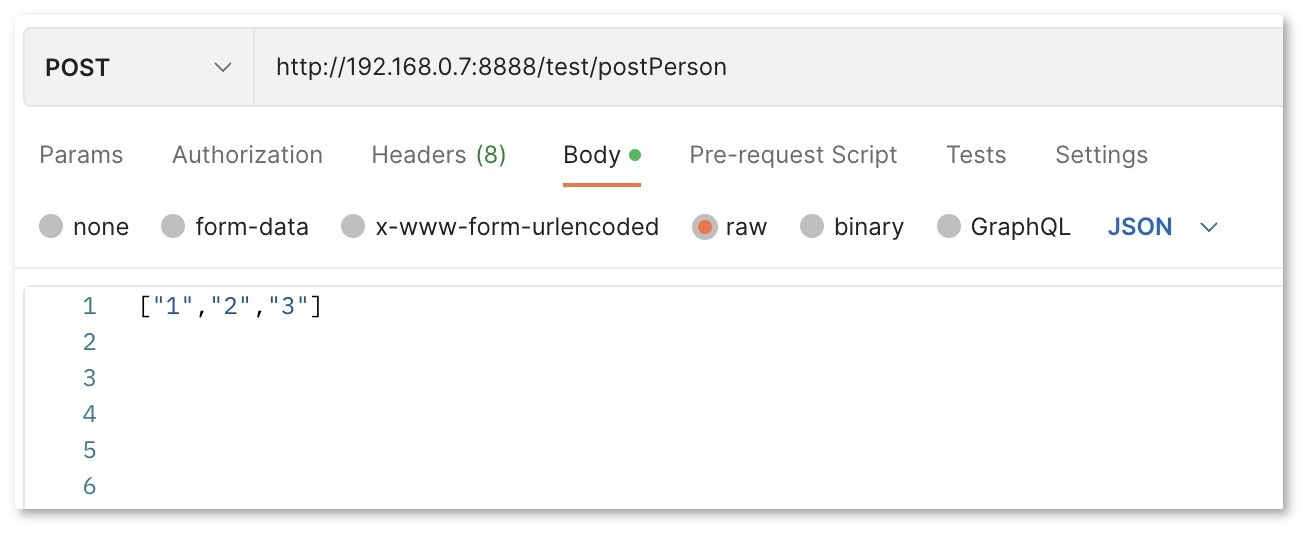
C# WebApi传参及Postman调试
概述 欢迎来到本文,本篇文章将会探讨C# WebApi中传递参数的方法。在WebApi中,参数传递是一个非常重要的概念,因为它使得我们能够从客户端获取数据,并将数据传递到服务器端进行处理。WebApi是一种使用HTTP协议进行通信的RESTful服…...

npm install 卡住不动的六种解决方法
1.重装 检查网络设置,删除node_modules重新npm install 2. 配置npm代理 // 配置nmp代理来提高速度,如设置淘宝镜像 npm config set registry https://registry.npm.taobao.org// 查看配置是否成功 npm config get registry// 成功后重新npm install安…...
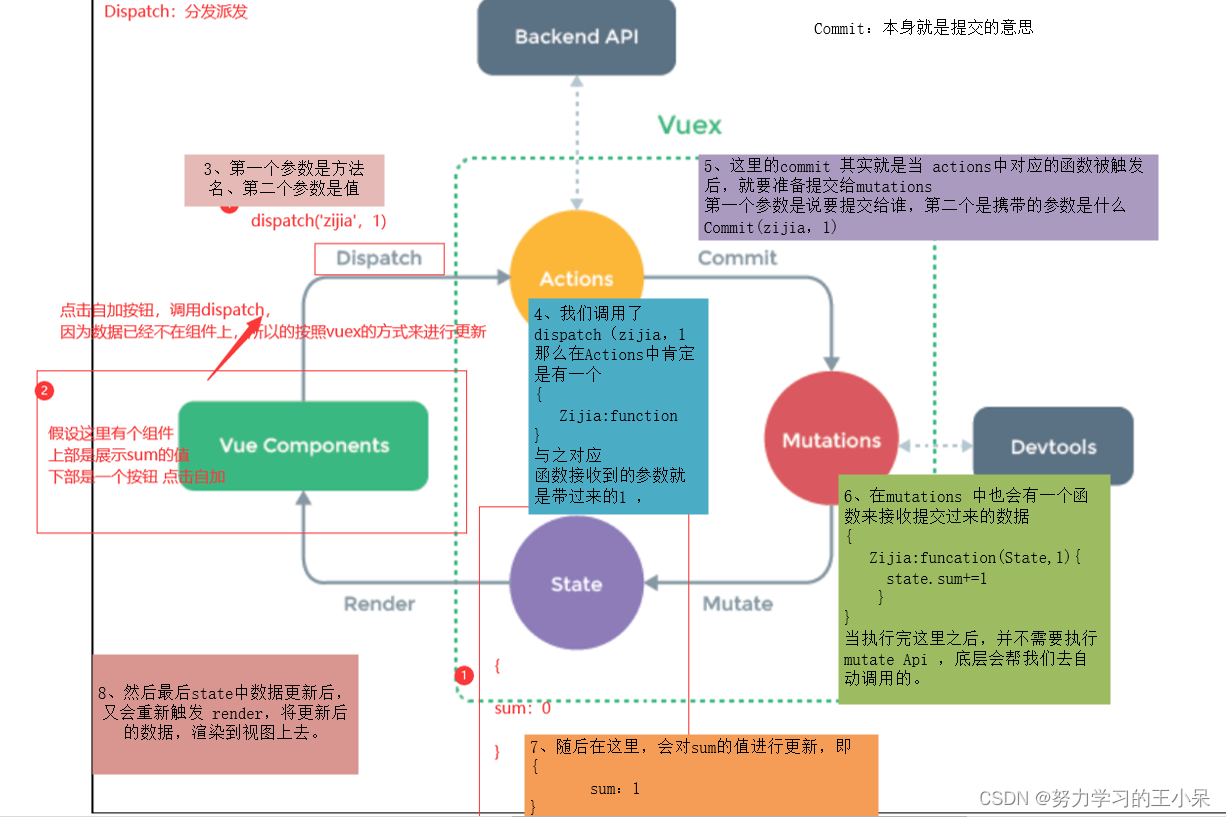
Vue高级(二)
3.搭建vuex环境 创建文件:src/store/index.js //引入Vue核心库import Vue from vue//引入Vueximport Vuex from vuex//应用Vuex插件Vue.use(Vuex)//准备actions对象——响应组件中用户的动作const actions {}//准备mutations对象——修改state中的数据const mutat…...

MongoDB面试系列-02
1. MongoDB 中必须调用 getLastError 来确保写操作生效吗? MongoDB中不管有没有调用getLastError(又称为Safe Mode),服务器执行的操作都会一样。 而调用getLastError只是为了确认写操作是否成功提交,但是写操作的安全…...

2024.1.17
今天我已经回家了,感觉家就像我的温柔乡一样,一到了家,就不想学习了,这是很不对的事情,不该如此堕落,还是要像在学校一样该干什么干什么,所以说还是复习和写了一下曾经写过的代码。 #define _C…...

openssl3.2 - 官方demo学习 - encrypt - rsa_encrypt.c
文章目录 openssl3.2 - 官方demo学习 - encrypt - rsa_encrypt.c概述笔记END openssl3.2 - 官方demo学习 - encrypt - rsa_encrypt.c 概述 从内存中的DER共钥数据构造pub_key, 用公钥加密明文, 输出密文. 非对称加密 从内存中的DER私钥数据构造priv_key, 用私钥解密密文, 输出…...

ARCGIS PRO SDK Annotation 概念及操作
使用Annotation的API功能。Annotation 的API功能位于ArcGIS.Core.dll中。Annotation API通常与地理数据库、地图创作和编辑结合使用。ArcGIS.Core.dll ArcGIS.Core.Data.map API中的几乎所有方法都应该在MCT上调用。 一、Annotation featureclass 1、从GeodatabaseGeodatabase数…...
dp专题13 零钱兑换II
本题链接:. - 力扣(LeetCode) 题目: 思路: 根据题意,这是一道很裸的背包问题,其中这里是返回 背包方案数 的。 我们可以直接推出公式 : dp [ j ] dp[ j - coins[ i ] ] 在我之前…...
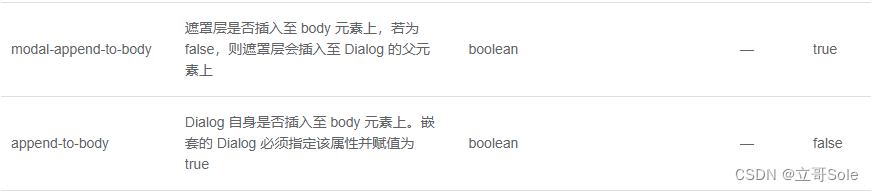
el-dialog嵌套使用,只显示遮罩层的问题
直接上解决方法 <!-- 错误写法 --><el-dialog><el-dialog></el-dialog></el-dialog><!-- 正确写法 --><el-dialog></el-dialog><el-dialog></el-dialog>我是不建议嵌套使用的,平级也能调用,…...
第2版 例3-5 CSS3 动画)
响应式Web开发项目教程(HTML5+CSS3+Bootstrap)第2版 例3-5 CSS3 动画
代码 <!doctype html> <html> <head> <meta charset"utf-8"> <title>CSS3 动画</title> <style> .img {width: 150px; } keyframes rotate { 0% { transform: rotate(0deg); } 100% { transform: rotate(360deg);} } img…...
一款实用的.NET Core加密解密工具类库
前言 在我们日常开发工作中,为了数据安全问题对数据加密、解密是必不可少的。加密方式有很多种如常见的AES,RSA,MD5,SAH1,SAH256,DES等,这时候假如我们有一个封装的对应加密解密工具类可以直接…...

C/C++内存布局
1. C 结构体的内存布局 以一个例子来看struct的内存结构 #define NP_FUNC_WRAPPER __attribute__((optimize(0)))struct StructBody {int first_int_placeholder;int second_int_placeholder;double third_double_placeholder; };class ClassBody {public:int first_int_place…...

springboot(ssm母婴全程服务管理系统 母婴用品服务商城Java系统
springboot(ssm母婴全程服务管理系统 母婴用品服务商城Java系统 开发语言:Java 框架:ssm/springboot vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.7(或8.0…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...
