dp专题13 零钱兑换II
本题链接:. - 力扣(LeetCode)
题目:

思路:
根据题意,这是一道很裸的背包问题,其中这里是返回 背包方案数 的。
我们可以直接推出公式 : dp [ j ] += dp[ j - coins[ i ] ]
在我之前做的笔记中,写过具体的背包方案数dp公式,参考我之前的详解即可:dp专题10 目标和

最后我们再明确一下题目,题目要求是 硬币数量是无限的,说明这是一个 完全背包问题。
完全背包问题 和 01 背包问题区别在于 遍历背包的顺序。
01 背包的 背包 遍历顺序: 逆向。
完全背包的 背包 遍历顺序: 正向。
具体原理是:
背包 逆向 遍历的时候, 物品只能 取 1 次.(01 背包)
代码详解:
for(int i = 0;i < goods.size();++i)
{for(int j = v;j >= goods[i].v;--j){dp[j] = max(dp[j],dp[j - goods.v] + goods.w);}
}/*逆向 的时候, j == 背包容量(v) 时, 只能取当前的一个 物品 i 随后随着 --j 后面 dp[j] 紧随其后 只取一个物品 i 所以达到了,只取 一次 的效果
*/ 背包 正向 遍历的时候, 物品可以取多次.(完全 背包)
代码详解:
for(int i = 0;i < goods.size();++i)
{for(int j = goods[i].v;j <= v;++j){dp[j] = max(dp[j],dp[j - goods.v] + goods.w);}
}/*正向 的时候, j == 物品容量(goods.v) 时, 取当前的一个 物品 i 随后随着 ++j 后面 dp[j] 紧随其后 取一个物品 i 直到达到了 dp[v] ,使得 物品 i 取了多次
*/ 所以 完全背包问题 和 01 背包问题区别在于 遍历背包的顺序。
同样的道理,我们结合dp递推的公式 + 背包遍历顺序,就可以解出这道完全背包问题方案数的问题了。
在这里再扩展一下问题,遍历顺序中,先遍历背包还是先遍历物品?
我们再看一下这两种遍历方法的效果:
①先遍历物品再遍历背包
for(int i = 0;i < goods.size();++i) // 遍历物品
{for(int j = goods[i].v;j <= v;++j) // 遍历背包{dp[j] = max(dp[j],dp[j - goods.v] + goods.w);}
}/*假设 物品 等于 下标那么背包会得到的集合是:{1} {1,2} , {2}{1,2,3} , {2,3} , {3}....获取的集合中不会出现 {2,1}... 等集合说明 先遍历物品再遍历背包是一个 组合 数*/ ②先遍历背包再遍历物品
for(int j = goods[i].v;j <= v;++j) // 遍历背包
{for(int i = 0;i < goods.size();++i) // 遍历物品{dp[j] = max(dp[j],dp[j - goods.v] + goods.w);}
}/*假设 物品 等于 下标那么背包会得到的集合是:{1} {1,2} , {2,1} ,{2}....获取的集合中会出现 {2,1}... 等集合说明 先遍历物品再遍历背包是一个 排列 数*/ 所以 背包问题 遍历顺序中 :
先遍历物品再遍历背包: 组合 数。
先遍历背包再遍历物品: 排列 数。
综上所述。
代码详解如下:
inline int change(int& amount, vector<int>& coins)
{vector<int>dp(amount + 1,0);dp[0] = 1; // dp 初始化 凑成 0 有 1种方法 就是 +0// 组合数遍历for(int &i:coins) // 遍历物品{for(int j = i;j <= amount;++j) // 遍历背包{dp[j] += dp[j - i]; // dp 递推公式}}return dp[amount]; // 返回结果
}最后提交:
相关文章:

dp专题13 零钱兑换II
本题链接:. - 力扣(LeetCode) 题目: 思路: 根据题意,这是一道很裸的背包问题,其中这里是返回 背包方案数 的。 我们可以直接推出公式 : dp [ j ] dp[ j - coins[ i ] ] 在我之前…...
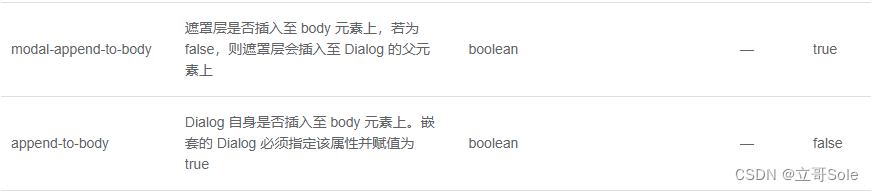
el-dialog嵌套使用,只显示遮罩层的问题
直接上解决方法 <!-- 错误写法 --><el-dialog><el-dialog></el-dialog></el-dialog><!-- 正确写法 --><el-dialog></el-dialog><el-dialog></el-dialog>我是不建议嵌套使用的,平级也能调用,…...
第2版 例3-5 CSS3 动画)
响应式Web开发项目教程(HTML5+CSS3+Bootstrap)第2版 例3-5 CSS3 动画
代码 <!doctype html> <html> <head> <meta charset"utf-8"> <title>CSS3 动画</title> <style> .img {width: 150px; } keyframes rotate { 0% { transform: rotate(0deg); } 100% { transform: rotate(360deg);} } img…...
一款实用的.NET Core加密解密工具类库
前言 在我们日常开发工作中,为了数据安全问题对数据加密、解密是必不可少的。加密方式有很多种如常见的AES,RSA,MD5,SAH1,SAH256,DES等,这时候假如我们有一个封装的对应加密解密工具类可以直接…...

C/C++内存布局
1. C 结构体的内存布局 以一个例子来看struct的内存结构 #define NP_FUNC_WRAPPER __attribute__((optimize(0)))struct StructBody {int first_int_placeholder;int second_int_placeholder;double third_double_placeholder; };class ClassBody {public:int first_int_place…...

springboot(ssm母婴全程服务管理系统 母婴用品服务商城Java系统
springboot(ssm母婴全程服务管理系统 母婴用品服务商城Java系统 开发语言:Java 框架:ssm/springboot vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.7(或8.0…...

修改SSH默认端口,使SSH连接更安全
以CentOS7.9为例: 1、修改配置文件 vi /etc/ssh/sshd_config 2、远程电脑可连接,暂时将SELinux关闭 # 查询状态 getenforce # 关闭 setenforce 0 # 开启 setenforce 1 3、SELinux设置(如果启用),semanage管理工具安…...

React16源码: React中调度之requestWork的源码实现
requestWork 1 )概述 在 scheduleWork 中,找到了创建更新的fiber对应的root节点然后对它进行了一些操作之后,调用了 requestWork,开始请求工作在 requestWork 里面它会做哪些东西呢? 首先我们要把这个root节点加入到调…...

【白话机器学习的数学】读书笔记(3)学习分类(感知机、逻辑回归)
三、学习分类 1.分类的目的 找到一条线把白点和黑点分开。这条直线是使权重向量成为法线向量的直线。(解释见下图) 直线的表达式为: ω ⋅ x ∑ i 1 n ω i ⋅ x i 0 \omegax \sum_{i1}^n\omega_i x_i 0 ω⋅xi1∑nωi⋅xi0 ω \omega ω是权重向量权…...
书生·浦语大模型实战营-学习笔记3
目录 (3)基于 InternLM 和 LangChain 搭建你的知识库1. 大模型开发范式(RAG、Fine-tune)RAG微调 (传统自然语言处理的方法) 2. LangChain简介(RAG开发框架)3. 构建向量数据库4. 搭建知识库助手5. Web Demo部…...
MySQL下对[库]的操作
目录 创建数据库 创建一个数据库案例: 字符集和校验规则: 默认字符集: 默认校验规则: 查看数据库支持的字符集: 查看数据库支持的字符集校验规则: 校验规则对数据库的影响: 操作数据…...
Django(七)
1.靓号管理 1.1 表结构 根据表结构的需求,在models.py中创建类(由类生成数据库中的表)。 class PrettyNum(models.Model):""" 靓号表 """mobile models.CharField(verbose_name"手机号", max_len…...

AT24C02读写操作 一
//AT24C02初始化 void AT24C02_Init(void) { IIC_Init(); } //AT24C02的字节写入 写一个字节 void AT24C02_WordWrite(uint8_Address,uint8_t Data) { //1。主机发送开始信号 IIC_StartSignal(); //2.主机发送器件地址 写操作 IIC_SentBytes(0xA0); //3.主机等侍从机应…...

.NET 8 中引入新的 IHostedLifecycleService 接口 实现定时任务
在这篇文章中,我们将了解 .NET 8 中为托管服务引入的一些新生命周期事件。请注意,这篇文章与 .NET 8 相关,在撰写本文时,.NET 8 目前处于预览状态。在 11 月 .NET 8 最终版本发布之前,类型和实现可能会发生变化。要继续…...

Redis--Geo指令的语法和使用场景举例(附近的人功能)
文章目录 前言Geo介绍Geo指令使用使用场景:附近的人参考文献 前言 Redis除了常见的五种数据类型之外,其实还有一些少见的数据结构,如Geo,HyperLogLog等。虽然它们少见,但是作用却不容小觑。本文将介绍Geo指令的语法和…...

127.0.0.1和0.0.0.0的区别
在网络开发中,经常会涉及到两个特殊的IP地址:127.0.0.1和0.0.0.0。这两者之间有一些关键的区别,本文将深入介绍它们的作用和用途。 127.0.0.1 127.0.0.1 是本地回环地址,通常称为 “localhost”。作用是让网络应用程序能够与本地…...

SpringBoot ES 聚合后多字段加减乘除
SpringBoot ES 聚合后多字段加减乘除 在SpringData Elasticsearch中,聚合统计的原理主要依赖于Elasticsearch本身的聚合框架。Elasticsearch提供了强大的聚合功能,使得你可以对文档进行各种计算和统计,从而得到有关数据集的有用信息。 Elast…...

React16源码: React中requestCurrentTime和expirationTime的源码实现补充
requestCurrentTime 1 )概述 关于 currentTime,在计算 expirationTime 和其他的一些地方都会用到 从它的名义上来讲,应等于performance.now() 或者 Date.now() 就是指定的当前时间在react整体设计当中,它是有一些特定的用处和一些…...

【论文阅读】Deep Graph Contrastive Representation Learning
目录 0、基本信息1、研究动机2、创新点3、方法论3.1、整体框架及算法流程3.2、Corruption函数的具体实现3.2.1、删除边(RE)3.2.2、特征掩盖(MF) 3.3、[编码器](https://blog.csdn.net/qq_44426403/article/details/135443921)的设…...
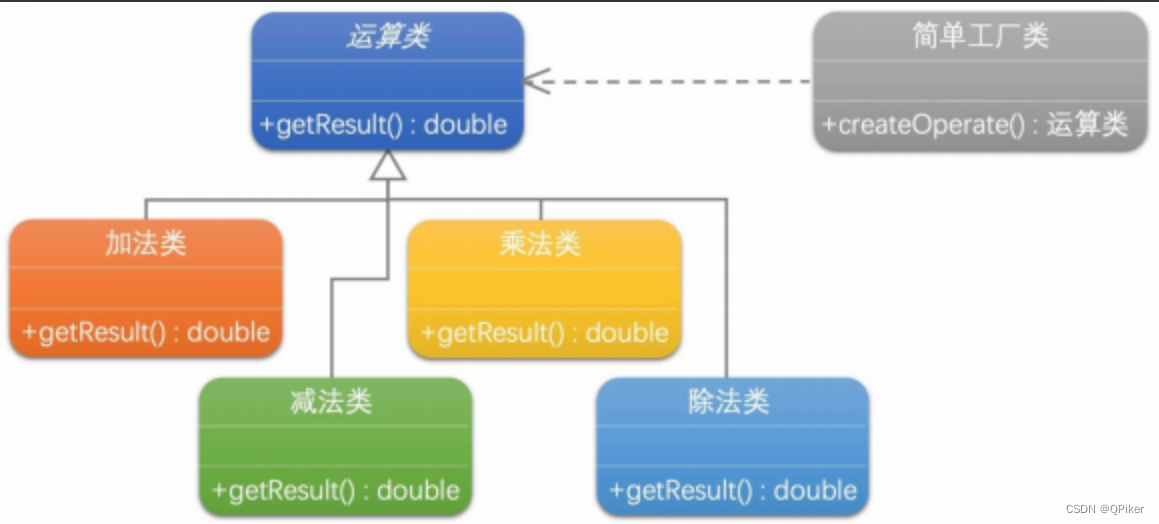
设计模式-简单工厂
设计模式-简单工厂 简单工厂模式是一个集中管理对象创建,并根据条件生成所需类型对象的设计模式,有助于提高代码的复用性和维护性,但可能会导致工厂类过于复杂且违反开闭原则。 抽象提取理论: 封装对象创建过程解耦客户端与产品…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
