【白话机器学习的数学】读书笔记(3)学习分类(感知机、逻辑回归)
三、学习分类
1.分类的目的
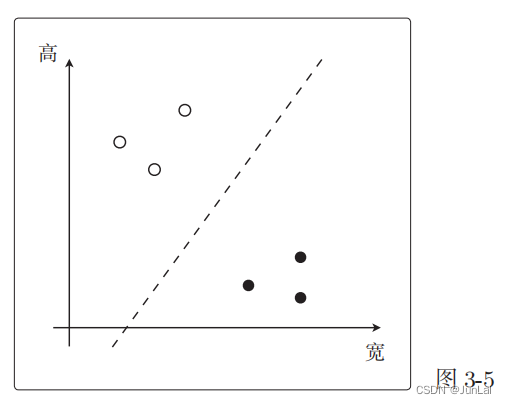
找到一条线把白点和黑点分开。这条直线是使权重向量成为法线向量的直线。(解释见下图)
直线的表达式为:
ω ⋅ x = ∑ i = 1 n ω i ⋅ x i = 0 \omega·x = \sum_{i=1}^n\omega_i · x_i = 0 ω⋅x=i=1∑nωi⋅xi=0
- ω \omega ω是权重向量
- 权重向量就是我们想要知道的未知参数
- 他和回归中的 θ \theta θ是一样的
举个例子:
ω ⋅ x = ( 1 , 1 ) ⋅ ( x 1 , x 2 ) = ω 1 ⋅ x 1 + ω 2 ⋅ x 2 = x 1 + x 2 = 0 \omega·x = (1,1)·(x_1,x_2) = \omega_1·x_1 + \omega_2·x_2 = x_1 + x_2 = 0 ω⋅x=(1,1)⋅(x1,x2)=ω1⋅x1+ω2⋅x2=x1+x2=0
对应的图像:
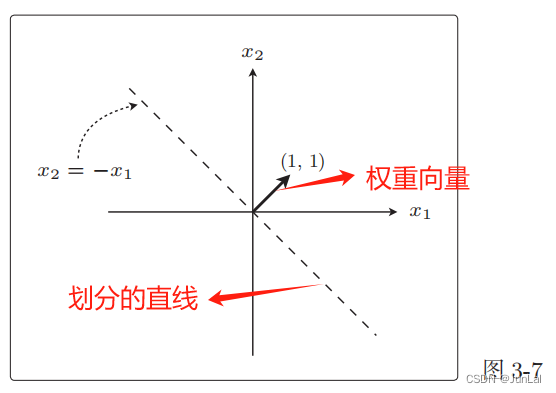
权重向量和这条直线是垂直的。
2.感知机
1定义
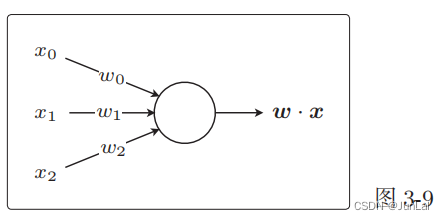
将权重向量用作参数,创建更新表达式来更新参数。基本做法是和回归相同的,感知机是接受多个输入后将每个值与各自的权重相乘,最后输出总和的模型。
感知机的表示:
2判别函数
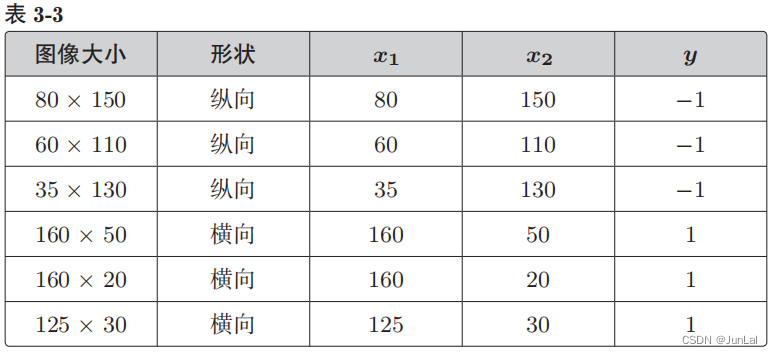
根据参数向量 x 来判断图像是横向还是纵向的函数,即返回 1 或者 −1 的函数 f w ( x ) f_w(x) fw(x)的定义如下。这个函数被称为判别函数。
f ω = { 1 , ( ω ⋅ x ≥ 0 ) − 1 , ( ω ⋅ x < 0 ) f_\omega= \begin{cases}~1,~~~~(\omega·x\ge0) \\-1,~~(\omega·x\lt0)\end{cases} fω={ 1, (ω⋅x≥0)−1, (ω⋅x<0)
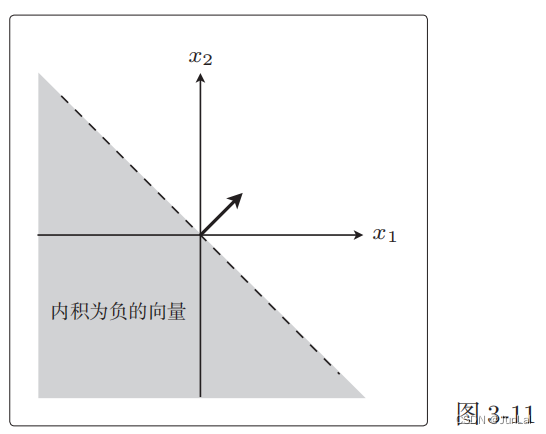
其实, ω ⋅ x \omega · x ω⋅x还可以写成 ω ⋅ x = ∣ ω ∣ ⋅ ∣ x ∣ ⋅ cos θ \omega · x = |\omega| ·| x|·\cos \theta ω⋅x=∣ω∣⋅∣x∣⋅cosθ,那么我们可以推断出 ω ⋅ x \omega · x ω⋅x的正负只跟 θ \theta θ有关系。
向量与权重向量 ω \omega ω之间的夹角为 θ,在 90°<θ< 270° cos θ \cos \theta cosθ为负,所以在 90°<θ< 270°范围内的所有向量都满足内积为负。
3权重向量的更新表达式
ω : = { ω + y ( i ) x ( i ) , f ω ( x ( i ) ) ≠ y ( i ) ω , f ω ( x ( i ) ) = y ( i ) \omega:= \begin{cases} \omega + y^{(i)}x^{(i)},~~~f_\omega(x^{(i)})\ne y^{(i)} \\ \omega,~~~~~~~~~~~~~~~~~~~f_\omega(x^{(i)}) = y^{(i)} \end{cases} ω:={ω+y(i)x(i), fω(x(i))=y(i)ω, fω(x(i))=y(i)
- i指的是训练数据的索引,也就是第i个训练数据的意思
- f ω ( x ( i ) ) = y ( i ) f_\omega(x^{(i)}) = y^{(i)} fω(x(i))=y(i)时说明判别函数的分类结果是准确的,此时不用更新 ω \omega ω
- f ω ( x ( i ) ) ≠ y ( i ) f_\omega(x^{(i)})\ne y^{(i)} fω(x(i))=y(i)时说明判别函数的分类结果不正确,此时需要更新表达式
下面来解释为什么 f ω ( x ( i ) ) ≠ y ( i ) f_\omega(x^{(i)})\ne y^{(i)} fω(x(i))=y(i)时需要更新表达式
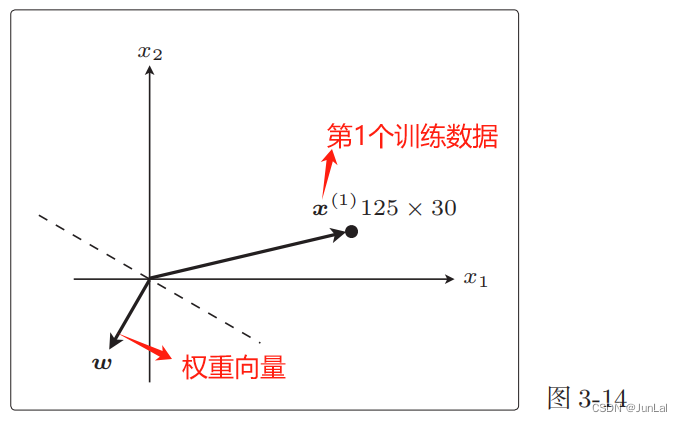
现在权重向量 ω \omega ω 和训练数据的向量 x ( 1 ) x^{(1)} x(1)二者的方向几乎相反, ω \omega ω和 x ( 1 ) x^{(1)} x(1)之间的夹角 θ 的范围是 90◦ <θ< 270◦ ,内积为负。
也就是说,判别函数 f ω ( x ( 1 ) ) f_\omega(x^{(1)}) fω(x(1))的结果为 −1。

f ω ( x ( 1 ) ) ≠ y ( 1 ) f_\omega(x^{(1)}) \ne y^{(1)} fω(x(1))=y(1),说明分类失败。
更新: 由于 y ( 1 ) = 1 ,故 ω + y ( 1 ) x ( 1 ) = ω + x ( 1 ) 由于y^{(1)} = 1,故\omega + y^{(1)}x^{(1)} = \omega + x^{(1)} 由于y(1)=1,故ω+y(1)x(1)=ω+x(1)
图像的变化更明显一些:
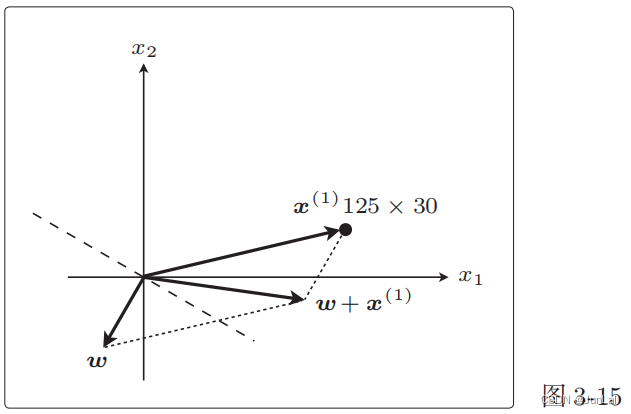
这个 ω + x ( 1 ) \omega + x^{(1)} ω+x(1)就是下一个新的 ω \omega ω,相当于把原来的线旋转了一下。
刚才处理的是标签值 y = 1 的情况,而对于 y = −1 的情况,只是更新表达式的向量加法变成了减法。本质的做法都是在分类
失败时更新权重向量,使得直线旋转相应的角度。这样重复更新所有的参数,就是感知机的学习方法。
4感知机的缺点
只能解决线性可分的问题。线性可分指的就是能够使用直线分类的情况。
之前提到的感知机也被称为简单感知机或单层感知机,是很弱的模型。既然有单层感知机,那么就会有多层感知机。实际上多层感知机就是神经网络。
3.逻辑回归
与感知机的不同之处在于,它是把分类作为概率来考虑的,举个例子,x是横向的概率是80%,而感知机的结果是A是横向。然后判别函数的两个值设置为0和1。
f ω = { 1 , ( ω ⋅ x ≥ 0 ) 0 , ( ω ⋅ x < 0 ) f_\omega= \begin{cases}1,~~~(\omega·x\ge0) \\0,~~~(\omega·x\lt0)\end{cases} fω={1, (ω⋅x≥0)0, (ω⋅x<0)
1 Sigmoid函数
能够将未知数据分类为某个类别的函数 f θ ( x ) f_\theta(x) fθ(x) ,类似感知机的判别函数 f ω ( x ) f_\omega(x) fω(x),在这里我们把 f θ ( x ) f_\theta(x) fθ(x)当作概率,对应的前面举的横向的例子。 f θ ( x ) = 80 % f_\theta(x) = 80\% fθ(x)=80% 表示的就是x是横向图像的概率是80%。
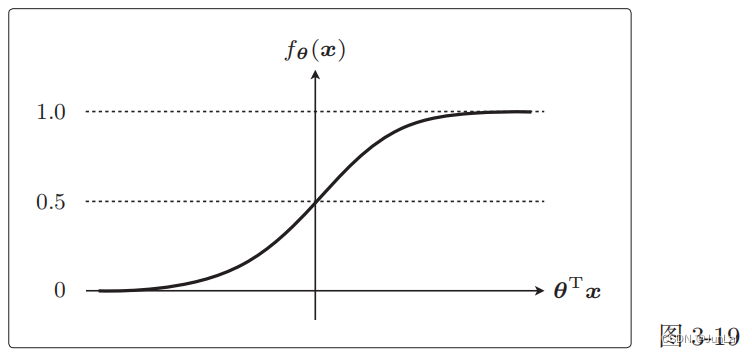
f θ ( x ) = 1 1 + e ( − θ T x ) f_\theta(x) = \frac{1}{1+e^{(-\theta^Tx)}} fθ(x)=1+e(−θTx)1
函数图像
两个特征
- θ T x = 0 \theta^Tx = 0 θTx=0时, f θ ( x ) = 0.5 f_\theta(x) = 0.5 fθ(x)=0.5
- 0 < f θ ( x ) ≤ 1 0\lt f_\theta(x)\le1 0<fθ(x)≤1
2 决策边界
把 f θ ( x ) f_\theta(x) fθ(x)当作概率,我们还可以有另一种等价的表达式
f θ ( x ) = P ( y = 1 ∣ x ) f_\theta(x) = P(y=1|x) fθ(x)=P(y=1∣x)
P ( y = 1 ∣ x ) P(y=1|x) P(y=1∣x)表示给出x数据时y=1的概率。
假如 f θ ( x ) = 0.7 f_\theta(x) = 0.7 fθ(x)=0.7,我们会把x分类为横向。 f θ ( x ) = 0.2 f_\theta(x) = 0.2 fθ(x)=0.2,横向的概率为20%,纵向的概率为80%,这种状态可以分类为纵向。这里我们就是以0.5为阈值,然后把$f_\theta(x) $的结果与其比较,从而得到分类的结果。
即你的分类表达式为:
y = { 1 , ( f θ ( x ) ≥ 0.5 ) 0 , ( f θ ( x ) < 0.5 ) y= \begin{cases}1,~~~(f_\theta(x)\ge0.5) \\0,~~~(f_\theta(x)\lt0.5)\end{cases} y={1, (fθ(x)≥0.5)0, (fθ(x)<0.5)
从图像中可以看出 f θ ( x ) ≥ 0.5 f_\theta(x) \ge 0.5 fθ(x)≥0.5时, θ T x ≥ 0 \theta^Tx\ge0 θTx≥0,反之。
所以分类表达式可以写成:
y = { 1 , ( θ T x ≥ 0 ) 0 , ( θ T x < 0 ) y= \begin{cases}1,~~~(\theta^Tx\ge0) \\0,~~~(\theta^Tx\lt0)\end{cases} y={1, (θTx≥0)0, (θTx<0)
假设有一个训练数据为
θ = [ θ 0 θ 1 θ 2 ] = [ − 100 2 1 ] , x = [ 1 x 1 x 2 ] (2) \theta = \begin{bmatrix} \theta_0\\ \theta_1\\ \theta_2\\ \end{bmatrix} \tag{2} = \begin{bmatrix} -100\\2\\1 \end{bmatrix} , x = \begin{bmatrix} 1\\x_1\\x_2 \end{bmatrix} θ= θ0θ1θ2 = −10021 ,x= 1x1x2 (2)
所以
θ T x = − 100 ⋅ 1 + 2 x 1 + x 2 ≥ 0 → x 2 ≥ − 2 x 2 + 100 \theta^Tx = -100\cdot1+2x_1+x_2\ge0 \to x_2\ge -2x_2+100 θTx=−100⋅1+2x1+x2≥0→x2≥−2x2+100
对应的图像为
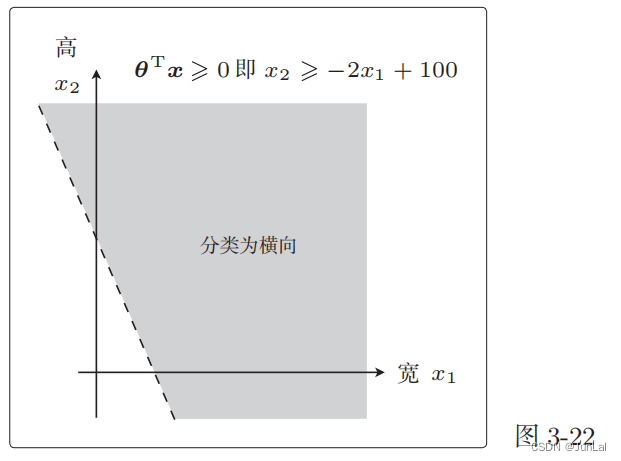
将 θ T x = 0 \theta^Tx = 0 θTx=0 这条直线作为边界线,就可以把这条线两侧的数据分类为横向和纵向。
这样用于数据分类的直线称为决策边界。
然后的做法和回归一样,为了求得正确的参数 θ 而定义目标函数,进行微分,然后求出参数的更新表达式。
4.似然函数(解决逻辑回归中参数更新表达式问题)
P(y = 1|x) 是图像为横向的概率,P(y = 0|x) 是图像为纵向的概率
- y = 1 的时候,我们希望概率 P(y = 1|x) 是最大的
- y = 0 的时候,我们希望概率 P(y = 0|x) 是最大的
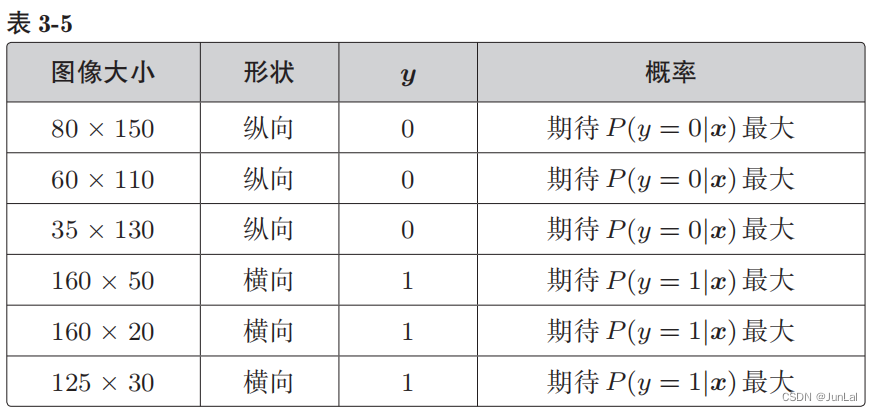
假定所有的训练数据都是互不影响、独立发生的,这种情况下整体的概率就可以用下面的联合概率来表示
L ( θ ) = P ( y ( 1 ) = 0 ∣ x ( 1 ) ) P ( y ( 2 ) = 0 ∣ x ( 2 ) ) ⋅ ⋅ ⋅ P ( y ( 6 ) = 1 ∣ x ( 6 ) ) L(θ) = P(y^{(1)} = 0 | x^{(1)})P(y^{(2)} = 0 | x^{(2)})··· P(y^{(6)} = 1 | x^{(6)}) L(θ)=P(y(1)=0∣x(1))P(y(2)=0∣x(2))⋅⋅⋅P(y(6)=1∣x(6))
将联合概率一般化:
L ( θ ) = ∏ i = 1 n P ( y ( i ) = 1 ∣ x ( i ) ) y ( i ) P ( y ( i ) = 0 ∣ x ( i ) ) 1 − y ( i ) L(θ) =\prod_{i=1}^n P(y^{(i)} = 1 | x^{(i)})^{y^{(i)}} P(y^{(i)} = 0 | x^{(i)})^{1−y^{(i)}} L(θ)=i=1∏nP(y(i)=1∣x(i))y(i)P(y(i)=0∣x(i))1−y(i)
回归的时候处理的是误差,所以要最小化,而现在考虑的是联合概率,我们希望概率尽可能大,所以要最大化。这里的目标函数 L ( θ ) L(\theta) L(θ)也被称为似然,L就是Likelihood。
我们可以认为似然函数 L(θ) 中,使其值最大的参数 θ 能够最近似地说明训练数据。
1.对数似然函数
直接对似然函数进行微分有点困难,在此之前要把函数变形。取似然函数的对数,在等式两边加上 log:
log L ( θ ) = log ∏ i = 1 n P ( y ( i ) = 1 ∣ x ( i ) ) y ( i ) P ( y ( i ) = 0 ∣ x ( i ) ) 1 − y ( i ) \log L(θ) = \log \prod_{i=1}^n P(y^{(i)} = 1 | x^{(i)})^{y^{(i)}} P(y^{(i)} = 0 | x^{(i)})^{1−y^{(i)}} logL(θ)=logi=1∏nP(y(i)=1∣x(i))y(i)P(y(i)=0∣x(i))1−y(i)
然后进行变形:
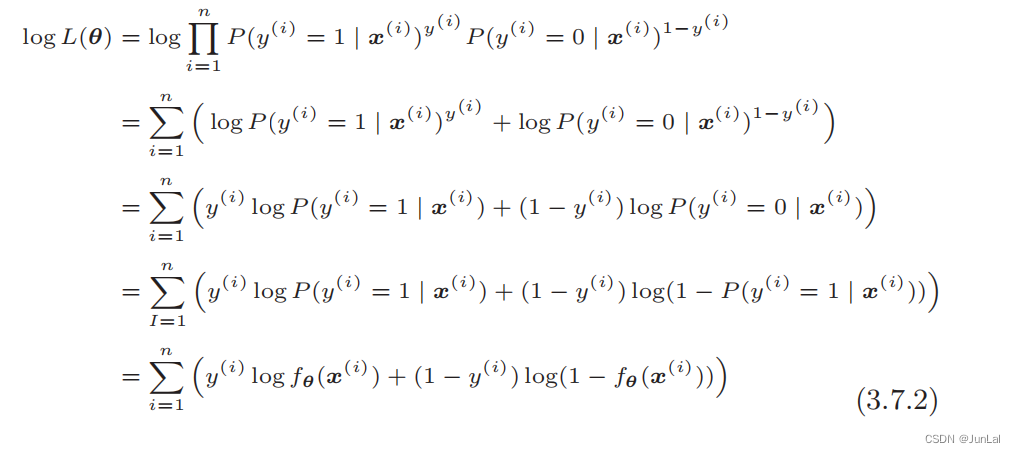
最终得到:
log L ( θ ) = ∑ i = 1 n [ y ( i ) log f θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − f θ ( x ( i ) ) ) ] \log L(θ) = \sum_{i=1}^n \bigg [y^{(i)}\log f_\theta(x^{(i)})+ (1−y^{(i)})\log (1 - f_\theta(x^{(i)})~)\bigg] logL(θ)=i=1∑n[y(i)logfθ(x(i))+(1−y(i))log(1−fθ(x(i)) )]
2.似然函数的微分
逻辑回归就是要将这个对数似然函数用作目标函数:
log L ( θ ) = ∑ i = 1 n [ y ( i ) log f θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − f θ ( x ( i ) ) ) ] \log L(θ) = \sum_{i=1}^n \bigg [y^{(i)}\log f_\theta(x^{(i)})+ (1−y^{(i)})\log (1 - f_\theta(x^{(i)})~)\bigg] logL(θ)=i=1∑n[y(i)logfθ(x(i))+(1−y(i))log(1−fθ(x(i)) )]
接下来对每个参数 θ j \theta_j θj求微分:
∂ log L ( θ ) ∂ θ j = ∂ ∂ θ j ∑ i = 1 n [ y ( i ) log f θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − f θ ( x ( i ) ) ) ] \frac{\partial \log L(θ)}{\partial \theta_j} = \frac{\partial}{\partial \theta_j}\sum_{i=1}^n \bigg [y^{(i)}\log f_\theta(x^{(i)})+ (1−y^{(i)})\log (1 - f_\theta(x^{(i)})~)\bigg] ∂θj∂logL(θ)=∂θj∂i=1∑n[y(i)logfθ(x(i))+(1−y(i))log(1−fθ(x(i)) )]
接下来的求解步骤和回归的也差不多:
1.改写成复合函数求微分
u = log L ( θ ) v = f θ ( x ) ∂ u ∂ θ j = ∂ u ∂ v ⋅ ∂ v ∂ θ j u = \log L(\theta)\\ v = f_\theta(x)\\ \frac{\partial u}{\partial \theta_j} = \frac{\partial u}{\partial v} \cdot \frac{\partial v}{\partial \theta_j} u=logL(θ)v=fθ(x)∂θj∂u=∂v∂u⋅∂θj∂v
2.计算第一项 ∂ u ∂ v \frac{\partial u}{\partial v} ∂v∂u
∂ u ∂ v = ∂ ∂ θ j ∑ i = 1 n [ y ( i ) log ( v ) + ( 1 − y ( i ) ) log ( 1 − v ) ] d log ( v ) d v = 1 v , d log ( 1 − v ) d v = − 1 1 − v ∂ u ∂ v = ∑ i = 1 n ( y ( i ) v − 1 − y ( i ) 1 − v ) \frac{\partial u}{\partial v} = \frac{\partial}{\partial \theta_j}\sum_{i=1}^n \bigg [y^{(i)}\log(v)+ (1−y^{(i)})\log (1 - v)\bigg]\\ \frac{d\log(v)}{dv} = \frac{1}{v} , ~~\frac{d\log(1-v)}{dv} = -\frac{1}{1-v}\\ \frac{\partial u}{\partial v} = \sum_{i=1}^n(\frac{y^{(i)}}{v} - \frac{1−y^{(i)}}{1-v}) ∂v∂u=∂θj∂i=1∑n[y(i)log(v)+(1−y(i))log(1−v)]dvdlog(v)=v1, dvdlog(1−v)=−1−v1∂v∂u=i=1∑n(vy(i)−1−v1−y(i))
3.计算第二项 ∂ v ∂ θ j \frac{\partial v}{\partial \theta_j} ∂θj∂v
∂ v ∂ θ j = ∂ ∂ θ j 1 1 + e − θ T x z = θ T x v = f θ ( x ) = 1 1 + e − z ∂ v ∂ θ j = ∂ v ∂ z ⋅ ∂ z ∂ θ j \frac{\partial v}{\partial \theta_j }= \frac{\partial }{\partial \theta_j }\frac{1}{1+e^{-\theta^Tx}}\\ z = θ^Tx\\ v = f_θ(x) = \frac{1}{1 + e^{−z}}\\ \frac{\partial v}{\partial \theta_j} = \frac{\partial v}{\partial z} \cdot \frac{\partial z}{\partial \theta_j} ∂θj∂v=∂θj∂1+e−θTx1z=θTxv=fθ(x)=1+e−z1∂θj∂v=∂z∂v⋅∂θj∂z
其中(过程可以手推一次):
∂ v ∂ z = v ( 1 − v ) ∂ z ∂ θ j = x j \frac{\partial v}{\partial z} = v(1-v)\\ \frac{\partial z}{\partial \theta_j} = x_j\\ ∂z∂v=v(1−v)∂θj∂z=xj
所以:
∂ v ∂ θ j = v ( 1 − v ) ⋅ x j \frac{\partial v}{\partial \theta_j} =v(1-v)\cdot x_j ∂θj∂v=v(1−v)⋅xj
4.整合
∂ u ∂ θ j = ∂ u ∂ v ⋅ ∂ v ∂ θ j = ∑ i = 1 n ( y ( i ) v − 1 − y ( i ) 1 − v ) ⋅ v ( 1 − v ) ⋅ x j ( i ) = ∑ i = 1 n ( y ( i ) ( 1 − v ) − ( 1 − y ( i ) ) v ) x j ( i ) = ∑ i = 1 n ( y ( i ) − y ( i ) v − v + y ( i ) v ) x j ( i ) = ∑ i = 1 n ( y ( i ) − v ) x j ( i ) = ∑ i = 1 n ( y ( i ) − f θ ( x ( i ) ) ) x j ( i ) \begin{aligned} \frac{\partial u}{\partial \theta_j} &= \frac{\partial u}{\partial v} \cdot \frac{\partial v}{\partial \theta_j} \\ &=\sum_{i=1}^n(\frac{y^{(i)}}{v} - \frac{1−y^{(i)}}{1-v})\cdot v(1-v)\cdot x_j^{(i)}\\ &=\sum_{i=1}^n\bigg(y^{(i)}(1-v) - (1−y^{(i)})v\bigg) x_j^{(i)}\\ &=\sum_{i=1}^n\bigg(y^{(i)} - y^{(i)}v - v + y^{(i)}v\bigg) x_j^{(i)}\\ &=\sum_{i=1}^n\bigg(y^{(i)} - v\bigg) x_j^{(i)}\\ &=\sum_{i=1}^n\bigg(y^{(i)} - f_θ(x^{(i)})\bigg) x_j^{(i)}\\ \end{aligned} ∂θj∂u=∂v∂u⋅∂θj∂v=i=1∑n(vy(i)−1−v1−y(i))⋅v(1−v)⋅xj(i)=i=1∑n(y(i)(1−v)−(1−y(i))v)xj(i)=i=1∑n(y(i)−y(i)v−v+y(i)v)xj(i)=i=1∑n(y(i)−v)xj(i)=i=1∑n(y(i)−fθ(x(i)))xj(i)
3.得到参数更新表达式
现在是以最大化为目标,所以必须按照与最小化时相反的方向移动参数,所以更新表达式中变成了+:
θ j : = θ j + η ∑ i = 1 n ( y ( i ) − f θ ( x ( i ) ) ) x j ( i ) \theta_j := \theta_j + \eta\sum_{i=1}^n\bigg(y^{(i)} - f_θ(x^{(i)})\bigg) x_j^{(i)} θj:=θj+ηi=1∑n(y(i)−fθ(x(i)))xj(i)
当然也可以为了和回归的式子保持一致,这样的话 η \eta η后面括号里面的式子就要变号了:
θ j : = θ j − η ∑ i = 1 n ( f θ ( x ( i ) − y ( i ) ) ) x j ( i ) \theta_j := \theta_j - \eta\sum_{i=1}^n\bigg(f_θ(x^{(i)} - y^{(i)})\bigg) x_j^{(i)} θj:=θj−ηi=1∑n(fθ(x(i)−y(i)))xj(i)
5.线性不可分
类似下图这样的,就是线性不可分:
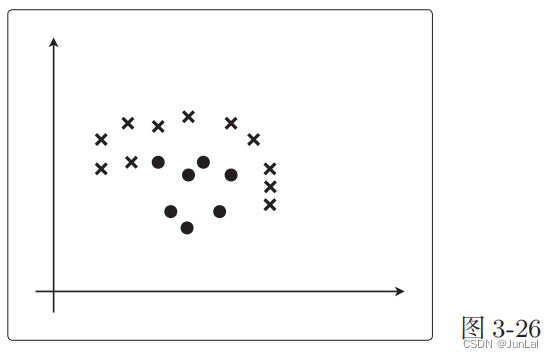
直线不能分类,但曲线是可以将其分类的。所以我们可以像学习多项式回归那样去增加次数。即:
θ = [ θ 0 θ 1 θ 2 θ 3 ] , x = [ 1 x 1 x 2 x 1 2 ] (2) \theta = \begin{bmatrix} \theta_0\\ \theta_1\\ \theta_2\\ \theta_3\\ \end{bmatrix} \tag{2} , x = \begin{bmatrix} 1\\x_1\\x_2\\x_1^2 \end{bmatrix} θ= θ0θ1θ2θ3 ,x= 1x1x2x12 (2)
所以:
θ T x = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 2 \theta^Tx = \theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_1^2 θTx=θ0+θ1x1+θ2x2+θ3x12
举个例子:
θ = [ θ 0 θ 1 θ 2 θ 3 ] = [ 0 0 1 − 1 ] (2) \theta = \begin{bmatrix} \theta_0\\ \theta_1\\ \theta_2\\ \theta_3\\ \end{bmatrix} \tag{2} = \begin{bmatrix} 0\\ 0\\ 1\\ -1\\ \end{bmatrix} θ= θ0θ1θ2θ3 = 001−1 (2)
所以:
θ T x = x 2 − x 1 2 ≥ 0 \theta^Tx = x_2 - x_1^2 \ge 0 θTx=x2−x12≥0
对应的图像:

根据图像我们也可以看出。前面的决策边界是直线,现在是曲线。这也就是逻辑回归应用于线性不可分问题的方法。
通过随意地增加次数,就可以得到复杂形状的决策边界。
同样,在逻辑回归的参数更新中也可以使用随机梯度下降法。
相关文章:

【白话机器学习的数学】读书笔记(3)学习分类(感知机、逻辑回归)
三、学习分类 1.分类的目的 找到一条线把白点和黑点分开。这条直线是使权重向量成为法线向量的直线。(解释见下图) 直线的表达式为: ω ⋅ x ∑ i 1 n ω i ⋅ x i 0 \omegax \sum_{i1}^n\omega_i x_i 0 ω⋅xi1∑nωi⋅xi0 ω \omega ω是权重向量权…...
书生·浦语大模型实战营-学习笔记3
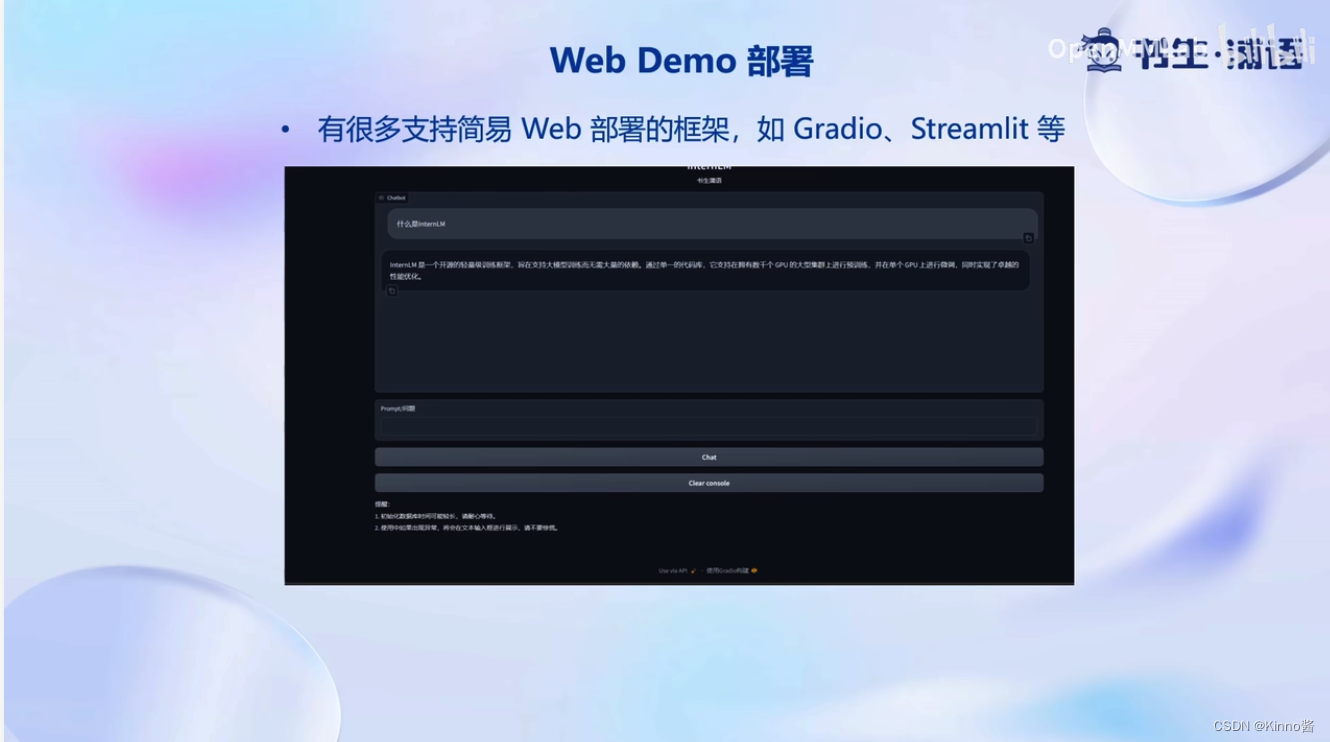
目录 (3)基于 InternLM 和 LangChain 搭建你的知识库1. 大模型开发范式(RAG、Fine-tune)RAG微调 (传统自然语言处理的方法) 2. LangChain简介(RAG开发框架)3. 构建向量数据库4. 搭建知识库助手5. Web Demo部…...
MySQL下对[库]的操作
目录 创建数据库 创建一个数据库案例: 字符集和校验规则: 默认字符集: 默认校验规则: 查看数据库支持的字符集: 查看数据库支持的字符集校验规则: 校验规则对数据库的影响: 操作数据…...
Django(七)
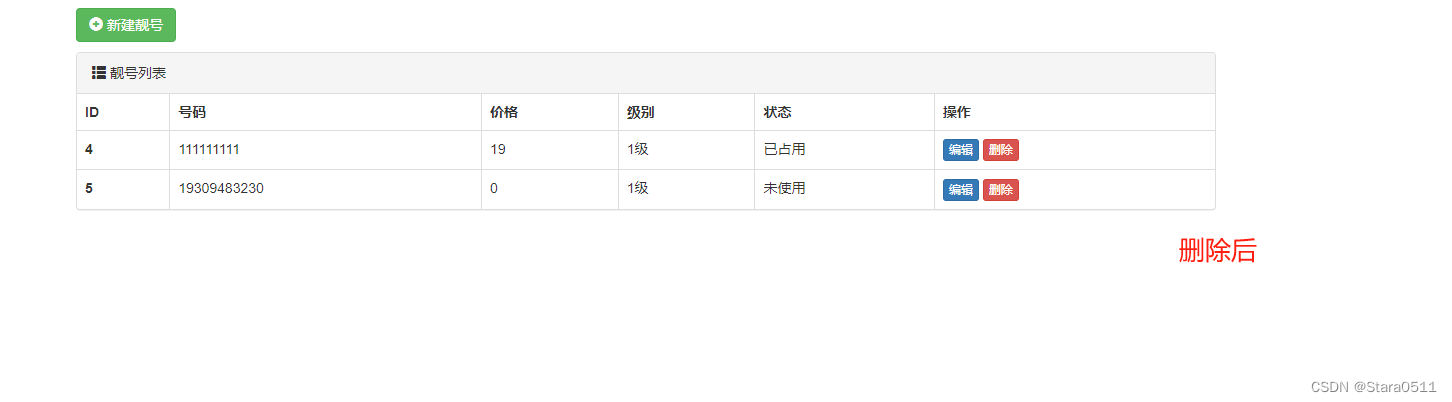
1.靓号管理 1.1 表结构 根据表结构的需求,在models.py中创建类(由类生成数据库中的表)。 class PrettyNum(models.Model):""" 靓号表 """mobile models.CharField(verbose_name"手机号", max_len…...

AT24C02读写操作 一
//AT24C02初始化 void AT24C02_Init(void) { IIC_Init(); } //AT24C02的字节写入 写一个字节 void AT24C02_WordWrite(uint8_Address,uint8_t Data) { //1。主机发送开始信号 IIC_StartSignal(); //2.主机发送器件地址 写操作 IIC_SentBytes(0xA0); //3.主机等侍从机应…...

.NET 8 中引入新的 IHostedLifecycleService 接口 实现定时任务
在这篇文章中,我们将了解 .NET 8 中为托管服务引入的一些新生命周期事件。请注意,这篇文章与 .NET 8 相关,在撰写本文时,.NET 8 目前处于预览状态。在 11 月 .NET 8 最终版本发布之前,类型和实现可能会发生变化。要继续…...

Redis--Geo指令的语法和使用场景举例(附近的人功能)
文章目录 前言Geo介绍Geo指令使用使用场景:附近的人参考文献 前言 Redis除了常见的五种数据类型之外,其实还有一些少见的数据结构,如Geo,HyperLogLog等。虽然它们少见,但是作用却不容小觑。本文将介绍Geo指令的语法和…...

127.0.0.1和0.0.0.0的区别
在网络开发中,经常会涉及到两个特殊的IP地址:127.0.0.1和0.0.0.0。这两者之间有一些关键的区别,本文将深入介绍它们的作用和用途。 127.0.0.1 127.0.0.1 是本地回环地址,通常称为 “localhost”。作用是让网络应用程序能够与本地…...

SpringBoot ES 聚合后多字段加减乘除
SpringBoot ES 聚合后多字段加减乘除 在SpringData Elasticsearch中,聚合统计的原理主要依赖于Elasticsearch本身的聚合框架。Elasticsearch提供了强大的聚合功能,使得你可以对文档进行各种计算和统计,从而得到有关数据集的有用信息。 Elast…...

React16源码: React中requestCurrentTime和expirationTime的源码实现补充
requestCurrentTime 1 )概述 关于 currentTime,在计算 expirationTime 和其他的一些地方都会用到 从它的名义上来讲,应等于performance.now() 或者 Date.now() 就是指定的当前时间在react整体设计当中,它是有一些特定的用处和一些…...

【论文阅读】Deep Graph Contrastive Representation Learning
目录 0、基本信息1、研究动机2、创新点3、方法论3.1、整体框架及算法流程3.2、Corruption函数的具体实现3.2.1、删除边(RE)3.2.2、特征掩盖(MF) 3.3、[编码器](https://blog.csdn.net/qq_44426403/article/details/135443921)的设…...
设计模式-简单工厂
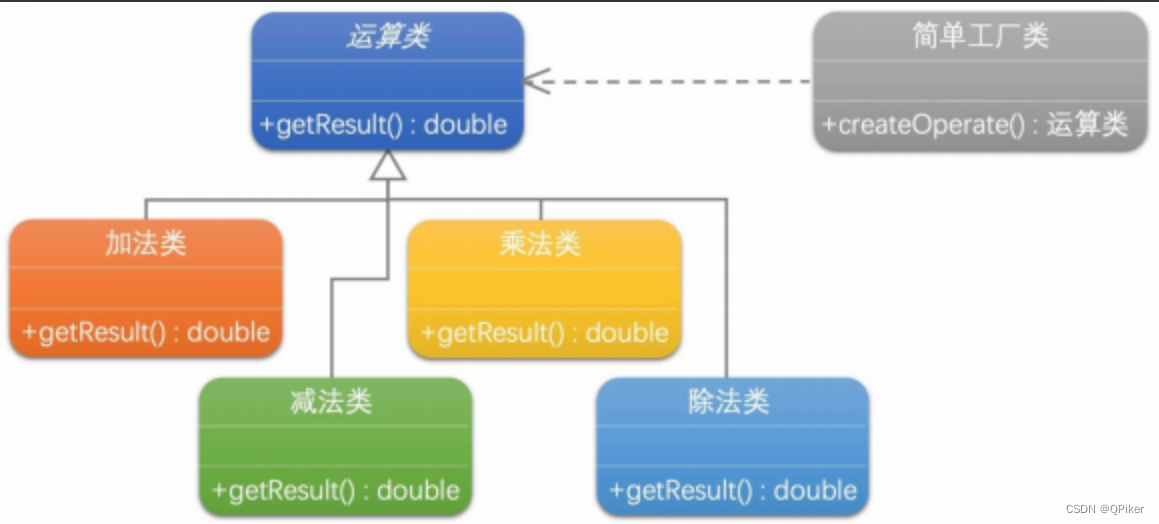
设计模式-简单工厂 简单工厂模式是一个集中管理对象创建,并根据条件生成所需类型对象的设计模式,有助于提高代码的复用性和维护性,但可能会导致工厂类过于复杂且违反开闭原则。 抽象提取理论: 封装对象创建过程解耦客户端与产品…...
)
Django ORM 中的单表查询 API(1)
在 Django 中,对象关系映射(ORM)提供了一种功能强大、表现力丰富的数据库交互方式。ORM 允许开发人员使用高级 Python 代码执行数据库查询,从而更轻松地处理数据库实体。 下面,我们将探讨 Django ORM 中单表查询 API …...
电子雨html代码
废话不多说下面是代码: <!DOCTYPE html><html lang"en"><head><meta charset"UTF-8"><title>Code</title><style>body{margin: 0;overflow: hidden;}</style></head><body><c…...

xadmin基于Django的后台管理系统安装与使用
xadmin是基于Django的后台管理系统 官网:http://sshwsfc.github.io/xadmin/ github地址:https://github.com/sshwsfc/xadmin 安装方式 pip安装 pip install xadmin在setting配置中添加: INSTALLED_APPS [xadmin,crispy_forms, ]在urls.py…...

[go语言]输入输出
目录 知识结构 输入 1.Scan 编辑 2.Scanf 3.Scanln 4.os.Stdin --标准输入,从键盘输入 输出 1.Print 2.Printf 3.Println 知识结构 输入 为了展示集中输入的区别,将直接进行代码演示。 三者区别的结论:Scanf格式化输入&#x…...

【SpringBoot系列】AOP详解
🤵♂️ 个人主页:@香菜的个人主页,加 ischongxin ,备注csdn ✍🏻作者简介:csdn 认证博客专家,游戏开发领域优质创作者,华为云享专家,2021年度华为云年度十佳博主 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞👍🏻 收…...

openssl3.2 - 官方demo学习 - signature - rsa_pss_hash.c
文章目录 openssl3.2 - 官方demo学习 - signature - rsa_pss_hash.c概述笔记END openssl3.2 - 官方demo学习 - signature - rsa_pss_hash.c 概述 对私钥对明文做签名(摘要算法为SHA256) 用公钥对密文做验签(摘要算法为SHA256) 笔记 /*! \file rsa_pss_hash.c \note openss…...

Redis相关知识点
1.什么是Redis Redis (REmote DIctionary Server) 是用 C 语言开发的一个开源的高性能键值对(key-value)数据库,它支持网络,可基于内存亦可持久化,并提供多种语言的API。Redis具有高效性、原子性、支持多种数据结构、…...
嵌入式开发--STM32G4系列片上FLASH的读写
这个玩意吧,说起来很简单,就是几行代码的事,但楞是折腾了我大半天时间才搞定。原因后面说,先看代码吧: 读操作 读操作很简单,以32位方式读取的时候是这样的: data *(__IO uint32_t *)(0x080…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
