当前位置： 首页 > news >正文

深度学习记录--梯度检验

news 2026/2/10 1:29:04

数值逼近

为了对梯度进行检验，需要计算近似误差值来接近梯度

对于单边误差和双边误差公式，其中双边误差与真实梯度相差更小，故一般采用双边误差公式

双边误差

公式：g(\theta )=\frac{f(\theta+\varepsilon)-f(\theta-\varepsilon )}{2\varepsilon}

梯度检验(gradient checking)

对于成本函数，求出\theta^{[i]}的导数，计算出双边误差d\Theta^{[i]}=\frac{J(\theta1,\theta2,...,\theta i+\varepsilon,...)-J(\theta1,\theta2,...,\theta i-\varepsilon,...)}{2\varepsilon}，再将两者进行比较

比较方法：

s=\left \| d\Theta_{approx}-d\Theta \right \|_{2}，判断s的大小

若s<10^{-7}，则误差很小，效果很好

若s<10^{-5}，则误差一般，效果一般

若s<10^{-3}，则误差较大，需要考虑是否错误较多


梯度检验的注意事项

不要在训练中使用梯度检验，它只适用于调试

梯度检验的计算时间较长，且通常在backprop后向传播中进行

当梯度检验得出偏差过大时，要对所有参数进行检查

使用正则化时，要记住在梯度检验中保留正则项

不要在梯度检验的过程中使用dropout

在每次迭代过程中，dropout会随机消除隐层单元的不同子集，J函数难以明确计算

相关文章：

深度学习记录--梯度检验

数值逼近 为了对梯度进行检验&#xff0c;需要计算近似误差值来接近梯度 对于单边误差和双边误差公式&#xff0c;其中双边误差与真实梯度相差更小&#xff0c;故一般采用双边误差公式 双边误差 公式&#xff1a; 梯度检验(gradient checking) 对于成本函数&#xff0c;求出…...

编程日记 2024/1/18 14:20:14

ERP进出库+办公用品管理系统

系统架构 简介系统架构部分页面结构图UML逻辑图办公用品入出库 简介 本系统适用于ERP企业公司职员关于系统化的申请相关办公用品&#xff0c;提高整体系统整合行&#xff0c;加大上下级之间的联系&#xff0c;规避因人员过多&#xff0c;而浪费人力在简单重复的工作中&#xf…...

编程日记 2024/1/18 14:17:11

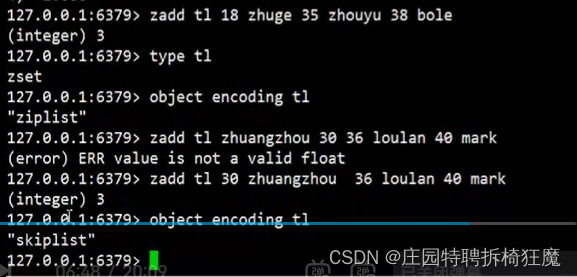
Redis 笔记一

概览 1.Redis核心数据存储结构 2.Redis底层String编码int&embstr&raw 3.Redis底层压缩列表&跳表&哈希表 4.Redis底层Zset实现压缩列表和跳表如何选择 5.基于Redis实现微博&抢红包&12306核心业务 辅助学习&#xff1a;Redis 教程 | 菜鸟教程 1.Redis为什…...

编程日记 2024/1/18 14:16:10

学习记录687@spring data jpa 动态传递list参数并判断list是否为空

实际应用中需要在spring data jpa中使用原生sql&#xff0c;传递的参数是list&#xff0c;要根据list判断是否为空来判断是否要使用这个参数。 尝试了很多方法&#xff0c;比如size、length、is null、!null等等&#xff0c;都要报错&#xff0c;比如could not extract Result…...

编程日记 2024/1/18 14:13:08

寒假刷题第五天

PTA甲级 1022 Digital Library 大模拟 #include<iostream> #include<unordered_map> #include<unordered_set> #include<vector> #include<set>using namespace std;unordered_map<string , set<int>>ti , au , key , pub , year…...

编程日记 2024/1/18 14:12:06

Leetcode454四数相加Ⅱ（java实现）

今天&#xff0c;我们分享的题目是Leetcode454四数相加Ⅱ&#xff0c;我们先来看题目&#xff1a; 首先可以从题意中大体得知&#xff0c;也是从某个集合中找有没有符合条件的元素。遇见这种类型的题目我们可以考虑用哈希表&#xff0c;本题我们选取的是map集合&#xff0c;因…...

编程日记 2024/1/18 14:10:02

mysql 容器化安装（docker）离线和在线

前言&#xff1a;在部署hive或airflow 升级过程中&#xff0c;总需要一个对应的数据库存储元数据&#xff0c;一个轻量级的mysql容器刚刚好。轻量、可快速移植、具有隔离性。 文章目录 1、查看机器版本2、安装 docker3、启动docker 服务4、docker 常用命令docker5、拉取mysql …...

编程日记 2024/1/18 14:09:01

2. FPGA的电路结构概述

文章目录 1. 引言2. FPGA的一般结构2.1 概要2.2 FPGA三部分构成间的关系&#xff1a; 3. 小结 1. 引言 结构决定原理。原理未必决定结构。理解FPGA结构&#xff0c;进而能阐明其工作原理很有必要。FPGA产品的风云变换&#xff0c;其基本结构保持相对不变。 2. FPGA的一般结构…...

编程日记 2024/1/18 14:04:57

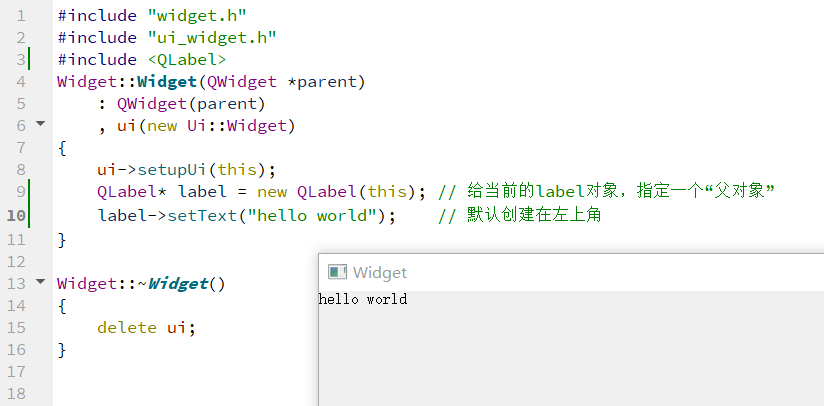
【Qt】Qt配置

需要云服务器等云产品来学习Linux的同学可以移步/-->腾讯云<--/-->阿里云<--/-->华为云<--/官网&#xff0c;轻量型云服务器低至112元/年&#xff0c;新用户首次下单享超低折扣。 目录 一、Qt SDK下载 二、配置环境变量 三、新建工程(QWidget) 四、QWidg…...

编程日记 2024/1/18 14:01:54

查看Linux系统内存、CPU、磁盘使用率和详细信息

一、查看内存占用 1、free # free -m 以MB为单位显示内存使用情况 [rootlocalhost ~]# free -mtotal used free shared buff/cache available Mem: 11852 1250 8668 410 1934 9873 Swap: 601…...

编程日记 2024/1/18 13:54:48

HttpServletRequest getServerPort()、getLocalPort() 、getRemotePort() 区别

getRemotePort() 、getServerPort()、getLocalPort() request.getServerPort()、request.getLocalPort() 和 request.getRemotePort() 这三个方法都是获取与HTTP请求相关的端口信息的 客户端(如浏览器)通过某个随机分配的网络连接端口(7070) 向服务器发送HTTP请求( http://exam…...

编程日记 2024/1/18 13:53:46

NVIDIA jetson编译opencv 源码 python版本

安装 jetson-stats 查看GPU的利用率 sudo apt-get install python3-pip sudo -H pip3 install jetson-stats 运行 jtop 进行查看 opencv 编译python版本 编译命令 cmake -D CMAKE_INSTALL_PREFIX/usr/local/opencv-4.6.0 -D CMAKE_BUILD_TYPERELEASE -D WITH_OPENGLON -D …...

编程日记 2024/1/18 13:52:45

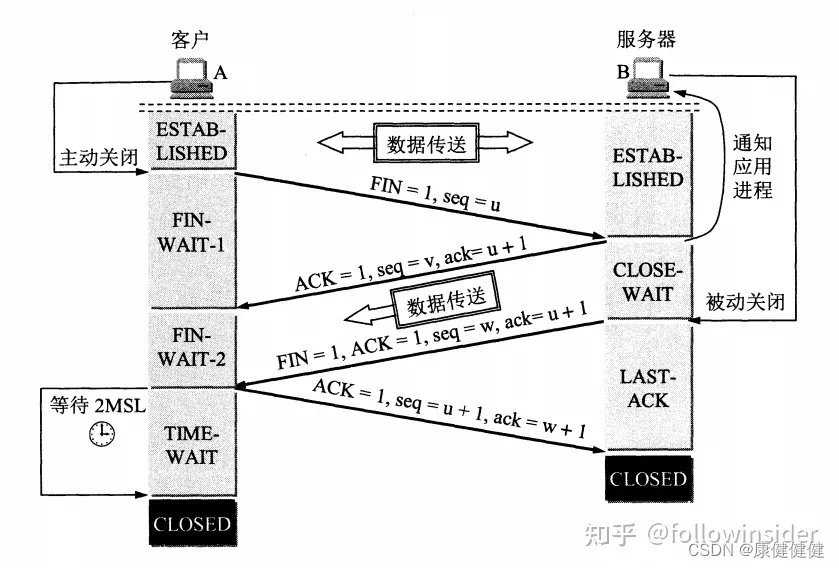
TCP的三次握手，四次挥手

三次握手 第一次握手&#xff1a;客户端发送SYN报文&#xff0c;井发送seq为x序列号给服务端&#xff0c;等待服务端的确认第二次握手&#xff1a;服务端发送SYNACK报文&#xff0c;并发送seq为Y的序列号&#xff0c;在确认序列号为x1第三次握手&#xff1a;客户端发送ACK报文&…...

编程日记 2024/1/18 13:51:44

ElasticSearch高阶使用

目录 一、match_all 二、 text和keyword的区别 三、match、term的区别 四、exists query 五、 ids query 六、range query范围查询 七、prefix query前缀查询 八、 wildcard query通配符查询 九、 fuzzy query模糊查询 十、match query匹配查询 十一、multi_match q…...

编程日记 2024/1/18 13:50:44

美易官方：盘前：道指期货跌0.4% “恐怖数据”将发布

盘前&#xff1a;道指期货跌0.4% “恐怖数据”将发布 在今日的盘前交易中&#xff0c;道琼斯工业平均指数期货小幅下跌0.4%&#xff0c;市场正在等待即将发布的“恐怖数据”——美国零售销售数据。这一数据被视为衡量美国经济健康状况的重要指标&#xff0c;因此备受关注。 由于…...

编程日记 2024/1/18 13:47:41

appium之联动pycharm

前置条件&#xff1a; 1.java环境安装好了 2.android-sdk安装好&#xff08;uiautomatorviewer 也可以把这个启动起来&#xff09; 3.appium安装好 4.adb devices查看下设备是否连接 pycharm入门代码--固定写法 from appium import webdriver# 定义字典变量 desired_caps …...

编程日记 2024/1/18 13:46:40

Java中泛型的详细介绍

引言&#xff1a; Java语言中的泛型是一种强大的特性&#xff0c;它允许我们在编写代码时指定类、接口和方法的参数类型。通过使用泛型&#xff0c;我们可以提高代码的重用性、可读性和安全性。在本博客中&#xff0c;我们将详细介绍Java中泛型的知识。 一、泛型的基本概念 泛型…...

编程日记 2024/1/18 13:42:37

chrome 307状态码

问题&#xff1a;不知道什么原因导致http请求chrome始终307跳转到https,这个307的跳转非常恶心的地方是客户端缓存行为&#xff0c;并且非普通的f12下面清除缓存可以去掉 解决办法&#xff1a;使用chrome的清除浏览数据&#xff0c;通过这个方式清除&#xff0c;才能解决。 问…...

编程日记 2024/1/18 13:41:36

Redis在Windows10中安装和配置

1.首先去下载Redis 这里不给出下载地址&#xff0c;自己可以用去搜索一下地址 下载 下载完成后解压到D盘redis下&#xff0c;本人用的是3.2.100 D:\Redis\Redis-x64-3.2.100 2.解压完成后需要设置环境变量&#xff0c;这里新建一个系统环境变量中path 中添加一个文件所…...

编程日记 2024/1/18 13:39:34

华为OD机试 - 特殊的加密算法（Java JS Python C）

题目描述 有一种特殊的加密算法，明文为一段数字串，经过密码本查找转换，生成另一段密文数字串。 规则如下： 明文为一段数字串由 0~9 组成密码本为数字 0~9 组成的二维数组需要按明文串的数字顺序在密码本里找到同样的数字串，密码本里的数字串是由相邻的单元格数字组成，上…...

编程日记 2024/1/18 13:33:28

谷歌浏览器插件

项目中有时候会用到插件 sync-cookie-extension1.0.0&#xff1a;开发环境同步测试 cookie 至 localhost&#xff0c;便于本地请求服务携带 cookie 参考地址&#xff1a;https://juejin.cn/post/7139354571712757767 里面有源码下载下来&#xff0c;加在到扩展即可使用FeHelp…...

编程新知 2025/8/16 3:55:30

地震勘探——干扰波识别、井中地震时距曲线特点

目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波&#xff1a;可以用来解决所提出的地质任务的波&#xff1b;干扰波&#xff1a;所有妨碍辨认、追踪有效波的其他波。 地震勘探中&#xff0c;有效波和干扰波是相对的。例如&#xff0c;在反射波…...

编程新知 2026/2/8 20:43:05

LeetCode - 394. 字符串解码

题目 394. 字符串解码 - 力扣&#xff08;LeetCode&#xff09; 思路 使用两个栈&#xff1a;一个存储重复次数&#xff0c;一个存储字符串 遍历输入字符串&#xff1a; 数字处理&#xff1a;遇到数字时&#xff0c;累积计算重复次数左括号处理&#xff1a;保存当前状态&a…...

编程新知 2026/1/25 10:09:59

OkHttp 中实现断点续传 demo

在 OkHttp 中实现断点续传主要通过以下步骤完成&#xff0c;核心是利用 HTTP 协议的 Range 请求头指定下载范围&#xff1a; 实现原理 Range 请求头&#xff1a;向服务器请求文件的特定字节范围&#xff08;如 Range: bytes1024-&#xff09; 本地文件记录&#xff1a;保存已…...

编程新知 2025/12/12 0:56:22

srs linux

下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935&#xff0c;SRS管理页面端口是8080&#xff0c;可…...

编程新知 2026/2/6 9:49:55

如何将联系人从 iPhone 转移到 Android

从 iPhone 换到 Android 手机时&#xff0c;你可能需要保留重要的数据&#xff0c;例如通讯录。好在&#xff0c;将通讯录从 iPhone 转移到 Android 手机非常简单&#xff0c;你可以从本文中学习 6 种可靠的方法&#xff0c;确保随时保持连接&#xff0c;不错过任何信息。 第 1…...

编程新知 2026/1/31 5:09:27

【Oracle】分区表

个人主页&#xff1a;Guiat 归属专栏&#xff1a;Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

编程新知 2026/1/20 21:59:36

Linux --进程控制

本文从以下五个方面来初步认识进程控制&#xff1a; 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程&#xff0c;创建出来的进程就是子进程&#xff0c;原来的进程为父进程。…...

编程新知 2026/1/30 15:27:25

Java求职者面试指南：Spring、Spring Boot、MyBatis框架与计算机基础问题解析

Java求职者面试指南&#xff1a;Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问&#xff08;基础概念问题&#xff09; 1. 请解释Spring框架的核心容器是什么&#xff1f;它在Spring中起到什么作用&#xff1f; Spring框架的核心容器是IoC容器&#…...

编程新知 2025/10/4 21:24:40

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案

这个问题我看其他博主也写了&#xff0c;要么要会员、要么写的乱七八糟。这里我整理一下&#xff0c;把问题说清楚并且给出代码&#xff0c;拿去用就行&#xff0c;照着葫芦画瓢。 问题 在继承QWebEngineView后&#xff0c;重写mousePressEvent或event函数无法捕获鼠标按下事…...

编程新知 2025/6/11 3:07:32