【信号与系统】【北京航空航天大学】实验三、连续时间信号的频域分析 【MATLAB】
一、实验目的
1、掌握 傅立叶变换(The Fourier Transform) 及其性质;
2、掌握连续时间信号傅立叶变换的数值计算方法;
3、掌握利用 MATLAB 实现信号的幅度调制(Amplitude Modulation, AM) 的方法;
4、掌握利用 MATLAB 实现对周期信号的频谱分析。
二、实验内容
1、
MATLAB代码:
>> clear all;
>> t = -4 : 0.001 : 4;
>> N = input('N = ');
N = 3
>> c0 = 0.5;
>> fN = c0 * ones(1, length(t));
>> for n = 1 : 2 : N
fN = fN + cos(n * pi * t / 2) * sinc(n / 2);
end
>> figure
>> plot(t, fN);
>> title(['N = ' num2str(N)]);
>> xlabel('t');
>> ylabel('f(t)');
>> figure
>> fN = c0 * ones(1, length(t));
>> N = input('N = ');
N = 9
>> for n = 1 : 2 : N
fN = fN + cos(n * pi * t / 2) * sinc(n / 2);
end
>> plot(t, fN);
>> title(['N = ' num2str(N)]);
>> xlabel('t');
>> ylabel('f(t)');
>> figure
>> fN = c0 * ones(1, length(t));
>> N = input('N = ');
N = 24
>> for n = 1 : 2 : N
fN = fN + cos(n * pi * t / 2) * sinc(n / 2);
end
>> plot(t, fN);
>> title(['N = ' num2str(N)]);
>> xlabel('t');
>> ylabel('f(t)');
>> figure
>> fN = c0 * ones(1, length(t));
>> N = input('N = ');
N = 70
>> for n = 1 : 2 : N
fN = fN + cos(n * pi * t / 2) * sinc(n / 2);
end
>> plot(t, fN);
>> title(['N = ' num2str(N)]);
>> xlabel('t');
>> ylabel('f(t)');
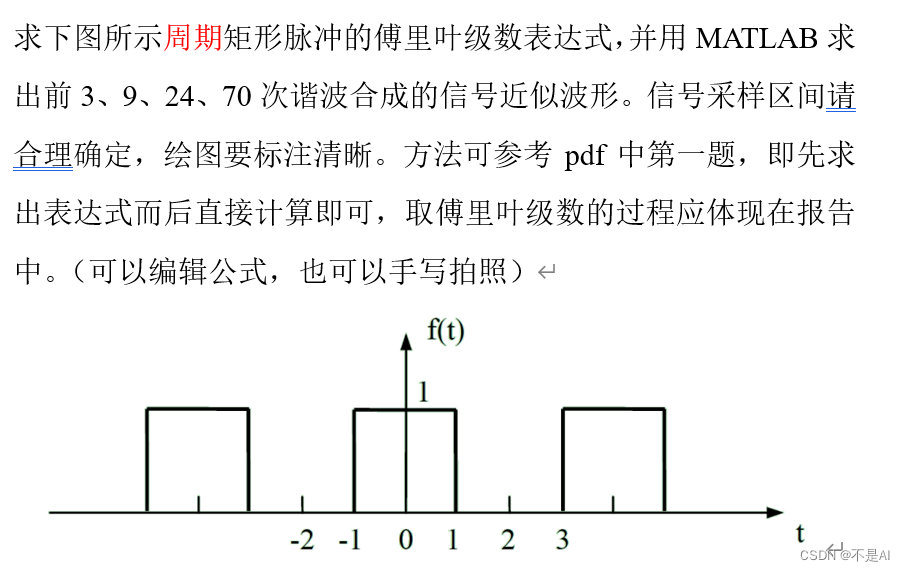
公式推导:
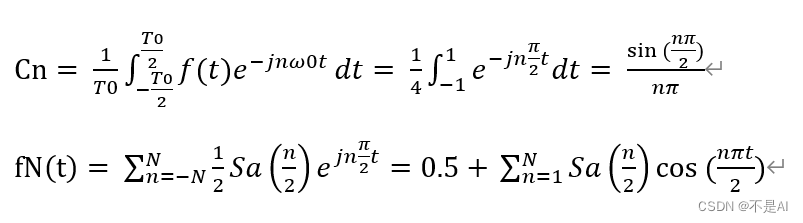
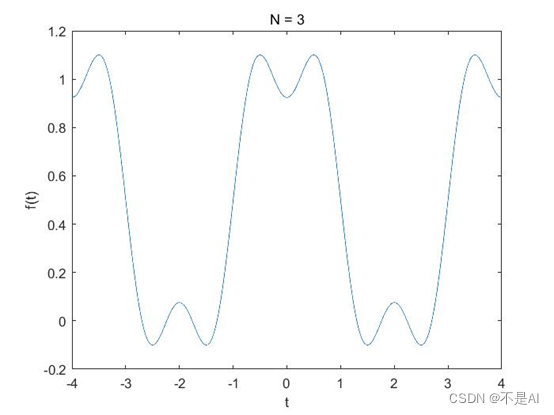
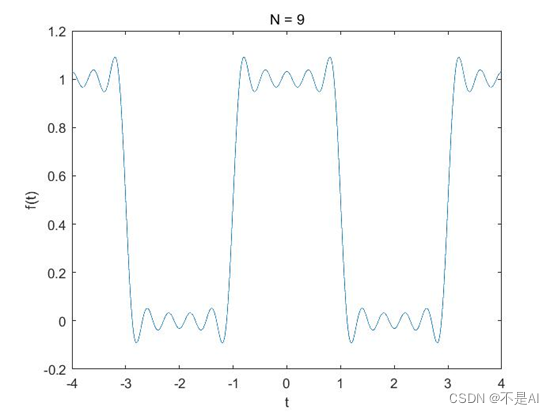
叠加生成的信号波形图:
(1)N = 3:
(2)N = 9:
(3)N = 24:
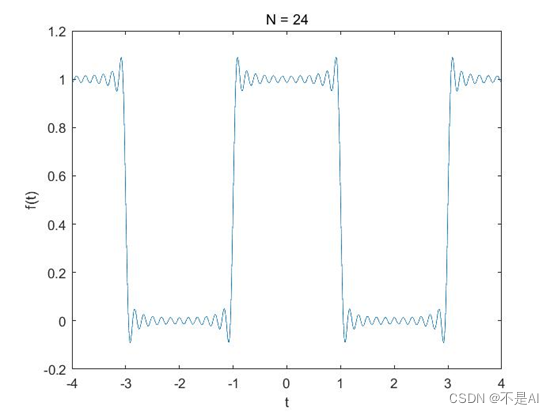
(4)N = 70:
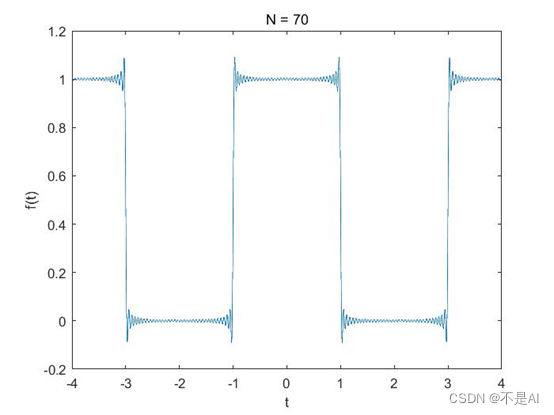
2、

MATLAB代码:
(1)、绘制方波信号:
>> clear all;
>> t = -6 : 0.001 : 6;
>> n = round(length(t) / 12);
>> f = [-2 * ones(n, 1); 2 * ones(2 * n, 1); -2 * ones(2 * n, 1); 2 * ones(2 * n, 1);-2 * ones(2 * n, 1); 2 * ones(2 * n, 1); -2 * ones(n + 1, 1)];
>> figure
>> plot(t, f);
>> axis([-6 6 -3 3]);
>> grid on;
>> title('方波信号', 'FontSize', 14);
>> xlabel('t');
>> ylabel('f(t)');
(2)、进行谐波叠加:
>> clear all;
>> t = -4 : 0.001 : 4;
>> fN = 0;
>> N = 2;
>> for n = 1 : N
fN = fN + 4 * (sinc(n / 2) - sinc(n)) * cos(n * pi / 2 * t);
end
>> m = round(length(t) / 8);
>> figure
>> subplot(2, 2, 1);
>> f = [2 * ones(m, 1); -2 * ones(2 * m, 1); 2 * ones(2 * m, 1); -2 * ones(2 * m, 1); 2 * ones(m + 1, 1)];
>> plot(t, f);
>> grid on;
>> axis([-4 4 -3 3]);
>> hold on;
>> plot(t, fN);
>> title('1~2次谐波叠加', 'FontSize', 14);
>> xlabel('t');
>> ylabel('f(t)');
>> subplot(2, 2, 2);
>> fN = 0;
>> N = 4;
>> for n = 1 : N
fN = fN + 4 * (sinc(n / 2) - sinc(n)) * cos(n * pi / 2 * t);
end
>> plot(t, f);
>> grid on;
>> axis([-4 4 -3 3]);
>> hold on;
>> plot(t, fN);
>> title('1~4次谐波叠加', 'FontSize', 14);
>> xlabel('t');
>> ylabel('f(t)');
>> subplot(2, 2, 3);
>> fN = 0;
>> N = 6;
>> for n = 1 : N
fN = fN + 4 * (sinc(n / 2) - sinc(n)) * cos(n * pi / 2 * t);
end
>> plot(t, f);
>> grid on;
>> axis([-4 4 -3 3]);
>> hold on;
>> plot(t, fN);
>> title('1~6次谐波叠加', 'FontSize', 14);
>> xlabel('t');
>> ylabel('f(t)');
>> subplot(2, 2, 4);
>> fN = 0;
>> N = 100;
>> for n = 1 : N
fN = fN + 4 * (sinc(n / 2) - sinc(n)) * cos(n * pi / 2 * t);
end
>> plot(t, f);
>> grid on;
>> axis([-4 4 -3 3]);
>> hold on;
>> plot(t, fN);
>> title('1~100次谐波叠加', 'FontSize', 14);
>> xlabel('t');
>> ylabel('f(t)');
生成的信号波形图:
(1)、方波信号:
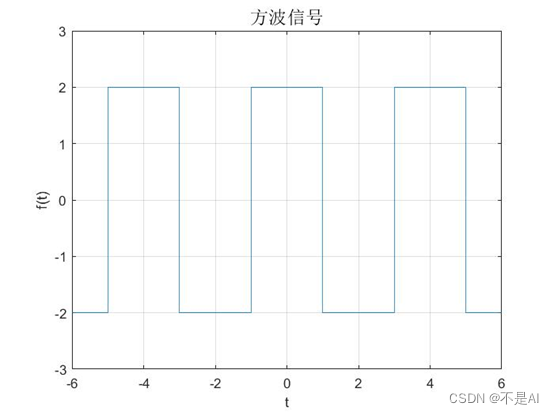
(2)、谐波叠加结果:
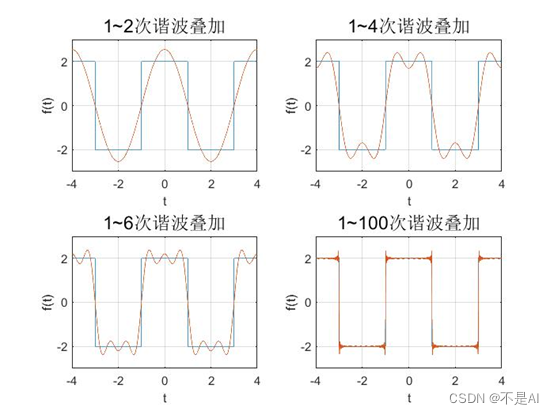
3、

求傅里叶级数过程:

MATLAB代码:
>> clear all;
>> N = 10;
>> n1 = -N : -1;
>> C1 = 4 * j * sin(n1 * pi / 2) / pi ^ 2 ./ n1 .^ 2;
>> C0 = 0;
>> n2 = 1 : N;
>> C2 = 4 * j * sin(n2 * pi / 2) / pi ^ 2 ./ n2 .^ 2;
>> Cn = [C1, C0, C2];
>> n = -N : N;
>> figure
>> subplot(2, 1, 1);
>> stem(n, abs(Cn));
>> axis([-10 10 0 0.5]);
>> grid on;
>> ylabel('Cn的幅度谱');
>> subplot(2, 1, 2);
>> stem(n, angle(Cn));
>> grid on;
>> ylabel('Cn的相位谱');
>> xlabel('\omega/\omega_0');
生成的幅度谱和相位谱:
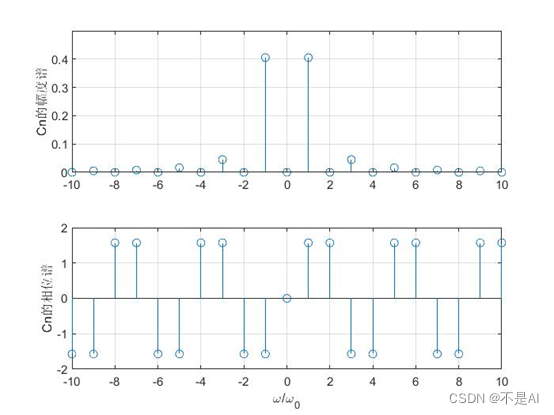
4、

求傅里叶级数过程:
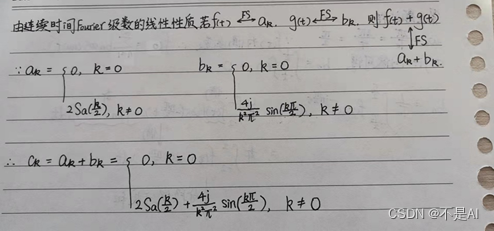
MATLAB代码:
>> clear all;
>> n1 = -10 : -1;
>> n2 = 1 : 10;
>> C1 = 2 * sinc(n1 / 2) + 4 * j * sin(n1 * pi / 2) / pi ^ 2 ./ n1 .^ 2;
>> C2 = 2 * sinc(n2 / 2) + 4 * j * sin(n2 * pi / 2) / pi ^ 2 ./ n2 .^ 2;
>> C0 = 0;
>> n = -10 : 10;
>> Cn = [C1, C0, C2];
>> figure
>> subplot(2, 1, 1);
>> stem(n, abs(Cn));
>> grid on;
>> ylabel('Cn的幅度谱');
>> subplot(2, 1, 2);
>> stem(n, angle(Cn));
>> grid on;
>> ylabel('Cn的相位谱');
>> xlabel('\omega/\omega_0');
生成的幅度谱和相位谱:
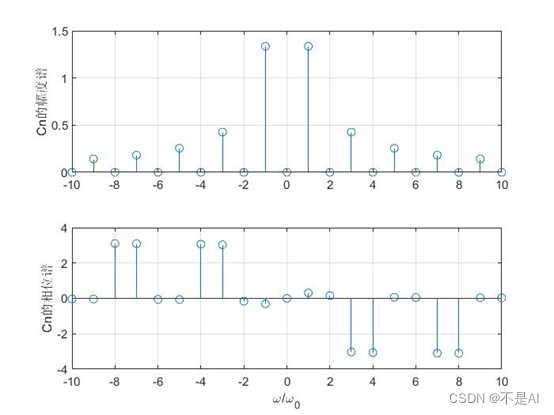
5、思考题
第2题中所提及的不同的产生方波信号的方法,分别有什么优点与缺点?
答:
用本题中的方法产生方波信号的缺点是较为复杂,需要将一个周期分割成若干部分,并对每一部分分别赋值;优点是免去了占空比的计算,且信号不一定以y = 0为中心上下振动;用square函数产生方波信号的优点是函数调用较为简单;缺点是需要先已知或通过计算得出信号的占空比,且只能绘制关于x轴上下对称(以y=0为中心振动)的方波信号。
三、实验收获与感想:
1、 遇到新的函数,可以在命令行中输入 “help + 函数名”命令来了解此函数的用法;
2、 sinc函数的两种定义:

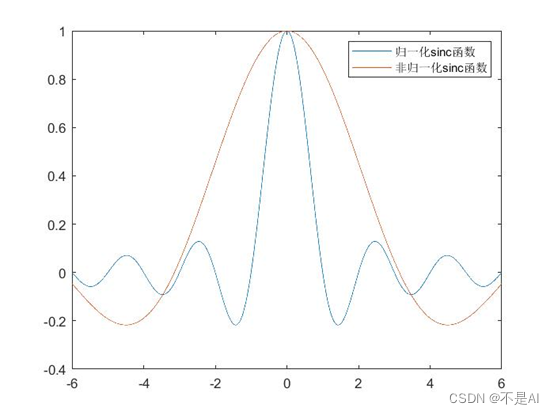
MATLAB R2020a中的sinc函数是归一化的sinc函数。
3、 绘制方波时最好在一张图上绘制2~3个周期;
4、 函数用法:ones(n, 1); num2str( ); title函数的格式化用法; abs(Z); angle(Z);
三、参考书目
《信号与系统(第二版)》,【美】Alan V. Oppenheim 等 著,刘树棠 译,北京,电子工业出版社,2020年8月。
相关文章:

【信号与系统】【北京航空航天大学】实验三、连续时间信号的频域分析 【MATLAB】
一、实验目的 1、掌握 傅立叶变换(The Fourier Transform) 及其性质; 2、掌握连续时间信号傅立叶变换的数值计算方法; 3、掌握利用 MATLAB 实现信号的幅度调制(Amplitude Modulation, AM) 的方法ÿ…...
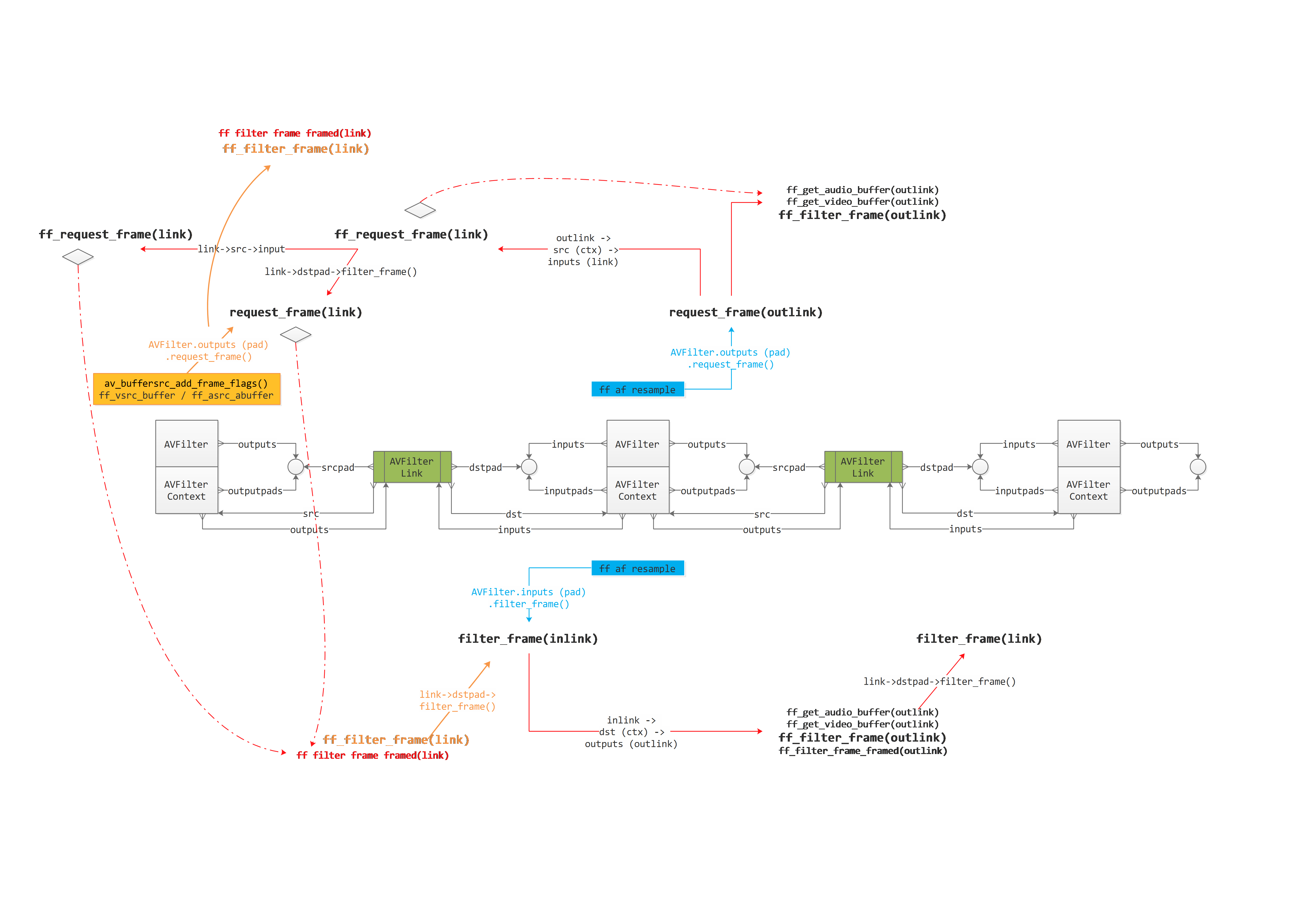
FFmpeg之AVFilter
文章目录 一、概述二、重要结构体2.1、AVFilterGraph2.2、AVFilter2.3、AVFilterContext 三、流程梳理3.1、FFmpeg AVFilter 使用整体流程3.2、过滤器构建流程3.2.1、分配AVFilterGraph3.2.2、创建过滤器源3.2.3、创建接收过滤器3.2.4、生成源和接收过滤器的输入输出3.2.5、通过…...
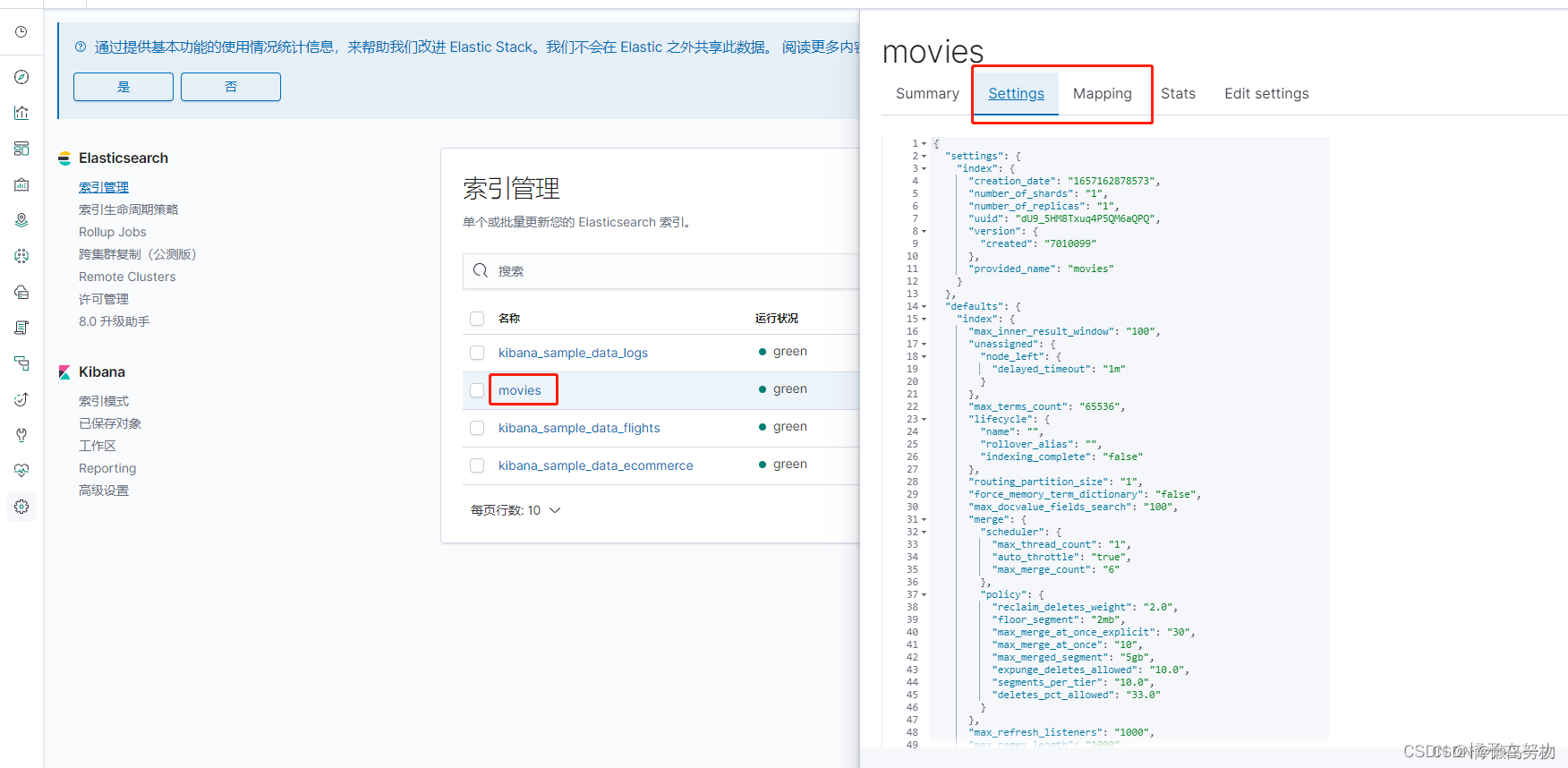
ES 之索引和文档
本文主要介绍ES中的数据组成结构单元。 一、文档(Document) 1、概念 ES的数据存储单元是面向文档的,文档是所有数据存储,搜索的最小单元。 你可以把ES中的文档对应成mysql中的一条条数据记录。到时候你存进ES的数据就是一个个文档。 文档存入ES是序列…...
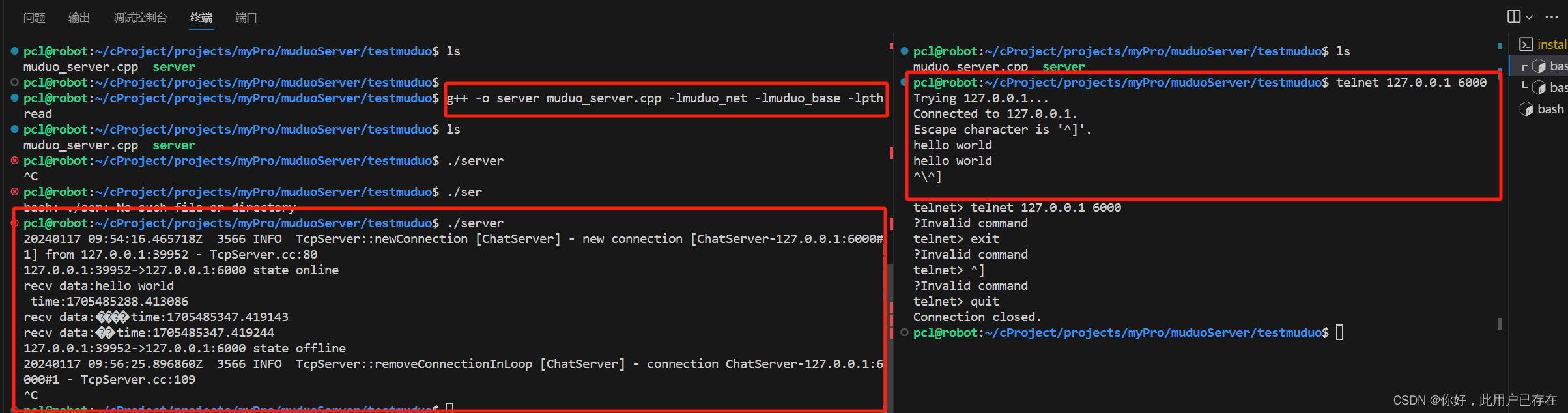
使用muduo库编写网络server端
muduo库源码编译安装和环境搭建 C muduo网络库知识分享01 - Linux平台下muduo网络库源码编译安装-CSDN博客 #include<iostream> #include<muduo/net/TcpServer.h> #include<muduo/net/EventLoop.h> using namespace std; using namespace muduo; using name…...

Unity3D和three.js的比较
一、Unity3D和three.js简介 Unity3D是一款跨平台的游戏引擎,可以用于开发2D和3D游戏。它提供了一个可视化的开发环境,包含了强大的编辑器和工具,使开发者可以方便地创建游戏场景、添加物体、设置物理效果、编写脚本等。Unity3D支持多种平台,包括PC、移动设备、主机等,可以…...

JavaScript 类型判断及类型转换规则
文章目录 JavaScript 类型及其判断使用 typeof 判断类型使用 instanceof 判断类型使用 constructor 和 Object.prototype.toString 判断类型JavaScript 类型及其转换JavaScript 函数参数传递cannot read property of undefined 问题解决方案分析一道网红题目JavaScript 类型判断…...

ubuntu禁用/启用图形界面
当安装了带图形界的ubuntu的时候,如果觉得图形界面占资源,就需要将图形界面关闭,关闭的方法如下: 1、 打开 /etc/default/grub,修改或增加如下参数: GRUB_CMDLINE_LINUX_DEFAULT"text" GRUB_TE…...
——代码随想录算法训练营Day09)
【LeetCode】28. 找出字符串中第一个匹配项的下标(简单)——代码随想录算法训练营Day09
题目链接:28. 找出字符串中第一个匹配项的下标 题目描述 给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分ÿ…...

架设一台NFS服务器
1、开放/nfs/shared目录,供所有用户查询资料 2、开放/nfs/upload目录,为192.168.xxx.0/24网段主机可以上传目录, 并将所有用户及所属的组映射为nfs-upload,其UID和GID均为210 3、将/home/tom目录仅共享给192.168.xxx.xxx这台主机…...
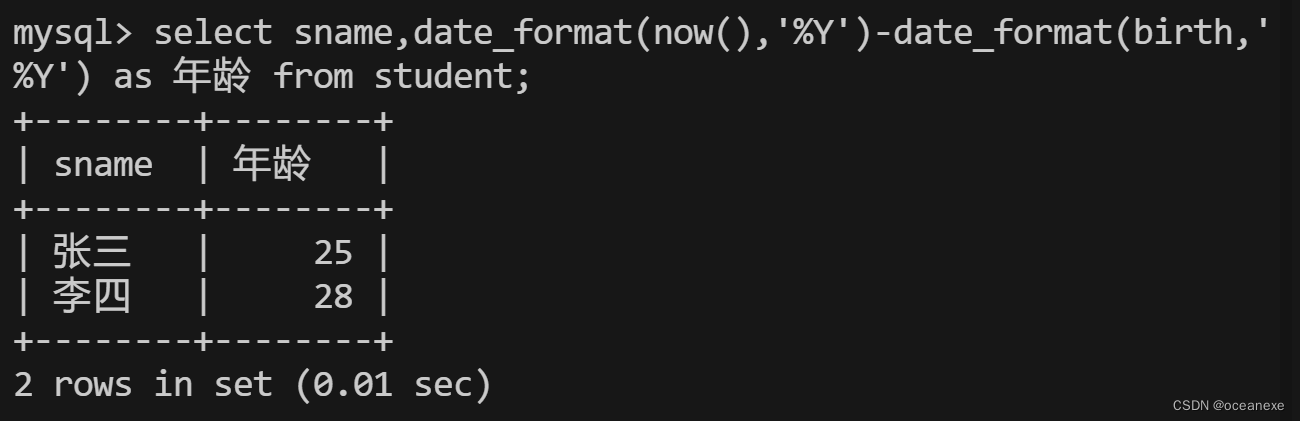
MySQL中根据出生日期计算年龄
创建student表 mysql> create table student( -> sid int primary key comment 学生号, -> sname varchar(20) comm…...
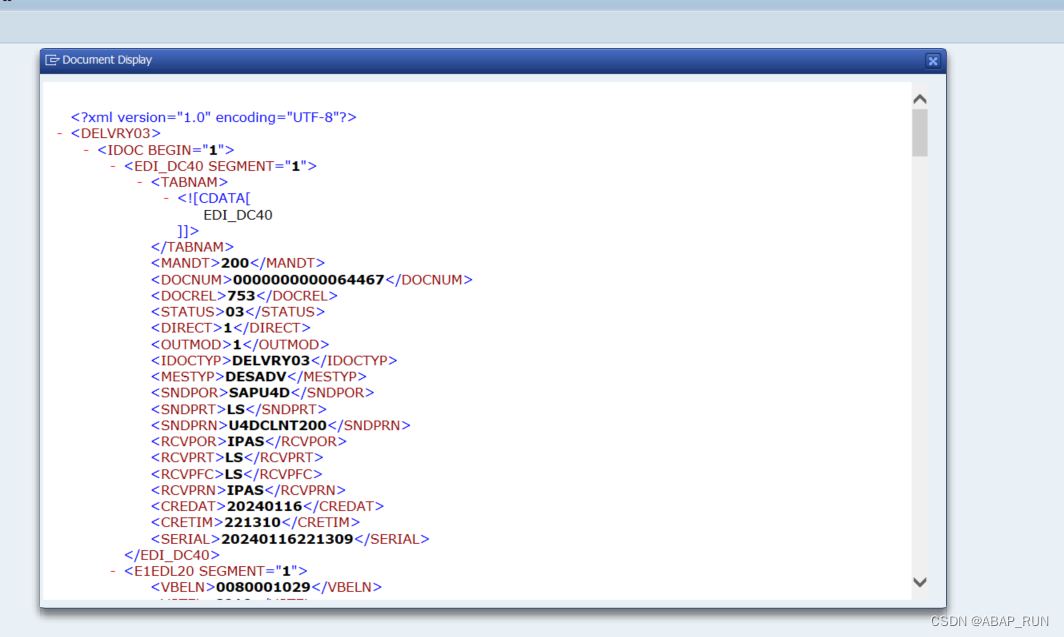
ABAP IDOC 2 XML
有个需求,外围系统希望我们给到一个IDOC 记录的样例,但是我们we02中并无法看到 就找了一个demo去直接展示IDOC内容 *&---------------------------------------------------------------------* *& Report Z_IDOC_TO_XML *&------------…...
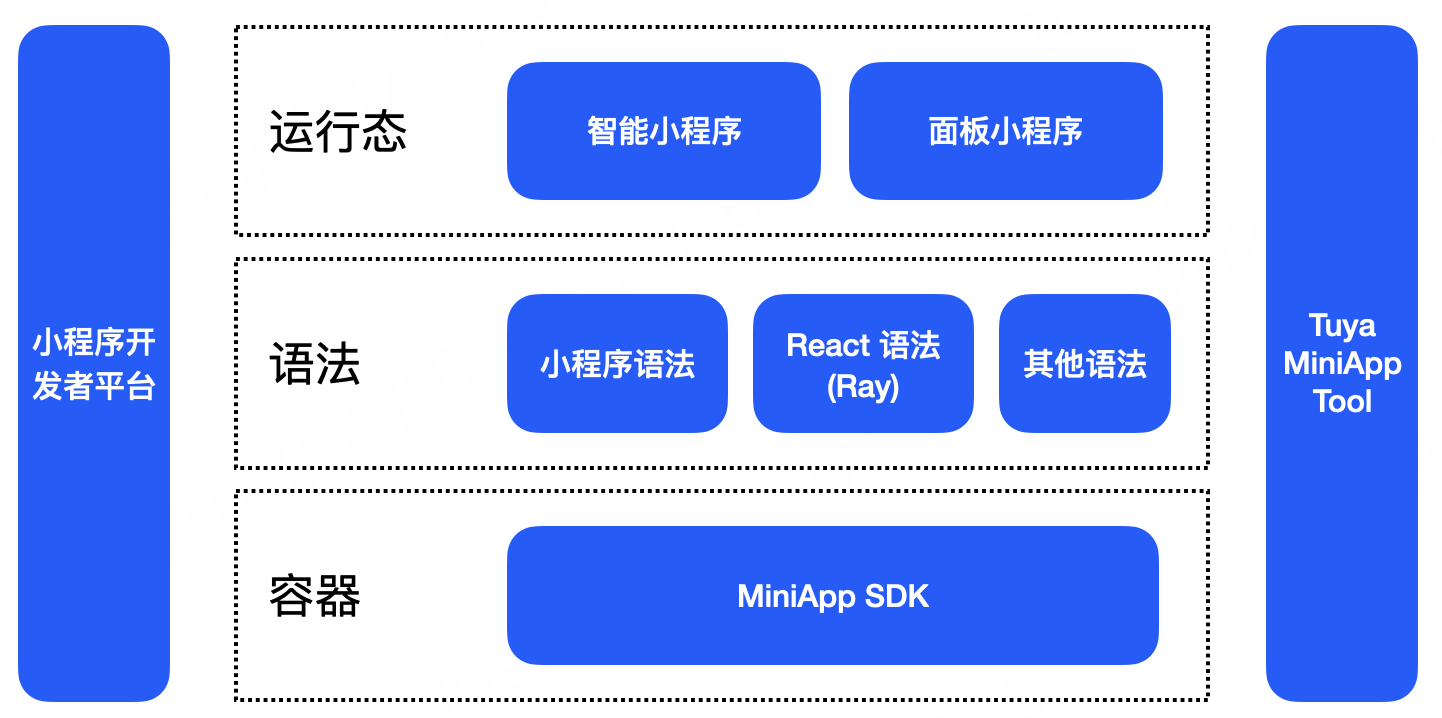
什么是小程序?特点和技术架构详解
小程序是一种新的移动应用程序格式,一种结合了 Web 技术以及客户端技术的混合解决方案。 传统的原生应用运行起来比较流畅,但是也有天然的基因缺陷: 不支持动态化,发布周期长需要开发Android和iOS两套代码,开发成本高…...

边缘计算的挑战和机遇——数据安全与隐私保护
边缘计算的挑战和机遇 边缘计算面临着数据安全与隐私保护、网络稳定性等挑战,但同时也带来了更强的实时性和本地处理能力,为企业降低了成本和压力,提高了数据处理效率。因此,边缘计算既带来了挑战也带来了机遇,需要我…...
)
linux-等保三级脚本(1)
该脚本主要是针对 CentOS Linux 7 合规基线加固的一些配置操作,包括创建用户、安全审计配置、入侵防范配置、访问控制配置、身份鉴别策略配置等。如果您需要在脚本中添加公司网址,您可以在适当的位置添加相应的内容。不过请注意,在实际生产环…...

K8s面试题——情景篇
文章目录 一、考虑一家拥有分布式系统的跨国公司,拥有大量数据中心,虚拟机和许多从事各种任务的员工。您认为这样公司如何以与 Kubernetes 一致的方式管理所有任务?二、考虑一种情况,即公司希望通过维持最低成本来提高其效率和技术运营速度。…...

.NET 8.0 发布到 IIS
如何在IIS(Internet信息服务)上发布ASP.NET Core 8? 在本文中,我假设您的 Windows Server IIS 上已经有一个应用程序池。 按照步骤了解在 IIS 环境下发布 ASP.NET Core 8 应用程序的技巧。 您需要设置代码以支持 IIS 并将项目配…...

当前vscode环境下 多进程多线程运行情况探究
我的代码 其中在“打开图片时”、“进入子进程之前”、“子进程join前”、“进入子进程区域后”,“子进程join后”、“进入子线程区域后”分别打印了进程线程的编号和数量。 # -*- coding: utf-8 -*-# Form implementation generated from reading ui file test2.…...

使用WAF防御网络上的隐蔽威胁之命令注入攻击
命令注入攻击是网络安全领域的一种严重威胁,它允许攻击者在易受攻击的应用程序上执行恶意命令。 这种攻击通常发生在应用程序将用户输入错误地处理为操作系统命令的情况下。 什么是命令注入攻击 定义:命令注入攻击发生在攻击者能够在易受攻击的应用程…...
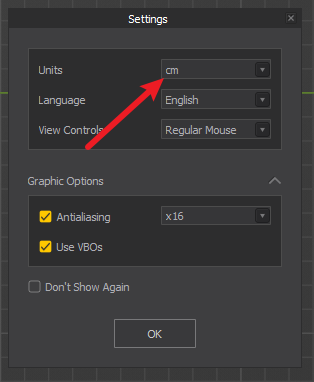
blender 导入到 Marvelous Designer
1) 将模型的所有部分合并为一个单独的mesh 2) 先调整计量单位: 3)等比缩放,身高调整到180cm左右 4)应用当前scale 首先,选中你要修改的物体,然后按下Ctrl-A键,打开应用…...
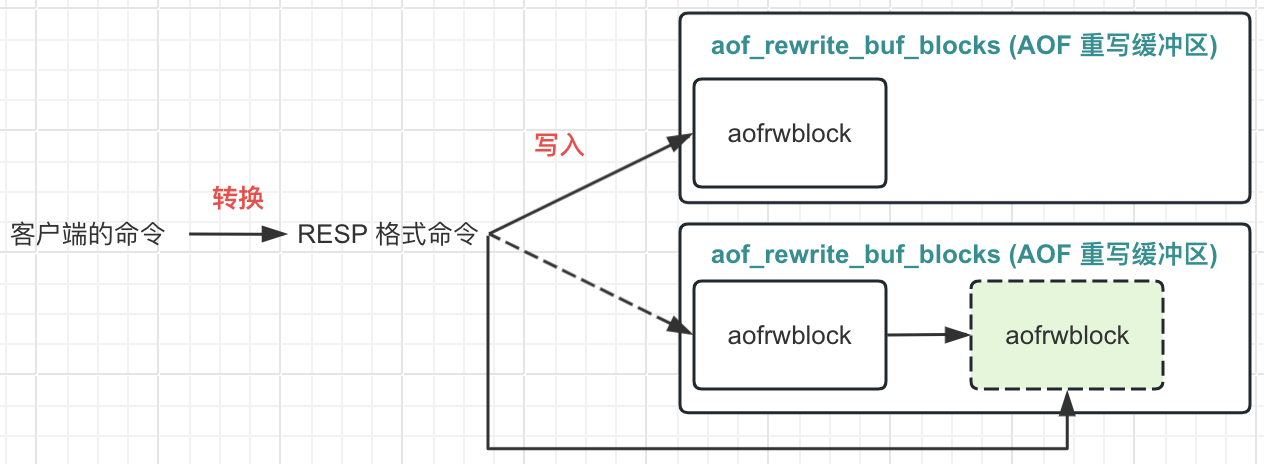
【Redis】AOF 源码
在上篇, 我们已经从使用 / 机制 / AOF 过程中涉及的辅助功能等方面简单了解了 Redis AOF。 这篇将从源码的形式, 进行深入的了解。 1 Redis 整个 AOF 主要功能 Redis 的 AOF 功能概括起来就 2 个功能 AOF 同步: 将客户端发送的变更命令, 保存到 AOF 文件中AOF 重写: 随着 Red…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
