AcGeMatrix2d::alignCoordSys一种实现方式
问题描述
此处为了简化问题,在2维空间中处理,按以下方式调用,AcGeMatrix2d::alignCoordSys是如何求出一个矩阵的呢,这里提供一个实现思路(但效率不保证好)
AcGeMatrix2d matTrans = AcGeMatrix2d::alignCoordSys(AcGePoint2d(150, 125),-AcGeVector2d::kYAxis,AcGeVector2d::kXAxis,AcGePoint2d(1000, 1000),AcGeVector2d::kXAxis,AcGeVector2d::kYAxis);
求解过程
AcGeMatrix2d::alignCoordSys函数的功能,即如何求出矩阵:
a11 a12 a13
a21 a22 a23
0 0 1
已知变量如下:
fromOriginX,fromOriginY =(150,125)
fromAxisXx, fromAxisXy = (0,-1)
fromAxisYx, fromAxisYy = (1,0)
toOriginX,toOriginY =(1000,1000)
toAxisXx, toAxisXy =(1,0)
toAxisYx, toAxisYy =(0,1)
根据对齐映射关系,得到如下等式
a11*fromOriginX + a12*fromOriginY + a13 = toOriginX
a21*fromOriginX + a22*fromOriginY + a23 = toOriginY
a11*fromAxisXx + a12*fromAxisXy + a13 = toAxisXx
a21*fromAxisXx + a22*fromAxisXy + a23 = toAxisXy
a11*fromAxisYx + a12*fromAxisYy + a13 = toAxisYx
a21*fromAxisYx + a22*fromAxisYy + a23 = toAxisYy
所以得到如下线性方程组
a11*150 + a12*125 + a13 = 1000
a21*150 + a22*125 + a23 = 1000
a11*0 + a12*-1 + a13 = 1
a21*0 + a22*-1 + a23 = 0
a11*1 + a12*0 + a13 = 0
a21*1 + a22*0 + a23 = 1
使用消元法求解即可(即用矩阵的初等变换将系数矩阵化为阶梯型矩阵)
相关文章:

AcGeMatrix2d::alignCoordSys一种实现方式
问题描述 此处为了简化问题,在2维空间中处理,按以下方式调用,AcGeMatrix2d::alignCoordSys是如何求出一个矩阵的呢,这里提供一个实现思路(但效率不保证好) AcGeMatrix2d matTrans AcGeMatrix2d::alignCo…...
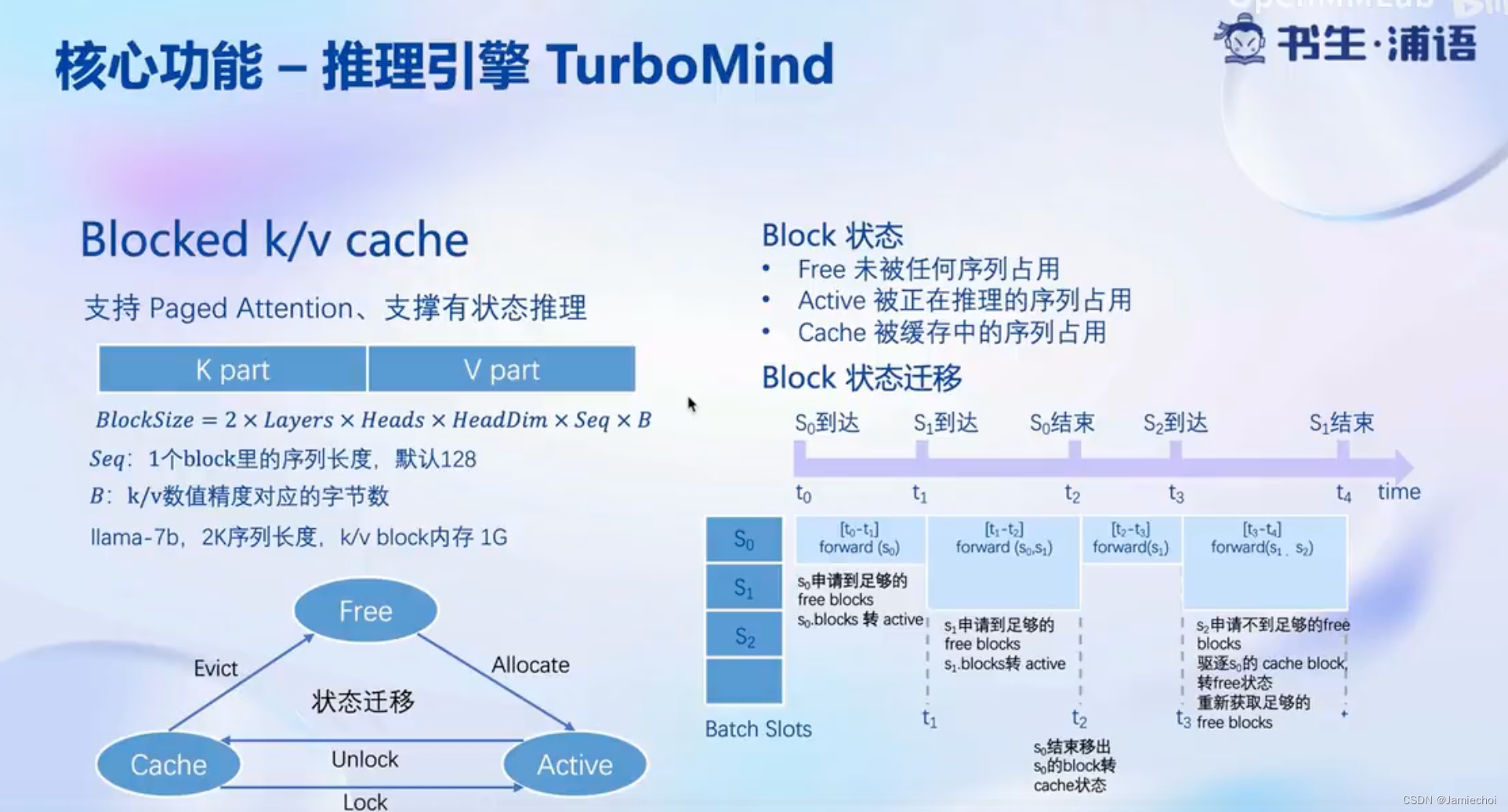
InternLM第5次课笔记
LMDeploy 大模型量化部署实践 1 大模型部署背景 2 LMDeploy简介 3 动手实践环节 https://github.com/InternLM/tutorial/blob/main/lmdeploy/lmdeploy.md 3...

2018年认证杯SPSSPRO杯数学建模D题(第一阶段)投篮的最佳出手点全过程文档及程序
2018年认证杯SPSSPRO杯数学建模 对于投篮最佳出手点的探究 D题 投篮的最佳出手点 原题再现: 影响投篮命中率的因素不仅仅有出手角度、球感、出手速度,还有出手点的选择。规范的投篮动作包含两膝微屈、重心落在两脚掌上、下肢蹬地发力、身体随之向前上…...
使用pdfbox 为 PDF 增加水印
使用pdfbox 为 PDF增加水印https://www.jylt.cc/#/detail?activityIndex2&idbd410851b0a72dad3105f9d50787f914 引入依赖 <dependency><groupId>org.apache.pdfbox</groupId><artifactId>pdfbox</artifactId><version>3.0.1</ve…...

6.【CPP】Date类的实现
Date.h #pragma once using namespace std; #include<iostream>class Date {friend ostream& operator<<(ostream& out, const Date& d);friend istream& operator>>(istream& in, Date& d); public://构造函数会被频繁调用,放在类…...
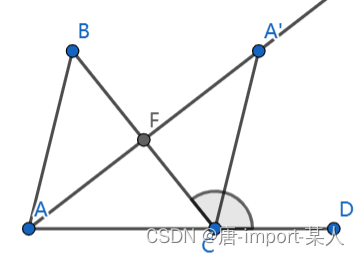
三角形任意一外角大于不相邻的任意一内角
一.代数证明 ∵ 对与△ A C B 中 ∠ c 外接三角形是 ∠ B C D ∵对与△ACB中∠c外接三角形是∠BCD ∵对与△ACB中∠c外接三角形是∠BCD ∴ ∠ B C D π − ∠ C ∴∠BCD\pi-∠C ∴∠BCDπ−∠C ∵ ∠ A ∠ B ∠ C π ∵∠A∠B∠C\pi ∵∠A∠B∠Cπ ∴ ∠ B C D ∠ A ∠…...

【Spring Boot 3】【Redis】集成Lettuce
【Spring Boot 3】【Redis】集成Lettuce 背景介绍开发环境开发步骤及源码工程目录结构总结背景 软件开发是一门实践性科学,对大多数人来说,学习一种新技术不是一开始就去深究其原理,而是先从做出一个可工作的DEMO入手。但在我个人学习和工作经历中,每次学习新技术总是要花…...
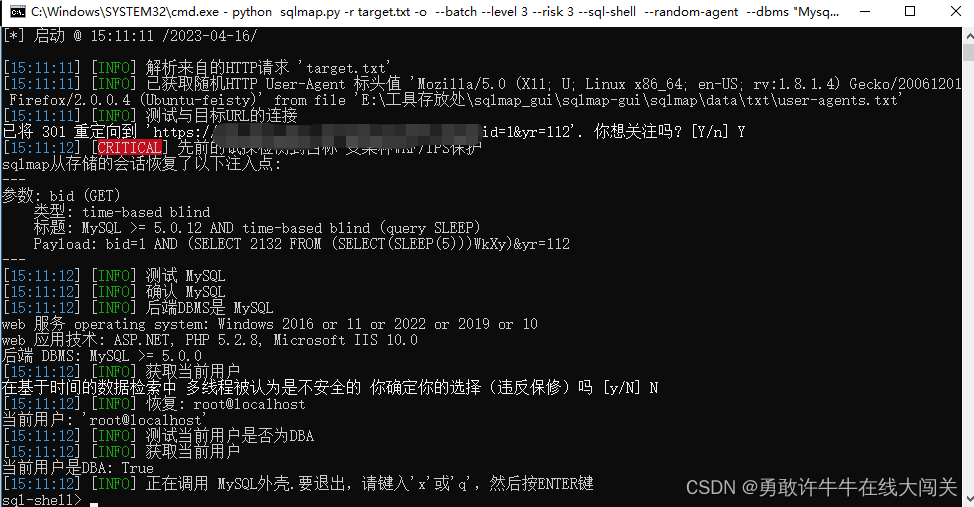
【SQL注入】SQLMAP v1.7.11.1 汉化版
下载链接 【SQL注入】SQLMAP v1.7.11.1 汉化版 简介 SQLMAP是一款开源的自动化SQL注入工具,用于扫描和利用Web应用程序中的SQL注入漏洞。它在安全测试领域被广泛应用,可用于检测和利用SQL注入漏洞,以验证应用程序的安全性。 SQL注入是一种…...
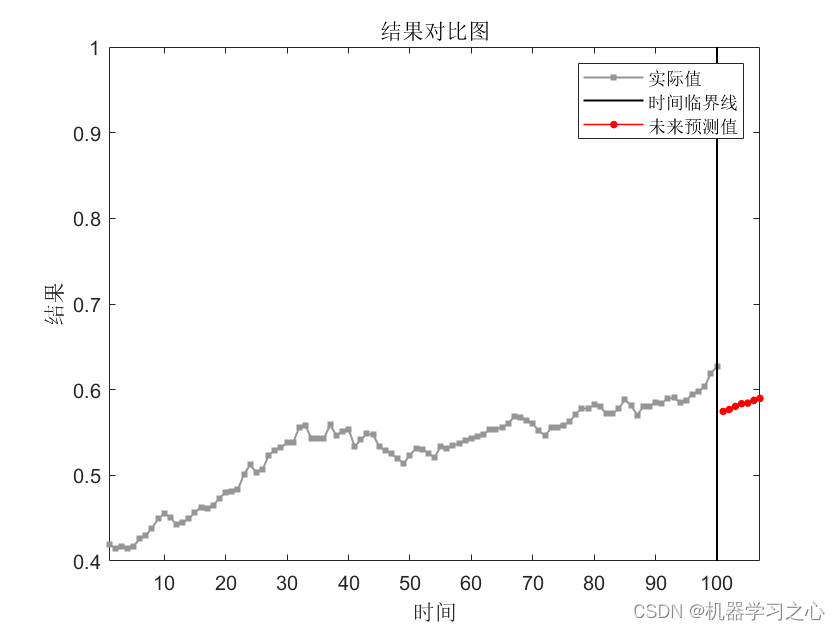
时序预测 | MATLAB实现GRNN广义回归神经网络时间序列未来多步预测(程序含详细预测步骤)
时序预测 | MATLAB实现GRNN广义回归神经网络时间序列未来多步预测(程序含详细预测步骤) 目录 时序预测 | MATLAB实现GRNN广义回归神经网络时间序列未来多步预测(程序含详细预测步骤)预测效果基本介绍程序设计参考资料预测效果 基本介绍 MATLAB实现GRNN广义回归神经网络时间序列…...

长期戴耳机的危害有哪些?戴哪种耳机不伤耳朵听力?
长期佩戴耳机可能会出现听力下降、耳道感染等危害。 听力下降:长时间戴耳机可能会导致耳道内的声音过大,容易对耳膜造成一定的刺激,容易出现听力下降的情况。 耳道感染:长时间戴耳机,耳道长期处于封闭潮湿的情况下&a…...

C++中的预处理
一.预定义符号 1.__FILE__进行编译的源文件 2.__LINE__文件当前的行号 3.__DATE__文件被编译的日期 4.__TIME文件被编译的时间 5.__STDC__如果编译器遵循ANSIC,其值为1,否则未定义 二.#define 基本语法:#define 名字 内容 eg.define M 1 经#define定义的常量时不经过…...
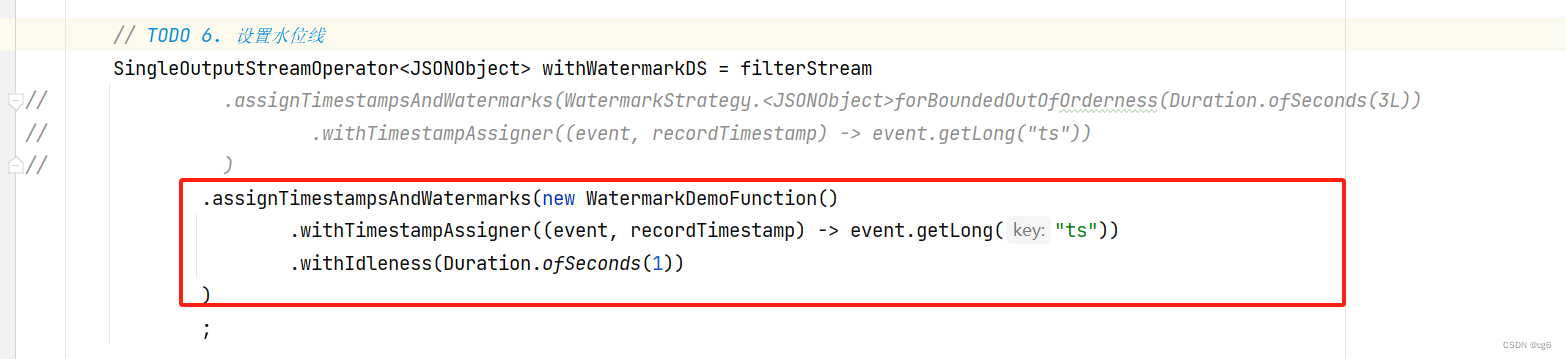
flink 最后一个窗口一直没有新数据,窗口不关闭问题
flink 最后一个窗口一直没有新数据,窗口不关闭问题 自定义实现 WatermarkStrategy接口 自定义实现 WatermarkStrategy接口 窗口类型:滚动窗口 代码: public static class WatermarkDemoFunction implements WatermarkStrategy<JSONObject…...

mybatis----小细节
1、起别名 在MyBatis中,<typeAliases>元素用于定义类型别名,它可以将Java类名映射为一个更简短的别名,这样在映射文件中可以直接使用别名而不需要完整的类名。 下面是一个示例: 在mybatis核心配置文件中配置typeAliases标…...

解密Oracle数据库引擎:揭开数据存储的神秘面纱
目录 1、介绍Oracle数据库引擎 1.1 什么是Oracle数据库引擎 1.2 Oracle数据库引擎的作用和功能 1.3 Oracle数据库引擎的历史和发展 2、Oracle数据库引擎的体系结构 2.1 Oracle数据库实例的组成部分 2.2 Oracle数据库引擎的层次结构 2.3 Oracle数据库引擎的关键组件 3、…...

「HDLBits题解」Karnaugh Map to Circuit
本专栏的目的是分享可以通过HDLBits仿真的Verilog代码 以提供参考 各位可同时参考我的代码和官方题解代码 或许会有所收益 相关资料:卡诺图化简法-CSDN博客 题目链接:Kmap1 - HDLBits module top_module(input a,input b,input c,output out );assig…...
由于找不到d3dcompiler_43.dll缺失,无法打开软件的解决方法分享
d3dcompiler43.dll是什么文件?为什么会出现丢失的情况?又该如何解决呢?本文将详细介绍d3dcompiler43.dll的作用和影响,并提供6个有效的解决方法。 一、d3dcompiler43.dll是什么文件? d3dcompiler43.dll是DirectX SDK…...
现阶段Python和Java哪个更吃香?
现阶段Python和Java哪个更吃香? 在开始前我有一些资料,是我根据网友给的问题精心整理了一份「Java的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!&…...

基于DNA的密码学和隐写术综述
摘要 本文全面调研了不同的脱氧核糖核酸(DNA)-基于密码学和隐写术技术。基于DNA的密码学是一个新兴领域,利用DNA分子的大规模并行性和巨大的存储容量来编码和解码信息。近年来,由于其相对传统密码学方法的潜在优势,如高存储容量、低错误率和对环境因素的抗性,该领域引起…...

【linux 多线程并发】多线程的控制,挂起线程暂停运行,直到唤醒线程,取消线程运行,可以设置合适的取消点属性避免不安全点被中止
线程运行控制 专栏内容: 参天引擎内核架构 本专栏一起来聊聊参天引擎内核架构,以及如何实现多机的数据库节点的多读多写,与传统主备,MPP的区别,技术难点的分析,数据元数据同步,多主节点的情况…...
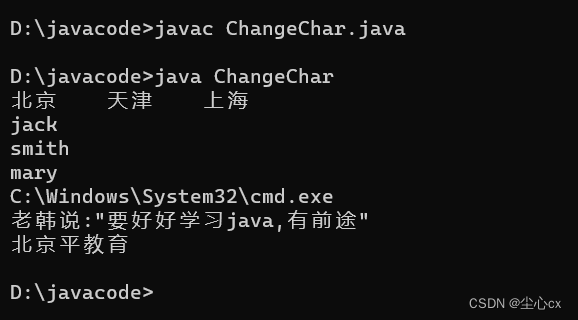
java转义字符
//转义字符的使用 public class ChangeChar{//编写一个main方法public static void main(String[] args){// \t :一个制表位,实现对齐的功能System.out.println("北京\t天津\t上海");// \n :换行符,实现换行System.out.println("jack\nsm…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...
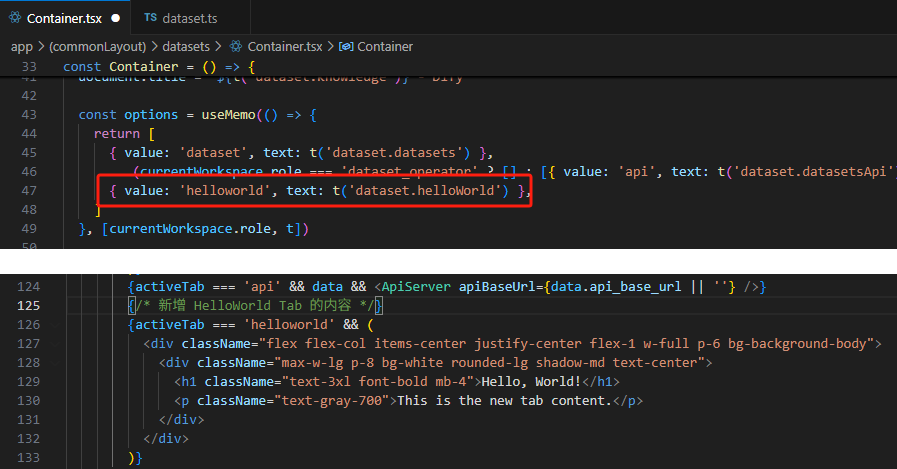
【技巧】dify前端源代码修改第一弹-增加tab页
回到目录 【技巧】dify前端源代码修改第一弹-增加tab页 尝试修改dify的前端源代码,在知识库增加一个tab页"HELLO WORLD",完成后的效果如下 [gif01] 1. 前端代码进入调试模式 参考 【部署】win10的wsl环境下启动dify的web前端服务 启动调试…...

第2篇:BLE 广播与扫描机制详解
本文是《BLE 协议从入门到专家》专栏第二篇,专注于解析 BLE 广播(Advertising)与扫描(Scanning)机制。我们将从协议层结构、广播包格式、设备发现流程、控制器行为、开发者 API、广播冲突与多设备调度等方面,全面拆解这一 BLE 最基础也是最关键的通信机制。 一、什么是 B…...

链结构与工作量证明7️⃣:用 Go 实现比特币的核心机制
链结构与工作量证明:用 Go 实现比特币的核心机制 如果你用 Go 写过区块、算过哈希,也大致理解了非对称加密、数据序列化这些“硬核知识”,那么恭喜你,现在我们终于可以把这些拼成一条完整的“区块链”。 不过别急,这一节我们重点搞懂两件事: 区块之间是怎么连接成“链”…...
