【数据结构】二叉树(遍历,递归)
🌈个人主页:秦jh__https://blog.csdn.net/qinjh_?spm=1010.2135.3001.5343
🔥 系列专栏:《数据结构》https://blog.csdn.net/qinjh_/category_12536791.html?spm=1001.2014.3001.5482

目录
二叉树遍历规则
前序遍历
中序遍历
后序遍历
递归结构遍历
前序
中序
求节点个数
求叶子节点个数
求树的高度
求第k层节点个数
前言
💬 hello! 各位铁子们大家好哇。
今日更新了树的遍历,递归的相关内容
🎉 欢迎大家关注🔍点赞👍收藏⭐️留言📝
二叉树遍历规则

前序遍历
注意:N代表空
分析:根据前序遍历的规则(根左右),先访问根1,然后左子树2,2的左子树3,3的左子树是N,右子树也是N,然后返回到2的右子树N,然后返回到1的右子树4,接着是4的左子树5,5的左右子树都是N,然后返回到4的右子树6,6的左右子树都是N。
中序遍历
分析:根据规则(左根右),1的左子树2,2的左子树3,3的左子树N,起始即为N,接着是根3,接着是3的右子树N,返回到根2,然后是2的右子树N,返回到根1,接着是1的右子树,以此类推。
后序遍历
分析:过程变为左右根,其实质与前面两种一样。
递归结构遍历

上图是要遍历的树的模型。
前序
假设树已构建好,下图是前序遍历的函数,执行后即可得到前序遍历的结果。

下图是递归的流程图:
分析:开始先打印根1,然后递归调用根2,以此类推到3的左子树N。此时左子树遍历完,返回到3的右子树,每次调用完就返回到上一层的函数中。
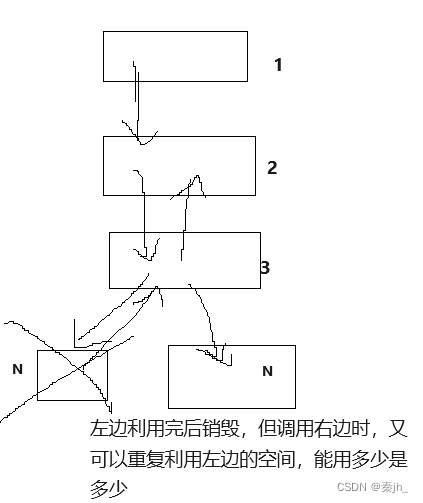
上图是递归调用占用的大致空间,每次调用完函数,返回到上一层,上一层接着调用,就会重复利用之前销毁的空间,如果空间不足,能用多少是多少。因此,递归的空间复杂度是看递归的深度。
中序

上图是中序遍历的函数,递归过程参考前序遍历过程。
后序遍历大致过程也同上,这里就不再写出。
求节点个数

递归过程图如下:

分析:如果根结点为空,则返回0。此递归过程会先找出左子树的节点个数,当遇到空节点时就返回0,然后加上根结点自身数量1,返回到上一层,以此类推。
求叶子节点个数
 参考前面的递归过程理解。
参考前面的递归过程理解。
求树的高度

求第k层节点个数
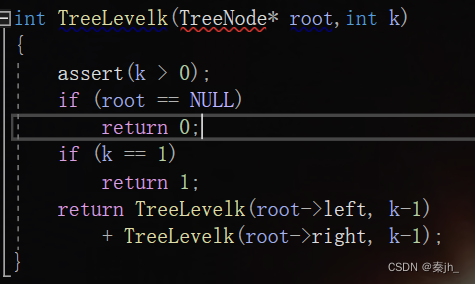
分析:k-1目的是当到达第k层后,直接返回1到上一层
我的博客即将同步至腾讯云开发者社区,邀请大家一同入驻:https://cloud.tencent.com/developer/support-plan?invite_code=3cd3jqfe6fwg0
相关文章:

【数据结构】二叉树(遍历,递归)
🌈个人主页:秦jh__https://blog.csdn.net/qinjh_?spm1010.2135.3001.5343🔥 系列专栏:《数据结构》https://blog.csdn.net/qinjh_/category_12536791.html?spm1001.2014.3001.5482 目录 二叉树遍历规则 前序遍历 …...

《微信小程序开发从入门到实战》学习八十五
6.15 设备API 6.15.2 添加联系人API 使用wx.addPhoneContact接口可以在用户的手机通讯录中添加联系人信息。用户可以选择“新增联系人”或“添加到已有联系人”。该接口接受Object参数,参支持属性如下所示: firstName:必填,名字…...

设计模式——命令模式
命令模式(Command Pattern)是一种行为型设计模式,它将一个请求封装为一个对象,使发出请求的对象和执行请求的对象解耦。这样可以方便地对请求排队、记录日志、撤销/重做操作以及支持可扩展性。 原理 命令接口(Comman…...

Modbus协议学习第三篇之协议通信规则
导语 本篇博客将深入介绍Modbus协议的一些内容,主要包括通讯方式和通讯模型的介绍 Modbus通讯方式 Modbus协议是单主机、多从机的通信协议,即同一时间,总线上只能有一个主设备,但可以有一个或者多个从设备(最多好像是2…...
git仓库使用说明
Git软件使用 1.先下载git相关软件 下载地址: Git - Downloading Package (git-scm.com) 下载其中一个安装 2.打开gitee网站,注册账号 3.打开个人中心,选择ssh公钥,查看如何生成公钥 4.生成公钥后,添加相应的公钥 …...

边缘计算和联邦学习的联系
1. 什么是边缘计算? 边缘计算(Edge Computing)是一种计算模型,其主要思想是将计算、存储和数据处理能力推送到离数据源近的边缘设备,而不是依赖于远程的云服务器。这样做的目的是减少数据传输延迟、提高响应速度&…...
机器学习算法理论:贝叶斯
贝叶斯定理对于机器学习来说是经典的概率模型之一,它基于先验信息和数据观测来得到目标变量的后验分布。具体来说,条件概率(也称为后验概率)描述的是事件A在另一个事件B已经发生的条件下的发生概率,公式表示为P(A|B)&a…...
】手机App防沉迷系统(模拟-JavaPythonC++JS实现))
229.【2023年华为OD机试真题(C卷)】手机App防沉迷系统(模拟-JavaPythonC++JS实现)
🚀点击这里可直接跳转到本专栏,可查阅顶置最新的华为OD机试宝典~ 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目-手机App防沉迷系统二.解题思路三.题解代码Pyth…...
关系运算符
Oracle从入门到总裁:https://blog.csdn.net/weixin_67859959/article/details/135209645 补充: 如果要想对所选择的数据行进行控制,那么可以利用 WHERE 子句完成,此时的 SQL 语法结构变为如下形式 先系统性介绍下: ● 关系运算: >、、&…...
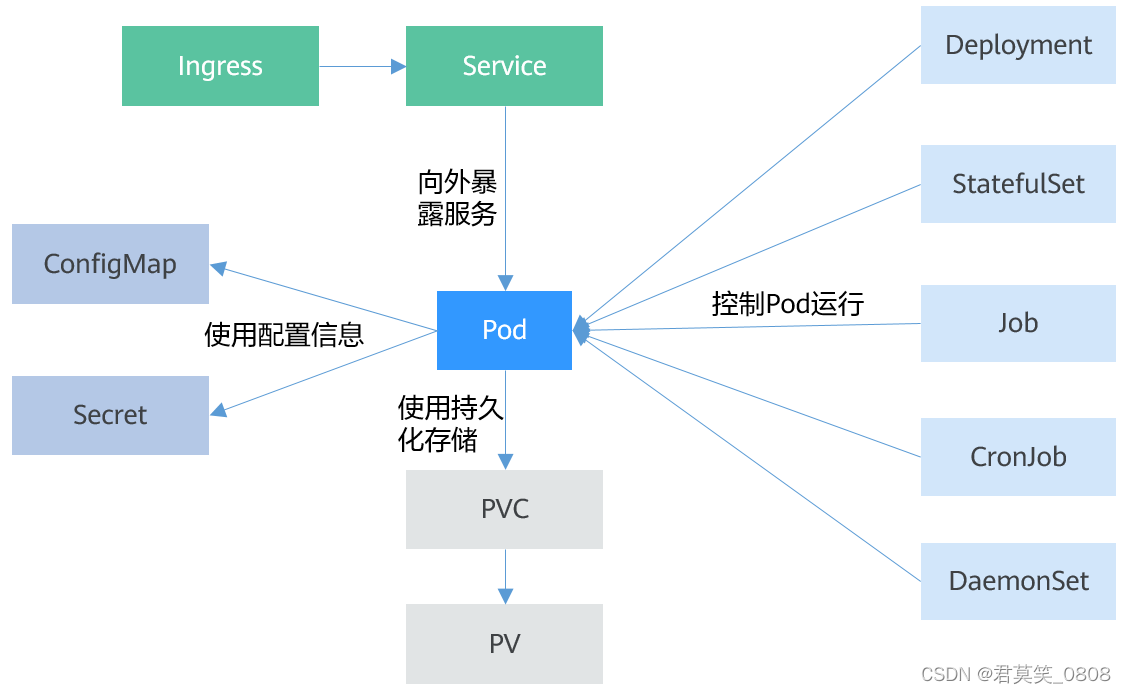
K8s-架构
一、K8s节点划分 K8s集群包含Master(控制节点)和Node(工作节点),应用部署在Node节点上。 集群架构图: 二、Master节点 Master节点分成四个组件:scheduler、ApiServer、Controller Manager、ETCD。类似三层结构,controller&#…...

C++ 并发编程 | 进程与线程
一、进程与线程 1、进程 1.1、定义 操作系统中最核心的概念就是进程,进程是对正在运行中的程序的一个抽象,是系统进行资源分配和调度的基本单位。进程是一种抽象的概念,一般由程序、数据集合和进程控制块三部分组成,如下&#x…...
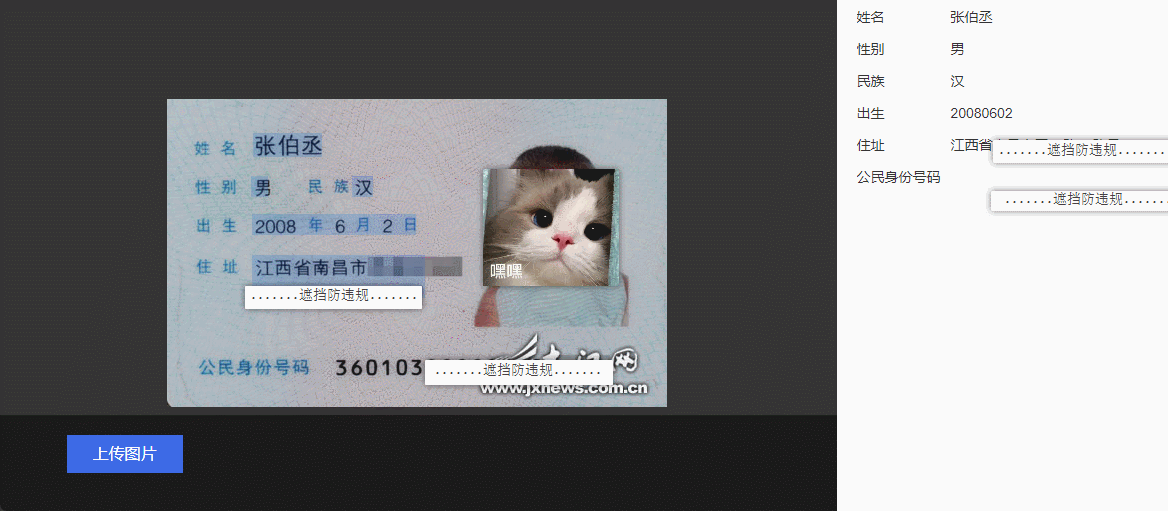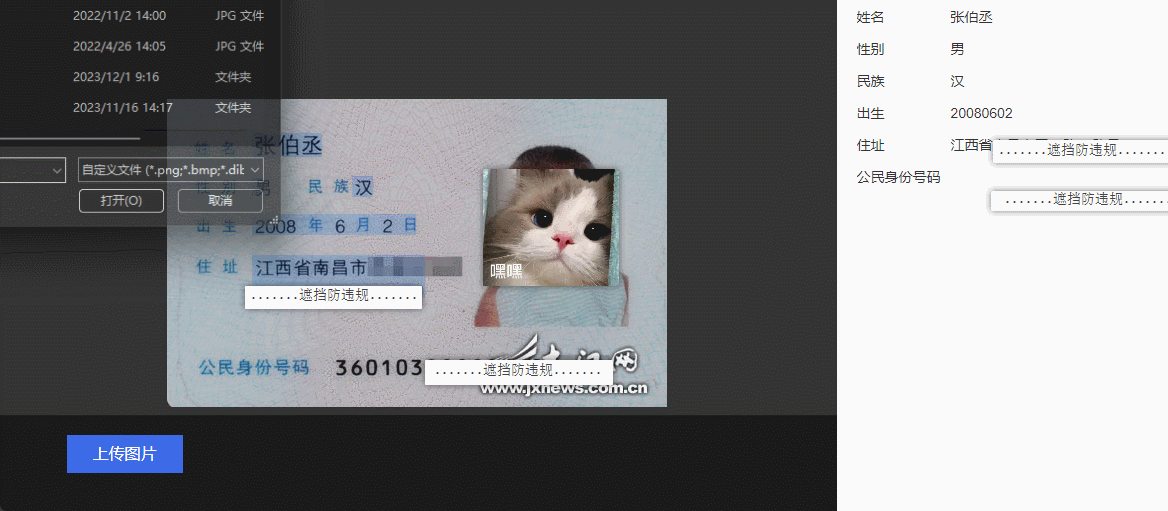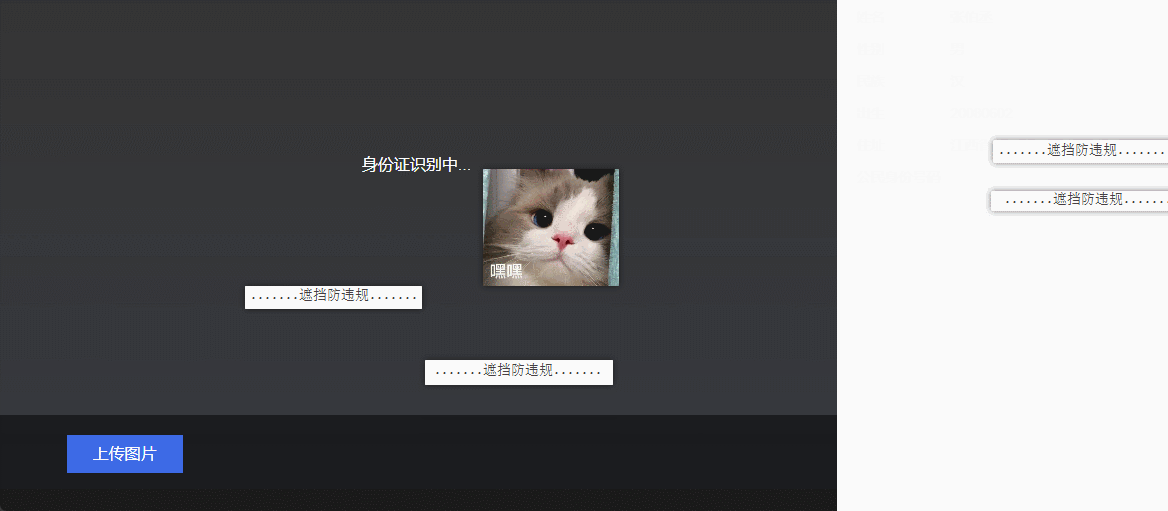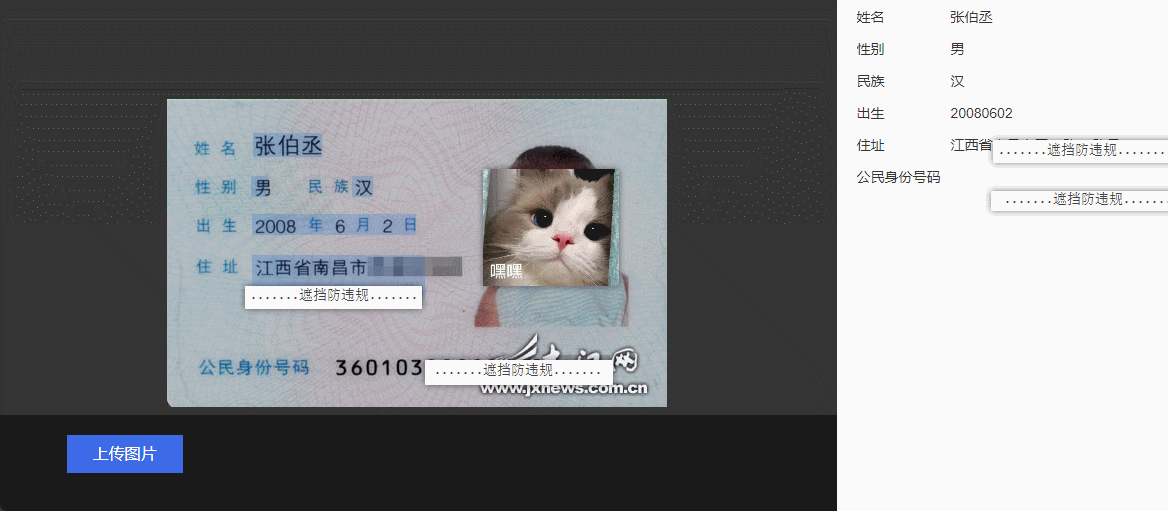
基于Python实现身份证信息识别
目录 前言身份证信息识别的背景与意义自动识别身份证的需求实现环境与工具准备Python编程语言OpenCV图像处理库Tesseract OCR引擎身份证信息识别算法原理图像预处理步骤(图像裁剪、灰度化 、二值化、去噪)信息提取与解析Python代码实现通过OCR提取身份证号码代码解析身份证信息…...
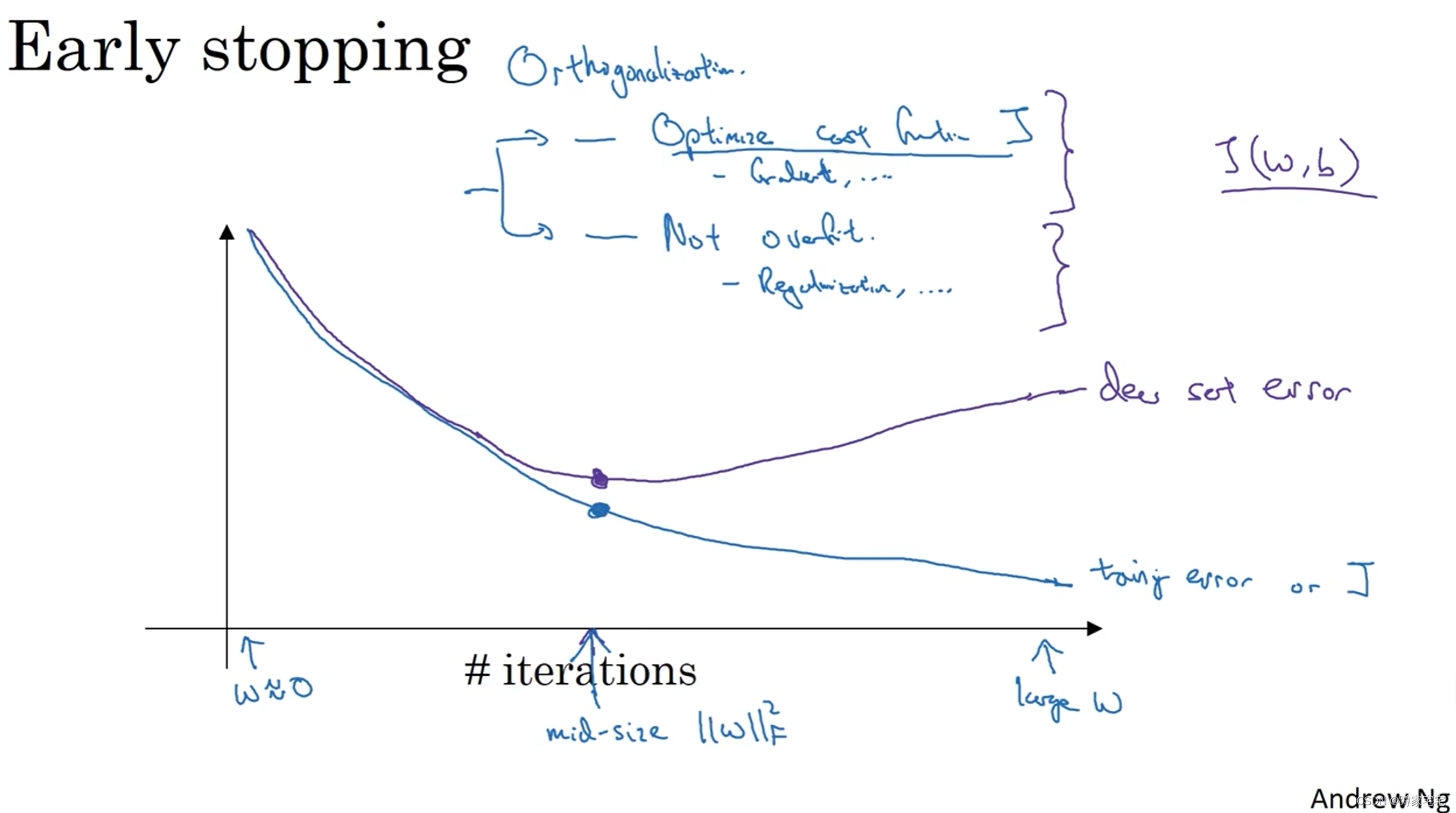
深度学习记录--正则化(regularization)
什么是正则化? 正则化(regularization)是一种实用的减少方差(variance)的方法,也即避免过度拟合 几种正则化的方法 L2正则化 又被称为权重衰减(weight dacay) 在成本函数中加上正则项: 其中 由于在w的更新过程中会递减,即权…...
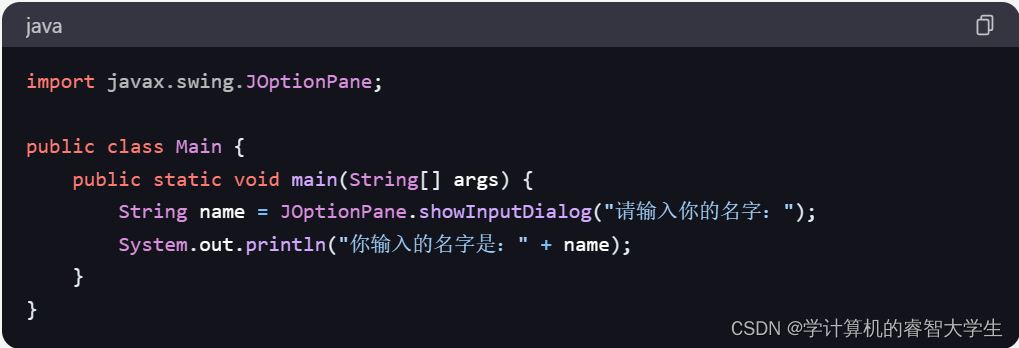
Java的便捷输入方法及解析
在 Java 中,有多种便捷的输入方法可以从用户那里获取输入。下面是一些常见的便捷输入方法及解析: 使用 Scanner 类:在上述示例中,首先导入了 java.util.Scanner 类,创建了一个 Scanner 对象,并使用 System…...
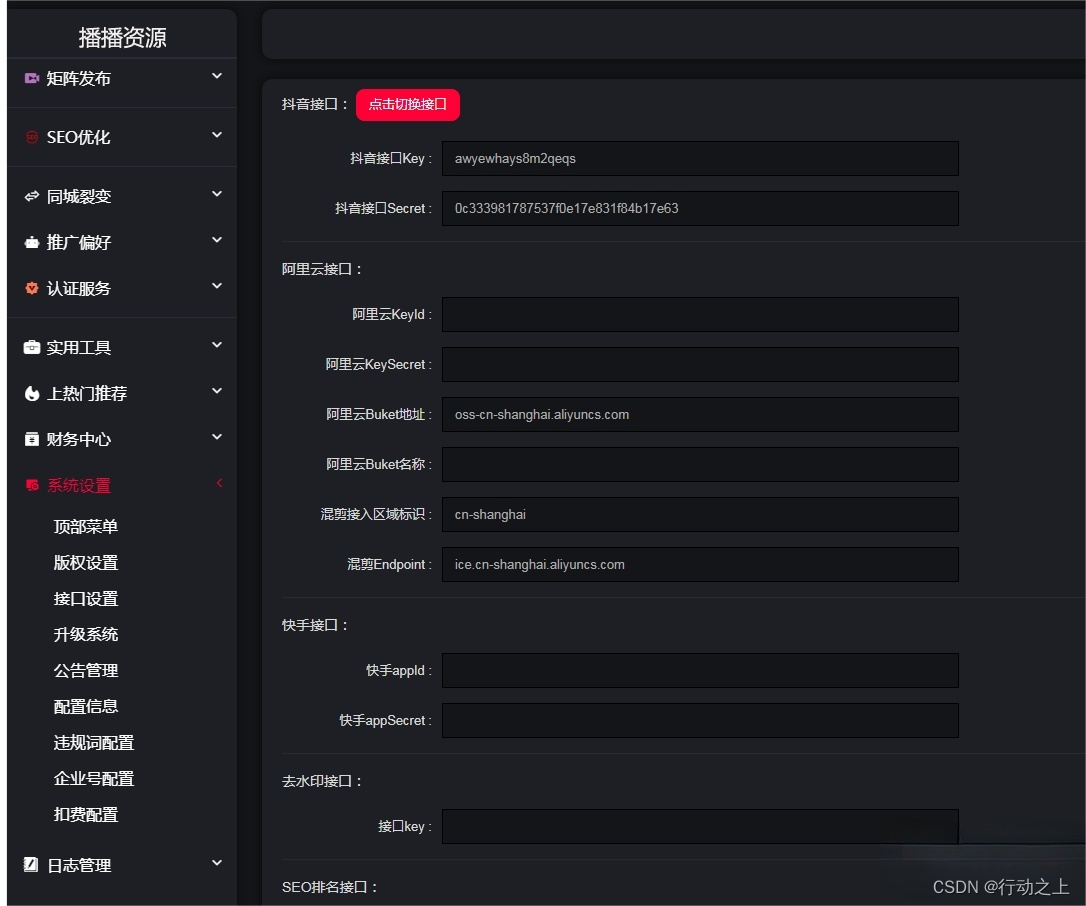
抖音矩阵云混剪系统源码(免授权版)多平台多账号一站式管理,附带系统搭建教程
搭建教程 MySQL 5.6 PHP 7.2 Apache 数据库名称 juzhen Nginx环境切换伪静态 1、解压安装包到项目根目录,找到application/database.php 更换自己的数据库密码 2、阿里云现有的配置不要动 其他按照文档进行添加 3、项目访问目录:public 4、域名…...
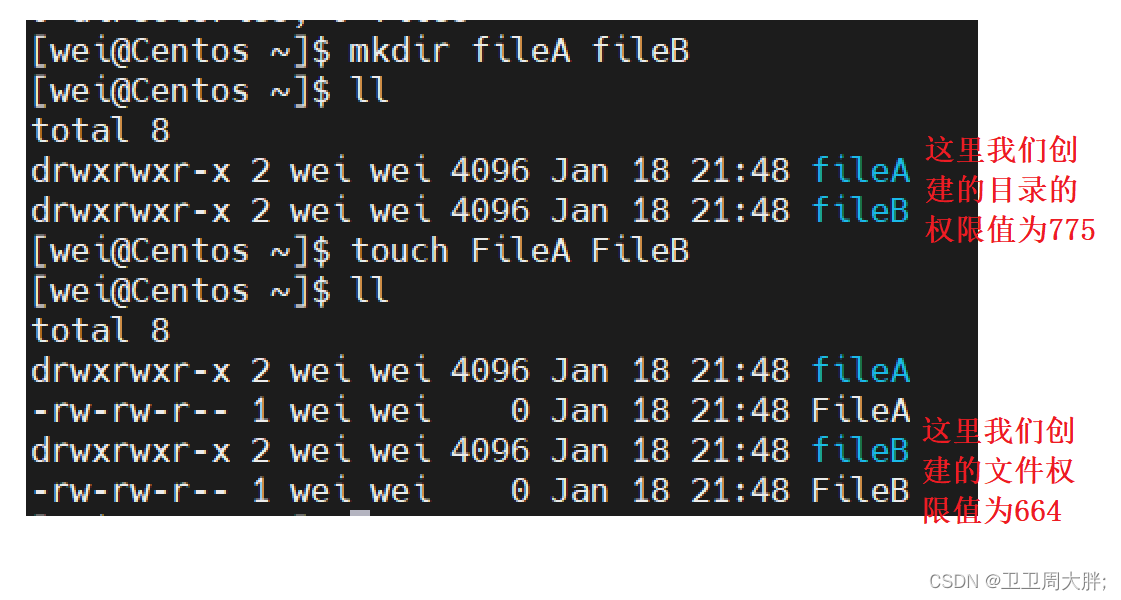
【Linux】权限的深度解析
前言:在此之前我们学习了一些常用的Linux指令,今天我们进一步学习Linux下权限的一些概念 💖 博主CSDN主页:卫卫卫的个人主页 💞 👉 专栏分类:Linux的学习 👈 💯代码仓库:卫卫周大胖的学习日记&a…...

c++函数怎么返回多个值
文章目录 使用结构体或类:定义一个结构体或类,其中包含了所有需要返回的值。然后在函数中返回这个结构体或类的实例。 struct Result {int value1;double value2;char value3; };Result myFunction() {Result r;r.value1 1;r.value2 2.0;r.value3 a;r…...
)
《剑指 Offer》专项突破版 - 面试题 15 : 字符串中的所有变位词(C++ 实现)
题目链接:LCR 015. 找到字符串中所有字母异位词 - 力扣(LeetCode) 题目: 输入字符串 s1 和 s2,如何找出字符串 s2 的所有变位词在字符串 s1 中的起始下标?假设两个字符串中只包含英文小写字母。例如&…...

03 SpringMVC响应数据之接收Cookie和请求头+原生API+共享域对象操作
下载postman,测试传json数据 1. 接收cookie 用CookieValue注解将cookie值绑定到控制器中的handler参数。 Controller类中的一个handler GetMapping("/CookieTest") public void handle(CookieValue("cookie的id(name)") String cookie) { //... }2. 接收…...

数据仓库(3)-模型建设
本文从以下9个内容,介绍数据参考模型建设相关内容。 1、OLTP VS OLAP OLTP:全称OnLine Transaction Processing,中文名联机事务处理系统,主要是执行基本日常的事务处理,比如数据库记录的增删查改,例如mysql、oracle…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...