【动态规划】24子数组系列_最长湍流子数组_C++
题目链接:最长湍流子数组
目录
题目解析:
算法原理
1.状态表示
2.状态转移方程
3.初始化
4.填表顺序
5.返回值
编写代码
题目解析:

题目让我们求返回 arr 的 最大湍流子数组的长度
由题可得:
如果比较符号在子数组中的每个相邻元素对之间翻转,则该子数组是 湍流子数组;
算法原理:
1.状态表示
先创建一个dp表
首先先思考dp表里面的值所表示的含义(是什么?)
这里我们需要两个dp表:
f[i]:以i位置为结尾,i位置为“上升”的最大湍流子数组的长度
g[i]:以i位置为结尾,i位置为“下降”的最大湍流子数组的长度
这种状态表示怎么来的?
1.经验+题目要求
用之前或者之后的状态,推导出dp[i][j]的值;
根据最近的最近的一步,来划分问题
经验:以i位置为结尾;
题目让我们返回 arr 的 最大湍流子数组的长度 ,
所以我们可以先设一个“dp表”表示以i位置为结尾,i位置最大湍流子数组的长度。
但是我们会发现:
只有一个dp表无法表示该位置的状态,状态分得还不够细(是>还是<)
所以这里我们尝试再加一个状态表示:
f[i]:以i位置为结尾,i位置为“上升”的最大湍流子数组的长度
g[i]:以i位置为结尾,i位置为“下降”的最大湍流子数组的长度
2.状态转移方程
dp[i]等于什么?
以i位置为结尾有三种情况:
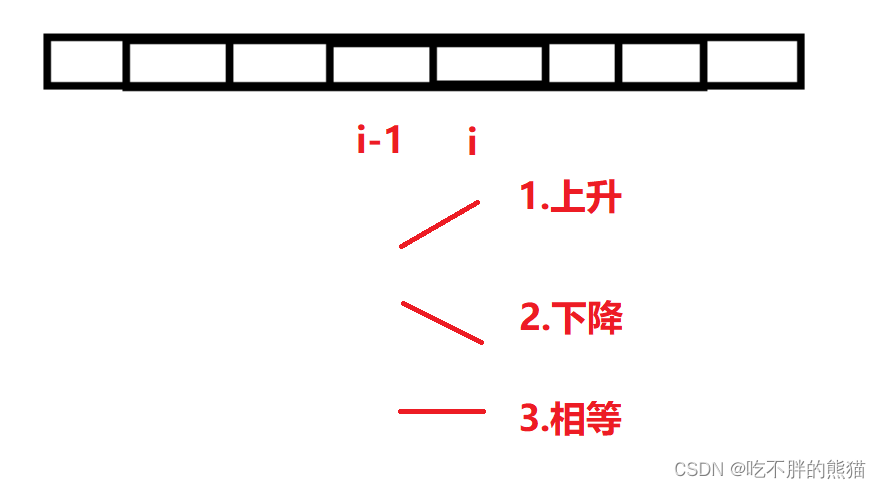
只有是情况1和2时才有可能时湍流子数组;
根据我们的状态表示:
情况一(i位置为“上升”):
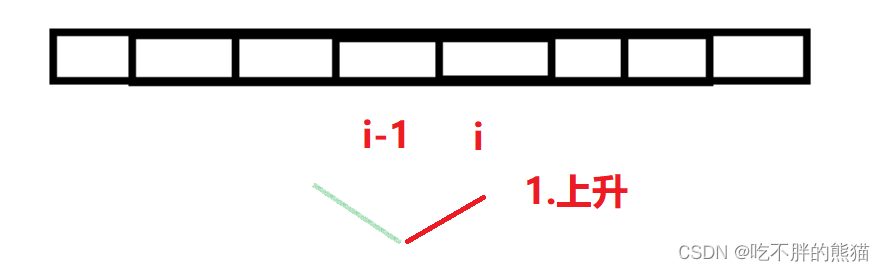
那么需要前面一个位置是“下降”的才满足湍流子数组;
所以此时i位置的最长湍流子数组应该是前面一个位置为“下降”的最长湍流子数组的长度+1;
而“前面一个位置为“下降”的最长湍流子数组的长度”就是我们的状态表示:g[i-1]
所以:f[i]=g[i-1]+1
情况二(i位置为“下降”):
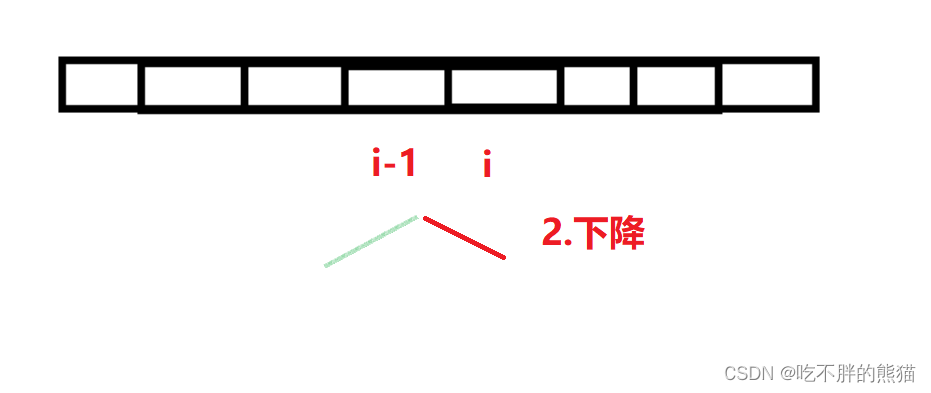
那么需要前面一个位置是“上升”的才满足湍流子数组;
所以此时i位置的最长湍流子数组应该是前面一个位置为“上升”的最长湍流子数组的长度+1;
而“前面一个位置为“上升”的最长湍流子数组的长度”就是我们的状态表示:g[i-1]
所以:g[i]=f[i-1]+1
3.初始化
(保证填表的时候不越界)
我们是从第二个元素比的,所以把要把前面的都初始化为1
4.填表顺序
(为了填写当前状态的时候,所需要的状态已经计算过了)
这里所需要的状态是:[i-1]
所以填表顺序从左往右
5.返回值
(根据题目要求和状态表示)
综上分析:
返回值为:两个表里的最大值
编写代码:

class Solution {
public:int maxTurbulenceSize(vector<int>& arr) {//1.创建dp表//2.初始化//3.填表//4.返回结果int n=arr.size();vector<int> f(n+1,1);auto g=f;int ret=1;for(int i=2;i<n+1;i++){if(arr[i-1]>arr[i-2]){f[i]=g[i-1]+1;}else if(arr[i-1]<arr[i-2]){g[i]=f[i-1]+1;}ret=max({(int)ret,g[i],f[i]});}return ret;}
};相关文章:

【动态规划】24子数组系列_最长湍流子数组_C++
题目链接:最长湍流子数组 目录 题目解析: 算法原理 1.状态表示 2.状态转移方程 3.初始化 4.填表顺序 5.返回值 编写代码 题目解析: 题目让我们求返回 arr 的 最大湍流子数组的长度 由题可得: 如果比较符号在子数组中的…...
fastJson和jackson的日期数据处理
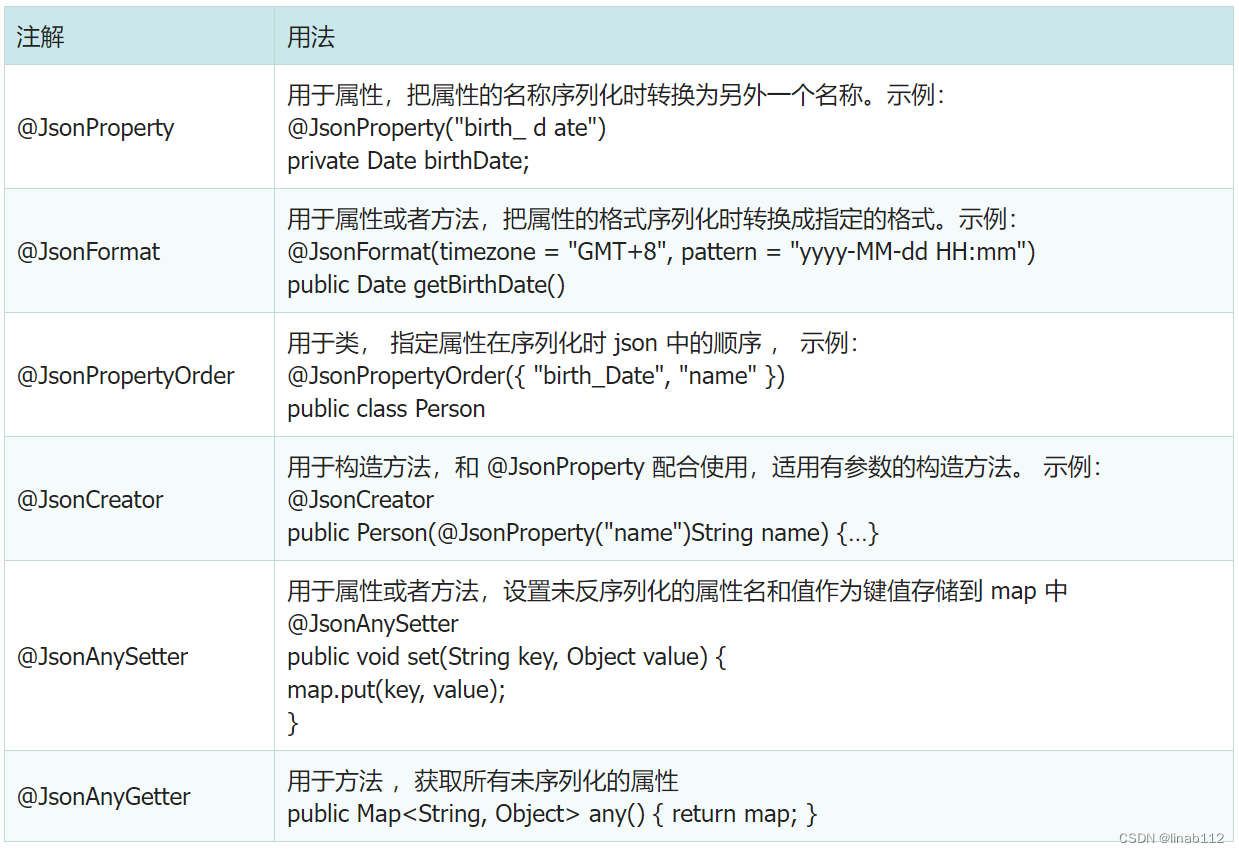
目录 1.jackson 2.fastjson 3.总结 1.jackson jackson是spring mvc默认的JSON解析方法,前端的数据序列化处理之后,后端经过反序列化处理可以直接使用实体对象进行接收。后端接口返回实体对象,经过序列化处理后前端可以接收并进行处理。 …...
书生·浦语大模型实战营第五节课笔记及作业
LMDeploy 大模型量化部署实践 1 大模型部署背景 1.1 模型部署及大模型特点 1.2 大模型部署挑战及方案 2 LMDeploy简介 2.1 核心功能-量化 2.2 核心功能-推理引擎TurboMind 2.1 核心功能-推理服务api server 3 动手实践及作业 按照文档LMDeploy 的量化和部署中的步骤在Intern…...

如何在CentOS 7 中基于OpenSSL 3.0 搭建Python 3.0 环境
1、OpenSSL 1.1 原因 [rootlocalhost ~]# openssl version OpenSSL 1.0.2k-fips 26 Jan 2017 [rootlocalhost ~]#通过执行openssl version可知Linux系统已经安装了OpenSSL,但该版本较低;Python 3 要求 OpenSSL版本不能低于1.1.1,否则安装P…...

爬虫接口获取外汇数据(汇率,外汇储备,贸易顺差,美国CPI,M2,国债利率)
akshare是一个很好用的财经数据api接口,完全免费!!和Tushare不一样。 除了我标题显示的数据外,他还提供各种股票数据,债券数据,外汇,期货,宏观经济,基金,银行…...

Spring Cloud和微服务架构的关系
大话Spring Cloud 在Java悠久的历史长河中(其实也就十来年),有一个框架自诞生之初就成了Java企业级开发领域的弄潮儿,它以开放的姿态不断引领着技术改革(我们管他叫Java领域的“改革开放”),它就是久经考验的企业级开发框架,改革…...

C++:通过ofstream写入二进制文件内容
C++:通过ifstream读取二进制文件内容_c++ ifstream 二进制读取-CSDN博客 介绍了读取二进制文件的方法。 本文介绍一下写入二进制数据到文件的方法: 1.通过write #include <fstream> #include <string> using namespace std; int main() {int data = 0x0102030…...

系统配置dns主从服务器
一、准备两台主机,区分主从 二、完全区域传送 1、主DNS服务器配置 #安装相关的包 [rootoula1 ~]# yum install bind -y#关闭防火墙 [rootoula1 ~]# systemctl stop firewalld [rootoula1 ~]# setenforce 0#修改配置主文件 [rootoula1 ~]# vim /etc/named.conf opt…...

【git】解决网络连接问题
ssh: connect to host github.com port 22: Connection timed out $ ssh: connect to host github.com port 22: Connection timed out fatal: Could not read from remote repository. bash: ssh:: command not found bash: fatal:: command not found无效 检查网络…...

限制API接口访问速率
文章目录 依赖注解aophelperTest 免责声明:本人无意侵权,奈何找不到原文作者,也找不到网址,于是自己记录一下,如果有侵权之嫌,请联系我删除文章 依赖 <!-- https://mvnrepository.com/artifact/com.goo…...

广东省第三届职业技能大赛“网络安全项目”B模块--数字取证解析
广东省第三届职业技能大赛“网络安全项目”B模块任务书 PS: 关注鱼影安全第一部分 网络安全事件响应第二部分 数字取证调查任务 3: 网络数据包分析取证解析:第三部分 应用程序安全:需要环境可以私信博主~PS: 关注鱼影安全 模块 B 竞赛项目试题 本文件为:广东省第三届职业技…...

全链路压力测试:现代软件工程中的重要性
全链路压力测试不仅可以确保系统在高负载下的性能和稳定性,还能帮助企业进行有效的风险管理和性能优化。在快速发展的互联网时代,全链路压力测试已成为确保软件产品质量的关键步骤。 1、测试环境搭建 测试应在与生产环境尽可能相似的环境中进行ÿ…...

【计算机网络】难点、易遗忘点总结
文章目录 1. 单工通信、半双工通信和全双工通信2. TCP的三次握手和四次挥手 1. 单工通信、半双工通信和全双工通信 主要区别在于信息传输的方向和时间安排。单工通信是指信息只能在一个方向上传输的通信方式。半双工通信允许信息在两个方向上传输,但在任何给定的时…...

谷达冠楠科技:抖音开网店新手小白可以卖的产品
随着互联网的发展,越来越多的人选择在网上开设自己的店铺。而抖音作为目前最火的短视频平台,也提供了开店的功能。那么,对于新手小白来说,抖音开网店可以卖哪些产品呢? 我们可以考虑的是服装类商品。抖音上有很多时尚博主&#x…...
爬虫案例—根据四大名著书名抓取并存储为文本文件
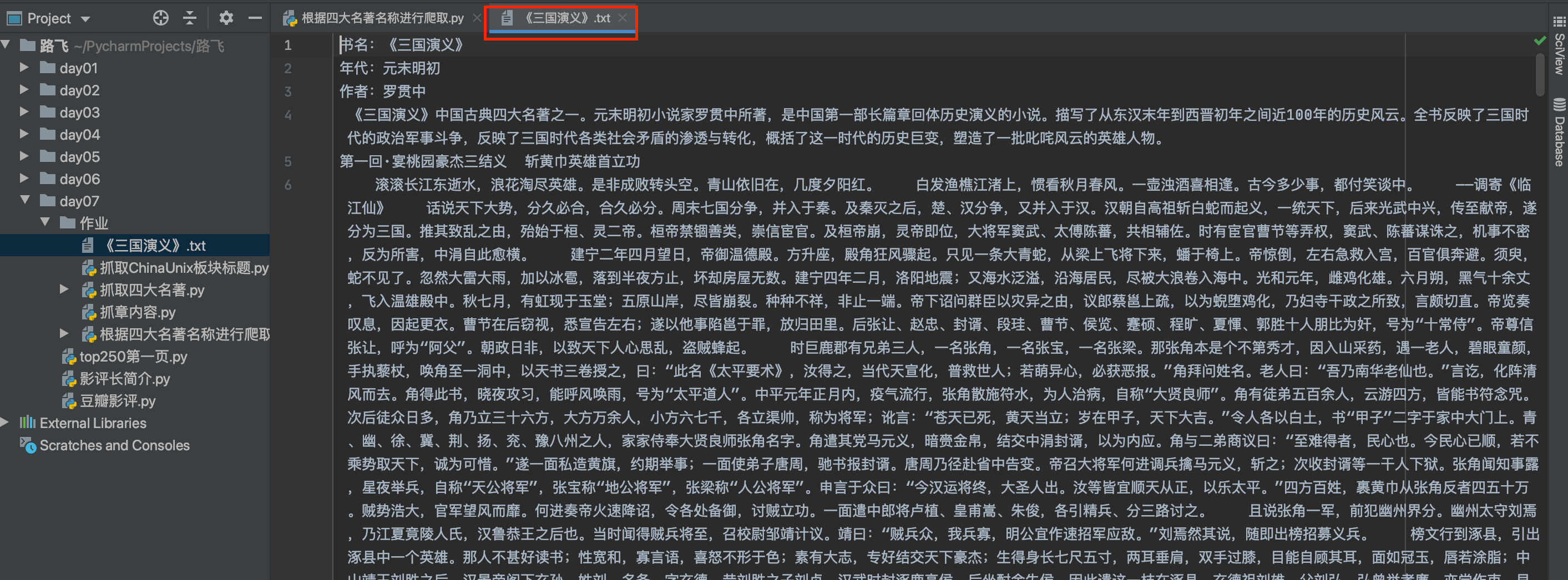
爬虫案例—根据四大名著书名抓取并存储为文本文件 诗词名句网:https://www.shicimingju.com 目标:输入四大名著的书名,抓取名著的全部内容,包括书名,作者,年代及各章节内容 诗词名句网主页如下图&#x…...
阿里云容器服务助力万兴科技 AIGC 应用加速
作者:子白(顾静) 2023 年堪称是 AIGC 元年,文生图领域诞生了 Stable Diffusion 项目,文生文领域诞生了 GPT 家族。一时间风起云涌,国内外许多企业投身 AIGC 创新浪潮,各大云厂商紧随其后纷纷推…...

STM32F103标准外设库——认识STM32(一)
个人名片: 🦁作者简介:一名喜欢分享和记录学习的在校大学生 🐯个人主页:妄北y 🐧个人QQ:2061314755 🐻个人邮箱:2061314755qq.com 🦉个人WeChat:V…...
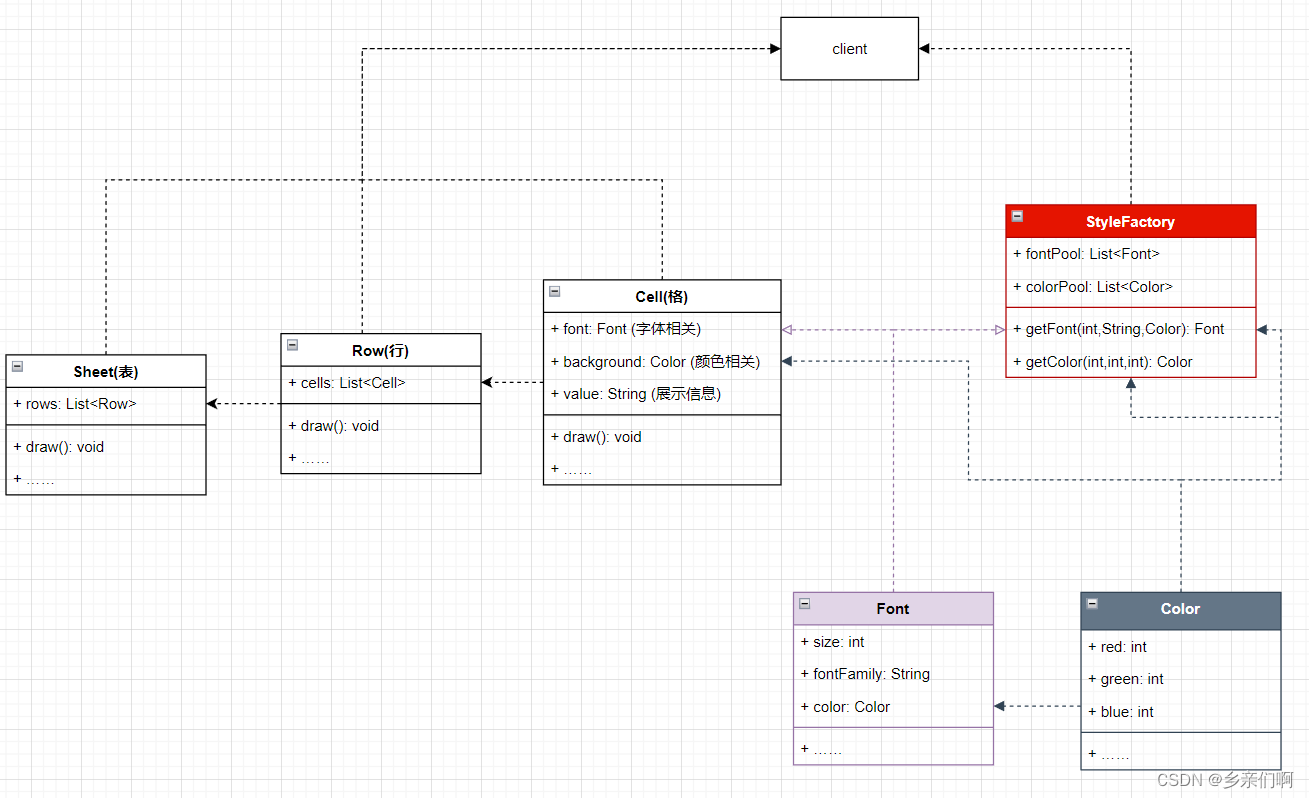
设计模式——1_5 享元(Flyweight)
今人不见古时月,今月曾经照古人 ——李白 文章目录 定义图纸一个例子:可以复用的样式表绘制表格降本增效?第一步,先分析 变化和不变的地方第二步,把变化和不变的地方拆开来第三步:有没有办法共享这些内容完…...
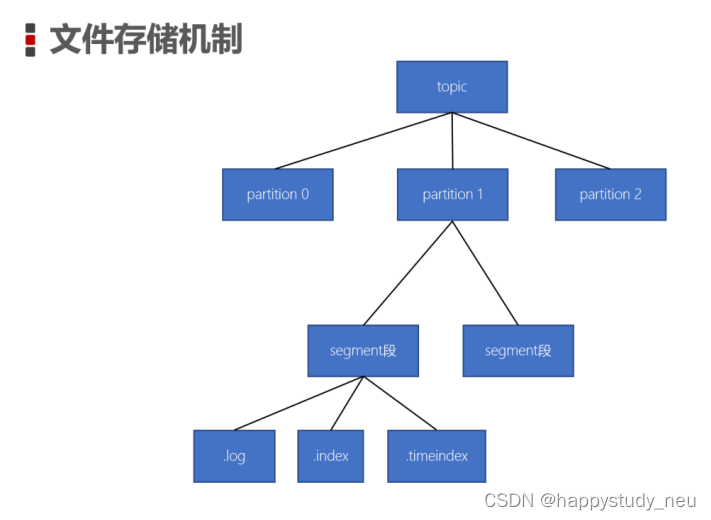
kafka系列(二)
本章承接kafka一内容,文章在本人博客主页都有,可以自行点击浏览。 幂等性 请求执行多次,但执行的结果是一致的。 如果,某个系统是不具备幂等性的,如果用户重复提交了某个表格,就可能会造成不良影响。例如…...
Ubuntu20.04安装配置OpenCV-Python库并首次执行读图
一、选择三方提供的预编译包安装: 可以从官网下载 OpenCV 的安装包,编译后使用;也可以直接使用第三方提供的预编译包 安装。显然后者不需要执行编译步骤,更便捷。选择由 PyPI 提供的 OpenCV 安装包,可以在 https://py…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...
