最优解-最长公共子序列
问题描述
最长公共子序列(Longest Common Subsequence,LCS)即求两个序列最长的公共子序列(可以不连续)。比如3 2 1 4 5和1 2 3 4 5两个序列,最长公共子序列为2 4 5 长度为3。解决这个问题必然要使用动态规划。既然要用到动态规划,就要知道状态转移方程。我们令L[i][j] 表示序列 A 和序列 B 的最长公共子序列的长度,则状态转移方程如下:
若a[i]=b[j], 则 L[i][j]=L[i-1][j-1] +1
若a[i]!=b[j], 则 L[i][j]=max (L[i][j-1],L[i-1][j])
即:相同的取左上加1,不同取上和左中的最大值
package com.algorithm;
/*** long common Subseq*/
public class LCS {public static void main(String[] args) {char[] seq1 = new char[]{'a','b','d','c','b','a','b'};char[] seq2 = new char[]{'b','d','c','b','a','b','b'};int[][] dp = new int[seq1.length + 1][seq2.length + 1];//存储两个序列当前i和j的公共序列长度,多存储一位是空字符,默认都市0//初始化for (int i = 0; i < seq1.length + 1; i++) {dp[i][0] = 0;}for (int j = 0; j < seq2.length + 1; j++) {dp[0][j] = 0;}//计算dp,相同的取左上加1,不同取上和左中的最大值for(int i = 1; i < seq1.length; i++) {for(int j = 1; j<seq2.length; j++) {if(seq1[i] == seq2[j]) {dp[i][j] = dp[i-1][j-1]+1; //左上加1} else {dp[i][j] = Math.max(dp[i][j-1],dp[i-1][j]); //上和左中的最大值}}}//获取最长公共子序列长度,也就是dp中最大的那个值int max = 0;for(int i = 1; i < dp.length; i++) {for (int j = 1; j < dp.length; j++) {max = Math.max(max, dp[i][j]);}}System.out.println("long common seq size:"+max);}
}
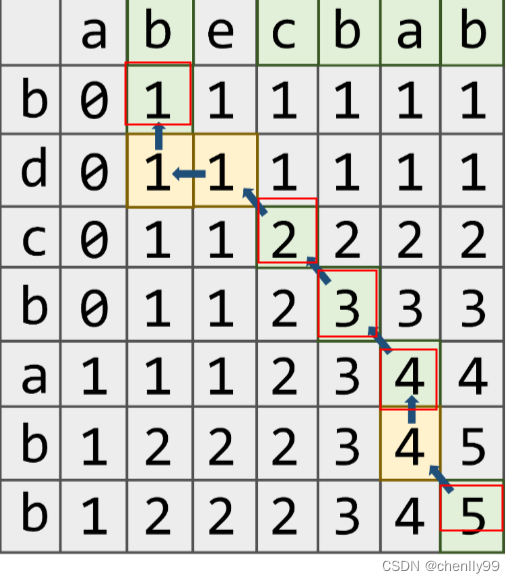
从右下角开始,如果有dp[i][j]==dp[i-1][j-1]+1则往左上走一格。得到整个子序列的求解过程。b,c,b,a,b
相关文章:

最优解-最长公共子序列
问题描述 最长公共子序列(Longest Common Subsequence,LCS)即求两个序列最长的公共子序列(可以不连续)。比如3 2 1 4 5和1 2 3 4 5两个序列,最长公共子序列为2 4 5 长度为3。解决这个问题必然要使用动态规划。既然要用到动态规划,就要知道状…...
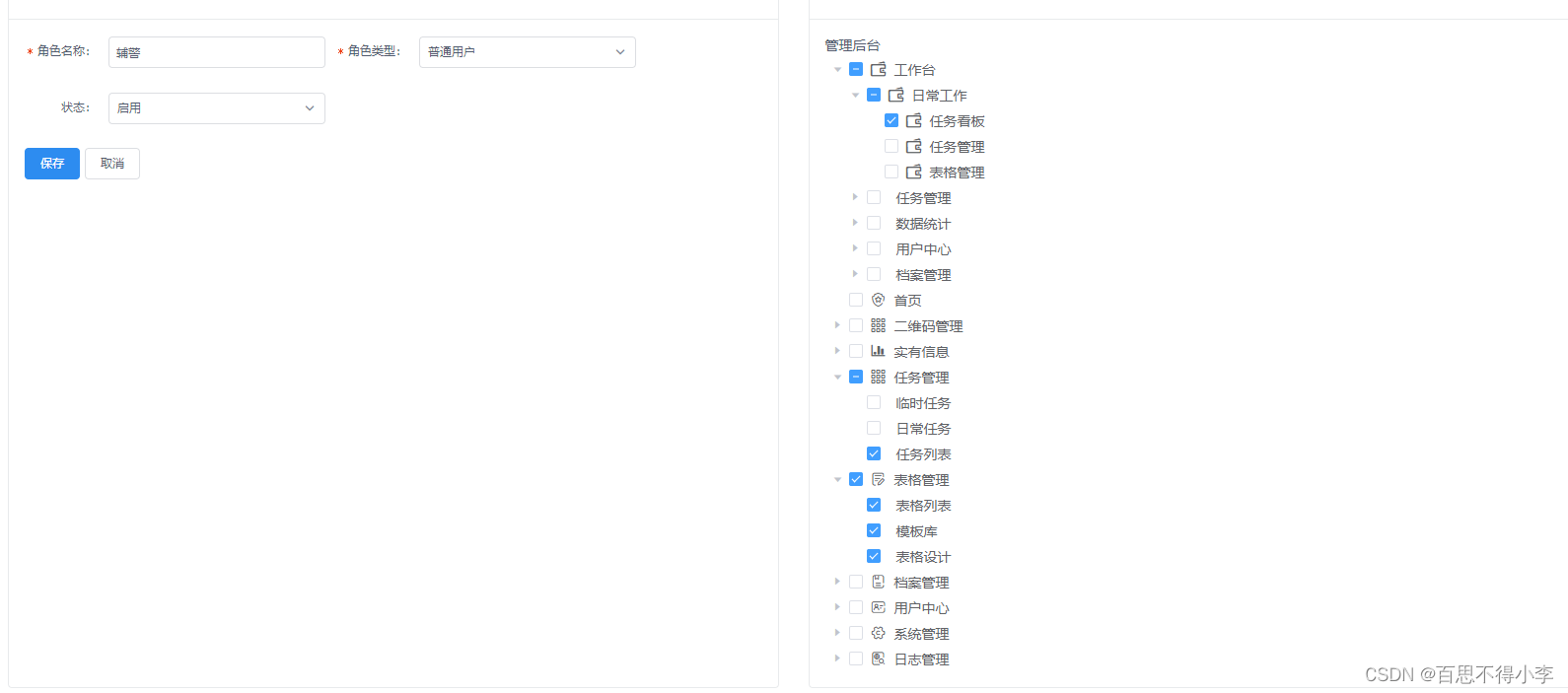
el-tree获取当前选中节点及其所有父节点的id(包含半选中父节点的id)
如下图,我们现在全勾中的有表格管理及其下的子级,而半勾中的有工作台和任务管理及其子级 现在点击保存按钮后,需要将勾中的节点id及该节点对应的父节点,祖先节点的id(包含半选中父节点的id)也都一并传给后端,那这个例子里就应该共传入9个id,我们可以直接将getCheckedK…...

新上线一个IT公司微信小程序
项目介绍 项目背景: 一家IT公司,业务包含以下六大块: 1、IT设备回收 2、IT设备租赁 3、IT设备销售 4、IT设备维修 5、IT外包 6、IT软件开发 通过小程序,提供在线下单,在线制单,在线销售,业务介绍,推广,会员 项目目的: 业务介绍: 包含企业业务介绍 客户需…...

MCAL配置-PWM(EB23.0)
PWM配置项的介绍 一、General 1、PwmDeInitApi 从代码中添加/删除Pwm_17_GtmCcu6_Delnit() API。 TRUE:Pwm_17_GtmCcu6_Delnit() API可供用户使用。 FALSE:Pwm_17_GtmCcu6_Delnit() API对用户不可用。 注意:默认情况下禁用Pwm_17_GtmCcu6_Delnit() …...
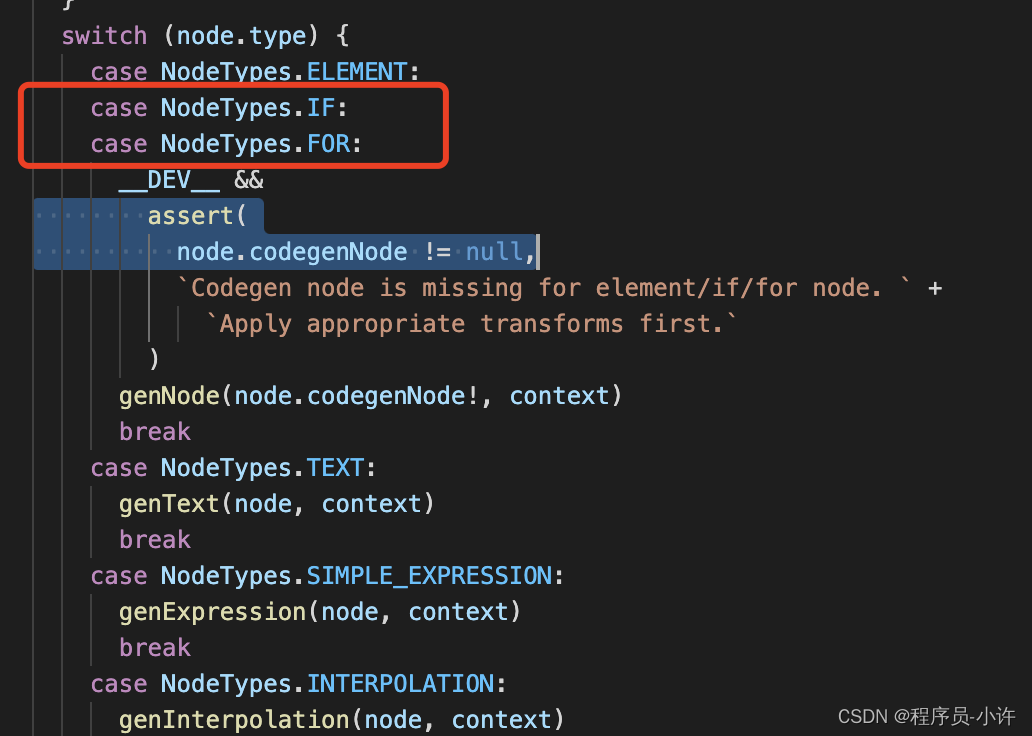
v-if和v-for哪个优先级更高?
v-if和v-for哪个优先级更高? 结论: vue2输出的渲染函数是先执行循环,在看条件判断,如果将v-if和v-for写在一个标签内,哪怕只渲染列表中的一小部分,也要重新遍历整个列表,无形造成资源浪费。vu…...
.)
Mapstruct 常用案例(持续更新.).
将A转换为B Mapper(componentModel "spring") public interface DemoConvert {B A2B(A a); }将List转换为List 注意:以下两个都不可缺少,需要先声明单个和集合的同时生命才可 Mapper(componentModel "spring") public interface …...
QT5网络与通信)
QT基础篇(10)QT5网络与通信
QT5网络与通信是指在QT5开发环境中使用网络进行数据传输和通信的相关功能和技术。 QT5提供了一套完善的网络模块,包括了TCP、UDP、HTTP等协议的支持,可以方便地在QT应用程序中进行网络通信。通过QT5的网络模块,开发者可以实现客户端和服务器…...
)
【Leetcode】269.火星词典(Hard)
一、题目 1、题目描述 现有一种使用英语字母的火星语言,这门语言的字母顺序与英语顺序不同。 给你一个字符串列表 words ,作为这门语言的词典,words 中的字符串已经 按这门新语言的字母顺序进行了排序 。 请你根据该词典还原出此语言中已知的字母顺序,并 按字母递增顺序…...

opencv_模型训练
文件夹 opencv训练文件 xml negdataposdata 说明 negdata目录: 放负样本的目录 posdata目录: 放正样本的目录 xml目录: 新建的一个目录,为之后存放分类器文件使用 neg.txt: 负样本路径列表 pos.txt: 正样本路径列表 pos.vec: 后续自动生成…...
python PyQt5的学习
一、安装与配置 1、环境: python3.7 2、相关模块 pip install pyqt5 pyqt5-tools pyqt5designer 可以加个镜像 -i https://pypi.tuna.tsinghua.edu.cn/simple3、配置设计器 python的pyqt5提供了一个设计器,便于ui的设计 界面是这样的:…...

3.goLand基础语法
目录 概述语法for常量与变量数组切片 slice切片问题问题1问题2 Make 和 New结构体和指针结构体标签 结束 概述 从 java 转来学 go ,在此记录,方便以后翻阅。 语法 for package mainimport "fmt"func main() {for i : 0; i < 3; i {fmt.…...
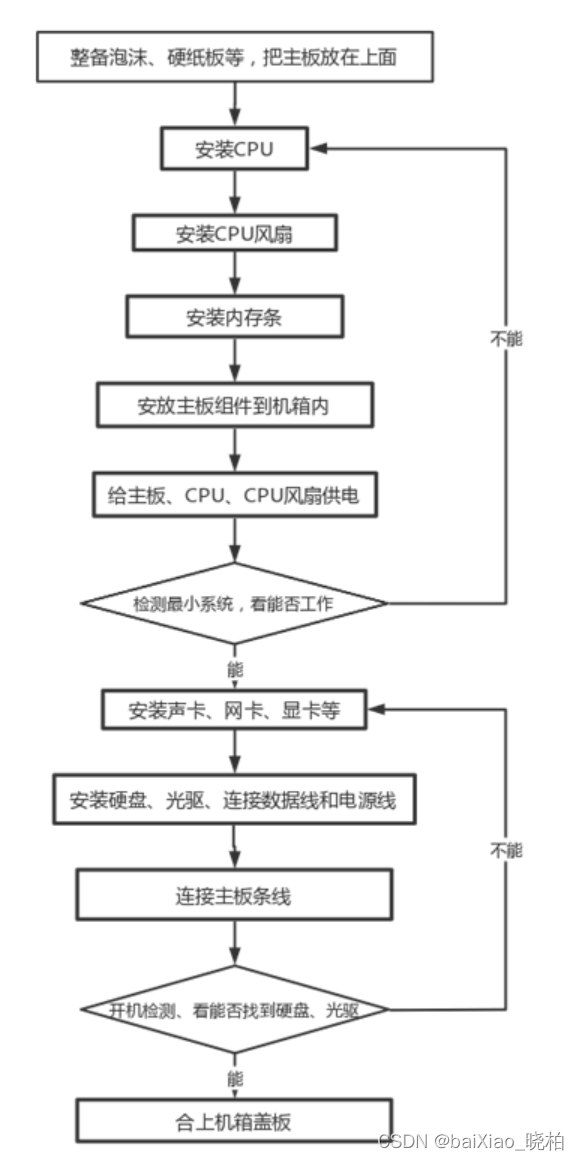
计算机硬件 5.2组装整机
第二节 组装整机 一、准备工作 1.常用工具:中号十字螺丝刀、尖嘴钳、软毛刷、防静电手环等。 2.组装原则: ①按“先小后大”“从里到外”的顺序进行,不遗漏每一环节,不“带病”进行下一环节。 ②合理使用工具器材,…...
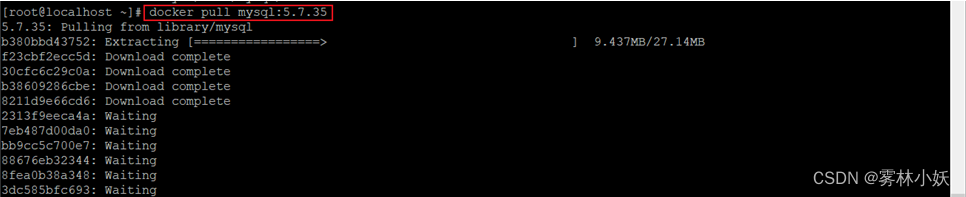
Docker搭建MySQL主从数据库-亲测有效
1、测试环境概述 1、使用MySQL5.7.35版本 2、使用Centos7操作系统 3、使用Docker20版本 案例中描述了整个测试的详细过程 2、安装Docker 2.1、如果已经安装docker,可以先卸载 yum remove -y docker \ docker-client \ docker-client-latest \ docker-common \ docker-l…...
PyTorch 中的距离函数深度解析:掌握向量间的距离和相似度计算
目录 Pytorch中Distance functions详解 pairwise_distance 用途 用法 参数 数学理论公式 示例代码 cosine_similarity 用途 用法 参数 数学理论 示例代码 输出结果 pdist 用途 用法 参数 数学理论 示例代码 总结 Pytorch中Distance functions详解 pair…...

【Vue技巧】vue3中不支持.sync语法糖的解决方案
海鲸AI-ChatGPT4.0国内站点,支持设计稿转代码:https://www.atalk-ai.com 在 Vue 3 中,.sync 修饰符已经被移除。在 Vue 2 中,.sync 修饰符是一个语法糖,用于简化子组件和父组件之间的双向数据绑定。在 Vue 3 中&#x…...

设计模式⑦ :简单化
文章目录 一、前言二、Facade 模式1. 介绍2. 应用3. 总结 三、Mediator 模式1. 介绍2. 应用3. 总结 一、前言 有时候不想动脑子,就懒得看源码又不像浪费时间所以会看看书,但是又记不住,所以决定开始写"抄书"系列。本系列大部分内容…...
Java:选择哪个Java IDE好?
Java:选择哪个Java IDE好? 在开始前我有一些资料,是我根据网友给的问题精心整理了一份「java的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!&…...

unity打包apk后网络请求提示unknown error处理
近期同事的一个比较老的版本的unity项目在电脑上运行都正常,但是打包成android后安装到手机上就提示unknown error 让我帮他排查一下问题。由于是涉密项目不能发图就简单介绍下处理过程吧! 一、故障原因 请求的地址ssl证书过期了。 二、处理过程 更改请…...
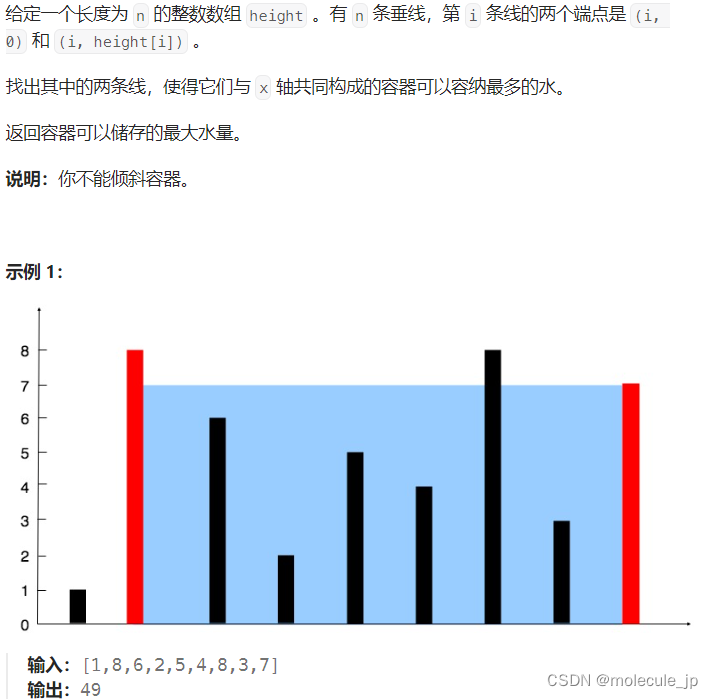
力扣 | 11. 盛最多水的容器
双指针解法–对撞指针 暴力解法public int maxArea1(int[] height) {int n height.length;int ans 0;for (int i 0; i < n; i) {for (int j i 1; j < n; j) {int area Math.min(height[i], height[j]) * (j - i);ans Math.max(ans, area);}}return ans;}双指针解法…...

史上最全EasyExcel
一、EasyExcel介绍 1、数据导入:减轻录入工作量 2、数据导出:统计信息归档 3、数据传输:异构系统之间数据传输 二、EasyExcel特点 Java领域解析、生成Excel比较有名的框架有Apache poi、jxl等。但他们都存在一个严重的问题就是非常的耗内…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
