算法笔记(动态规划入门题)
1.找零钱

int coinChange(int* coins, int coinsSize, int amount) {int dp[amount + 1];memset(dp,-1,sizeof(dp));dp[0] = 0;for (int i = 1; i <= amount; i++)for (int j = 0; j < coinsSize; j++)if (coins[j] <= i && dp[i - coins[j]] != -1)if (dp[i] == -1 || dp[i] > dp[i - coins[j]] + 1)dp[i] = dp[i - coins[j]] + 1;return dp[amount];
}2.有奖问答

#include <iostream>
using namespace std;
int ans=0;
int dp[31][10];//dp[i][j]代表回答了i道题目时得到了j*10的分数的 总方案数
int main(){dp[0][0] = 1;//初始化起点,起点就表示一个方案数for(int i = 1;i<=30;i++)for(int j = 0;j<=9;j++)if(j==0)//得到零分,说明这一题答错了,那么方案数量就是上一题的所有方案之和,上一题多少分都不影响当前题,因为一旦答错,分数归零。for(int k = 0;k<=9;k++)dp[i][j] += dp[i-1][k];else//答对了,那么说明这个方案必须承接上一次答对的方案数,上一题必须是当前分数-10,即j-1道题。dp[i][j] = dp[i-1][j-1];for(int i = 0;i<=30;i++)ans+=dp[i][7];//记录所有答对7次的方案数cout<<ans;return 0;answerquest
}3.字符串转换

#include <iostream>
#include <cstdio>
#include <string>
using namespace std;
string s,t;
int transform(){int l1=s.length(),l2=t.length();int dp[l1+1][l2+1];for(int i=0;i<l1;i++)dp[i][0]=i;for(int j=0;j<l2;j++)dp[0][j]=j;for(int i=1;i<=l1;i++)for(int j=1;j<=l2;j++){if(s[i-1]==t[j-1])dp[i][j]=dp[i-1][j-1];elsedp[i][j]=min(min(dp[i][j-1],dp[i-1][j]),dp[i-1][j-1])+1;}return dp[l1][l2];
}
int main()
{// 请在此输入您的代码cin>>s>>t;printf("%d",transform());return 0;
}动态规划浅析——记一道困难的字符串操作数问题 - 知乎 (zhihu.com)这个文章写的很不错,可以看看。
4.完全背包问题

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int n,v;
struct obj{int v;//体积int c;//价值
};
int packet(obj o[]){int dp[n+1][v+1];//选第i个物品且体积为j时的价值memset(dp,0,sizeof(dp));for(int i=1;i<=n;i++){for(int j=0;j<=v;j++){dp[i][j]=dp[i-1][j];for(int k=0;k*o[i].v<=j;k++){dp[i][j]=max(dp[i][j],dp[i-1][j-k*o[i].v]+k*o[i].c);}}}return dp[n][v];
}
int main()
{// 请在此输入您的代码scanf("%d%d",&n,&v);obj o[n+1];o[0].v=0,o[0].c=0;for(int i=1;i<=n;i++)scanf("%d%d",&o[i].v,&o[i].c);printf("%d",packet(o));return 0;
}5.松散子序列

#include <iostream>
#include <string>
#include <cstring>
using namespace std;
string s;
inline int value(char a){return a-'a'+1;
}
int SubSeq(){int len=s.length();int dp[len];memset(dp,0,sizeof(dp));dp[0]=value(s[0]);dp[1]=max(dp[0],value(s[1]));for(int i=2;i<len;i++)dp[i]=max(dp[i-1],dp[i-2]+value(s[i]));return dp[len-1];
}
int main()
{// 请在此输入您的代码cin>>s;cout<<SubSeq();return 0;
}
//字符串版的打家劫舍,挺简单的————部分代码是别人写的题解,本人仅为转载,非原创;
相关文章:

算法笔记(动态规划入门题)
1.找零钱 int coinChange(int* coins, int coinsSize, int amount) {int dp[amount 1];memset(dp,-1,sizeof(dp));dp[0] 0;for (int i 1; i < amount; i)for (int j 0; j < coinsSize; j)if (coins[j] < i && dp[i - coins[j]] ! -1)if (dp[i] -1 || dp[…...

开发实践_阶段三
编写一个告知APP。 需求: 1.登录、注册 2.发布定向讯息:检测是否登录,是则向用户或用户组发布 ”名称 时间“ ;否则提示登录 3.讯息接收:检测是否登录,是则查看收到信息(未读数)…...

codegeex和通义灵码辅助编程——以及通义灵码无法登陆的bug解决
通义的速度更快,延迟低,150ms。 codegeex速度慢些,延迟较高,500ms。 个人评价:延迟低的会很好地改善使用体验,所以通义加分。 但是整体功能上还是codegeex强一些,可以选中代码进行对话…...

Android14之DefaultKeyedVector实现(一百八十二)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...
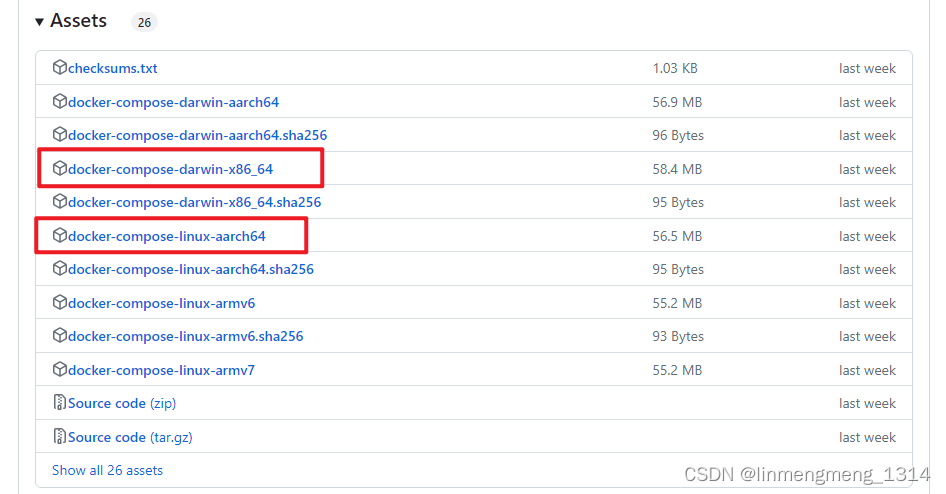
银河麒麟操作系统 v10 中离线安装 Docker
银河麒麟操作系统 v10 中离线安装 Docker 1. 查看系统版本2. 查看 Linux 内核版本(3.10以上)3. 查看 iptabls 版本(1.4以上)4. 判断处理器架构5. 离线下载 Docker 安装包6. 移动解压出来的二进制文件到 /usr/bin 目录中7. 配置 Do…...

如何系统的学习Python
学习 Python 的时候,可以按照以下步骤进行系统学习: 学习 Python 基础知识:首先了解 Python 的基础语法、数据类型、变量和运算符等基本概念。可以通过阅读《Python编程从入门到实践》等经典教材来建立基础。也可以通过翻阅Python官方文档来进…...

Java并发基础:一文讲清util.concurrent包的作用
java.util.concurrent包是 Java 中用于并发编程的重要工具集,提供了线程池、原子变量、并发集合、同步工具类、阻塞队列等一系列高级并发工具类,使用这些工具类可以极大地简化并发编程的难度,减少出错的可能性,提高程序的效率和可…...

C++PythonC# 三语言OpenCV从零开发(2):教程选择
文章目录 相关专栏前言视频教学和官方文档视频教程OpenCV 官方教程最终选择我的最终选择 相关专栏 C&Python&Csharp in OpenCV 前言 OpenCV 有官方的教程和简单的视频教程: OpenCV 官方教程 B站也有相关的视频教学 OpenCV4 C 快速入门视频30讲 - 系列合集 …...

【嘉立创EDA-PCB设计指南】3.网络表概念解读+板框绘制
前言:本文对网络表概念解读板框绘制(确定PCB板子轮廓) 网络表概念解读 在本专栏的上一篇文章【嘉立创EDA-PCB设计指南】2,将设计的原理图转为了PCB,在PCB界面下出现了所有的封装,以及所有的飞线属性&…...
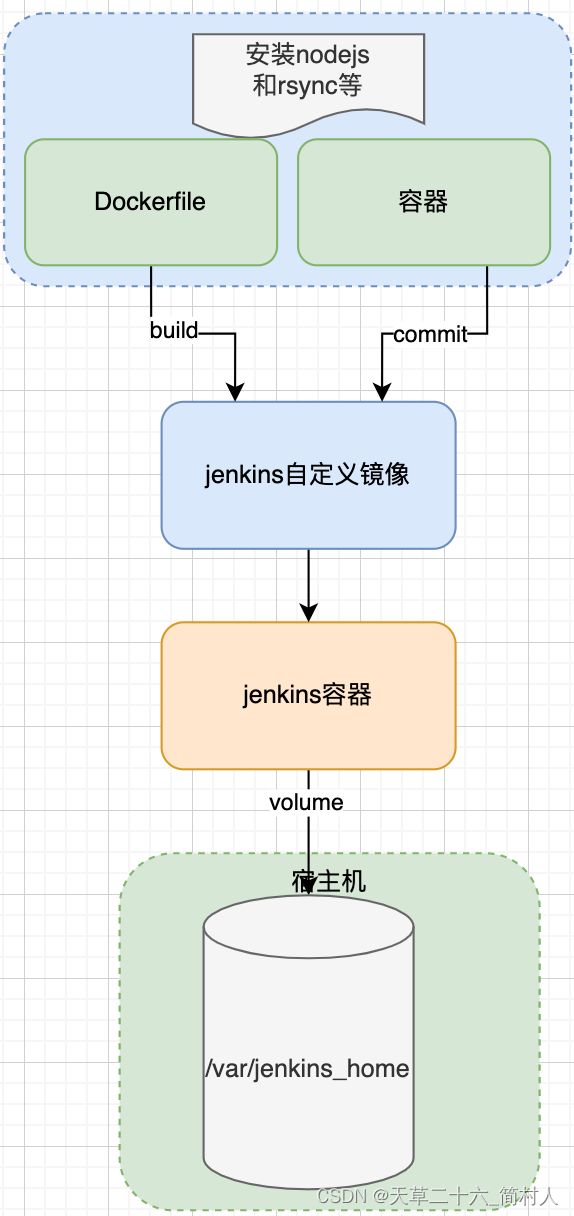
nodejs前端项目的CI/CD实现(二)jenkins的容器化部署
一、背景 docker安装jenkins,可能你会反问,这太简单了,有什么好讲的。 我最近就接手了一个打包项目,它是一个nodejs的前端项目,jenkins已在容器里部署且运行OK。 但是,前端组很追求新技术,不…...

python爬虫案例分享
当然,我可以分享一个基本的Python爬虫示例。这个示例将使用Python的requests库来抓取网页内容,然后使用BeautifulSoup库来解析和提取信息。我们将构建一个简单的爬虫来从一个示例网站抓取标题。 Python爬虫示例 目标 提取某网站的标题。 需要的库 r…...

【CC++】为什么 scanf 函数在读取字符串时不需要用取地址运算符
在C语言中如何使用 scanf 读取字符串 在C语言中,字符串实际上是字符数组,所以我们可以使用scanf函数来读取字符串。但是,需要注意的是,scanf在读取字符串时会在遇到空格、制表符或换行符时停止。因此,它不能用于读取包…...
)
Linux dirs命令教程:dirs命令详解与实例(附实例详解和注意事项)
Linux dirs命令介绍 dirs这是一个内置在shell中的命令,用于显示当前被记忆的目录列表。默认状态下,它会按照stack的方式储存目录,即最后加入的目录会被首先列出来。 Linux dirs命令适用的Linux版本 dirs命令在所有常见的Linux发行版中都适…...
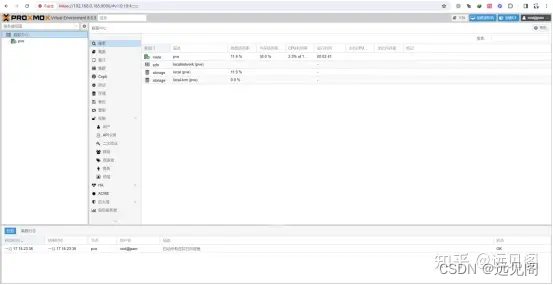
掌握虚拟化:PVE平台安装教程与技术解析
🌟🌌 欢迎来到知识与创意的殿堂 — 远见阁小民的世界!🚀 🌟🧭 在这里,我们一起探索技术的奥秘,一起在知识的海洋中遨游。 🌟🧭 在这里,每个错误都…...

Godot FileDialog无法访问其它盘符的文件
问题描述 使用Godot的FileDialog对象访问Windows系统的文件,例如: func _on_hud_sig_save():var dlg FileDialog.new()dlg.set_access(FileDialog.ACCESS_FILESYSTEM)dlg.set_file_mode(FileDialog.FILE_MODE_SAVE_FILE)add_child(dlg)dlg.popup_cent…...

TestNG注释
目录 TestNG注释列表 BeforeXXX和AfterXXX注释放在超类上时如何工作? 使用BeforeXXX和AfterXXX TestNG注释 TestNG是一个测试框架,旨在简化广泛的测试需求,从单元测试(隔离测试一个类)到集成测试(测试由…...

数据预处理 matlab 数据质量评估
知乎 数据类型转换等 Mathworks 数据预处理 概念辨析 配对是同一批样本的前后比较,独立是两批不同样本的的比较 独立样本是指我们得到的样本是相互独立的。配对样本就是一个样本中的数据与另一个样本中的数据相对应的两个样本。配对样本可以消除由于样本指定的不公…...
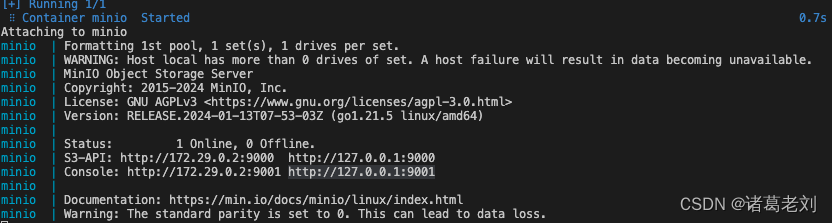
对象存储, 开源MinIO docker-compose.yml 文件
文章目录 python SDK 文档地址:docker-compose.yml 文件控制台使用:应用服务中使用样例: python SDK 文档地址: https://min.io/docs/minio/linux/developers/python/API.html docker-compose.yml 文件 version: 3services:min…...
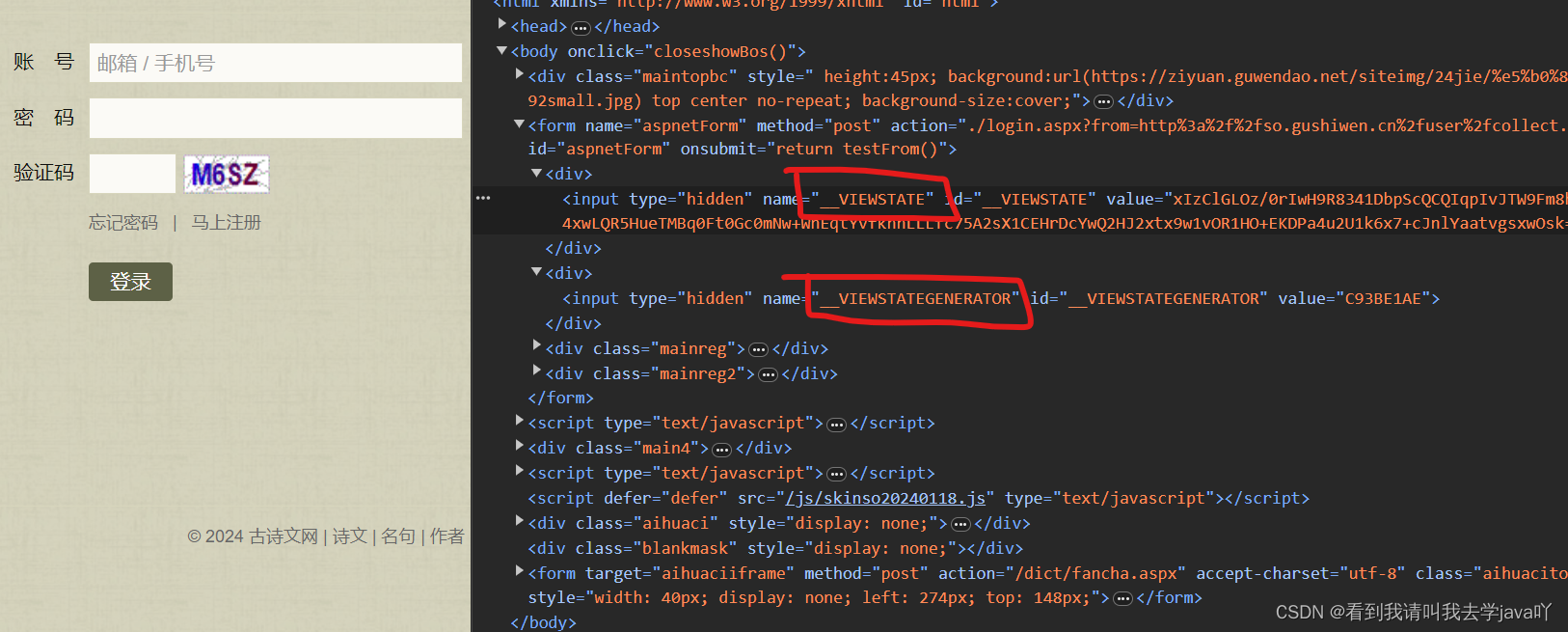
爬虫笔记(一):实战登录古诗文网站
需求:登录古诗文网站,账号+密码+图形验证码 第一:自己注册一个账号+密码哈 第二:图形验证码,需要一个打码平台(充钱,超能力power!)或…...
适用于 Windows 11 的 12 个最佳免费 PDF 编辑器
除了绘图等基本功能外,一些适用于 Windows 11 的免费 PDF 编辑器还具有 AI、OCR 识别和书签等高级功能。 我们的列表包含易于立即下载的 PDF 编辑软件工具。 这些工具不仅可以帮助转换 PDF、编辑、上传、删除、裁剪、分割、提取等。 PDF 是指便携式文档格式&…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
